中红外光谱双重校验异常样本检测方法研究

引用本文

张朱珊莹, 张若静, 顾瀚文, 谢勤岚, 张献文, 撒继铭, 刘繄. 中红外光谱双重校验异常样本检测方法研究[J]. 光谱学与光谱分析, 2024,44(6): 1546-1552.
ZHANGZHU Shan-ying, ZHANG Ruo-jing, GU Han-wen, XIE Qin-lan, ZHANG Xian-wen, SA Ji-ming, LIU Yi. Research on the Twin Check Abnormal Sample Detection Method of Mid-Infrared Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2024,44(6): 1546-1552.
Doi:10.3964/j.issn.1000-0593(2024)06-1546-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

中红外光谱双重校验异常样本检测方法研究

张朱珊莹^1,^2,³, 张若静^1,^2,³, 顾瀚文⁵, 谢勤岚^1,^2,^3,^*, 张献文^4,^*, 撒继铭⁵, 刘繄^6,³

1. 中南民族大学生物医学工程学院, 湖北武汉 430074

2. 认知科学国家民委重点实验室, 湖北武汉 430074

3. 医学信息分析及肿瘤诊疗湖北省重点实验室, 湖北武汉 430074

4. 临沂格莱普园林机械有限公司, 山东临沂 276700

5. 武汉理工大学信息工程学院, 湖北武汉 430070

6. 武汉理工大学机电工程学院, 湖北武汉 430070

*通讯作者 e-mail: xieqinlan@126.com; zxwen84@163.com

作者简介: 张朱珊莹, 女, 1982年生, 中南民族大学生物医学工程学院讲师 e-mail: syzhu@mail.scuec.edu.cn

收稿日期: 2023-05-31 修回日期: 2023-09-25

基金: 国家自然科学基金项目(61501526, 61178087)资助

摘要

中红外吸收光谱法目前最有前途的无创血糖检测技术之一。中红外吸收光谱的血糖浓度检测结果准确性与光谱信号的可靠性密切相关。采集中红外光谱信号的过程易受环境或人为等因素的影响而产生包含大量干扰信息的异常光谱。异常样本存在会降低预测模型的有效性和可靠性, 故异常样本的检测和剔除至关重要。本研究提出双重校验异常样本检测法能够将异常样本准确筛选出来并剔除。本算法分为两个阶段, 首先利用蒙特卡洛交叉验证异常样本检测, 初步筛选异常样本, 提高光谱样本集的稳定性; 其次以马氏距离平方近似服从卡方分布为理论基础, 自适应确定最优阈值, 对剩余数据集进行异常样本再识别。以64份包含葡萄糖、白蛋白、尿素、乳酸、果糖、胆固醇在内的葡萄糖混合仿体溶液样本为研究对象。双重校验法首先利用预测误差平方和对异常样本敏感的特性对光谱数据集中的异常样本进行初步判定, 共检测出3个异常样本, 从光谱数据集中剔除检测出的异常样本后建立PLS校正模型, 该模型的相关系数为0.91, RMSECV为60.17 mg·dL^-1。其次, 双重校验法以马氏距离平方近似服从卡方分布为理论基础, 实现异常样本自适应识别。共检测出了12个异常样本, 剔除全部异常样本后构建的PLS模型性能得到了提升, 相关系数达到0.99, RMSECV达到57.77 mg·dL^-1。通过与无异常样本剔除、 PCA-MD法、蒙特卡洛法相比较双重校验法结果最优, 证明了本算法在异常样本检测上的优越性。与未剔除异常样本时的PLS模型相比, 相关系数从0.86上升到了0.99, RMSECV从67.51 mg·dL^-1降低至57.77 mg·dL^-1, 分别提升了15.12%、 14.42%。本研究针对异常样本检测方法中易受阈值影响而出现正常样本误检或异常样本漏检的问题给出了很好的解决策略, 该方法能够准确检测并剔除异常样本, 进而提高预测模型的精度和预测性能。为中红外光谱数据集异常样本的准确剔除提供了一种思路。

关键词: 红外光谱; 异常样本; 双重校验; 自适应阈值

中图分类号:O433.1 文献标志码:A

Research on the Twin Check Abnormal Sample Detection Method of Mid-Infrared Spectroscopy

ZHANGZHU Shan-ying^1,^2,³, ZHANG Ruo-jing^1,^2,³, GU Han-wen⁵, XIE Qin-lan^1,^2,^3,^*, ZHANG Xian-wen^4,^*, SA Ji-ming⁵, LIU Yi^6,³

1. College of Biomedical Engineering, South-Central Minzu University, Wuhan 430074, China

2. Key Laboratory of Cognitive Science, State Ethnic Affairs Commission, Wuhan 430074, China

3. Hubei Key Laboratory of Medical Information Analysis and Tumor Diagnosis & Treatment, Wuhan 430074, China

4. Linyi Grepo Garden Machinery Co., Ltd., Linyi 276700, China

5. School of Information Engineering, Wuhan University of Technology, Wuhan 430070, China

6. School of Mechanical and Electrical Engineering, Wuhan University of Technology, Wuhan 430070, China

*Corresponding authors

Abstract

Mid-infrared absorption spectroscopy is one of the most promising non-invasive blood glucose measurement techniques. The accuracy of blood glucose concentration measurement results of the mid-infrared absorption spectrum is closely related to the reliability of spectral signals. However, collecting mid-infrared spectral signals is susceptible to environmental or human factors, and an anomaly spectrum containing a large amount of interference information will be generated. The existence of an anomaly spectrum will reduce the effectiveness and reliability of the prediction model, so the detection and removal of abnormal samples are crucial. This study proposes that the twin check abnormal sample detection method can accurately screen and eliminate abnormal samples. This algorithm is divided into two stages. Firstly, the Monte Carlo cross-validation abnormal sample detection method is used to preliminarily screen abnormal samples and improve the stability of the spectral sample set. Secondly, based on the theory that Mahalanobis distance square approximately obeys chi-square distribution, the optimal threshold is adaptively determined, and the remaining data sets are re-identified with abnormal samples. 64 samples of the glucose-mixed imitated solution containing glucose, albumin, urea, lactic acid, fructose and cholesterol were studied. The twin check method first uses the characteristic that the sum of squared prediction errors is sensitive to abnormal samples to make a preliminary judgment on the abnormal samples in the spectral data set, and a total of 3 abnormal samples are detected. The PLS correction model is established after removing the abnormal samples from the spectral data set. The correlation coefficient of this model is 0.91, and RMSECV is 60.17 mg·dL^-1. Secondly, the twin check method is based on the theory of Mahalanobis distance square approximately conforming to chi-square distribution, which realizes the adaptive identification of abnormal samples. A total of 12 abnormal samples were detected. The performance of the PLS model constructed after removing all abnormal samples was improved, with the correlation coefficient reaching 0.99 and RMSECV reaching 57.77 mg·dL^-1. By comparing the results of the twin check method with the non-abnormal sample removal, PCA-MD method and Monte Carlo method, the superiority of this algorithm in abnormal sample detection is proved. Compared with the PLS model without removing abnormal samples, the correlation coefficient increased from 0.86 to 0.99, and RMSECV decreased from 67.51 to 57.77 mg·dL^-1, increasing by 15.12% and 14.42%, respectively. This study provides a good solution strategy for the problem of false detection of normal samples or missing detection of abnormal samples due to the easy influence of threshold of existing abnormal sample detection methods, which is conducive to the method's accurate detection and elimination of abnormal samples, thus improving the accuracy and prediction performance of the prediction model. This method provides a way to eliminate the abnormal samples of mid-infrared absorption spectrum accurately.

Keyword: Infrared spectroscopy; Abnormal sample; Twin check; Adaptive threshold

文章图片

引言

中红外吸收光谱因其具有葡萄糖指纹吸收区能够实现葡萄糖的定量分析而被认为是无创血糖检测领域最有前途的技术之一^[1]。由于背景干扰、分子基团多样性导致的光谱谱峰重叠等因素, 使基于中红外光谱技术的血糖检测在临床应用上存在较大的误差与困难。目前具有高准确度的中红外无创血糖检测仪器尚不存在。

基于中红外吸收光谱血糖检测结果的准确性与光谱信号的可靠性密切相关, 故甄别所测得的光谱信号, 剔除异常样本, 能够提高校正模型关联有效样本信息的能力, 从而构建稳健的校正模型^[2], 并提高检测准确度。目前异常样本检测已存在多种经典检测方法, 如马氏距离法、杠杆值与学生化残差法以及光谱残差法等, 初步满足了剔除异常样本的需求^{[3, 4]}。为了更准确地识别异常样本, 许多学者采用稳健回归估计避免异常样本对校正模型稳定性的影响, 提高了多元校正模型的准确性^[5]。然而, 掩蔽效应可能会导致异常样本检测方法发生误检或漏检问题, 即异常样本的检测失败或者正常样本被错误识别为异常样本^{[6, 7]}。因此有研究借鉴了模型集成思想, 利用蒙特卡洛交叉验证建立一系列模型, 考虑异常样本在正常校正模型与异常校正模型中的不同分布, 提出了基于蒙特卡洛交叉验证的异常样本检测方法(Monte Carlo cross validation, MCCV), 降低了掩蔽效应的风险^{[7, 8]}。 Jiang等利用多元校正模型对异常样本的敏感性这一特性, 结合蒙特卡洛采样方法建立大量模型, 利用预测误差平方和对异常样本的响应机制检测异常样本^[9]。研究结果表明, 预测误差平方和更大的校正模型中存在异常样本的概率更高, 相比于基于留一交叉验证的异常样本检测^[10], 具有较好的检测异常样本的能力。

相比于经典异常样本检测与基于稳健回归估计的异常样本检测方法, 蒙特卡洛交叉验证异常样本检测法对异常样本的识别准确性更高, 是一种更为有效的异常样本检测方法。然而, 该异常样本检测方法引入了随机性, 使得在迭代次数较低的时候难以保证异常样本检测结果的准确性与稳定性。此外, 异常样本检测方法的关键在于判定阈值的合理设置, 通常选择大于阈值的样本作为异常样本。虽然每种异常样本检测方法自身具有相应的阈值选择策略, 但不同光谱数据集的特性不同, 使得处于阈值附近的样本可能存在误检现象, 降低了异常样本检测方法的可靠性。

本研究提出了双重校验异常样本检测法, 首先采用蒙特卡洛交叉验证异常样本检测方法解决稳健性较低的问题, 然后针对主流异常样本检测方法的阈值易受人为因素影响, 通过采用卡方分布实现异常样本最优阈值自适应。并与不同异常样本检测方法相比较, 证明了该方法在异常样本检测上的优越性。

1 实验部分

1.1 数据集

1.1.1 样本制备

在文献[11, 12]的基础上, 采用母液配制法制备了64份包含葡萄糖、白蛋白、尿素、乳酸、果糖、胆固醇在内的葡萄糖混合仿体溶液样本, 各组分的浓度范围及浓度梯度如表1所示。为确保仿体溶液样本的代表性以及小样本实验的鲁棒性, 所有仿体溶液样本中各分析物的浓度大小利用Minitab依据因子设计进行随机分配。制备的葡萄糖仿体溶液样本共包含13个葡萄糖浓度, 每个浓度之间相差20 mg· dL^-1, 其他成分的浓度范围如表1所示。

表1 各组分浓度范围及浓度梯度 Table 1 Concentration range of each component and concentration gradient

1.1.2 光谱测量

采用Bruker公司的INVENIO-R光谱仪对不同葡萄糖浓度的仿体溶液样本进行中红外光谱数据采集, 测量方式为衰减全反射。光谱采集范围为4 500~400 cm^-1, 扫描16次后取平均值, 分辨率为2 cm^-1。

64个葡萄糖仿体溶液样本中红外吸收光谱图如图1(a)所示。从图1(a)中能够看出, 890~400 cm^-1之间存在大量的光谱噪声和仪器噪声。将该光谱区间从原始光谱信号中去除, 采用4 500~890 cm^-1范围内的光谱信号进行分析与研究, 如图1(b)所示。

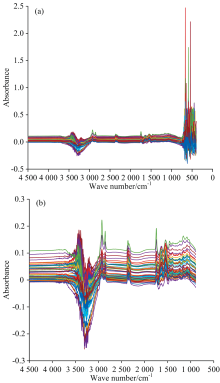	Figure Option View Download New Window
	图1 (a) 全波段吸收光谱图; (b) 4 500~890 cm^-1吸收光谱图 1.2 算法原理 1.2.1 主成分分析-马氏距离异常样本检测Fig.1 (a) Full-band absorption spectra; (b) 4 500~890 cm^-1absorption spectra

马氏距离法(Mahalanobis distance, MD)是较为常用的异常样本检测方法^[13], 衡量了样品光谱与平均光谱之间的相似度, 相似度较低的样本被识别为异常样本。通常利用主成分分析(principal component analysis, PCA)压缩光谱矩阵, 将高维光谱信号映射至低维正交子空间中, 降低光谱信号维数, 构建有效的协方差矩阵。因此将PCA与马氏距离法相结合可以提高马氏距离的稳定性, 降低误检或漏检发生的概率。

1.2.2 蒙特卡洛交叉验证异常样本检测

该异常样本检测方法会对所测得的光谱数据集进行多次随机划分, 构建大量互不相同的多元校正模型, 利用异常样本与正常样本在校正模型性能表达上的差异性检测异常样本。当校正集包含异常样本时, 降低了多元校正模型的预测性能, 使测试集样本的误差平方和整体较大; 当异常样本出现在测试集上时, 多元校正模型具有正常的预测性能, 测试集中只有异常样本的误差平方和较大。预测误差的敏感性能够在一定程度上降低掩蔽效应的危害, 使得基于蒙特卡洛交叉验证的异常样本具有较优的异常样本检测能力。该异常检测方法的原理^[14]:

(1)在全部光谱数据集上建立偏最小二乘模型, 依据交叉验证均方根误差(root mean square error of cross validation, RMSECV)确定PLS模型的最佳主成分ncomp。 RMSECV的具体计算方式为

$RMSECV = \sqrt[]{\frac{1}{n - 1} \times (y - {\hat{y}}_{cv}) (y - {\hat{y}}_{cv})^{T}}$ (1)

式(1)中, y为校正集样本葡萄糖浓度的参比值, ${\hat{y}}_{cv}$ 为交叉验证过程中校正集样本葡萄糖浓度的预测值, n为校正集样本的样本数。

(2)从全部光谱数据集中使用蒙特卡洛采样每次随机选择一定比例的样本作为校正集, 其余的样本作为测试集。

(3)使用校正集建立PLS模型, 主成分数设置为ncomp。

(4)使用步骤(3)建立的多元校正模型计算测试集样品的误差。

(5)重复步骤(2)至步骤(4)K次, 确保每个样本在测试集中出现多次, 使得所有样本均存在一组误差向量residual。

(6)依据式(2)和式(3)计算每个样本预测误差向量的统计特征。

$μ_{i} = \frac{1}{J_{i}} \times \overset{J_{i}}{\sum_{j = 1}} residua l_{j}$ (2)

$σ_{i} = \sqrt[]{\frac{1}{J_{i} - 1} \times \overset{J_{i}}{\sum_{j = 1}} (residua l_{j} - μ_{i})}$ (3)

式(2)和式(3)中, μ _i为第i个样本误差向量的均值, σ _i为第i个样本误差向量的方差, J_i为第i个样本出现在测试集中的次数。

(7)按照式(4)和式(5)计算异常样品的阈值。

$T_{μ} = 2.5 \times μ_{mean} (μ_{mean} : 误差向量均值)$ (4)

$T_{σ} = 2.5 \times μ_{std} (μ_{std} : 误差向量方差)$ (5)

(8)选择样本误差均值大于T_μ, 同时样本误差方差大于T_σ的样本作为异常样本。

1.2.3 双重校验异常样本检测法

该异常样本检测方法包含两个阶段: 第一阶段利用MCCV法剔除远离阈值的样本, 完成对异常样本的初步筛选, 提升光谱数据集的总体稳定性; 在第二阶段, 以卡方分布为理论基础, 自适应确定最优阈值, 对剩余数据集进行异常样本再识别。文献[15]指出马氏距离的平方近似服从卡方分布。为了降低阈值选择的不确定性, 提高异常样本判别的准确性, 对阈值的选择策略进行改进, 借助卡方分布确定最优阈值的综合推导, 避免人为设定阈值导致误检或漏检, 实现光谱数据集中异常样本的自适应检测。双重校验算法的原理框图如图2所示, 每个阶段的主要步骤如下:

	Figure Option View Download New Window
	图2 双重校验异常样本检测法原理框图Fig.2 Principle block diagram of twin check abnormal sample detection method

(1)第一阶段

①利用蒙特卡洛异常样本检测方法识别原始数据集中的异常样本。

②从原始数据集中剔除步骤①中识别出的异常样本, 得到新的数据集Q_s。

(2)第二阶段

①在数据集Q_s上构建PLS校正模型, 计算相关系数(记为R), 计算公式为

$R = \sqrt[]{1 - \frac{(y - \hat{y}) {(y - \hat{y})}^{T}}{(y - \hat{y}) {(y - \hat{y})}^{T}}}$ (6)

式(6)中, y为校正集或者测试集样本葡萄糖浓度的参比值, $\hat{y}$ 为校正集样本或者测试集样本葡萄糖浓度的预测值, $\overset{̅}{y}$ 为校正集或者测试集所有样本葡萄糖浓度参比值的平均值。

②采用PCA对样本集Q_s进行降维, 得到压缩后的样本集 $Q_{s}^{*}$ 。

③计算数据集 $Q_{s}^{*}$ 中各光谱样本的马氏距离平方D²。

④搜索最优置信水平α _opt。

⑤通过α _opt确定阈值, 正常样本的识别区间通过椭圆区域确定, 表示为

$D^{2} \leq χ_{1 - α}^{2} = D_{Lim}^{2}$ (7)

式(7)中, $D_{Lim}^{2}$ 为马氏距离平方的判别限, 并且满足式(8)

$P \{χ^{2} = D^{2} \leq D_{Lim}^{2}\} = α$ (8)

⑥将马氏距离的平方大于阈值的样本判别为异常样本。

其中, 在第二阶段中搜索最优置信水平α _opt的步骤如下:

(1)从置信水平候选集V_α中随机选择一个置信水平α ^*。

(2)剔除α ^*对应阈值下识别出的异常样本后建立校正模型, 记为PLS_α。

(3)比较PLS_α与最优模型的性能以判断是否更新最优记录。

为了高效地实现最优记录的准确更新, 通过以下三种策略更新置信水平候选集、搜索最优置信水平, 从而确定最优阈值。

(1)策略一

若R_α> R_opt, 则引入高低水位置信水平以避免发生正常样本的误检。低水位置信水平与高水位置信水平分别表示为α _low与α _up, 且满足式(9)

$\{\begin{array}{l} α_{low} = α^{*} \\ α_{up} = {α \in V_{α} | α^{*} < α < \max (V_{α})} \end{array}$ (9)

从样本集 $Q_{s}^{*}$ 中剔除高低水位置信水平对应阈值之间的光谱样本, 构建双重校验样本集并建立PLS模型, 计算其相关系数 $R_{LU}^{2}$ 。

①若 $R_{LU}^{2}$ ≤ R, 则令V_α=V_α-{α |α < α _low}。

②若 $R_{LU}^{2}$ > R, 则令式(10)成立

$\{\begin{array}{l} R_{opt} = R_{α} \\ α_{opt} = α^{*} \\ V_{α} = V_{α} - {α | α > α_{up}} \end{array}$ (10)

(2)策略二

若R_α=R_opt, 则令式(11)成立

$\{\begin{array}{l} α_{opt} = \max \max (α_{opt}, α^{*}) \\ V_{α} = V_{α} - \{α| α = α^{*}\} \end{array}$ (11)

(3)策略三

若R_α< R_opt, 则最优置信水平以概率p更新, 则式(12)和式(13)成立

$α_{opt} = \{\begin{array}{l} α_{opt}, & p < random (0, 1) \\ α^{*}, & p < random (0, 1) \end{array}$ (12)

$R_{opt} = \{\begin{array}{l} R_{opt}, & p < random (0, 1) \\ R_{α}, & p < random (0, 1) \end{array}$ (13)

其中, 式(12)与式(13)中的概率的定义如式(14)

$p = e^{- N_{t} (R_{α}^{2} - R^{2})}, i = 1, 2, \dots, N$ (14)

式(14)中, N_i为第i次迭代次数, N为总迭代次数。

图3为策略一的原理示意图, 蓝色圆点代表正常样本, 粉色矩形点代表异常样本, 红色虚线代表阈值线, 位于阈值线上方的点代表双重校验法识别出的异常样本。策略一中搜索到更优的置信水平后, 通过该阈值所识别的异常样本中依然存在包含正常样本的可能性, 导致正常样本被错误识别为异常样本, 如图3中低阈值对应的情况。因而剔除高低水位置信水平对应阈值之间的样本, 构建PLS模型, 对识别出的异常样本进行双重校验。若存在误检样本, 则双重校验过程得到的 PLS 模型的性能较原 PLS 模型性能较差, 从置信水平候选集中移除小于低水位置信水平的值, 缩减解空间, 避免无效置信水平的搜索, 减少迭代次数, 提高最优置信水平搜索过程的收敛速度。

	Figure Option View Download New Window
	图3 策略一示意图Fig.3 The diagram of strategy one

观察式(9)— 式(13)可知, 在最优置信水平搜索过程的起始阶段, 较大的解空间以及随机性的引入有较大的概率发生低阈值现象如图3所示, 使得正常样本被错误识别为异常样本, 因此通过策略一避免低阈值现象的发生。同时, 在双重校验法的起始阶段对搜索过程中产生的较差置信水平采取一定的容忍度, 增强解空间的搜索范围, 避免陷入局部最优。随着迭代过程的推进, 异常样本检测结果趋于稳定, 其包含正常样本的概率逐渐降低, 最优阈值被更新为较差阈值的概率亦随之降低, 确保异常样本检测结果的准确性。

本方法利用快速选择思想控制候选集的收缩, 实现最优置信水平的更新。在随机选择α ^*后, 下一步是确定α ^*是否能够被接受以更新α _opt。分别构建α ^*与α _opt置信水平下的PLS模型, 计算其相关系数, 记为R_α与R_opt。若R_α更大, 则通过策略一进行双重校验避免正常样本的误检; 若R_opt更大, 则以概率p控制最优记录的更新; 若两者相同, α _opt被更新为更高的置信水平, 以降低被识别为异常样本的数量。直至候选集为空集, α _opt的搜索过程结束。

2 结果与讨论

实验使用SIMPLS算法构建PLS校正模型, 并采用留一交叉验证估计矫正模型的RMSECV。所有代码和计算均在Matlab R2019b中完成, CPU为Intel Core i5-10400F, RAM大小为16 GB。

2.1 双重校验法实验结果分析

双重校验法的第一阶段是对光谱数据集中的异常样本进行初步判定。第一阶段存在两个参数, 分别为采样比例和采样次数, 因此对该方法进行参数初始化: 采样比例设置为80%, 采样次数设置为1 000。以预测误差均值为横坐标、预测误差标准差为纵坐标画出各样本预测误差统计量的均值-方差图, 如图4所示。图4中虚线代表阈值线, 红点代表该阶段检测出的异常样本。从图4中能够看出, 33号、 49号、 62号样本的预测误差均值偏离阈值程度较为明显, 未发现预测误差标准差大于阈值的样本。由此可得, 双重校验法第一阶段共检测出的3个异常样本, 分别为33号、 49号、 62号样本。从光谱数据集中剔除第一阶段检测出的异常样本后建立PLS校正模型, 该模型的相关系数为0.91, RMSECV为60.17 mg· dL^-1。

	Figure Option View Download New Window
	图4 样本预测误差均值-方差图Fig.4 Mean-variance plot of sample prediction error

对剔除33号、 49号、 62号样本后的光谱数据集进行 PCA 降维, 以确定适合的主成分数量, 提取其映射数据后计算各光谱信号的马氏距离的平方。图5为各主成分方差贡献率Pareto图。从图5中能够看出, 第一主成分的方差贡献率为78.54%, 占有原光谱信息矩阵的绝大部分信息量, 其与第二、第三主成分累计方差贡献率共达到了99.31%, 表明前三个主成分占有原光谱信号的大部分信息量, 将其映射数据作为计算马氏距离平方的光谱数据。

	Figure Option View Download New Window
	图5 主成分方差贡献率Pareto图Fig.5 Principal component variance contribution rate Pareto plot

为了确定第二阶段异常样本判定的最优阈值, 最优置信水平的候选集的范围被设置为[68.3%∶ 0.1%∶ 99%]。图6与图7共同展示了该异常样本检测算法在迭代过程中候选集合随迭代次数变化而变化的情况。若在迭代过程中置信水平存在于候选集合, 则在图6中用圆点标记。图7的散点图代表候选集合的大小, 散点的拟合曲线用红色虚线表示。

	Figure Option View Download New Window
	图6 置信水平候选集元素随迭代次数变化曲线Fig.6 Confidence level candidate set elements curve withiteration times

	Figure Option View Download New Window
	图7 置信水平候选集大小随迭代次数变化曲线Fig.7 Confidence level candidate set size curve with iteration times

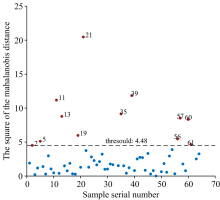
由图6图7知, 在迭代起始阶段, 最优置信水平的解空间较大, 策略一在保证最优阈值搜索准确性的同时快速剔除了置信水平候选集中的无效置信水平, 提高了双重校验法的收敛速度。随着迭代过程的推进, 无效置信水平的占比逐渐趋于零, 最优置信水平的搜索速度变缓, 确定的最优置信水平为78.6%, 得到双重校验法第二阶段的最优阈值为4.48, 得到异常检测结果如图8示, 其中虚线为阈值线, 异常样本被标识为红色。

	Figure Option View Download New Window
	图8 样本马氏距离平方散点图Fig.8 Sample Mahalanobis distance squared scatter plot

由图8知, 双重校验法在第二阶段共检测出了12个异常样本。结合该异常样本检测方法的两个阶段, 该异常样本检测算法共检测出15个异常样本。剔除全部的异常样本, 建立PLS校正模型以验证双重校验法的有效性, 得到校正模型的相关系数、 RMSECV值。并与无异常样本剔除、 PCA-MD法、蒙特卡洛法相比较, 如表2所示。

表2 剔除不同异常样本检测方法的识别结果后PLS模型性能指标 Table 2 The performance index of PLS model after eliminating the recognition results of different abnormal sample detection methods

表2可以得出, 双重校验法剔除全部异常样本后构建的PLS模型性能最优, 相关系数达到0.99, RMSECV达到57.77 mg· dL^-1。与未剔除异常样本时的PLS模型相比, 相关系数从0.86上升到了0.99, RMSECV从67.51 mg· dL^-1 降低至57.77 mg· dL^-1, 分别提升了15.12%、 14.42%。

3 结论

提出了异常样本双重校验法用来检测和剔除异常的光谱数据。利用该方法对64个葡萄糖混合仿体溶液进行异常样本的检测。首先, 利用蒙特卡洛交叉验证异常样本检测法, 初步筛选出3个异常样本。其次以马氏距离平方近似服从卡方分布为理论基础, 自适应确定最优阈值, 对剩余数据集进行异常样本再识别, 共检测出了12个异常样本, 完成异常样本的精细筛选。从原始光谱中剔除全部异常样本后构建 PLS 校正模型以验证双重校验法的有效性, 得到校正模型的相关系数为0.99、 RMSECV为57.77 mg· dL^-1。并与无异常样本剔除、 PCA-MD法、蒙特卡洛法相比较。研究结果表明, 双重检验异常样本检测法的有效性以及准确性更高, 剔除该方法识别出的异常样本后构建的校正模型性能最优。本研究为中红外光谱数据处理时异常样本的检测提供一种方法。

参考文献

文献列表

[1]	Marjan Gusev, Lidija Poposka, Gjoko Spasevski, et al. Journal of Sensors, 2020, 2020: 9628281. [本文引用:1]
[2]	Mekonnen B K, Yang W, Hsieh T H, et al. Biomedical Signal Processing and Control, 2020, 59: 101923 [本文引用:1]
[3]	Baba A M, Midi H, Adam M B, et al. Symmetry, 2021, 13(11): 2030. [本文引用:1]
[4]	ZHAO Zhi-lei, WANG Xue-mei, LIU Dong-dong, et al(赵志磊, 王雪妹, 刘冬冬, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(9): 2836. [本文引用:1]
[5]	LIAO Wen-hui, HUANG Ying-qiang, HE Zhi-feng, et al(廖文辉, 黄颖强, 何志锋, 等). Journal of Applied Statistics and Management(数理统计与管理), 2021, 40(5): 822. [本文引用:1]
[6]	CHEN Bo-wen, ZHUAN Sun-hao, JIN Yong-qi, et al(陈博文, 颛孙浩, 金咏琪, 等). Journal of Forest and Environment(森林与环境学报), 2022, 42(1): 88. [本文引用:1]
[7]	GUO Liang, LIU Jian-ya, LU Ruo-dan. Science China Mathematics, 2021, 64(1): 197. [本文引用:2]
[8]	ZHOU Yang, WANG Chun-lin, GUO Rui(周杨, 王春林, 郭锐). Modern Electronic Technology(现代电子技术), 2023, 46(8): 143. [本文引用:1]
[9]	JIANG Ming-wei, WANG Cai-hong, ZHANG Qing-hui(姜明伟, 王彩红, 张庆辉). Journal of Henan University of Technology(Natural Science Edition[河南工业大学学报(自然科学版)], 2020, 41(6): 91. [本文引用:1]
[10]	YUAN Ying, WANG Xue-feng(袁莹, 王雪峰). Scientia Silvae Sinicae(林业科学), 2022, 58(9): 36. [本文引用:1]
[11]	Ine L Jernelv, Karina Strom, Dag Roar Hjelme, et al. Sensors, 2019, 19(23): 5130. [本文引用:1]
[12]	Fuglerud S S, Ellingsen R, Aksnes A, et al. Journal of Biophotonics, 2021, 14(5): e202000450. [本文引用:1]
[13]	CHEN Ting, LIU Qing-jun, WU Yan-wen, et al(陈婷, 刘清珺, 武彦文, 等). Journal of Food Safety & Quality(食品安全质量检测学报), 2015, 6(3): 836. [本文引用:1]
[14]	SHI Lu-zhen, CHEN Jie, ZHANG Shu-yan, et al(石鲁珍, 陈杰, 张树艳, 等). Jiangsu Agricultural Sciences(江苏农业科学), 2018, 46(14): 205. [本文引用:1]
[15]	Etherington Thomas R. Peer J, 2019, 7: e6678. [本文引用:1]

2020

0.0

... 引言中红外吸收光谱因其具有葡萄糖指纹吸收区能够实现葡萄糖的定量分析而被认为是无创血糖检测领域最有前途的技术之一^[1] ...

2020

0.0

... 基于中红外吸收光谱血糖检测结果的准确性与光谱信号的可靠性密切相关, 故甄别所测得的光谱信号, 剔除异常样本, 能够提高校正模型关联有效样本信息的能力, 从而构建稳健的校正模型^[2], 并提高检测准确度 ...

2021

0.0

... 目前异常样本检测已存在多种经典检测方法, 如马氏距离法、杠杆值与学生化残差法以及光谱残差法等, 初步满足了剔除异常样本的需求^[3,4] ...

2022

0.0

... 目前异常样本检测已存在多种经典检测方法, 如马氏距离法、杠杆值与学生化残差法以及光谱残差法等, 初步满足了剔除异常样本的需求^[3,4] ...

2021

0.0

... 为了更准确地识别异常样本, 许多学者采用稳健回归估计避免异常样本对校正模型稳定性的影响, 提高了多元校正模型的准确性^[5] ...

2022

0.0

... 然而, 掩蔽效应可能会导致异常样本检测方法发生误检或漏检问题, 即异常样本的检测失败或者正常样本被错误识别为异常样本^[6,7] ...

2021

0.0

... 然而, 掩蔽效应可能会导致异常样本检测方法发生误检或漏检问题, 即异常样本的检测失败或者正常样本被错误识别为异常样本^[6,7] ...

... 因此有研究借鉴了模型集成思想, 利用蒙特卡洛交叉验证建立一系列模型, 考虑异常样本在正常校正模型与异常校正模型中的不同分布, 提出了基于蒙特卡洛交叉验证的异常样本检测方法(Monte Carlo cross validation, MCCV), 降低了掩蔽效应的风险^[7,8] ...

2023

0.0

2020

0.0

... Jiang等利用多元校正模型对异常样本的敏感性这一特性, 结合蒙特卡洛采样方法建立大量模型, 利用预测误差平方和对异常样本的响应机制检测异常样本^[9] ...

2022

0.0

... 研究结果表明, 预测误差平方和更大的校正模型中存在异常样本的概率更高, 相比于基于留一交叉验证的异常样本检测^[10], 具有较好的检测异常样本的能力 ...

2019

0.0

... 在文献[11,12]的基础上, 采用母液配制法制备了64份包含葡萄糖、白蛋白、尿素、乳酸、果糖、胆固醇在内的葡萄糖混合仿体溶液样本, 各组分的浓度范围及浓度梯度如表1所示 ...

2021

0.0

2015

0.0

... 马氏距离法(Mahalanobis distance, MD)是较为常用的异常样本检测方法^[13], 衡量了样品光谱与平均光谱之间的相似度, 相似度较低的样本被识别为异常样本 ...

2018

0.0

... 该异常检测方法的原理^[14]: ...

2019

0.0

... 文献[15]指出马氏距离的平方近似服从卡方分布 ...