引用本文
白宗璠, 韩玲, 姜旭海, 武春林. 微分光谱变换方法对土壤重金属含量反演精度的影响研究[J]. 光谱学与光谱分析, 2024,44(5): 1449-1456.
BAI Zong-fan, HAN Ling, JIANG Xu-hai, WU Chun-lin. Effect of Differential Spectral Transformation on Soil Heavy Metal Content Inversion Accuracy[J]. Spectroscopy and Spectral Analysis, 2024,44(5): 1449-1456.
Doi:10.3964/j.issn.1000-0593(2024)05-1449-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
微分光谱变换方法对土壤重金属含量反演精度的影响研究
白宗璠1, 韩玲1,*, 姜旭海1, 武春林2
1.长安大学土地工程学院, 陕西 西安 710075
2.西北有色地质矿业集团有限公司, 陕西 西安 710054
*通讯作者 e-mail: hanling@chd.edu.cn

作者简介: 白宗璠, 女, 1995年生, 长安大学土地工程学院博士研究生 e-mail: bzf1529@163.com

收稿日期: 2022-04-02 修订日期: 2023-08-31
基金: 国家科技重大专项(04-H30G01-9001-20/22), 国家自然科学基金项目(211035210511)资助
摘要

随着我国工农业的日益发展, 土壤中以镍(Ni)、 铁(Fe)、 铜(Cu)、 铬(Cr)、 铅(Pb)等为代表的重金属污染对人类生活产生了严重影响。 高光谱遥感技术具有实时、 无损、 快速等优点, 为高效准确地获取土壤重金属含量提供了科学手段。 而在利用高光谱数据反演土壤重金属含量时, 微分光谱变换方法的选择对遥感反演土壤重金属含量的精度有显著影响。 为明确二者关系, 基于研究区采集的60个土壤样品, 测定其Ni、 Fe、 Cr、 Cu、 Pb等含量以及350~2 500 nm波段范围的光谱反射率。 在相关系数(CC)分析法的基础上通过改进离散粒子群算法(MDBPSO)优选遥感探测土壤重金属含量的特征波段。 最终以优选出的特征波段作为自变量利用随机森林(RF)算法构建了Ni、 Fe、 Cr、 Cu、 Pb等重金属含量的估测模型。 在对原始反射率数据进行高斯平滑的基础上, 对比分析了一阶微分(R')、 对数倒数的一阶微分(1/lg R)'、 倒数的一阶微分(1/ R)'、 指数的一阶微分(eR)'四种微分光谱变换方法对土壤重金属反演精度的影响。 结果表明, 在CC分析法的基础上, MDBPSO算法可以有效地降低光谱数据的冗余度, 提高模型的运行效率。 其中 R'、 (1/lg R)'、 (1/ R)'、 (eR)'中对Ni、 Fe、 Cr、 Cu、 Pb敏感的特征波段个数分别至少减少了154、 363、 135、 744和889个。 (1/lg R)'、 R'、 R'、 (1/ R)'、 R'光谱变换方法分别应用到Ni、 Fe、 Cr、 Cu、 Pb特征波段的组合运算中, 得到的估测模型的精度优于其他微分变换方法; 模型检验集的决定系数分别为0.913、 0.906、 0.872、 0.912、 0.876, 均方根误差分别为0.743、 0.095、 2.588、 1.541、 1.453。 本研究为利用遥感数据反演土壤重金属含量微分光谱变换方法的选择提供了科学的参考, 为进一步实现土壤重金属含量的大面积高精度遥感监测提供新的思路。

关键词: 遥感; 高光谱; 土壤; 光谱变换方法; 重金属; 改进离散粒子群; 随机森林
中图分类号:TP79 文献标志码:A
Effect of Differential Spectral Transformation on Soil Heavy Metal Content Inversion Accuracy
BAI Zong-fan1, HAN Ling1,*, JIANG Xu-hai1, WU Chun-lin2
1. School of Land Engineering, Chang'an University, Xi'an 710075, China
2. Northwest Nonferrous Geological Mining Group Co., Ltd., Xi'an 710054, China
*Corresponding author
Abstract

With the increasing development of industry and agriculture in China, heavy metal pollution in soil represented by nickel (Ni), iron (Fe), copper (Cu), chromium (Cr), lead (Pb), etc., has a serious impact on human life. Hyperspectral technology has advantages such as being real-time, non-destructive, and fast, which provides scientific means to obtain information on soil heavy metal content efficiently and accurately. At the same time, the spectral transformation method significantly impacts the inversion accuracy of soil heavy metal content. To clarify the relationship between the spectral transformation method and the inversion accuracy, 60 soil samples were collected in the study area to determine the Ni, Fe, Cr, Cu, and Pb heavy metals content and the corresponding spectral reflectance between 350~2 500 nm. Based on the correlation coefficient (CC) analysis, the feature bands for remote sensing detection of soil heavy metals were selected by the modified discrete binary particle swarm optimization (MDBPSO) method. Finally, the inverse models of Ni, Fe, Cr, Cu and Pb contents were constructed by the random forest (RF) algorithm with the feature bands as independent variables. In this study, based on Gaussian smoothing of the original reflectance, the effects of four differential spectral transformation methods, including first-order differential (R'), first-order differential of logarithmic inverse (1/lg R)', first-order differential of inverse (1/ R)', and first-order differential of exponential (eR)', on the accuracy of soil heavy metal inversion were compared and analyzed. The results show that based on the CC analysis method, the MDBPSO algorithm can effectively reduce the redundancy of spectral data and improve the efficiency of the model operation. The number of feature bands sensitive to Ni, Fe, Cr, Cu and Pb in R', (1/lg R)', (1/ R)', (eR)', has been reduced by at least 154, 363, 135, 744 and 889, respectively. (1/lg R)', R', R', (1/ R)', and R' spectral transformation methods were applied to the combined operation of Ni, Fe, Cr, Cu, and Pb feature bands, respectively. The accuracy of the estimated models was better than other differential transformation methods, where the coefficients of determination of the model test set were 0.913, 0.906, 0.872, 0.912, and 0.876. The root mean square errors were 0.743, 0.095, 2.588, 1.541, and 1.453, respectively. This study provides a scientific reference for selecting of differential spectral transformation methods when using remote sensing data to retrieve soil heavy metal content. It provides new ideas for further realizing large-area high-precision remote sensing monitoring of soil heavy metal content.

Keyword: Remote sensing; Hyperspectral; Soil; Spectral transformation method; Heavy metals; Modified discrete binary particle swarm optimization; Random forests
引言

近年来随着工农业的发展, 土壤重金属造成的环境污染问题受到了广泛的关注。 土壤重金属的污染不仅对土壤的物理化学性质产生重要的影响, 还会抑制生物酶的活性[1, 2]。 因此, 实现土壤重金属含量的准确预测, 对治理土壤污染具有重要意义。 与传统的样品采集测定方法相比, 高光谱遥感技术具有实时、 无损、 快速等优点, 在获取土壤重金属污染信息中有着独特的优势[3]。 近年来, 利用高光谱遥感反演土壤重金属含量已经成为研究的重点, 并取得了丰硕的成果[4, 5, 6, 7, 8, 9]。 其中, 马驰等基于HJ-1A高光谱遥感影像, 利用反射率指数构建表层土壤游离氧化铁含量的反演模型可以很好的预测游离氧化铁的含量, 模型的决定系数为0.837[4]。 Liu等利用高光谱数据估算了土壤中砷, 镉和汞等重金属含量, 估算镉含量的相对均方根误差为17.41%[6]。

以上研究充分展示了高光谱数据反演土壤重金属含量的优势。 但是由于高光谱数据会受到背景、 噪声和环境等因素的影响, 所以在获取土壤高光谱数据后, 需要对其进行平滑去噪、 重采样、 光谱变换和光谱定量化计算等预处理。 光谱变换可以在一定程度上消除或减弱数据的背景噪声, 从而提高模型的反演精度[10], 提高光谱的识别率[11]。 目前已有研究分析了不同光谱变换方法对模型精度的影响[12]。 在众多光谱变换方法中, 由于微分光谱变换可以有效消除大气效应、 环境背景等影响, 从而得到了广泛的应用[13]。 目前微分光谱变换方法主要包括反射率一阶微分R'、 倒数的一阶微分(1/R)'、 指数的一阶微分(eR)'、 对数倒数的一阶微分(1/lgR)'等变换[7]。 而光谱变换方法对土壤重金属含量的反演精度有显著影响。 为了明确二者之间的响应关系, 以土壤中Ni、 Fe、 Cr、 Cu、 Pb等重金属含量为例, 对比分析了R'、 (1/R)'、 (eR)'、 (1/lgR)'等微分光谱变换方法对土壤重金属含量反演精度的影响。

在利用微分光谱数据反演土壤重金属含量时, 波段之间具有较高的相关性, 数据的冗余性较大[14], 降低了计算机的运行效率, 对反演模型的精度产生了一定的影响。 相关性分析已经广泛应用于特征波段的筛选[15], 但是, 通过相关性分析方法提取的特征变量之间仍存在共线性, 而改进离散粒子群算法(modified discrete binary particle swarm optimization, MDBPSO)可以有效降低高光谱数据的冗余性, 提高模型的反演精度[16]。 为了提高计算效率与模型精度, 可以首先通过相关性分析的方法筛选出与目标变量达到极显著相关的波段, 然后采用MDBPSO算法从中优选特征变量, 作为模型的自变量。 除特征变量外, 模型构建方法也是影响土壤重金属含量反演精度的重要因素。 综上所述, 本研究分别对光谱数据进行反射率一阶微分、 对数倒数一阶微分、 倒数一阶微分、 指数一阶微分等变换, 将相关性分析方法和MDBPSO算法结合筛选特征变量, 并利用随机森林(random forest, RF)算法构建Ni、 Fe、 Cr、 Cu、 Pb等重金属的定量反演模型。 通过对模型精度的对比分析, 研究了4种光谱变换方法的适用性, 以期对光谱变换的选择提供科学的参考。

1 实验部分
1.1 研究区概况

研究区位于陕西省西安市西咸新区(108° 31'47″—108° 58'19″E, 34° 10'15″—34° 33'16″N), 地处陕西省西安市和咸阳市建成区之间, 占地882 km2, 年平均气温13.6 ℃, 年降水量600~700 mm, 年主导风向为东北风, 属于暖温带大陆性季风半干旱、 半湿润气候区, 土壤类型主要以黄褐土、 褐土、 黄棕壤、 棕壤为代表。 研究区的地形地貌以平原与台塬为主, 呈现“ 北高南低” 阶梯状, 平均海拔为400~700 m。 目前, 随着城市化进程的加快, 研究区内部分地区的土壤受到了重金属的污染。

1.2 样品采集与测定

土壤样品采集主要在高庄镇、 六村堡、 沣西大王镇、 沣东新城等地区, 涉及到的土地类型为林地、 草地、 果园、 耕地等。 共采集了60个样点, 每个样点采集5个样品, 样品平行选取, 间隔2~5 m, 取样深度为土壤表层20 cm处。 将样品自然风干, 研磨(剔除砂砾和植物根系)后混合均匀, 然后装入聚乙烯塑料袋中密封保存。 重金属含量的测定采用原子荧光光度计AFS-2202E、 等离子体质谱仪ICP-MS等设备, 在室温25 ℃、 相对湿度50%的条件下, 测定土壤样品的Ni、 Fe、 Cr、 Cu和Pb等重金属污染元素含量。 共测定60个土壤样本的重金属含量, 其中40个样本作为训练集用于模型的构建, 其余20个样本作为检验集, 用于模型精度的评价(表1)。

表1 不同样本点土壤养分含量信息表(mg· kg-1) Table 1 Soil nutrient content at different sampling points (mg· kg-1)
1.3 光谱数据采集

室内采集土壤样品的光谱数据, 使用的仪器为SR2500地物光谱仪, 该光谱仪测量的光谱范围为350~2 500 nm, 在350~1 000 nm的波段范围内光谱分辨率为3.5 nm; 在1 000~1 900 nm波段范围内光谱分辨率为22 nm; 在1 900~2 500 nm波段范围内光谱分辨率为22 nm。 光谱测定前, 将土壤样品放在黑色器皿中, 土壤厚度约2 cm, 并对土壤表面做刮平处理。 光谱测定时, 以100 W的卤素灯作为光源, 光源距土样表面10 cm左右。 每个采样点观测5次并对观测结果取平均作为该采样点的光谱数据, 每次测量前后均用标准BaSO4参考板对数据进行校正。

1.4 光谱变换方法

已有研究表明, 光谱变换可以在一定程度上增强光谱数据在坡度上的细微变化, 去除噪声对目标光谱的影响, 从而提高光谱反射率与土壤中各个成分的相关性[17, 18]。 此外, 为了保证数据的稳定性, 首先对原始光谱进行了高斯滤波处理, 在此基础上分别对光谱数据进行反射率一阶微分R'、 倒数的一阶微分(1/R)'、 指数的一阶微分(eR)'、 对数倒数的一阶微分(1/lgR)'等微分变换。 通过差分的方法估算微分变换后的光谱数据[式(1)][19]。

Ri'=(Ri+1-Ri-1)/2Δi(1)

式(1)中, i为为各波段波长; R'i为微分光谱; Δ i为波长i+1到i-1之间的间隔。

1.5 敏感波段的选择

首先分析反射率一阶微分R'、 倒数的一阶微分(1/R)'、 指数的一阶微分(eR)'、 对数倒数的一阶微分(1/lgR)'与土壤重金属含量之间的相关性, 将相关系数(correlation coefficient, CC)满足0.001水平显著性检验的波段范围作为各土壤重金属含量的敏感特征区域。 然后采用MDBPSO算法从敏感特征区域中筛选特征变量, 用于模型的构建。

离散粒子群算法是在粒子群算法的基础上提出的一种离散群体智能随机搜索算法[20], 具有结构简单, 参数较少及易于实现等优点[21]。 与传统的离散粒子群算法相比, MDBPSO算法分别在惯性权重和粒子更新方式两个方面进行了改进, 在一定程度上提高了算法的运行效率和模型精度[22]。 采用模型的均方根误差(root mean square error, RMSE)作为MDBPSO算法的适应度函数, 以此作为各粒子优胜劣汰的评判标准。

1.6 模型构建与评价方法

已有研究表明, 随机森林(random forest, RF)算法的抗噪能力较好, 已经广泛应用于反演模型的构建[23, 24]。 基于此采用RF算法构建土壤重金含量估测模型, RF是Breiman提出的一种基于分类树的机器学习算法[25]。 该算法通过结合多种决策树算法来对同一目标进行重复预测[26], 其核心思想是通过bootstrap重采样的方法从原始的数据集中抽取一定量的样本, 并对抽取的样本进行决策树建模, 最终通过多数投票法得到模型的预测结果[27]。 利用RF算法构建土壤重金属含量的监测模型, 具体的参数设置如下: 决策树的数量(ntree)为500, 内部节点随机选择属性个数(mtry)取默认值(n/3的商, 其中n为自变量个数)。

为了保证模型的稳定性, 采用保留样本交叉检验的方法对模型精度进行评价, 将60个样本随机分为两部分, 其中40个样本作为训练集用于模型的构建, 剩余的20个样本作为检验集用于评价模型的精度。 利用模型实测重金属含量与估测重金属含量之间的R2和RMSE作为模型精度评价的标准[式(2)和式(3)], R2越高, RMSE越低, 则表示模型的估测精度越高。

RMSE=1n∑1n(yi-y^i)2(2)

R2=1-∑i=1n(yi-y^i)2∑i=1n(yi-y̅i)2(3)

式中, n为样本个数, yi为样本的实测值, y^i为模型预测值, y̅i为样本平均值。

2 结果与讨论
2.1 重金属含量与光谱关系的分析

2.1.1 不同光谱变换与土壤重金属含量相关性分析

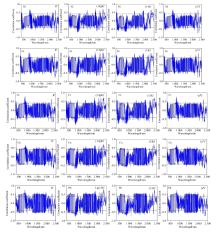
为了筛选出与研究区土壤重金属含量具有较高相关性的光谱特征敏感区域, 将微分变换后的4种土壤光谱数据与重金属含量分别进行相关性分析(图1), 并将与重金属含量满足0.001水平显著性检验的波段作为敏感特征区域。 从图1可以看出, Ni、 Fe、 Cr、 Pb和Cu等重金属含量与光谱数据中的大量波段都通过了p< 0.001水平的显著性检验。 其中, R'、 (1/lgR)'、 (1/R)'、 (eR)'与Ni达到极显著相关的波段个数分别为187、 190、 440、 199个, 与Fe达到极显著相关的波段个数分别为417、 818、 1 061、 418个, 与Cr达到极显著相关的波段个数分别为159、 458、 802、 145个, 与Cu达到极显著相关的波段个数分别为998、 1072、 987、 986个, 与Pb达到极显著相关的波段个数分别为1 101、 1 158、 1 079、 1 089个。 从图1中还可以看出, 对土壤重金属敏感的特征波段区域集中在可见光和近红外波段范围, 这主要是因为土壤中的有机质、 黏土矿物、 铁锰氧化物等组分对Ni、 Fe、 Cr、 Pb和Cu等重金属元素有存在吸附作用[28]。

图1 不同光谱变换与土壤重金属含量的相关性(n=60)
注: 图中水平线表示0.1%显著水平, R0.001[60]=0.414Fig.1 Correlations between different spectral transformations and soil heavy metal contents (n=60)
Note: Two horizontal lines indicate indicates 0.1% significant level, R0.001 [60]=0.414

2.1.2 土壤重金属含量特征波段提取

从2.1.1中可以看出通过相关性分析筛选出的特征变量依然具有较高的共线性。 基于此利用MDBPSO算法对通过相关性分析筛选出的特征变量再次进行降维。 MDBPSO算法的具体设置参数如下: 惯性权重wmax和wmin分别为0.9和0.4[29]; 学习因子c1和c2均为2; Vmax和Vmin分别为4和-4[16], 通过多次仿真训练确定最大迭代次数为200。 MDBPSO算法降维的结果如表2所示。

表2 MDBPSO算法对数据降维后的波段个数 Table 2 Number of bands after dimension reduction of data by MDBPSO algorithm

表2对比了MDBPSO算法降维前后波段个数的变化, 从表2中可以看出MDBPSO算法可以很大程度地减少了特征波段的个数, 其中R'、 (1/lgR)'、 (1/R)'、 (eR)' 4种光谱数据对Ni的敏感波段个数分别减少了157、 154、 353、 156个, 对Fe的敏感波段个数分别减少了363、 733、 984、 373个, 对Cr的敏感波段个数分别减少了135、 381、 691、 116个; 对Cu的敏感波段个数分别减少了744、 922、 803、 889, 对Pb的敏感波段个数分别减少了904、 1 032、 994、 889个。 所以MDBPSO算法可以降低数据的冗余度, 提高模型的运行效率。

2.2 模型构建及精度评价

为了更好地评估光谱变换方法对土壤重金属含量反演精度的影响, 利用MDBPSO法从对重金属含量达到极显著相关的光谱数据中优选特征波段作为遥感探测土壤重金属含量模型的输入变量, 通过RF算法构建土壤重金属含量的探测模型(图2)。 图中横坐标为重金属含量的实测值, 纵坐标为重金属含量的预测值, 实线为检验集数据的趋势线, 虚线为训练集数据的趋势线, RV2和 RT2分别为模型检验集和训练集的决定系数, RMSEV和RMSET分别为检验集和训练集的均方根误差。

图2 不同光谱变换方法的土壤重金属含量建模结果
注: —为检验集趋势线; …为训练集趋势线; □为训练集数据; ▲为检验集数据Fig.2 Modeling results of soil heavy metal content by different spectral transformation methods
Note: —is the trend line of the test set; … is the trend line of the training set; □ is the data of the training set; ▲ is the data of the test set

从图2中模型检验集的结果可以看出, Ni估测模型检验集决定系数的阶次为(1/lgR)' (0.913)> R'(0.900)> (eR)'(0.893)> (1/R)'(0.869); Fe估测模型检验集决定系数的阶次为R'(0.906)> (1/lgR)'(0.899)> (eR)'(0.892)> (1/R)'(0.856); Cr估测模型检验集决定系数的阶次为R'(0.872)> (1/lgR)'(0.839)> (1/R)'(0.788)> (eR)'(0.785); Cu估测模型检验集决定系数的阶次为(1/R)'(0.912)> (1/lgR)'(0.860)=(eR)'(0.860)> R'(0.803); Pb估测模型检验集决定系数的阶次为R'(0.876)> (1/lgR)'(0.858)> (eR)'(0.847)> (1/R)'(0.839)。 检验集的均方根误差与上述决定系数呈现出一样的排序规律, 所以Fe、 Cr、 Pb选择一阶微分变换, 而Ni和Cu分别选择对数倒数微分变换和倒数微分变换可以得到最高的模型精度。

从模型训练集的结果可以看出Ni、 Fe、 Cr、 Cu、 Pb光谱变换精度最高的方法分别是(1/R)'、 (1/lgR)'、 (1/lgR)'、 R'、 (eR)', 但是这些光谱变换方法相应的模型检验集精度并不是最高的, 说明模型的泛化能力较差, 所以不能作为重金属含量反演的最优光谱变换方法。

3 讨论

本文将高光谱数据在高斯滤波平滑的基础上分别进行一阶微分、 对数倒数微分、 倒数微分和指数微分等处理, 将相关性分析和MDBPSO算法结合对处理后的光谱数据进行降维处理, 分别筛选出对Ni、 Fe、 Cr、 Pb和Cu含量敏感的特征波段, 通过RF算法构建重金属含量估测模型, 分析不同光谱变换方法对模型精度的影响。

将对重金含量达到极显著相关的波段通过MDBPSO算法进行降维, 可以在很大程度上降低数据的冗余度, 该结果与白宗璠[22]、 张珏[16]等利用MDBPSO算法筛选对小麦条锈病病情严重度和青贮玉米原料含水率特征波段的研究结果相同或相近。 研究表明, 利用MDBPSO算法R'、 (1/lgR)'、 (1/R)'、 (eR)'中对Ni、 Fe、 Cr、 Cu和Pb敏感的特征波段个数分别至少减少了154、 363、 135、 744和889个。 这主要是因为MDBPSO算法在传统离散粒子群算法的基础上对惯性权重和粒子更新方式两个方面做出了改进, 在选择特征变量时考虑了各个波段的光谱信息对模型贡献率的问题, 可以在一定程度上解决“ 早熟” 收敛的问题[30], 所以该算法是降低数据冗余度的有效算法。

将筛选出的特征变量作为自变量构建土壤重金属含量的估测模型时, Ni估测模型精度最高的光谱变换方法为(1/lgR)', 模型的RMSEV比R'、 (1/R)'、 (eR)'分别减少了8%、 20%、 12%; Fe估测模型精度最高光谱变换方法为R', 模型的RMSEV比(1/lgR)'、 (1/R)'、 (eR)'分别减少了19%、 20%、 9%; Cr估测模型精度最高光谱变换方法为R', 模型的RMSEV比(1/lgR)'、 (1/R)'、 (eR)'分别减少了10%、 22%、 23%; Cu估测模型精度最高光谱变换方法为(1/R)', 模型的RMSEV比R'、 (1/lgR)'、 (eR)'分别减少了32%、 19%、 19%; Pb估测模型精度最高光谱变换方法为R', 模型的RMSEV比(1/lgR)'、 (1/R)'、 (eR)'分别减少了6%、 12%、 10%。 综上所述, 在利用高光谱数据估测土壤重金属含量时, Ni、 Fe、 Cr、 Cu、 Pb适宜的微分光谱变换方法分别是(1/lgR)'、 R'、 R'、 (1/R)'、 R'。

本研究仅比较了一阶微分、 对数倒数微分、 倒数微分、 指数微分4种微分光谱变换方法在土壤重金属含量探测中的适用性, 如果使用更多的光谱变换方法, (1/lgR)'、 R'、 R'、 (1/R)'、 R'是否仍是Ni、 Fe、 Cr、 Cu、 Pb的最优微分光谱变换方法需要进一步的研究。

4 结论

为了确定遥感探测土壤重金属含量最优的微分光谱变换方法, 对高光谱数据分别进行一阶微分、 对数倒数微分、 倒数微分、 指数微分等处理, 结合相关性分析和MDBPSO算法筛选对重金属含量敏感的特征变量, 利用RF算法构建了土壤重金属含量估测模型, 主要结论如下:

(1)在利用相关性分析的方法对光谱数据进行降维的基础上, MDBPSO算法可以在很大程度上对高光谱数据进行再次降维, 有效减少了数据的冗余度, 提高了模型的运行效率。 R'、 (1/lgR)'、 (1/R)'、 (eR)'中对Ni、 Fe、 Cr、 Cu和Pb敏感的特征波段个数分别至少减少了154、 363、 135、 744和889个。

(2)Ni、 Fe、 Cr、 Cu、 Pb微分光谱变换决定系数最高的方法分别是(1/lgR)'(0.913)、 R'(0.906)、 R'(0.872)、 (1/R)'(0.912)、 R'(0.876), 均方根误差最低的方法分别是(1/lgR)'(0.743)、 R'(0.095)、 R'(2.588)、 (1/R)'(1.541)、 R'(1.453)。 所以Fe、 Cr、 Pb选择一阶微分变换, 而Ni和Cu分别选择对数倒数微分变换和倒数微分变换可以得到最高的模型精度。

参考文献
[1] QIAN Jia-wei, LIU Xiao-qing, ZHANG Jing-jing, et al(钱家炜, 刘晓青, 张静静, 等). Acta Agriculturae Zhejiangensis(浙江农业学报), 2020, 32(8): 1437. [本文引用:1]
[2] LIU Yan-ping, LUO Qing, CHENG He-fa(刘彦平, 罗晴, 程和发). Journal of Agro-Environment Science(农业环境科学学报), 2020, 39(12): 2699. [本文引用:1]
[3] Liu K, Zhao D, Fang J Y, et al. Journal of the Indian Society of Remote Sensing, 2017, 45(5): 805. [本文引用:1]
[4] MA Chi(马驰). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2020, 36(20): 164. [本文引用:2]
[5] Han L, Chen R, Zhu H, et al. Sustainability, 2020, 12(4), 1476. [本文引用:1]
[6] Liu Z, Lu Y, Peng Y, et al. Remote Sensing, 2019, 11(12), 1464. [本文引用:2]
[7] GUO Yun-kai, ZHANG Qiong, QIAN Jia, et al(郭云开, 章琼, 钱佳, 等). Engineering of Surveying and Mapping(测绘工程), 2020, 29(6): 56. [本文引用:2]
[8] Tan K, Ma W, Chen L, et al. Journal of Hazardous Materials, 2021, 401: 123288. [本文引用:1]
[9] Tian S Q, Wang S J, Bai X Y, et al. Chinese Journal of Geochemistry, 2020, 39(3): 423. [本文引用:1]
[10] WANG Yu-na, LI Fen-ling, WANG Wei-dong, et al(王玉娜, 李粉玲, 王伟东, 等). Journal of Triticeae Crops(麦类作物学报), 2020, 40(11): 1389. [本文引用:1]
[11] ZHOU Ding-hao, XUE Li-hong, LI Ying, et al(周鼎浩, 薛利红, 李颖, 等). Soils(土壤), 2014, 46(1): 47. [本文引用:1]
[12] ZHANG Dong-hui, ZHAO Ying-jun, QIN Kai, et al(张东辉, 赵英俊, 秦凯, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2018, 34(20): 141. [本文引用:1]
[13] XU Kai-jian, TIAN Qing-jiu, XU Nian-xu, et al(徐凯健, 田庆久, 徐念旭, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(12): 3794. [本文引用:1]
[14] Yang C, Tan Y L, Bruzzone L, et al. Remote Sensing, 2017, 9: 782. [本文引用:1]
[15] Zhang X, Yang G, Yang Y, et al. Proc SPIE, 2016, 10156: 1015605. [本文引用:1]
[16] ZHANG Jue, TIAN Hai-qing, ZHAO Zhi-yu, et al(张珏, 田海清, 赵志宇, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2019, 35(1): 285. [本文引用:3]
[17] DING Hai-ning, CHEN Yu, CHEN Yun-zhi(丁海宁, 陈玉, 陈芸芝). Remote Sensing Technology and Application(遥感技术与应用), 2019, 34(2): 275. [本文引用:1]
[18] TONG Qing-xi, ZHANG Bing, ZHENG Lan-fen(童庆禧, 张兵, 郑兰芬). Hyperspectral Remote Sensing-Principles, Techniques and Applications(>高光谱遥感——原理、 技术与应用), Beijing: Higher Education Press(北京: 高等教育出版社), 2015. [本文引用:1]
[19] PU Rui-liang, GONG Peng(浦瑞良, 宫鹏). Hyperspectral Remote Sensing and Its Applications(高光谱遥感及应用), Beijing: Higher Education Press(北京: 高等教育出版社), 2003. [本文引用:1]
[20] Kennedy J, Eberhart R. A Discrete Binary Version of the Particle Swarm Algorithm. International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, 1997, 5: 4104. [本文引用:1]
[21] CAO Yin, YE Yun-tao, ZHAO Hong-li, et al(曹引, 冶运涛, 赵红莉, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2018, 49(1): 173. [本文引用:1]
[22] BAI Zong-fan, JING Xia, ZHANG Teng, et al(白宗璠, 竞霞, 张腾, 等). Acta Agronomica Sinica(作物学报), 2020, 46(8): 1248. [本文引用:2]
[23] Wang L, Zhou X D, Zhu X K, et al. The Crop Journal, 2016, 4(3): 212. [本文引用:1]
[24] YAO Xiong, YU Kun-yong, YANG Yu-jie, et al(姚雄, 余坤勇, 杨玉洁, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2017, 48(5): 159. [本文引用:1]
[25] Breiman L. Machine Learning, 2001, 45(1): 5. [本文引用:1]
[26] Rodriguez-Galiano V, Mendes M P, Garcia-Soldado M J, et al. Science of the Total Environment, 2014, 476-477: 189. [本文引用:1]
[27] WANG Li-ai, MA Chang, ZHOU Xu-dong, et al(王丽爱, 马昌, 周旭东, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2015, 46(1): 259. [本文引用:1]
[28] XIE Xian-li, SUN Bo, HAO Hong-tao(解宪丽, 孙波, 郝红涛). Acta Pedologica Sinica(土壤学报), 2007, 44(6): 982. [本文引用:1]
[29] ZHANG Hui-juan, ZHANG Da-min, YAN Wei, et al(张绘娟, 张达敏, 闫威, 等). Computer Science(计算机科学), 2019, 46(10): 109. [本文引用:1]
[30] Cao Y, Ye Y T, Zhao H L, et al. Ecological Informatics, 2018, 44: 21. [本文引用:1]