三尺度分解和稀疏表示的红外和可见光图像融合

引用本文

冀鲸宇, 张玉华, 邢娜, 王长龙, 林志龙, 姚江毅. 三尺度分解和稀疏表示的红外和可见光图像融合[J]. 光谱学与光谱分析, 2024,44(5): 1425-1438.
JI Jing-yu, ZHANG Yu-hua, XING Na, WANG Chang-long, LIN Zhi-long, YAO Jiang-yi. Three-Scale Deconstruction and Sparse Representation of Infrared and Visible Image Fusion[J]. Spectroscopy and Spectral Analysis, 2024,44(5): 1425-1438.
Doi:10.3964/j.issn.1000-0593(2024)05-1425-14 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

三尺度分解和稀疏表示的红外和可见光图像融合

冀鲸宇, 张玉华, 邢娜, 王长龙, 林志龙^*, 姚江毅

陆军工程大学石家庄校区, 河北石家庄 050003

*通讯作者 e-mail: 601386022@qq.com

作者简介: 冀鲸宇, 女, 1998年生, 陆军工程大学石家庄校区博士研究生 e-mail: whale982022@163.com

收稿日期: 2022-01-12 修订日期: 2023-08-28

基金: 基础加强计划技术领域基金项目(2019-xxx), 军内科研重要项目(xx2019-xxx)资助

摘要

为提高对含噪声源图像的处理效果, 以及提高融合图像的对比度、结构信息等, 提出一种基于三尺度分解和稀疏表示的红外和可见光图像融合算法。首先, 为增强对噪声的去除效果, 并且维持源图像的结构和边缘特性, 利用滚动引导滤波器对源图像进行分解, 将源图像分解为基础层和细节层; 其次, 为充分利用基础分量中的细节和能量, 同时降低模型的复杂性, 构造结构-纹理分解模型, 将基础层再次分解为基础结构层和基础纹理层。然后分析三个分量的不同特点, 使用不同的融合规则对三个分量分别进行融合, 针对细节分量, 其含有主要的噪声成分, 但含噪声程度又不一样, 因此根据图像含噪声的程度自适应确定稀疏融合去噪参数, 从而同时实现对细节分量的融合和去噪, 并且能够有效地提高计算效率; 针对基础结构分量, 其包含的细节特征较少, 直接采用基于视觉显著图的加权平均技术进行预融合; 针对基础纹理分量, 由于其包含了视觉上重要的信息或图像特征, 如边缘、直线和轮廓等活动信息, 能够反映出原始基础图像的主要细节, 因此采用主成分分析方法进行预融合, 最终通过重构细节、基础结构和基础纹理层来得到融合图像。为验证所提方法的有效性, 选取了多组红外和可见光图像进行试验, 并与近期的五种方法CNN、 FPDE、 ResNet、 IFEVIP、 TIF进行了对比, 采用主观和客观的形式对结果进行分析。实验结果表明, 同其他图像融合算法进行对比分析, 该方法能够兼顾含噪声和无噪声图像的融合, 在有无噪声的情况下均能够将源图像的细节、亮度和结构保留到融合图像中, 而且能有效地消除噪声。

关键词: 图像融合; 噪声图像融合; 滚动引导滤波; 三尺度分解; 稀疏表示

中图分类号:TP391 文献标志码:A

Three-Scale Deconstruction and Sparse Representation of Infrared and Visible Image Fusion

JI Jing-yu, ZHANG Yu-hua, XING Na, WANG Chang-long, LIN Zhi-long^*, YAO Jiang-yi

Army Engineering University Shijiazhuang Campus, Shijiazhuang 050003, China

*Corresponding author

Abstract

To improve the processing performance of source images with noise and improve the contrast and structural information of the fused images, an infrared and visible image fusion algorithm based on three-scale decomposition and sparse representation is proposed. First, to enhance the noise removal effect and maintain the structure and edge characteristics of the source image, the rolling guidance filter is used to decompose the source image, and the source image is decomposed into the base layer and the detail layer. Secondly, in order to make full use of the details and energy in the base component and reduce the complexity of the model, a structure-texture decomposition model is constructed. The base layer is decomposed into the base structure layer and base texture layer again, Then by analyzing the different characteristics of the three components, different fusion rules are utilized to fuse the three components respectively. The detail component contains the main noise components, but the noise level is different. Therefore, the sparse fusion denoising parameter is adaptively determined according to the noise level of the image to realize the fusion and denoising of the detail component at the same time and can effectively improve computational efficiency; for the base structure components, which contain fewer detail features, the weighted average technology based on the visual saliency map is directly used for pre-fusion; for the base texture components, because they contain visually important information or image features, such as edges, lines and contours and other activity information, which can reflect the main details of the original base image, the principal component analysis method is used for pre-fusion. Finally, the fused image is obtained by reconstructing the detail, base structure and texture layers. In order to verify the effectiveness of the proposed method, several groups of infrared and visible images were selected for experiments and compared with five recent methods, including CNN, FPDE, ResNet, IFEVIP and TIF, and the results were analyzed in a subjective and objective form. The experimental results show that, compared with other image fusion algorithms, this method can consider the fusion of noise-perturbed and noise-free images and can retain the details, brightness and structure of the source image in the fusion image with or without noise. Moreover, can effectively eliminate noise.

Keyword: Image fusion; Noise-perturbed image fusion; Rolling guidance filter; Three-scale decomposition; Sparse representation

文章图片

引言

近年来, 无人机凭借其高灵活度、低成本以及易操作等优势在多个领域发挥着越来越重要的作用, 在军事上, 其常用于执行战场侦察及态势监控等任务。然而, 随着战场实际需要的多样化及复杂化, 单一成像传感器受限于自身的物理成像原理, 只能感知部分目标或战场信息, 很难完成多种目标背景下的探测和识别任务^[1]。因此, 通过融合多种传感器图像数据以实现不同传感器数据之间的互补, 可以得到更加直观、可靠和全面的目标或场景, 进而为后续特征提取、目标识别和检测等任务提供强有力的数据支持, 便于做出更加合理的决策^[2]。

图像融合大多是在像素级进行研究, 其中, 依据图像表示和融合过程的不同, 图像融合大致可以分为四类: 基于空间域的方法^[3], 基于变换域的方法^[4], 基于神经网络的方法^[5]和基于字典学习的方法^[6]。当前许多图像融合方法大都假设源图像无噪声, 对噪声扰动情况的研究较少。然而, 由于成像设备、拍摄环境等诸多因素的影响, 实际任务中获取的图像不可避免的存在噪声, 直接进行图像融合时源图像中的噪声和细节信息可能被同等处理, 导致融合效果不佳。针对噪声图像的融合, 通常采用先融合后去噪或先去噪后融合的分步方法, 即将去噪算法和融合算法相结合, 实现融合去噪。然而, 从效率和聚变性能的角度来看, 分步推进的方式可能不是最好的选择。为解决这一问题, 出现了一些同步融合去噪方法^{[7, 8, 9, 10, 11]}, 其中基于稀疏表示(sparse representation, SR)的方法可同时解决图像融合和去噪两个问题。

文献[7]提出了一种有效的基于SR的图像去噪算法, 该方法建立了噪声标准差与稀疏重建误差之间的联系, 能够以参数自适应的方式有效地实现图像去噪。随后, 一些学者提出了基于SR的联合图像去噪融合算法。 Yang等^[8]设计的方法实现了融合与去噪的同步。为进一步提高融合性能, 解决融合耗时长的问题, Liu等^[9]提出了一种自适应SR方法用于图像融合和去噪, 该方法根据训练样本的梯度特征对多个特征字典进行预训练, 再根据图像梯度特征自适应选择合适的字典, 可以有效地实现图像的融合和去噪。 Kim等^[10]通过引入核局部回归权值进行特征聚类, 设计了一种基于字典学习的多模态图像融合方法, 该方法能有效地抑制噪声产生, 且融合降噪性能良好。为降低直接用SR处理的噪声源图像去噪时可能会对图像的边缘信息造成的损伤, Li等^[11]提出了一种基于稀疏低秩字典学习的医学图像融合方法。在该方法中, 源图像被看作是粗尺度和细尺度分量的叠加, 有效的解决了上述问题。

然而, 以上研究不能同时兼顾无噪声和有噪声的图像融合, 为解决此问题, 在此提出一种基于三尺度分解和稀疏表示的红外和可见光图像融合算法。首先, 设计一种三尺度分解模型, 通过滚动引导滤波将图像分解为基础分量和细节分量, 再通过结构-纹理分解对基础层进行处理, 有效提取基础分量中的详细纹理信息, 以提高融合图像表达细节信息的能力; 其次, 提出一个稀疏融合去噪参数, 根据含噪程度自适应得到该参数值, 有效处理图像融合中的噪声问题, 从而兼顾噪声图像和无噪声图像融合问题。

1 关键理论分析

1.1 滚动引导滤波

滚动引导滤波(rolling guidance filter, RGF)具有尺度感知和边缘保持的特性。因此, 其不仅对噪声的去除能力较好, 而且能够维持源图像的结构和边缘特性。 RGF包括两个主要步骤: 小结构去除和边缘恢复^[12]。

首先利用高斯滤波器去除小结构, 从输入图像I中过滤的图像G可表示为

$G = Gaussian (I, σ_{s})$ (1)

式(1)中, Gaussian(I, σ _s)表示以标准差σ _s作为尺度参数的高斯滤波, 通过该滤波器可以去除规模小于规模空间的结构信息。

然后使用引导滤波器^[13]进行迭代边缘恢复, 因为它具有较高的计算效率和良好的边缘保持特性。该步骤是一个恢复的图像J^t迭代更新的过程, 且初始图像J¹是高斯平滑图像G。第t次迭代可以表示为

$J^{t + 1} = GuidedFilter (J^{t}, I, σ_{s}, σ_{r}^{2})$ (2)

式(2)中, GuidedFilter(J^t, I, σ _s, ${σ_{r}}^{2}$ )为引导滤波, 其中I, σ _s即式(1)中的参数, J^t为引导图像, σ _r控制距离权值。在此, 设σ _r=0.05。 RGF是结合式(1)和式(2)来完成的, 可表示为

$u = RGF (I, σ_{s}, σ_{r}, T)$ (3)

式(3)中, T为迭代次数, u为滤波输出。

1.2 结构-纹理分解

图像I可以分解为I=S+T, 即看作是结构成分S和纹理成分T的叠加。在结构-纹理分解模型^[14]中, 结构成分主要由一些非重复的边缘和平滑的能量区域组成, 而纹理成分则是重复的振荡信息和噪声。为此, 定义了结构纹理的局部特征, 并提出了区间梯度算子。将离散信号I中的像素p的区间梯度滤波器(interval gradient filter, IGF)定义为∇_Ω(· ), 其可以表示为

${(\nabla}_{Ω} {I)}_{p} = g_{\tilde{φ}}^{r} (I_{p}) - g_{\tilde{φ}}^{l} (I_{p})$ (4)

式(4)中, Ω 是中心像素p附近的区域, $g_{\tilde{φ}}^{l}$ 和 $g_{\tilde{φ}}^{r}$ 分别是左、右剪切一维高斯函数, 其中

$g_{\tilde{φ}}^{r} (I_{P}) = \frac{1}{k_{r}} \sum_{n \in Ω (p)} ω_{\tilde{φ}} (n - p - 1) I_{n}$ (5)

$g_{\tilde{φ}}^{l} (I_{P}) = \frac{1}{k_{l}} \sum_{n \in Ω (p)} ω_{\tilde{φ}} (p - n) I_{n}$ (6)

式(5)和式(6)中, $ω_{\tilde{φ}}$ 为剪切指数加权函数, $\tilde{φ}$ 为标度参数。

$ω_{\tilde{φ}} (x) = \{\begin{array}{l} \exp (- \frac{x^{2}}{2 {\tilde{φ}}^{2}}), & x \geq 0 \\ 0, & x < 0 \end{array}$ (7)

定义k_r和k_l是标准化系数, 表示为

$k_{r} = \sum_{n \in Ω (p)} ω_{\tilde{φ}} (n - p - 1)$ (8)

$k_{l} = \sum_{n \in Ω (p)} ω_{\tilde{φ}} (p - n)$ (9)

与传统的正向微分不同, 区间梯度测量的是像素左右两边的加权平均差值。为了获得结构信息, 结构区域中不应该存在纹理信息, 结构区域的局部窗口Ω (p)只能包含增加或减少的信息, 不能包含重复的纹理。

将输入信号I的梯度细化为如下的区间梯度

${(\tilde{\nabla} I)}_{p} = \{\begin{array}{l} {(\nabla I)}_{p} ω_{p}, & sign [{(\nabla I)}_{p}] = sign [(\nabla_{Ω} {I)}_{p}] \\ 0, & otherwise \end{array}$ (10)

式(10)中, ( $\tilde{\nabla}$ I)_p为标度梯度, ω _p为标度权值, 表示为

$ω_{p} = \min (1, \frac{| (\nabla_{Ω} {I)}_{p} | + ε}{{(\nabla I)}_{p} + ε})$ (11)

式(11)中, ε 为小常数, 通常设置为10^-4。

为了消除信号中残留的振荡信号, 得到输入信号的结构分量, 在引导滤波的基础上, 由回归梯度得到临时滤波结果

$R_{p} = \overset{p - 1}{\sum_{k = 0}} I_{0} + {(\tilde{\nabla} I)}_{k}, p \in {0, 1, \dots, N_{p}}$ (12)

式(12)中, N_p表示I中的像素数, I₀为I中的最小值(最左)。通过求解式(13)可得到一维信号引导滤波的最优系数a_p和b_p。

$\underset{a_{p}, b_{p}}{argmin} \sum_{n \in N (p)} ω_{n} [(a_{p} R_{n} + b_{p} - I_{n})^{2} + λ {a_{p}}^{2}]$ (13)

$ω_{n} = \exp (- \frac{{(n - P)}^{2}}{2 {\tilde{φ}}^{2}})$ (14)

式(13)和式(14)中, ω _n表示高斯权值, $\tilde{φ}$ 为式(5)中定义的标度参数, λ 表示平滑参数, 系数a_p和b_p定义为

$a_{p} = \frac{g_{\tilde{φ}} [{(RI)}_{p}] - g_{\tilde{φ}} (R_{p}) g_{\tilde{φ}} (I_{p})}{g_{\tilde{φ}} (R_{p}^{2}) - g_{\tilde{φ}} (R_{p})^{2} + λ}$ (15)

$b_{p} = g_{\tilde{φ}} (I_{p}) - a_{p} g_{\tilde{φ}} (R_{p})$ (16)

得到系数a_p和b_p后, 可通过S_p= $g_{\tilde{φ}}$ (a_p) R_p+ $g_{\tilde{φ}}$ (b_p)得到信号I的结构分量。

对于二维图像信号, 利用一维信号在x和y方向上交替的区间梯度滤波, 以迭代的方式收敛得到最终图像的结构层^[15]。由图1中图像放大的区域可以看出, 几乎所有的振动和重复信息都被保留到了纹理层, 而亮度和弱边缘信息则被保留到了结构层。

	Figure Option View Download New Window
	图1 图像结构-纹理分解Fig.1 Image structure-texture decomposition

2 三尺度分解和稀疏表示模型

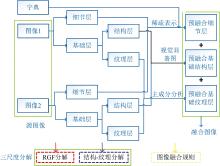
为解决在去噪的同时有效保留细节的问题, 构建一种新的图像融合模型, 如图2所示。与传统的双尺度分解方案不同, 为了更好地去噪和利用基础层的有用信息, 首先利用RGF将源图像分解为基础和细节分量, 此时大部分细节和外部噪声都能被有效地保留到细节层中, 基础层则包含残差细节和能量; 然后对基础层进行结构-纹理分解, 最终源图像被分解为细节、基础结构和基础纹理三个分量。根据每一层的特点, 采用三种融合规则生成各层的预融合图像。其中, 对于细节层的融合, 通过建立稀疏重构误差与噪声标准差之间的联系, 有效实现融合去噪; 对于基础结构层, 采用基于视觉显著图(visual saliency map, VSM)的加权平均技术进行预融合; 对于基础纹理层, 采用主成分分析方法进行预融合。最后, 通过重构三层预融合层得到融合结果。

	Figure Option View Download New Window
	图2 提出的融合去噪方法结构图Fig.2 Schematic diagram of the proposed image fusion and denoising method

2.1 分解模型

为了有针对性地去除附着在图像中的噪声, 首先对源图像进行基础和细节分解

$I_{n}^{b} = RGF (I_{n}, σ_{s}, σ_{r}, T)$ (17)

式(17)中, I_n是第n个源像, n∈ {1, 2, …, N}, $I_{n}^{b}$ 表示I_n的基础层, 通过求解 $I_{n}^{b}$ , 得到图像I_n的细节层 $I_{n}^{d}$ 。

$I_{n}^{d} = I_{n} - I_{n}^{b}$ (18)

对于基础层融合通常采用绝对值-最大或平均的方法^[17], 但这些方法产生的融合结果可能会由于对比度降低和边缘退化而变差。但对图像进行多次分解仍不能将图像基础、细节信息很好地分离, 且多次分解必然会增加重构过程的复杂性, 导致结果不佳。为解决此问题, 引入结构-纹理分解模型对 $I_{n}^{b}$ 进行分解, 得到其结构层 $I_{n}^{b, s}$

$I_{n}^{b, s} = IGF (I_{n}^{b}, \tilde{φ}, λ)$ (19)

式(19)中, $\tilde{φ}$ 和λ 分别为标度参数和平滑参数。 $I_{n}^{b}$ 的纹理层可以通过式(20)生成

$I_{n}^{b, t} = I_{n}^{b} - I_{n}^{b, s}$ (20)

经过上述操作, 得到图像的细节层、基础结构层和基础纹理层。

图3中的每一组图像包含一个无噪声图像和相应的噪声图像, 这两组图像验证了提出的三尺度分解方法的有效性, 特别是对于有噪声的输入图像。由图3可知:

	Figure Option View Download New Window
	图3 三尺度分解图像(在第二和第四行输入图像中加入σ =30的高斯白噪声)Fig.3 Three-layer decomposition images (Gaussian white noise with σ =30 is added to the input images of the second and fourth rows)

(1)通过RGF进行分解, 大部分噪声和细节保留到细节层。同时, 可以看到基础层仍然包含一定的细节信息。

(2)经过结构-纹理分解处理后, 结构层几乎不包含局部振荡信息, 局部区域通常只包含强度信息或少数明显的边缘结构。

(3)无噪声和噪声图像产生的结构和纹理层非常相似, 即噪声信息几乎完全存在于细节层中。

2.2 融合规则

根据三个部分的特点, 设计了三种不同的融合规则。

2.2.1 细节层融合

基于SR的方法可以很好地实现细节层的融合去噪。包括两个步骤: 字典学习和稀疏系数生成。在第一阶段, 通过式(14)的滚动引导滤波器生成训练数据的细节层, 从细节图像中收集8× 8大小的块, 构建最终的训练集, 采用KSVD^[17]算法可以得到过完备字典D。在第二阶段, 对每个源图像取8× 8大小的块, 并对其进行归一化, 通过求解以下目标函数, 采用正交匹配追踪算法(orthogonal matching pursuit, OMP)^[18]生成细节层SR系数

$\min_{α_{n}^{k}} ‖ α_{n}^{k} ‖_{0}, s.t. ‖ V_{n}^{k} - D α_{n}^{k} ‖_{0} < E$ (21)

式(21)中, $V_{n}^{k}$ 为源图像I_n的第k个小块, $α_{n}^{k}$ 为对应的稀疏向量。 E为稀疏融合去噪参数, 定义为

$E = \{\begin{array}{l} P, & σ = 0 \\ 0.005 + 8 Cσ, & σ > 0 \end{array}$ (22)

式(22)中, σ 为高斯标准差, C> 0是在σ > 0时控制E的参数。然后采用“ 绝对值-最大” 方案生成融合稀疏系数

$\begin{array}{l} α_{F^{d}}^{k} = α_{\tilde{n}}^{k}, \\ \tilde{n} = \underset{n}{argmax} {‖ α_{n}^{k} ‖_{1} | n = 1, 2, \dots, N} \end{array}$ (23)

融合细节矢量 ${\overset{̅}{α}}_{F^{d}}^{k}$ 可由式(24)线性表示得到

${\overset{̅}{α}}_{F^{d}}^{k} = D α_{F^{d}}^{k}$ (24)

将每个 ${\overset{̅}{α}}_{F^{d}}^{k}$ 重塑为8× 8的小块, 然后根据初始位置进行排列, 得到融合细节层。

2.2.2 基础结构层融合

由于基础结构层来自源图像的基础分量, 因此该层包含的细节较少, 如图3第四列的图像所示。因此, 采用基于VSM^[18]的加权平均技术融合基础结构层F^b^,^s。

首先构造VSM, 让I_P代表图像I中的一个像素p的强度值。像素p的显著值V(p)被定义为

$V (p) = \overset{L - 1}{\sum_{j = 0}} M_{j} | I_{P} - I_{j} |$ (25)

式(25)中, N表示I中的像素总数, j代表像素强度, M_j代表强度等于j的像素数, L表示灰度级数(在此为256)。如果两个像素友相同的强度值, 其显著值是相等的。然后将V(p)归一化到[0, 1]。

设V₁和V₂分别表示不同源图像的VSMs, $I_{1}^{b, s}$ 和 $I_{2}^{b, s}$ 表示不同源图像的基础结构层图像, 通过加权平均得到最终的基础结构层融合图像

$F^{b, s} = W_{b} I_{1}^{b, s} + (1 - W_{b}) I_{2}^{b, s}$ (26)

式(26)中权重W_b被定义为

$W_{b} = 0.5 + \frac{V_{1} - V_{2}}{2}$ (27)

2.2.3 基础纹理层融合

与基础结构层相比, 基础纹理层包含了视觉上重要的信息或图像特征, 如边缘、直线和轮廓等活动信息, 能够反映出原始基础图像的主要细节。因此, 采用主成分分析方法^[19]来有效检测这些特征。

将可见光和红外图像的基础纹理图像 $I_{VI}^{b, t}$ 和 $I_{IR}^{b, t}$ 作为矩阵γ 的列向量。再将每一行作为一个参考, 每一列作为一个变量, 求出γ 的协方差矩阵C。

计算C的特征值λ ₁, λ ₂以及相对应的特征向量 $ϕ_{1} = (\begin{array}{l} Φ_{1} (1) \\ Φ_{1} (2) \end{array}] 和 ϕ_{2} = (\begin{array}{l} Φ_{2} (1) \\ Φ_{2} (2) \end{array}] 。$

从两个特征值中找出最大的特征值, 即λ _max=max(λ ₁, λ ₂)。将相对应于λ _max的特征向量作为最大特征向量ϕ _max。计算出对应于ϕ _max的主成分, 分别将其值归一化作为融合权重P₁和P₂, 得到最终的基础纹理图像F^b^,^t

$F^{b, t} = P_{1} I_{VI}^{b, t} + P_{2} I_{IR}^{b, t}$ (28)

得到这三个预融合分量后, 最终的融合图像F为

$F = F^{d} + F^{b, s} + F^{b, t}$ (29)

3 实验和结果讨论

使用五对红外和可见光源图像, 图像源可从公共网站http://imagefusion.org/获得, 如图4所示。并且选择了五个近期的方法, 包括CNN^[20]、 FPDE^[21]、 ResNet^[22]、 IFEVIP^[23]、 TIF^[24], 将其在同样的实验环境下进行对比验证, 采用熵EN^[25]、边缘信息保留度 $Q_{AB / F}$ ^[26]、 Chen-Blum提出的指标 $Q_{CB}$ ^[27]、互信息MI^[28]、 Wang等提出的指标 $Q_{W}$ ^[29]、 Yang等提出的指标 $Q_{Y}$ ^[30]6个指标对融合结果进行定量评价。

	Figure Option View Download New Window
	图4 五对源图像Fig.4 Five pairs of source images

3.1 参数设置

本节主要对式(22)中的自由参数C进行分析。由于模型中的去噪过程仅针对细节分量, 为直观分析不同C下的融合去噪性能, 仅对细节层融合结果进行分析, 如图5所示。以图5中(a1, a2)、 (b1, b2)两对图像为例, 分别加入σ =20的高斯噪声, 生成不同C的融合图像。

	Figure Option View Download New Window
	图5 不同C值在细节层融合和去噪的结果(噪声水平20)Fig.5 Fusion and denoising performance results in detail layer(noise level 20)

对于图5(a1)和(a2)图像融合, 可以看出: ①当C< 0.003 5, 融合图像中的噪声相对明显[图5(a3—a7)], 特别是当C是远远低于0.003 5, 去噪效果有限; ②当C=0.003 5时, 大部分噪声已经消除; ③当C> 0.003 5时, 噪声几乎不存在, 但此时, 融合图像出现过平滑效应。因此, C=0.003 5是一个明显的分界值, 从细节保护角度来看, C=0.003 5可达到该图像对融合的最佳视觉效果。同理, 对另一组灰度图像融合结果进行分析[图5(c3—c10)], 也可得出同样的结论。因此, 对于灰度图像的融合, C的最佳值为0.003 5。

对于图5(b1)和(b2)图像融合, 可以看出: ①当C< 0.002时, 融合图像中存在一些噪声[图5(b3—b4)]; ②当C=0.002时, 噪声得到大大降低和抑制, 同时细节保存较好[图5(b5)]; ③当C> 0.002时, 去噪性能较好, 但图5(b6—b10)中的细节或多或少被破坏, 一些细微的边缘被平滑, 并且随着C的增加, 越来越多的细节被遗漏了。同理, 对另一组彩色图像融合结果进行分析[图5(d3—d10)], 也可得出同样的结论。因此, 综合考虑融合和去噪的性能, 对于彩色图像融合, C的最佳值为0.002。

此外, 式(17)中RGF的参数T设为4, 式(19)区间梯度滤波参数设为 $\tilde{φ}$ =3, λ =0.03², σ _s设置为3, 式(22)中的参数P设为0.001。

3.2 无噪声图像融合与评价

图6为三对无噪声红外与可见光灰度图像融合示例, 图7为两对无噪声红外可见光彩色图像融合示例, 其中图6(a1, b1, c1)和图7(a1, b1)为红外图像, 图6(a2, b2, c2)和图7(a2, b2)为可见光图像; 图6(a3—a8, b3—b8, c3—c8)和图7(a3—a8, b3—b8)为不同方法得到的融合结果。

	Figure Option View Download New Window
	图6 无噪声红外可见光灰度图像融合结果Fig.6 Fused results of noise-free infrared/visible images

	Figure Option View Download New Window
	图7 无噪声红外可见光彩色图像融合结果Fig.7 Fused results of noise-free infrared/visible images

3.2.1 主观评价

从图6可以看出, FPDE和ResNet方法得到的融合图像与所提出的方法得到的结果图相比对比度更低; CNN、 IFEVIP方法保持了良好的对比度, 但视觉效果过于增强, 导致融合结果不自然, 存在明显误差; TIF方法存在内部特征模糊的现象。因此, 在融合结果中, 本方法可以有效地分离出不同图像的分量信息, 结合各自的融合规则可将源图像的有用信息传递到融合图像中, 在对比度和细节保持方面获得了最佳的视觉性能。

从图7可以看出, FPDE、 ResNet、 TIF方法的亮度明显低于IFEVIP和CNN方法, 但CNN方法存在色彩偏差效果, IFEVIP方法引入了伪影。 FPDE和ResNet方法虽然结构得到了较好的保存, 但细节相对弱化和丢失。总体上看, 图7(a8)和(b8)中的亮度、结构和细节与其他方法相比表现出了更好的性能, 这意味着所提方法可以产生更优的视觉效果。以上分析验证了本方法在无噪声图像融合上具有更好的效果。

3.2.2 客观评价

除主观视觉分析外, 对上述融合结果进行定量评价, 结果如表1所示。根据表中数据可以看出, 本方法的客观评价显著高于其他方法, 特别是对于指标EN、 Q_CB和Q_Y总是表现得更优。在所有的量化评估中, 只有个别地方不是最佳的, 但这并不影响本方法的优势。

表1 无噪声图像融合结果定量指标 Table 1 Quantitative indices of noise-free image fusion results

综上, 对于无噪声图像融合, 本方法在主观和客观上都具有良好的表现。

3.3 噪声扰动图像融合与评价

图8为一对含噪声红外与可见光灰度图像融合示例, 图9为一对含噪声红外可见光彩色图像融合示例, 其中(a1—a2, b1—b2, c1—c2)分别为加入10级、 20级和30级高斯噪声的扰动源图像, (a3—a8, b3—b8, c3—c8)为不同方法得到的融合结果。

	Figure Option View Download New Window
	图8 含噪声红外可见光灰度图像融合结果Fig.8 Fused results of noise-perturbed infrared/visible grayscale images

	Figure Option View Download New Window
	图9 含噪声红外可见光彩色图像融合结果Fig.9 Fused results of noise-perturbed infrared/visible colour images

3.3.1 主观评价

从图8、图9含噪声图像融合结果可以看出:

①当高斯噪声水平为10时, FPDE、 IFEVIP和TIF方法的去噪能力有限, 其融合结果不能很好地保留有用信息; ResNet和CNN方法能在一定程度上有效去噪, 但会引起细节对比缺失, 这两种方法可以在噪声环境下进行融合, 但会引入一些不相关的信息, 从而导致不真实的视觉效果。与其他方法相比, 本方法在细节保持方面具有最好的融合能力, 同时融合结果中噪声显著降低, 具有良好的去噪性能。

②当噪声水平达到20时, CNN、 FPDE、 IFEVIP和TIF方法产生的融合结果的结构会受到严重的破坏, 大量明显的误差信息会被引入融合结果中。 ResNet方法在一定程度上抑制了噪声, 但出现了对比度降低和过度平滑现象。相比之下, 本文提出的方法不仅能将源图像的细节、亮度和结构保留到融合图像中, 而且能有效地消除噪声, 具有良好的去噪性能。

③当噪声等级为30时, CNN、 FPDE、 ResNet、 IFEVIP和TIF方法中的细节和小结构被破坏, 并且均存在噪声。通过对比, 本方法不仅保留了对比度和结构, 而且有效、适当地去噪, 从而获得了更好的融合性能。

基于以上主观分析, 本方法可以有效地实现图像融合和去噪的同步进行, 并且相比于一些经典的方法产生更好的视觉效果。

3.3.2 客观评价

不同方法产生的噪声融合结果的客观评价如表2—表4所示。与五种传统的图像融合方法相比, 该方法能得到更好的定量评价, 与无噪声图像融合客观评价结果基本一致。这验证了所提方法的有效性和优越性。

表2 σ =10时图像融合结果定量指标 Table 2 Quantitative indices of image fusion results (σ =10)

表3 σ =20时图像融合结果定量指标 Table 3 Quantitative indices of image fusion results (σ =20)

表4 σ =30时图像融合结果定量指标 Table 4 Quantitative indices of image fusion results (σ =30)

综上, 对于含噪声图像融合, 本方法在主观和客观上都具有良好的表现。

3.4 计算效率

测试的方法均在相同的实验环境进行, 对于所有图像的平均实现时间的比较, 如表5所示。由表可见, 本方法的计算效率虽然不是最高的, 但比CNN、 ResNet这类方法仍有一些优势。在未来, 改进算法的计算效率是研究的重点。

表5 不同方法的计算效率 Table 5 Computation efficiencies of different methods

4 结论

提出了一种基于三尺度分解和稀疏表示的红外和可见光图像融合去噪方法, 充分利用了RGF和结构纹理分解方法的优点。并采用稀疏表示对细节层图像进行融合, 根据含噪程度自适应确定稀疏融合去噪参数, 从而得到融合的细节层图像。从实验结果可得出所提方法可兼顾无噪声图像融合和含噪声图像融合。特别的是, 为便于分析, 本文只讨论了两个源图像的情况, 但在实际应用中可以将所提出的方法推广到两个以上源图像的融合问题中。

参考文献

文献列表

[1]	SHEN Yu, YUAN Yu-bin, PENG Jing, et al(沈瑜, 苑玉彬, 彭静, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(7): 2023. [本文引用:1]
[2]	Angel Y, Turner D, Parkes D, Parkes S, et al. Remote Sensing, 2020, 12(1): 34. [本文引用:1]
[3]	Li S, Kwok J T, Wang Y. Information Fusion, 2001, 2(3): 169. [本文引用:1]
[4]	Kong Weiwei. Infrared Physics & Technology, 2014, 63: 110. [本文引用:1]
[5]	Long J, Shelhamer E, Darrell T. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(4): 640. [本文引用:1]
[6]	Li S, Yin H, Fang L. IEEE Transactions on Bio-Medical Engineering, 2012, 59(12): 3450. [本文引用:1]
[7]	Elad M, Aharon M. Image Denoising Via Learned Dictionaries and Sparse Representation. IEEE Computer Society Conference on Computer Vision & Pattern Recognition. New York, USA: IEEE, 2006: 3736. [本文引用:2]
[8]	Yang B, Li S. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 884. [本文引用:2]
[9]	Liu Y, Wang Z. IET Image Processing, 2015, 9(5): 347. [本文引用:2]
[10]	Kim M, Han D K, Ko H. Information Fusion, 2016, 27: 198. [本文引用:2]
[11]	Li H, Wang Y, Yang Z, et al. IEEE Transactions on Instrumentation and Measurement, 2020, 69(4): 1082. [本文引用:2]
[12]	Zhang Qi, Shen X Y, Xu L, et al. Rolling Guidance Filter. European Conference on Computer Vision, 2014. [本文引用:1]
[13]	He K, Sun J, Tang X. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 35: 1397 [本文引用:1]
[14]	Lee H, Jeon J, Kim J, et al. Computer Graphics Forum, 2017, 36(6): 262. [本文引用:1]
[15]	Zhu B, Liu J Z, Cauley S F, et al. Nature, 2017, 555(7697): 487. [本文引用:1]
[16]	Aharon M, Elad M, Bruckstein A. IEEE Transactions on Signal Processing, 2006, 54(11): 4311. [本文引用:1]
[17]	Donoho D L, Tsaig Y, Drori I, et al. IEEE Transactions on Information Theory, 2012, 58(2): 1094. [本文引用:2]
[18]	Cheng M N, Mitra N J, Huang X, et al. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 37(3): 569. [本文引用:2]
[19]	Gonzalez R C, Woods R E, Masters B R. Journal of Biomedical Optics, 2009, 14: 029901. [本文引用:1]
[20]	Liu Y, Chen X, Cheng J, et al. International Journal of Wavelets, Multiresolution and Information Processing, 2018, 16(3): 1850018. [本文引用:1]
[21]	Bavirisetti D P, Xiao G, Liu G. Multi-Sensor Image Fusion Based on Fourth Order Partial Differential Equations. 20th International Conference on Information Fusion (Fusion), 2017. [本文引用:1]
[22]	Li H, Wu X J, Durrani T S. Infrared Physics & Technology, 2019, 102: 103039. [本文引用:1]
[23]	Zhang Y, Zhang L J, Bai X Z. Infrared Physics & Technology, 2017, 83: 227. [本文引用:1]
[24]	Bavirisetti D P, Dhuli R. Infrared Physics & Technology, 2016, 76: 52. [本文引用:1]
[25]	Chibani Y. Isprs Journal of Photogrammetry & Remote Sensing, 2006, 60(5): 306. [本文引用:1]
[26]	Xydeas C S, Petrovic V. Objective Image Fusion Performance Measure, IEEE Xplore, 2000, doi: DOI:10.1049/el:20000267. [本文引用:1]
[27]	Chen Yin, Blum R S. Image & Vision Computing, 2009, 27(10): 1421. [本文引用:1]
[28]	Qu G, Zhang D, Yan P. Electronics Letters, 2002, 38(7): 313. [本文引用:1]
[29]	Wang Qiang, Shen Y, Jin J. Image Fusion, 2008, 19: 469. [本文引用:1]
[30]	Yang C, Zhang J Q, Wang X R, et al. Information Fusion, 2008, 9(2): 156. [本文引用:1]

2021

0.0

... 然而, 随着战场实际需要的多样化及复杂化, 单一成像传感器受限于自身的物理成像原理, 只能感知部分目标或战场信息, 很难完成多种目标背景下的探测和识别任务^[1] ...

2020

0.0

... 因此, 通过融合多种传感器图像数据以实现不同传感器数据之间的互补, 可以得到更加直观、可靠和全面的目标或场景, 进而为后续特征提取、目标识别和检测等任务提供强有力的数据支持, 便于做出更加合理的决策^[2] ...

2001

0.0

... 图像融合大多是在像素级进行研究, 其中, 依据图像表示和融合过程的不同, 图像融合大致可以分为四类: 基于空间域的方法^[3], 基于变换域的方法^[4], 基于神经网络的方法^[5]和基于字典学习的方法^[6] ...

2014

0.0

2015

0.0

2012

0.0

2006

0.0