硅漂移探测器中逃逸峰的分析与计算

引用本文

廖学亮, 刘明博, 程大伟, 沈学静. 硅漂移探测器中逃逸峰的分析与计算[J]. 光谱学与光谱分析, 2024,44(5): 1297-1300.
LIAO Xue-liang, LIU Ming-bo, CHENG Da-wei, SHEN Xue-jing. Analysis and Calculation of Escape Peaks in Silicon Drift Detectors[J]. Spectroscopy and Spectral Analysis, 2024,44(5): 1297-1300.
Doi:10.3964/j.issn.1000-0593(2024)05-1297-04 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

硅漂移探测器中逃逸峰的分析与计算

廖学亮, 刘明博, 程大伟, 沈学静

钢研纳克检测技术股份有限公司, 北京 100094

作者简介: 廖学亮, 1988年生, 钢研纳克检测技术股份有限公司硕士研究生 e-mail: 851661195@qq.com

收稿日期: 2022-08-11 修订日期: 2023-08-25

基金: 国家重点研发计划项目(2021YFC2903100)资助

摘要

能量色散X射线荧光光谱所使用的硅漂移探测器(SDD)在检测过程中会在个别含量较高待测元素所产生的较强特征峰的低能侧形成逃逸峰, 其相应的特征峰也会损失一部分强度, 逃逸峰的产生位置与探测器的成分有关; SDD探测器中入射特征峰与逃逸峰之间的能量差值为1.739 keV, 等于硅原子的 K_α特征能量, 逃逸峰的强度与入射X射线的强度成正比, 即与相应元素的含量/特征峰强度成正比, 通常的入射特征峰逃逸概率比较低, 在逃逸峰强度较低时对测试结果影响较小, 当基体元素含量较高时产生的逃逸峰较大就会导致测试结果偏差较大; 通过理论计算可以看出, 逃逸峰的产生概率与探测器角度及元素种类等条件有关, 从硅原子的质量吸收系数的变化趋势可以发现, 随着入射特征线能量的增大硅原子对其的质量吸收系数降低, 相应入射线的逃逸峰产生概率也会降低。当逃逸峰与其他待测元素的特征能量峰位置有重合时, 会干扰相应元素的准确测量, 导致相应元素的特征峰强度偏大, 尤其是当待测元素含量较低时, 其产生的特征峰强度较小, 逃逸峰导致的本底强度所产生的干扰相对更大, 因此需要对逃逸峰进行准确计算和校正。搭建了相应的平台进行测试, 并以Fe和Mn元素为例, 通过对SDD探测器中两种元素产生的逃逸峰概率进行理论分析与计算, 并与实际测试谱图得到的逃逸概率值进行对比, 发现两种数据符合较好, 并且经对比发现在Fe₂O₃样品中的Fe∶ K_β线的逃逸峰与Cr∶ K_α峰重合, Fe∶ K_α线的逃逸峰与Ti∶ K_α峰有部分重合, 在扣去逃逸峰后可以降低检出限, 以更好地对Cr和Ti进行准确定量, 该方法可扩展到其他含量较高元素的逃逸峰计算与校正, 尤其是在土壤、矿物、合金检测等个别元素含量较高的样品中多元素检测方面的应用, 可提高X射线荧光方法的测试准确度。

关键词: 逃逸峰; 能量色散X射线荧光光谱法; 硅漂移探测器

中图分类号:O582 文献标志码:A

Analysis and Calculation of Escape Peaks in Silicon Drift Detectors

LIAO Xue-liang, LIU Ming-bo, CHENG Da-wei, SHEN Xue-jing

NCS Testing Technology Co., Ltd., Beijing 100094, China

Abstract

During the detection process, the silicon drift detector (SDD) used in energy-dispersive X-ray fluorescence spectrometry will form escape peaks on the low-energy side of the solid characteristic peaks generated by the individual elements to be measured with high content, and the corresponding characteristic peaks are also will lose some strength, and the location of the escape peak is related to the composition of the detector. The energy difference between the incident characteristic peak and the escape peak in the SDD detector is 1.739 keV, which is equal to the K_α characteristic energy of the silicon element. The intensity of the escape peak is proportional to the intensity of the incident X-ray, that is, proportional to the content of the corresponding element/characteristic peak intensity. The escape probability of the incident characteristic peak is usually low, and the influence on the test results is small when the escape peak intensity is low. It can be seen from theoretical calculations that the probability of generating escape peaks is related to the detector angle and element types, and with the increase of the incident characteristic line energy, the mass absorption coefficient of the silicon atom and the corresponding escape peak generation probability will also reduce. When the escape peak coincides with the characteristic energy peaks of other elements to be measured, it will interfere with the accurate measurement of the corresponding element, especially when the content of the element to be measured is low. The interference will be relatively more significant. Therefore, it is necessary to calculate and correct the escape peak accurately. In this paper, a corresponding platform is built for testing, and taking Fe and Mn elements as examples, through theoretical analysis and calculation of the escape peak probability in the SDD detector and compared with the escape probability value obtained from the actual test spectrum, it is found that the two data are in good agreement, and after the comparison it was found that the escape peak of Fe∶ K_β line in Fe₂O₃ sample overlapped with Cr∶ K_α peak, and the escape peak of Fe∶ K_α line partially overlapped with Ti∶ K_α peak. After deducting the escape peak, Cr and Ti can be better analyzed for accurate quantification. This method can be extended to the calculation and correction of escape peaks of other elements with higher content, especially in the application of multi-element detection in samples with high content of individual elements such as soil, mineral, alloy detection, etc, and improve the test accuracy of X-ray fluorescence method.

Keyword: Escape peak; Energy-dispersive X-ray fluorescence (EDXRF); Silicon drift detector

文章图片

引言

能量色散X射线荧光光谱仪是一种使用比较广泛的设备, 探测器作为核心部件常用的类型有Si-PIN和硅漂移(SDD)两种, 都是以硅为主要成分构成。以硅漂移探测器为例, 在进行检测时, 当高于硅原子K_α特征吸收限能量的X射线照射到探测器, 会激发硅原子产生K_α特征谱线, 其中一部分特征谱线逃逸出硅晶体表面, 未转化成脉冲信号而在入射线的低能侧形成逃逸峰, 两个峰之间的能量差值等于硅原子的K_α特征能量, 逃逸峰强度与入射X射线强度成正比, 即与相应元素的含量即特征峰强度成正比, 这种现象在待测元素含量比较高, 特征峰较强的情况下比较常见。当逃逸峰的位置与其他待测元素位置完全重合或部分重合时, 会对待测元素谱峰强度产生干扰, 如果计算处理不当, 就无法得出正确的待测元素的含量。

能量色散X射线荧光光谱技术在土壤、矿物、合金检测等方面应用广泛, 当基体中个别元素的含量比较高时, 其在测试过程中由于峰强度较大, 会产生一定比率的逃逸峰, 本文将以Fe、 Mn这两种元素为例进行计算和比对。

1 原理与方法

硅漂移探测器(SDD)在探测过程中, 本征层吸收X射线光子后发生光电离, 并产生相应数量的载流子(电子-空穴对), 电子在电场的作用下漂移到阳极区被收集产生电流, 理想情况下探测器应能收集每一入射光子产生的电荷, 电荷总数对应光子能量^[1]。只有被有效并完全收集的信号才能正确地反映相应元素的含量。然而在实际检测过程中因探测器探测效率、逃逸峰、合峰等导致有些待测元素峰强度与含量的比例有所偏差, 通常在同样入射峰强度条件下所产生的逃逸峰的强度比合峰大很多, 因此逃逸峰对其所在位置的待测元素的干扰更大, 需要进行校正。

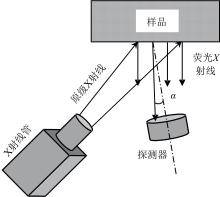
当一束X射线光子照射到探测器时, 取深度x处dx厚的单位体积硅固体体积元Q作为最小单元(如图1所示), 体积元内发生光电效应而形成的入射线总计数(包含逃逸峰) ${N_{I}}^{[2]}$ 为式(1)

$d N_{I} = I_{0} e^{- μ_{1} ρx} μ_{τ} ρ d x (1)$

	Figure Option View Download New Window
	图1 激发及逃逸光子路径示意图Fig.1 Schematic diagram of the excitation and escape photon paths

入射线光电效应总计数(包括逃逸峰)为式(2)

$N_{I} = \int_{x}^{=} I_{0} μ_{τ} ρ e^{- μ_{1} ρx} d x = \frac{I_{0} μ_{τ}}{μ_{1}}$ (2)

当入射线光子能量大于硅原子K_α的吸收限1.839 keV时, 会激发其产生K_α: 1.739 keV光子, 这部分光子由于本体材料硅对其吸收效率低^[3], 有一部分逃逸出探测器的端面从而使入射线光子损失1.739 keV能量, 在低能侧形成一个峰。 I₀为入射线强度(光子· cm^-2· s), 在单位时间内, 体积元内产生的硅的K_α光子数为 $d {N_{P}}^{[2]}$ 为式(3)

$d N_{p} = I_{0} e^{- μ_{1} ρx} μ_{τ} ωg \frac{γ - 1}{γ} ρ d x$ (3)

这些光子中, 逃逸出硅探测器端面的路径区域为锥形结构, 其相对立体角为式(4)

$d Ω = \int_{φ}^{=} \frac{r \sin θ d θr d φ}{4 π r^{2}} = \frac{1}{2} \sin θ d θ$ (4)

逃逸出硅探测器端面的光子数 $d {N_{e}}^{[2]}$ 为式(5)

$d N_{e} = d N_{p} \frac{1}{2} \sin θ e^{- μ_{0} ρ \frac{x}{\cos θ}} d θ$ (5)

式(5)中, μ ₀为硅的K_α光子在硅中的总吸收系数; μ ₁为入射线在硅中的总质量吸收系数; μ _τ为如射线在硅中的光电效应吸收系数; γ 为如射线在硅中的K吸收限跃迁比; ω 为硅K系X射线荧光产额; g为硅K_α分支比; ρ 为硅的密度。

逃逸峰总计数 ${N_{e}}^{[4]}$ 为式(6)

$\begin{array}{l} N_{e} = \frac{1}{2} I_{0} μ_{τ} ωg \frac{γ - 1}{γ} ρ \int_{θ}^{=} \int_{x}^{=} e^{- μ_{1} ρx} e^{- μ_{0} ρ \frac{x}{\cos θ}} \sin θ d x d θ \\ = \frac{1}{2} I_{0} μ_{τ} ωg \frac{γ - 1}{γ} [\frac{1}{μ_{1}} - \frac{μ_{0}}{μ_{1}^{2}} \ln (1 + \frac{μ_{1}}{μ_{0}})] \end{array}$ (6)

逃逸峰N_e与总计数峰N_I两者之比为式(7)

$\frac{N_{e}}{N_{I}} = \frac{1}{2} ωg \frac{γ - 1}{γ} [1 - \frac{μ_{0}}{μ_{1}} \ln (1 + \frac{μ_{1}}{μ_{0}})]$ (7)

2 计算实例

在实际测试平台中由于结构空间限制, 为了让探测器接收更多的射线, 探测器会旋转一定角度让其中轴线对准激发区域的中心而不是垂直于样品下表面[如图2(a)], 因此经原级X射线激发产生的荧光光谱在经过准直以后会以一定的角度进入探测器, 将样品出射的线简化为平行向下的线束, 其方向与探测器的中轴线角度为α , 如图2(b)所示。

	Figure Option View Download New Window
	图2 测试平台角度(a)及入射线进入探测器路径(b)Fig.2 The angle of the test platform (a) and the path of the incident ray entering the detector (b)

逃逸出硅探测器端面的光子路径根据实际情况由xcosθ 修正为xcosα /cosθ , 实测角度α 约为4° , 逃逸光子数为 $d {N_{e}}^{[5]}$ 为

$d N_{e} = d N_{p} \frac{1}{2} \sin θ e^{- μ_{0} ρ \frac{x \cos α}{\cos θ}} d θ$ (8)

使用式(8)替代式(5)并代入式(6)并重新计算逃逸概率, 见式(9)

$P = \frac{N_{e}}{N_{I}} = \frac{1}{2} ωg \frac{γ - 1}{γ} [1 - \frac{μ_{0} \cos α}{μ_{1}} \ln (1 + \frac{μ_{1}}{μ_{0} \cos α})]$ (9)

在实际测试时由于得到的待测元素峰中不包含逃逸峰, 因此实测峰与逃逸峰的比例为式(10)

$R = \frac{P}{1 - P}$ (10)

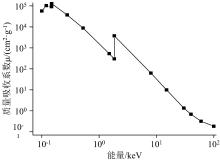
通过查表可以得到数据^{[6, 7]}: ω =0.055, γ =11.89, g=0.974; 质量吸收系数采用de Boer算法中的数据^[6], 通过数据插值得到Si在不同能量位置的质量吸收系数, 用于插值的数据如图3所示。

	Figure Option View Download New Window
	图3 Si对不同能量射线的质量吸收系数Fig.3 Mass absorption coefficient of Si to different energy rays

分别采用纯MnO₂与Fe₂O₃作为实际样品在测试平台上进行测试, 通过计算式(9)可以看出, 逃逸比例与管压管流无关, 因此为了得到不同强度下的逃逸峰强度, 采用26、 28、 30、 32、 34、 36、 38和40 kV管压进行激发测试, 并在扣除背景情况下分别统计出Mn和Fe的K_α峰强度、 K_α逃逸峰强度、 K_β峰强度、 K_β逃逸峰强度, 如图4所示。

	Figure Option View Download New Window
	图4 逃逸峰与主峰强度相关性 (a): Mn: K_α; (b): Mn: K_β; (c): Fe: K_α; (d): Fe: K_βFig.4 Correlation between the escape peak of different elements and the intensity of their main peaks (a): Mn: K_α; (b): Mn: K_β; (c): Fe: K_α; (d): Fe: K_β

图4(a—d)四条曲线斜率十分接近逃逸峰强度与峰强度之比, 如表1中实测值通过与理论计算数据对比, Mn的K_α和K_β峰, 以及Fe的K_α峰逃逸概率符合地较好, Fe的K_β峰的逃逸概率差异较大, 对谱图进行分析, Fe的K_β的逃逸峰5.320 keV与Cr的K_α: 5.415 keV峰有重合, 探测器的分辨率不足以将其分开, 过高的逃逸峰说明样品中还含有一定量的Cr元素, 在这种情况下逃逸峰会对待测元素产生干扰, 因此对逃逸峰的准确计算有助于提高对其他待测元素的测试准确度。

表1 不同入射线的理论逃逸概率与实际测试值比对 Table 1 Comparison of theoretical escape probability and actual test value of different incident rays

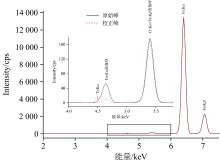
根据理论计算的逃逸峰概率, 对实际峰进行校正扣除, 可以很好地降低逃逸峰对待测元素的影响, 在图5样品中Cr∶ K_α峰面积由865 cps校正为为828 cps, Ti∶ K_α处的背景降到接近基线位置, 在提高待测元素的定量准确度和降低检出限方面具有一定的帮助。

	Figure Option View Download New Window
	图5 逃逸峰校正Fig.5 Escape peak correction

3 结论

通过对SDD探测器中逃逸峰概率的理论计算并与实际测试峰进行对比, 发现两种结果符合较好, 由于有些逃逸峰与待测元素的能量位置有重合, 会影响相应元素的测量, 以Fe和Mn元素为例, 经对比发现在Fe₂O₃样品中的K_β线的逃逸峰与Cr∶ K_α峰重合, K_α线的逃逸峰与Ti∶ K_α峰有部分重合, 在扣去逃逸峰以后才能对Cr和Ti进行准确定量, 方法可以应用于Fe元素含量较高且需要测试Cr和Ti元素的土壤、矿物及铁基合金中的样品中, 上述可扩展到其他含量较高的元素的逃逸峰计算与校正中, 提高仪器设备的测试准确度。

参考文献

文献列表

[1]	JI Ang, ZHUO Shang-jun, LI Guo-hui (吉昂, 卓尚军, 李国会). Energy Dispersive X-Ray Fluorescence Spectroscopy(能量色散X射线荧光光谱). Beijing: China Science Publishing & Media Ltd. (北京: 科学出版社), 2011. 86. [本文引用:1]
[2]	XIE Dong, YAN Zhen-zhuang(谢东, 严振庄). Nuclear Electronics & Detection Technology(核电子学与探测技术), 1992, 12(1): 35. [本文引用:1]
[3]	LIU Chun-lan(柳春兰). Physical Testing and Chemical Analysis(Part A: Physical Testing)(理化检验: 物理分册), 1982, 18(3): 18. [本文引用:1]
[4]	Reed S J B, Ware N G. Journal of Physics E: Scientific Instruments, 1972, 5(6): 582. [本文引用:1]
[5]	XIE Dong, YAN Zhen-zhuang, ZHANG Li-hua, et al(谢东, 严振庄, 张礼华, 等). Nuclear Electronics & Detection Technology(核电子学与探测技术), 1992, (6): 347. [本文引用:1]
[6]	ZHUO Shang-jun, TAO Guang-yi, HAN Xiao-yuan(卓尚军, 陶光仪, 韩小元). Fundamental Parameters of X-Ray Fluorescence Spectroscopy(X射线荧光光谱的基本参数法). Shanghai: Shanghai Scientific & Technical Publishers(上海: 上海科学技术出版社), 2010366, 379, 325. [本文引用:2]
[7]	LIU Yun-zuo(刘运祚). Commonly Used Radionuclide Decay Diagram(常用放射性核素衰变纲图). Beijing: Atomic Energy Press(北京: 原子能出版社), 1982. 406. [本文引用:1]