基于非对称多项式拟合的光谱波纹系数算法

引用本文

孙胜琳, 徐宏杰, 杨晟旻, 方佳豪, 梁佳辉. 基于非对称多项式拟合的光谱波纹系数算法[J]. 光谱学与光谱分析, 2024,44(5): 1283-1290.
SUN Sheng-lin, XU Hong-jie, YANG Sheng-min, FANG Jia-hao, LIANG Jia-hui. Spectral Ripple Algorithm Based on Asymmetric Polynomial Fitting[J]. Spectroscopy and Spectral Analysis, 2024,44(5): 1283-1290.
Doi:10.3964/j.issn.1000-0593(2024)05-1283-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于非对称多项式拟合的光谱波纹系数算法

孙胜琳, 徐宏杰, 杨晟旻, 方佳豪, 梁佳辉

北京航空航天大学仪器科学与光电工程学院, 北京 100191

作者简介: 孙胜琳, 女, 1998年生, 北京航空航天大学仪器科学与光电工程学院硕士研究生 e-mail: sdsunshenglin@163.com

收稿日期: 2022-08-26 修订日期: 2023-09-08

基金: 国家自然科学基金项目(61935002), 国防科技重点实验室基金项目(2021-JCJQ-LB-070-23)资助

摘要

在光纤陀螺中, 常采用超辐射发光二极管(SLD)或放大自发辐射(ASE)光源, 其较宽的光谱可有效抑制偏振噪声及背向反射、瑞利散射等影响。在SLD及ASE光源中, 波纹系数是一项重要指标, 其主要来自于宽带光源中未完全抑制掉的激射部分, 会对光纤陀螺的精度产生影响。目前在国军标中对波纹系数的定义是: 光谱曲线峰值波长附近的模式幅值的极差, 单位为dB。目前对波纹系数还是采用人眼观察的方法, 人眼观察具有一定的主观性和偶然性, 不能排除人们主观因素以及外界干扰带来的测量误差, 并且经过处理后得到的对数光谱不能准确反映原始光谱特性。针对宽带光源非对称光谱中的波纹系数进行分析, 对比多峰高斯拟合和多项式拟合各自的优缺点, 选择多项式拟合的方式; 通过理论分析及实验验证, 采用五次多项式拟合满足要求。基于三倍标准差原理提出了一种新的波纹系数计算方法, 可以准确反映波纹系数大小。采用AQ6370D光谱仪和自制的“光谱波纹系数测试”软件对ASE光源和SLD光源进行实验, 计算结果与人眼观察数据基本吻合。在此基础上进行重复性验证实验, 采集同一光源的五次实验数据, 分别计算其波纹系数, 并与人眼观察结果比较, 结果表明人眼观察只能估算到小数点后两位, 而光谱波纹系数算法精度较高, 分辨率可达0.000 1。自制的“光谱波纹系数测试”软件可以在交互界面上得到测试光谱的平均波长、峰值波长、中心波长、谱宽、波纹系数、线性坐标和对数坐标下的光谱及其拟合曲线表达式, 使实验分析更加方便快捷, 大大提高了实验效率。提出的基于非对称多项式拟合的光谱波纹系数算法可以更有效地对光源波纹系数进行判断, 提高了计算效率, 消除了主观性和偶然性的影响, 对国军标进行了补充, 有较为广阔的应用前景。

关键词: 波纹系数; 多项式拟合; 光谱拟合; 光源

中图分类号:Q433.5+9 文献标志码:A

Spectral Ripple Algorithm Based on Asymmetric Polynomial Fitting

SUN Sheng-lin, XU Hong-jie, YANG Sheng-min, FANG Jia-hao, LIANG Jia-hui

School of Instrumentation and Optoelectronic Engineering, Beihang University, Beijing 100191, China

Abstract

Super luminescent diode (SLD) and amplified spontaneous emission (ASE) light sources are often used in fiber optic gyroscopes. Their wide spectrum can effectively suppress the influence of polarization noise, back reflection and Rayleigh scattering. Ripple, as an important index in SLD and ASE light sources, mainly coming from the laser part of broadband light source that is not completely suppressed, impacts the accuracy of fiber optic gyroscope. In the military standard, ripple is defined as the range of mode amplitude near the peak wavelength of the spectral curve, with dB as the unit. At present, ripple measurement is mainly based on the logarithmic spectrum observed by human eyes. However, in human eye observation, the subjective factors of a human and the external interference may lead to subjectivity and contingency of the results, and measurement errors cannot be ruled out. Additionally, the spectrum in logarithmic coordinates cannot accurately reflect the spectral characteristics. Because of this, the present study analyzed the ripple in the asymmetric spectrum of the broadband light source, compared the advantages and disadvantages of multi-peak Gaussian fitting and polynomial fitting. Finally, adopted the polynomial fitting method. Through theoretical analysis and experimental verification, it was revealed that the quintic polynomial fitting can meet the requirements. Besides, a new method which can precisely calculate the ripple based on the triple standard deviation principle was proposed. AQ6370D spectrometer and a self-made “Spectral Ripple Fitting” software were utilized to experiment with ASE and SLD light sources, and the results obtained were in good agreement with the observation data of human eyes. On this basis, repeated validation experiments were carried out, the five experimental data of the same light source were recorded, and their ripple coefficients were calculated respectively. Compared with the human eye observation results, the experimental results demonstrate that the spectral ripple coefficient algorithm can well eliminate the influence of subjectivity and contingency, indicating that it is feasible. With the self-made “Spectral ripple Test” software, the average wavelength, peak wavelength, center wavelength, spectral width, ripple, linear coordinates and logarithmic coordinates of the spectrum and their fitting curve expressions can be obtained on the interactive interface, which makes the experimental analysis more convenient and speedy, thus significantly improving the experimental efficiency. It has been proved that the spectral ripple algorithm based on asymmetric polynomial fitting proposed in this paper can effectively judge the light source ripple, improve the calculation efficiency, and eliminate the influence of subjectivity and contingency, showing a broad application prospect. Furthermore, it is a supplement to the national military standard as well.

Keyword: Ripple; Polynomial fitting; Spectral fitting; Light source

文章图片

引言

超辐射发光二极管(super luminescent diode, SLD)或放大自发辐射(amplified spontaneous emission, ASE)光源光谱中都存在一定的光谱波纹系数, 主要来自于宽带光源中未完全抑制掉的激射部分。在光纤陀螺中, 波纹系数将会显著增加光源的相干时间, 从而增大Kerr效应、背向反射、 Rayleigh背向散射等诸多效应的影响, 从而使陀螺产生零偏的波动, 影响系统精度^{[1, 2]}。

目前对波纹系数的测量主要还是采用人眼观察的方法, 观察对数坐标下测出光谱曲线上峰值波长与邻近极小值的差。光谱波纹系数曲线如图1所示。人眼观察具有一定的主观性和偶然性, 不能排除人们主观因素以及外界干扰带来的测量误差, 并且经过处理后得到的对数光谱不能准确反映原始光谱特性。

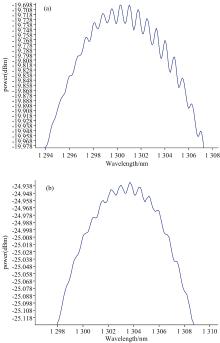	Figure Option View Download New Window
	图1 光谱波纹系数曲线 (a): SLD光源; (b): ASE光源Fig.1 Spectral ripple curve (a): SLD light source; (b): ASE light source

本文针对非对称光谱中的波纹系数进行分析, 对比高斯拟合和多项式拟合各自的优缺点, 选择多项式拟合的方式。通过理论分析和实验验证, 采用五次多项式拟合的波纹系数算法满足要求, 并设计开发光谱波纹系数测试软件, 通过导入光谱数据可自动计算出波纹系数大小。对SLD光源和ASE光源进行了实验并与人眼观察结果比较, 结果表明人眼观察只能估算到小数点后两位, 而光谱波纹系数算法精度较高, 分辨率可达0.000 1。

1 光谱波纹系数算法

1.1 波纹系数拟合算法的比较

多峰高斯拟合与多项式拟合都可以对非对称光谱曲线进行拟合。多峰高斯拟合精度相对更高, 但算法复杂, 以多峰(4peaks)高斯拟合为例, 需要计算12个参数, 其拟合公式为

$\begin{array}{l} y_{gauss} = a_{1} \exp (- {(\frac{x - b_{1}}{c_{1}})}^{2}) + a_{2} \exp (- {(\frac{x - b_{2}}{c_{2}})}^{2}) + \\ a_{3} \exp (- {(\frac{x - b_{3}}{c_{3}})}^{2}) + a_{4} \exp (- {(\frac{x - b_{4}}{c_{4}})}^{2}) \end{array}$ (1)

多项式拟合算法简单, 以五次多项式为例, 只需要6个参数, 并且在一定范围内精度与高斯拟合相差不大, 满足光谱波纹系数的计算要求。因此, 我们采用多项式拟合的方法计算非对称光谱波纹系数。五次多项式拟合公式为

$y_{polynomial} = a_{5} x^{5} + a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ (2)

ASE光源的多峰(4peaks)高斯拟合曲线和五次多项式拟合曲线如图2所示, 多峰高斯拟合数据的均方根误差为0.000 107 58, 五次多项式拟合数据的均方根误差为0.000 168 68, 在一定范围内精度满足光谱波纹系数的计算要求。

	Figure Option View Download New Window
	图2 ASE光源多峰高斯拟合曲线和多项式拟合曲线Fig.2 ASE light multi-peak gauss fitting curve and polynomial fitting curve

1.2 多项式拟合区间的选择

由于光谱中间部分的波纹系数对光源相干性影响较大而光谱边缘部分对相干性影响较小, 因此我们对线性坐标下中心波长周围的光谱曲线进行拟合来计算波纹系数的大小。由于区间过大不满足多项式分布, 区间过小又不够真实, 因此拟合区间的选取尤为重要。

半峰全宽(FWHM)指色谱峰高一半处的峰宽度, 即通过峰高的中点作平行于峰底的直线, 此直线与峰两侧相交两点之间的距离。由于不同光源的FWHM不同, 因此我们计算波纹系数时考虑FWHM对拟合区间的影响, 一般选取中心波长附近0.6倍的FWHM作为拟合区间。

1.3 光谱波纹系数算法

根据光谱特性, 本文提出了基于最小二乘法的五次多项式拟合的波纹系数算法, 通过比较原始数据和拟合数据的关系得到光谱波纹系数大小。实验中得到线性坐标光谱曲线由离散的点组成, 设离散数据点集为(x_i, y_i)(i=1, 2, …, n), 用曲线拟合的方法寻找y=f(x)的一个近似表达式y=p(x)。设拟合多项式为

$y = p (x) = a_{5} x^{5} + a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ (3)

根据最小二乘法定义, 通过给定的数据集(x_i, y_i)(i=1, 2, …, n)确定系数a_j(j=0, 1, 2, 3, 4, 5)使偏差平方和V(a₀, a₁, a₂, a₃, a₄, a₅)最小, 其表达式为

$\begin{array}{l} V (a_{0}, a_{1}, a_{2}, a_{3}, a_{4}, a_{5}) = \\ \overset{n}{\sum_{i = 1}} (a_{5} x_{i}^{5} + a_{4} x_{i}^{4} + a_{3} x_{i}^{3} + a_{2} x_{i}^{2} + a_{1} x_{i} + a_{0} - y_{i})^{2} \end{array}$ (4)

为了求得符合标准的a_j(j=0, 1, 2, 3, 4, 5)值, 对式(2)两边求a_j的偏导数并表示为矩阵XA=Y的形式

$\begin{array}{l} [\begin{array}{l} n & \overset{n}{\sum_{i = 1}} x_{i} & \overset{n}{\sum_{i = 1}} x_{i}^{2} & \overset{n}{\sum_{i = 1}} x_{i}^{3} & \overset{n}{\sum_{i = 1}} x_{i}^{4} & \overset{n}{\sum_{i = 1}} x_{i}^{5} \\ \overset{n}{\sum_{i = 1}} x_{i} & \overset{n}{\sum_{i = 1}} x_{i}^{2} & \overset{n}{\sum_{i = 1}} x_{i}^{3} & \overset{n}{\sum_{i = 1}} x_{i}^{4} & \overset{n}{\sum_{i = 1}} x_{i}^{5} & \overset{n}{\sum_{i = 1}} x_{i}^{6} \\ \overset{n}{\sum_{i = 1}} x_{i}^{2} & \overset{n}{\sum_{i = 1}} x_{i}^{3} & \overset{n}{\sum_{i = 1}} x_{i}^{4} & \overset{n}{\sum_{i = 1}} x_{i}^{5} & \overset{n}{\sum_{i = 1}} x_{i}^{6} & \overset{n}{\sum_{i = 1}} x_{i}^{7} \\ \overset{n}{\sum_{i = 1}} x_{i}^{3} & \overset{n}{\sum_{i = 1}} x_{i}^{4} & \overset{n}{\sum_{i = 1}} x_{i}^{5} & \overset{n}{\sum_{i = 1}} x_{i}^{6} & \overset{n}{\sum_{i = 1}} x_{i}^{7} & \overset{n}{\sum_{i = 1}} x_{i}^{8} \\ \overset{n}{\sum_{i = 1}} x_{i}^{4} & \overset{n}{\sum_{i = 1}} x_{i}^{5} & \overset{n}{\sum_{i = 1}} x_{i}^{6} & \overset{n}{\sum_{i = 1}} x_{i}^{7} & \overset{n}{\sum_{i = 1}} x_{i}^{8} & \overset{n}{\sum_{i = 1}} x_{i}^{9} \\ \overset{n}{\sum_{i = 1}} x_{i}^{5} & \overset{n}{\sum_{i = 1}} x_{i}^{6} & \overset{n}{\sum_{i = 1}} x_{i}^{7} & \overset{n}{\sum_{i = 1}} x_{i}^{8} & \overset{n}{\sum_{i = 1}} x_{i}^{9} & \overset{n}{\sum_{i = 1}} x_{i}^{10} \end{array}] \cdot \\ [\begin{array}{l} a_{0} \\ a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ a_{5} \end{array}] = [\begin{array}{l} \overset{n}{\sum_{i = 1}} y_{i} \\ \overset{n}{\sum_{i = 1}} x_{i} y_{i} \\ \overset{n}{\sum_{i = 1}} x_{i}^{2} y_{i} \\ \overset{n}{\sum_{i = 1}} x_{i}^{3} y_{i} \\ \overset{n}{\sum_{i = 1}} x_{i}^{4} y_{i} \\ \overset{n}{\sum_{i = 1}} x_{i}^{5} y_{i} \end{array}] \end{array}$ (5)

在数据量较大时直接使用正规方程组求解高阶多项式可能将问题转化为一个病态的方程, 因此本文采用QR分解法求解最小二乘问题, 对X进行QR分解, 分解为正交矩阵Q和上三角矩阵R, 得到多项式拟合系数A为

$A = R^{- 1} Q^{T} Y$ (6)

因此我们可以得到光谱波纹系数的拟合曲线y=p(x)=a₅x⁵+a₄x⁴+a₃x³+a₂x²+a₁x+a₀^{[3, 4]}。

实际中经常使用的一个标准是某个数据与数据的平均值的偏差大于三倍标准差, 就认为该数据为异常数据。三倍标准差公式为

$3 σ = 3 \times \sqrt[]{\frac{\overset{N}{\sum_{i = 1}} (X_{i} {- μ)}^{2}}{N}}$ (7)

式(7)中, X_i为实验数据, μ 为数据的平均值, N为数据个数。基于三倍标准差原理, 本文提出一种波纹系数新的定义, 原始数据f(x)偏离拟合数据p(x)的距离的平均数的三倍。光谱波纹系数公式为

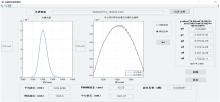
$Ripple = 3 \times \sqrt[]{\frac{\overset{n}{\sum_{i = 1}} [10 \lg (p (x)) - 10 \lg (f {(x))]}^{2}}{n}} (dB)$ (8)

2 实验结果与讨论

实验采用AQ6370D光谱仪和自制的“ 光谱波纹系数测试” 软件对SLD光源和ASE光源进行测试, 软件界面如图3所示, 包括光谱平均波长、峰值波长、中心波长、谱宽、波纹系数、线性坐标和对数坐标下的光谱及其拟合曲线表达式。在软件中导入光谱仪测得的实验数据, 可以自动计算出波纹系数大小。

	Figure Option View Download New Window
	图3 光谱波纹系数测试软件界面Fig.3 Spectral ripple testing software interface

2.1 ASE光源波纹系数计算

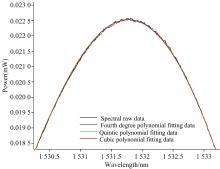
拟合ASE光源中心波长附近0.6倍FWHM的光谱波纹系数曲线, 目标函数选用了四次多项式、五次多项式和六次多项式三种算法进行拟合, 如图4所示。均方根误差计算结果如表1所示。可以看出, 四次多项式、五次多项式和六次多项式拟合曲线基本符合原始数据曲线的变化趋势, 四次多项式的均方根误差相对较大, 而五次多项式和六次多项式的均方根误差相差不大, 且六次多项式拟合较为复杂, 因此我们采用五次多项式拟合的方法计算波纹系数。

	Figure Option View Download New Window
	图4 ASE光源多项式拟合曲线Fig.4 ASE light source polynomial fitting curve

表1 ASE光源多项式拟合曲线的均方根误差 Table 1 The root mean square error of ASE light source polynomial fitting curve

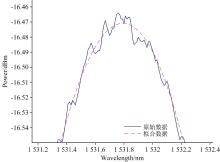
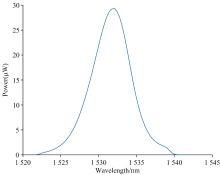
ASE光源光谱波纹系数五次多项式拟合曲线及计算结果如图5所示。根据式(8)计算得到波纹系数大小为0.011 649 2 dB, 将对数坐标下的光谱放大, 如图6所示, 通过人眼观察波纹系数大小约为0.02 dB, 与计算结果基本吻合。

	Figure Option View Download New Window
	图5 ASE光源光谱波纹系数测试结果Fig.5 The spectral ripple calculation results of ASE light source

	Figure Option View Download New Window
	图6 ASE光源对数坐标下的放大光谱Fig.6 ASE light source amplification spectrum in logarithmic coordinates

2.2 SLD光源波纹系数计算

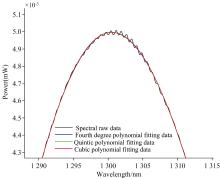
采用四次多项式、五次多项式和六次多项式三种算法, 分别对SLD光源中心波长附近0.6倍FWHM的光谱波纹系数曲线进行拟合, 如图7所示。均方根误差计算结果如表2所示。可以看出, 三种目标函数的拟合曲线基本符合原始数据曲线的变化趋势, 均方根误差相差不大, 为了和ASE光源统一算法, 我们采用五次多项式拟合的方法计算波纹系数。

	Figure Option View Download New Window
	图7 SLD光源多项式拟合曲线Fig.7 SLD light source polynomial fitting curve

表2 SLD光源多项式拟合曲线的均方根误差 Table 2 The root mean square error of SLD light source polynomial fitting curve

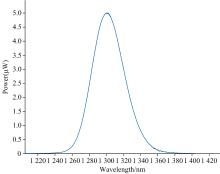
SLD光源光谱波纹系数五次多项式拟合曲线及计算结果如图8所示。根据式(8)计算得到波纹系数大小为0.020 929 1 dB, 将对数坐标下的光谱放大, 如图9所示, 通过人眼观察波纹系数大小约为0.02 dB, 与计算结果基本吻合。

	Figure Option View Download New Window
	图8 SLD光源光谱波纹系数测试结果Fig.8 The spectral ripple calculation results of SLD light source

	Figure Option View Download New Window
	图9 SLD光源对数坐标下的放大光谱Fig.9 SLD light source amplification spectrum in logarithmic coordinates

2.3 重复性验证实验

为了排除实验具有的偶然性, 我们对ASE光源和SLD光源进行重复性验证实验, 考察波纹系数算法的可行性。

2.3.1 ASE光源的重复性验证实验

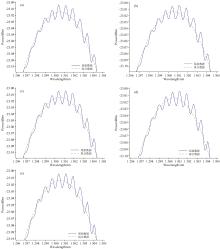
选取同一ASE光源进行五次实验, 测试其波纹系数并与人眼观察结果相比较, 实验所用光源光谱如图10所示, 对数坐标下的放大光谱如图11所示, 实验测得波纹系数如表3所示。

	Figure Option View Download New Window
	图10 实验所用ASE光源光谱Fig.10 Spectra of ASE light source used in the experiment

	Figure Option View Download New Window
	图11 实验所用ASE光源对数坐标下的放大光谱 (a): 测试1; (b): 测试2; (c): 测试3; (d): 测试4; (e): 测试5Fig.11 Amplified spectra of ASE light source used in the experiment in logarithmic coordinates (a): Test 1; (b): Test 2; (c): Test 3; (d): Test 4; (e): Test 5

表3 实验所用ASE光源波纹系数测试结果 Table 3 Test results of ripple of ASE light source used in the experiment

由表3可知, 受人们主观因素以及外界干扰的影响, 人眼观察的精度较低, 只能估算到小数点后两位; 用软件测试所得的波纹系数比较稳定, 消去了主观性和偶然性的影响, 精度较高, 分辨率可达0.000 1。

2.3.2 SLD光源的重复性验证实验

选取同一SLD光源进行五次实验, 测试其波纹系数并与人眼观察结果相比较, 实验所用光源光谱如图12所示, 对数坐标下的放大光谱如图13所示, 实验测得波纹系数如表4所示。

	Figure Option View Download New Window
	图12 实验所用SLD光源光谱Fig.12 Spectra of SLD light source used in the experiment

	Figure Option View Download New Window
	图13 实验所用SLD光源对数坐标下的放大光谱 (a): 测试1; (b): 测试2; (c): 测试3; (d): 测试4; (e): 测试5Fig.13 Amplified spectra of SLD light source used in the experiment in logarithmic coordinates (a): Test 1; (b): Test 2; (c): Test 3; (d): Test 4; (e): Test 5

表4 实验所用SLD光源波纹系数测试结果 Table 4 Test results of ripple of SLD light source used in the experiment

由表4可知, 受人们主观因素以及外界干扰的影响, 人眼观察的精度较低, 只能估算到小数点后两位; 用软件测试所得的波纹系数精度较高, 分辨率可达0.000 1。

根据以上重复性验证实验可知, 波纹系数算法可以很好地消除主观性和偶然性的影响, 具有可行性。

3 结论

提出了一种五次多项式拟合的光谱波纹系数算法, 并采用AQ6370D光谱仪和自制的“ 光谱波纹系数测试” 软件对ASE光源和SLD光源进行实验, 并与人眼观察结果比较, 结果表明人眼观察只能估算到小数点后两位, 而本文提出的算法分辨率可达0.000 1, 远远优于人眼观察法。自制的“ 光谱波纹系数测试” 软件可以在交互界面上得到测试光谱的平均波长、峰值波长、中心波长、谱宽、波纹系数、线性坐标和对数坐标下的光谱及其拟合曲线表达式, 使实验分析更加方便快捷, 大大提高了实验效率。本文提出的基于非对称多项式拟合的光谱波纹系数算法可以更有效地对光源波纹系数进行判断, 提高了计算效率, 消除了主观性和偶然性的影响, 对国军标进行了补充, 有较为广阔的应用前景。

参考文献

文献列表

[1]	WANG Wei(王巍). Interference Fiber Optic Gyroscope Technology(>干涉型光纤陀螺仪技术). Beijing: China Aerospace Publishing House(北京: 中国宇航出版社), 2010. [本文引用:1]
[2]	CHEN Yu, ZHANG Yao-qi, CHEN Qian(陈渝, 张耀麒, 陈倩). Semiconductor Optoelectronics(半导体光电), 2012, 33(2): 175. [本文引用:1]
[3]	LI Hai-xia, HAN Yun-long, HONG Min(李海霞, 韩云龙, 洪敏). Linear Algebra(线性代数). Xi'an: Northwest University of Technology Press(西安: 西北工业大学出版社), 2018. [本文引用:1]
[4]	GU Gui-ding, ZHANG Zhen-yu(顾桂定, 张振宇). Matrix Theory(>矩阵论). Shanghai: Shanghai University of Finance and Economics Press(上海: 上海财经大学出版社), 2017. [本文引用:1]