基于高光谱数据的纸张粘度反演模型构建

引用本文

王飒, 曲亮, 张立福, 高宇, 李广华, 常晶晶. 基于高光谱数据的纸张粘度反演模型构建[J]. 光谱学与光谱分析, 2024,44(12): 3524-3533.
WANG Sa, QU Liang, ZHANG Li-fu, GAO Yu, LI Guang-hua, CHANG Jing-jing. Research on the Inverse Model of Paper Viscosity Based on Hyperspectral Data[J]. Spectroscopy and Spectral Analysis, 2024,44(12): 3524-3533.
Doi:10.3964/j.issn.1000-0593(2024)12-3524-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于高光谱数据的纸张粘度反演模型构建

王飒^1,², 曲亮^1,^2,^*, 张立福³, 高宇³, 李广华^1,², 常晶晶^1,²

1.故宫博物院, 北京 100009

2.中国-希腊文物保护技术“一带一路”联合实验室, 北京 100009

3.中国科学院空天信息创新研究院, 北京 100101

*通讯作者 e-mail: quliang@dpm.org.cn

作者简介: 王飒, 1990年生, 故宫博物院博士后 e-mail: wangsa_01@yeah.net

收稿日期: 2023-11-14 修回日期: 2024-03-13

基金: 国家重点研发计划项目(2020YFE0204600), 北京故宫文物保护基金会和万科公益基金会专项经费资助

摘要

纸质文物对我国历史文化传承和民族精神延续具有重要意义, 而纸张老化严重损害了文物寿命。纸张粘度是反映纸张老化程度的重要指标, 传统粘度测量方法是一种有损的破坏性实验, 对珍贵文物造成不可避免的二次伤害。针对这一问题, 高光谱遥感技术能够实现无损快速分析, 是建立纸张粘度反演的有效途径。以干热和湿热纸张老化为研究对象, 获取了110组测定粘度含量的模拟纸张老化样本, 通过光谱滤波处理, 建立了纸张老化的高光谱数据库。在此基础上, 对比分析了原始光谱的一阶微分、二阶微分、倒数对数、倒数对数一阶微分以及多元散射校正、多元散射校正光谱一阶微分、多元散射校正光谱二阶微分、多元散射校正光谱倒数对数和连续小波变换9种数据处理方法, 将其与基于竞争自适应重加权采样算法(CARS)和相关系数法( R)组合作为模型的输入, 通过数据集划分验证优选出最优模型。研究结果表明: (1)原始光谱430 nm处光谱数据与粘度相关性最高, R为0.75, 经过原始光谱倒数对数一阶微分变换后, 430 nm处的 R为0.874, 显著增加了光谱中纸张粘度信息; (2)原始光谱二阶微分变换后, 578 nm处的相关性最高, R为0.57, 远低于原始光谱数据的最高 R(0.75), 说明二阶微分不适应于纸张粘度估算, 同时其他变换方法的最大相关系数均大于原始光谱, 表明了光谱变换的有效性; (3)对于原始光谱, 随着分解尺度的增加, 光谱中包含的纸质粘度信息有所减少, 最大相关系数出现在分解尺度2的484 nm处, 为0.873; (4)在不同的输入组合中, 原始光谱倒数对数一阶微分作为输入时的模型精度最高, 基于CARS方法的支持向量机回归(SVR)、随机森林(RF)和AdaBoost模型在验证数据集中的 R²分别为0.96、 0.93和0.93, RMSE分别为14.80、 18.33和19.79 mL·g^-1, 建议在纸张粘度反演中, 优先选择原始光谱倒数对数一阶微分作为输入, CARS特征选择算法的SVR模型。以上研究结论表明了高光谱技术在纸张粘度无损分析的适用性, 能够对纸质文物的修复工作提供科学依据。

关键词: 纸张粘度; 高光谱; 特征选择; 深度学习

中图分类号:TP79 文献标志码:A

Research on the Inverse Model of Paper Viscosity Based on Hyperspectral Data

WANG Sa^1,², QU Liang^1,^2,^*, ZHANG Li-fu³, GAO Yu³, LI Guang-hua^1,², CHANG Jing-jing^1,²

1. The Palace Museum, Beijing 100009, China

2. China-Greece Belt and Road Joint Laboratory on Cultural Heritage Conservation Technology, Beijing 100009, China

3. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China

*Corresponding author

Abstract

Paper-based cultural relics hold crucial significance to the historical and cultural heritage and the continuation of the national spirit in China. At the same time, the aging of paper seriously affects the longevity of artifacts. Paper viscosity is an important indicator reflecting the degree of paper aging. Traditional paper viscosity measurement methods are destructive experiments that cause inevitable secondary damage to valuable cultural relics. Hyperspectral remote sensing technology can achieve non-destructive and rapid analysis to address this issue, providing an effective approach to establishing a paper viscosity inversion model. In this study, drying and moist-heat paper aging were taken as the research subjects, and110 groups of simulated paper aging samples with measured viscosity content were obtained. Through spectral filtering, a hyperspectral database of paper aging was established. Based on this, nine data processing methods, including original spectrum first-order derivative, original spectrum second-order derivative, original spectrum reciprocal logarithm, original spectrum reciprocal logarithm first-order derivative, multiplicative scatter correction, multiplicative scatter correction spectrum first-order derivative, multiplicative scatter correction spectrum second-order derivative, multiplicative scatter correction spectrum reciprocal logarithm, and continuous wavelet transform were analyzed, as well as two feature selection methods, competitive adaptative reweighted sampling (CARS) and correlation coefficients ( R), were analyzed in combination as input for the models to identify the best model through dataset partitioning validation. Research results have shown: (1) In the original spectrum, the correlation at 430 nm is the highest with viscosity, with an R-value of 0.75. After data processing, the R-value at 430 nm increases to 0.874 following the application ofthe reciprocal logarithm first-order derivative of the original spectrum method, which significantly enhances the paper viscosity information in the spectrum; (2) After the original spectrum is transformed into the second-order derivative, the correlation at 578 nm is the highest, with an R-value of 0.57, significantly lower than the highest R-value (0.75) in the original spectral data. This finding indicates that the second-order derivative is unsuitable for paper viscosity estimation. Meanwhile, the maximum correlation coefficients of other transformation methods are all higher than the original spectrum, demonstrating the effectiveness of spectral transformation; (3) For the original spectrum, as the decomposition scale increases, the paper viscosity information contained in the spectrum decreases, and the highest correlation coefficient occurs at 484nm at the decomposition scale of 2, with a value of 0.873; (4) Among different input combinations, the model with the highest accuracy uses the reciprocal logarithm first-order derivative of the original spectrum as input. Based on the CARS method, the support vector regression (SVR),random forest (RF), and AdaBoost models have R² values of 0.96, 0.93, and 0.93, respectively, and RMSE values of 14.80, 18.33, and 19.79 mL·g^-1 for the validation dataset. We recommend prioritizing using the reciprocal logarithm first-order derivative of the original spectrum as inputs and the SVR model with the CARS feature selection algorithm for paper viscosity inversion. The above research findings demonstrate the applicability of hyperspectral technology for non-destructive analysis of paper viscosity, providing a scientific basis for the restoration work of paper-based cultural relics.

Keyword: Paper viscosity; Hyperspectral; Feature selection; Deep learning

文章图片

引言

纸质文物承载着我国历史文化的传承和民族精神的延续^[1], 具有重要的政治、经济、文化和科学价值。随着时间和环境的改变, 如环境的温度、湿度、霉变、光照和紫外等, 纸张会出现老化现象, 严重影响文物的寿命和艺术价值^[2], 因此研究纸张的性能十分必要。随着纸张的不断老化, 纤维素分子降解, 纤维素平均长度降低, 聚合度变小, 纸张粘度下降, 而纸张聚合度可以通过用粘度计算, 因此, 粘度作为研究纸张聚合度的重要指标而备受关注。目前关于纸张粘度的测量, 主要是依据GB/T1548—2004《纸浆粘度的测定》, 该方法测定前需要粉碎纸张配置化学溶液, 是一种有损的破坏性实验, 考虑到纸质文物极高的艺术和文化价值, 一般不能满足此要求, 因此亟需开展一种无损的纸张粘度估算新方法。

高光谱遥感技术起源于20世纪80年代初期^[3], 通过获取目标物体在可见光谱到近红外范围内的连续光谱信息来反映目标物的特性, 具有光谱分辨率高、图谱合一的独特优势, 经过近40年的飞速发展, 已广泛应用于农业、环境、食品和考古等领域^[4]。在文物保护与修复领域, 高光谱遥感能够避免文物的二次破坏, 通过对文物进行高光谱扫描, 从而发现肉眼难以分辨的隐藏信息。典型应用如颜料种类的分析与识别^{[5, 6, 7]}、隐藏信息提取以及修复痕迹的识别与提取^{[8, 9, 10, 11]}等。粘度作为纸张老化的重要指标, 已基于高光谱技术被进行了一定的研究, 如易晓辉等基于近红外光谱, 通过计算一阶导数和多元散射校正(multiplicative scatter correction, MSC)建立了纸张纤维聚合度的光谱反演模型, 证明了高光谱反演纸张老化参数的可行性^[12]; 高宇等的研究表明430 nm的光谱反射率与粘度的相关性较好, 从而提出了粘度指数来估算纸张粘度, 但是该方法在测试集中R²仅为0.76^[13], 反演精度较低, 因此, 亟需其他的高光谱纸张粘度反演模型来提高精度。

近年来, 由于计算能力的提升和获取数据便捷性的增加, 使得机器学习模型, 包括神经网络、遗传算法、支持向量机等算法可用于纸张性能的反演, 如李扬基于老化模拟分析软件和多层神经网络, 结合理化和环境因素等参数预测了8个纸张样本的使用寿命^[14]。深度学习模型能够捕捉遥感反射率和生物地球物理参数之间复杂的非线性关系, 基于迭代学习来减少总体误差并实现最大化模型拟合, 可为纸张粘度反演提供新的有效途径。

综上, 本研究通过实验室模拟纸张老化建立数据库, 结合高光谱技术和深度学习模型, 采用不同的高光谱数据处理算法和特征光谱选择算法, 优选出最佳的纸张粘度的反演模型, 从而为纸张粘度的无损估算提供实验参考, 对纸质文物的修复工作提供科学依据。

1 实验部分

1.1 样本与设备

纸张样本材质为红星棉料四尺单宣, 其中青檀皮和草料按照4: 6进行均匀混合, 并在恒温室模拟干热和湿热的纸张老化过程, 其中干热老化的胶矾水配比设置为3组, 分别为: 2%胶+1%矾、 2%胶+2%矾和2%胶+4%矾, 湿热老化的胶矾水配比设置为4组, 分别为: 2%胶+0%矾、 2%胶+1%矾、 2%胶+2%矾和2%胶+4%矾, 共计110个样本, 详见文献[13]。纸张粘度依据GB/T1548—2004《纸浆粘度的测定》测定, 共获取了110个粘度数据。

采用的高光谱采集仪器为HS-VN/SW2500CR, 光谱范围为400~2 500 nm, 可见光谱分辨率为1.6 nm, 共370个波段。

1.2 数据采集

通过高光谱仪对备制的纸张样本进行扫描, 获取了每个老化纸张样本的高光谱数据影像, 对影像中的纯净纸面部分进行裁剪, 去除其中存在非纸张和颜料部分, 保留仅含纯净纸张区域的影像, 并通过Savitzky-Golay(S-G)滤波进行去噪处理, 在此基础上计算每个纸张样本的光谱平均值, 以此作为纸张样本的原始光谱数据, 共获取了110组纸张原始光谱。由于元件噪声干扰, 导致采集光谱的首尾两端噪声信号过大、信噪比较低, 因此选择了425~977 nm的340个波段进行后续研究。

1.3 高光谱数据处理

高光谱数据在获取的过程中, 容易受到纸张表面平整度和环境因素的干扰影响, 为了减少和去除与纸张粘度含量无关的噪声信息, 进行以下的数据预处理。

1.3.1 多元散射校正

多元散射校正(MSC)能够有效消除不同散射水平的光谱差异, 从而提高数据的信噪比。计算过程如下:

假设有n条光谱数据R, 那么这n条光谱数据的平均值 $\overset{̅}{R}$ 为

$\overset{̅}{R} = \frac{1}{n} \overset{n}{\sum_{i}} R_{i}$ (1)

将 $\overset{̅}{R}$ 与R进行一元线性回归, 计算每条光谱数据的平移量Bias_i和漂移量Gain_i

$R_{i} = Gai n_{i} \overset{̅}{R} + Bia s_{i}$ (2)

则经过修正后的光谱数据为R_i,_MSC

$R_{i, MSC} = \frac{R_{i} - Bia s_{i}}{Gai n_{i}}$ (3)

1.3.2 微分变换

微分变换能够消除背景漂移的影响, 常用的微分变换有一阶微分(first-order differential, FD)和二阶微分(second-order differential, SD), 其中光谱一阶微分能够消除线性背景以及噪声光谱, 计算公式为

$R (λ_{i})_{FD} = \frac{R (λ_{i + 1}) - R (λ_{i})}{λ_{i + 1} - λ_{i}}$ (4)

式(4)中, λ _i为波长, R(λ _i)为在波长λ _i处的值。

光谱二阶微分能够提高光谱峰的分辨能力, 同时也能够减弱噪声的干扰, 计算公式如式(5)

$R (λ_{i})_{SD} = \frac{R (λ_{i + 2}) - 2 R (λ_{i + 1}) + R (λ_{i})}{(λ_{i + 1} - λ_{i})^{2}}$ (5)

1.3.3 倒数对数变换

光谱倒数对数变换(spectral reciprocal logarithmic, SRL)能够增强相似光谱之间的差别, 计算公式如式(6)

$R (λ_{i})_{SRL} = lo g_{10} (\frac{1}{R (λ_{i})})$ (6)

1.3.4 连续小波变换

连续小波变换(continuous wavelet transform, CWT)基于平移和缩放母小波函数, 可以增强光谱的细节信息。纸张样本的原始光谱反射率通过小波基函数, 在不同尺度下生成一系列小波系数。其计算公式为

$\begin{array}{l} W_{R (a, b)} = \int R (λ) Ψ_{a, b (λ)} d λ \\ Ψ_{a, b (λ)} = \frac{1}{\sqrt[]{a}} Ψ (\frac{λ - b}{a}) \end{array}$ (7)

式(7)中, R(λ )为纸张反射率, W_R₍_a_,_b₎为小波系数, Ψ _a_,_b₍_λ₎为尺度因子为a、伸缩因子为b的小波基函数。基于2ⁿ(n=1, 2, 3, …, 11)共选择了11个尺度进行连续小波变换, 小波基函数为gaus1, 对原始光谱、原始光谱一阶微分、多元散射校正、多元散射校正光谱一阶微分进行连续小波分解。

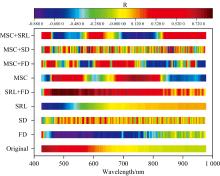
在本研究中, 共进行原始光谱一阶微分(FD)、原始光谱二阶微分(SD)、原始光谱倒数对数(SRL)、原始光谱倒数对数一阶微分(SRL-FD)、多元散射校正(MSC)、多元散射校正光谱一阶微分(MSC-FD)、多元散射校正光谱二阶微分(MSC-SD)、多元散射校正光谱倒数对数(MSC-SRL)和连续小波变换12种处理, 其中前11种方法处理后光谱曲线如图1所示。

	Figure Option View Download New Window
	图1 不同光谱变换下的光谱曲线图Fig.1 Spectra obtained by different spectral transformations

1.4 特征波长选择

竞争自适应重加权采样算法(competitive adaptative reweighted sampling, CARS)的核心是在建立偏最小二乘(partial least squares, PLS)模型的过程中, 通过蒙特卡洛采样的方式迭代, 剔除在PLS回归模型中回归系数绝对值权重较小的点。基于这一策略, CARS方法迭代地构建多个子集, 最终选择具有最小均方根误差的子集所包含的波段作为特征波长。

在本研究中, 采用CARS和相关系数的方法选择特征波长。

1.5 建模方法及精度评价

深度学习模型在回归预测中也取得了较好的成果, 因此, 基于支持向量机回归(support vector regression, SVR)、袋装(Bagging)集成算法和提升(Boosting)集成算法进行实验。

1.5.1 SVR算法

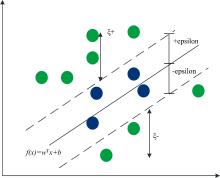
SVR算法旨在找到数据空间中的一个分离超平面, 使所有数据点尽可能接近分离超平面^[15], 示意图如图2所示。

	Figure Option View Download New Window
	图2 SVR示意图Fig.2 Diagram of SVR

SVR模型表达式可记为

$f (x) = w^{T} x + b$ (8)

式(8)中, w为法向量, b为位移项, 超平面由法向量和位移项确定。引入变量ζ ⁺和ζ ^-, SVR的目标函数则为

$\min_{(w, b, ζ^{+}, | ζ^{-})} - \frac{1}{2} ‖ w ‖^{2} + C \overset{m}{\sum_{i}} (ζ^{+} + ζ^{-})$ (9)

$\begin{array}{l} s.t. \{\begin{array}{l} y_{i} - f (x) \leq ε + ζ_{i}^{+} \\ f (x) - y_{i} \leq ε + ζ_{i}^{-} \\ ζ_{i}^{+}, ζ_{i}^{-} \geq 0, i = 1, 2, \dots, m \end{array} \end{array}$ (10)

其中损失函数为

$Γ (f (x) - y) = \{\begin{array}{l} |f (x) - y| - ε, & if |f (x) - y| \geq ε \\ 0, & else \end{array}$ (11)

采用RBF作为核函数, 采用网格法进行参数优化。

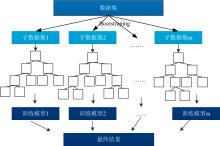
1.5.2 Bagging系列集成算法

Bagging系列算法是一种典型的集成算法^[16], 是一种有放回的随机抽样, 代表方法有随机森林(random forest, RF)。 Bagging系列算法的一般过程为: (1)将原始训练数据集基于Bootstraping方法抽取n个样本, 重复进行m次, 获得m个子样本集; (2)对每个子样本集进行训练, 获得m个训练模型; (3)对m个训练模型进行集成: 在分类时, 采用投票的方法, 将样本类别预测为投票最多的类别, 在回归时, 预测值为各个决策树的加权均值。在此基础上, 如果树的节点切分依据是随机选择k个特征, 并从这k个特征选择最优的特征, 并使用CART决策树作为学习器, 就称为随机森林模型, 训练过程如图3所示。

	Figure Option View Download New Window
	图3 RF结构示意图Fig.3 Diagram of RF

1.5.3 提升(Boosting)系列集成算法

Boosting系列算法是一种典型的集成算法, 由一系列具有依赖关系的弱学习器通过加权组成, Boosting系列算法基本思想是通过将训练样本赋权重, 训练弱学习器1, 然后基于误差率更新样本权重, 根据更新权重后的样本集训练弱学习器2, 直到获得了n个弱学习器, 将这n个弱学习器集成获取最终的一个强学习器。常用的算法有: 自适应提升算法(adaptive boosting, AdaBoost)、梯度提升决策树(gradient boosting decision tree, GBDT)、极端梯度提升(eXtreme gradient boosting, XGBoost)等^{[17, 18]}。

AdaBoost算法在初始化时, 将n个样本的权重都赋值为1/n, 然后通过不断的提高误差大的样本的权重, 降低误差小的样本的权重进行样本权重的更新, 每个弱学习器权重计算公式为

$α = \frac{1}{2} \ln \frac{1 - ε}{ε}$ (12)

式(12)中, α 表示弱学习器的权重, ε 表示错误率。由于AdaBoost算法关注错误率较大的样本, 因而要求数据比较均衡, 对异常样本非常敏感。

对110个数据集按照类别, 在每类中采用基于联合x-y距离的样本集划分方法(sample set partitioning based on joint x-y distance, SPXY)划分为7:3, 最终获取训练数据77组, 验证数据33组, 共选择了3种建模方法进行纸张粘度估算, 分别是SVR、 RF和AdaBoost。

1.5.4 精度评价

精度评价矩阵采用决定系数(coefficient of determination, R²)和均方根误差(root mean square error, RMSE), 计算如式(13)和式(14)

$R^{2} = \frac{\sum {(y' - \overset{̅}{y})}^{2}}{\sum {(y - \overset{̅}{y})}^{2}}$ (13)

$\begin{array}{l} RMSE = \sqrt[]{\frac{\sum {(y' - y)}^{2}}{n}} \end{array}$ (14)

式(13)和式(14)中, y和y'分别为粘度的真实值和反演值, $\overset{̅}{y}$ 为y平均值, n为样本的个数。

所有的高光谱数据处理和模型建立均以Python语言实现。

2 结果与讨论

2.1 特征波长选择

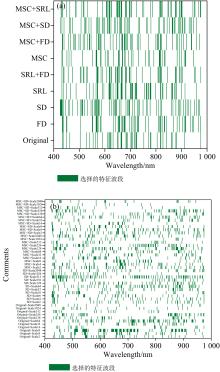
2.1.1 CARS算法特征波长选择

在CARS算法中, 将蒙特卡洛采样次数设置为100, 采用5折交叉验证, 运行10次后, 取最小均方根误差作为最终选择的特征变量, 如图4所示。在原始光谱中共选择了47个波段, 特征光谱主要分布在500~900 nm之间; 在SRL+FD光谱中, 共选择了57个波段, 主要分布在500~600及800~900 nm之间; 在原始光谱、 FD、 SD、 SRL、 SRL-FD、 MSC、 MSC-FD、 MSC-SD和MSC-SRL共9种类型中, CARS算法选择的最多的特征波段出现在MSC-SRL中, 共有65个波段。在连续小波变换中, 选择的特征波段基本上均匀分布在400~900 nm之间, 其中选择的特征波段最多和最小个数出现原始光谱分解尺度为8和MSC+SD, 分解尺度为1 024, 特征波段的个数分别是98和9。

	Figure Option View Download New Window
	图4 基于CARS-PLS选择的特征波段分布图 (a): 微分及多元散射校正等变换; (b): 连续小波变换Fig.4 Distributions of feature wavelength bands selected based on CARS-PLS (a): Differential and multi-element scattering corrections; (b): Continuous wavelet transform

2.1.2 相关系数法特征波长选择

根据相关系数法(correlation coefficient, R), 计算每个波段与粘度的相关系数, 如图5所示, 在原始光谱、 FD、 SD、 SRL、 SRL+FD、 MSC、 MSC+FD、 MSC+SD和MSC+SRL中, 与纸张粘度相关系数最高的波段分别为: 430、 481、 578、 430、 502、 740、 577、 858和740 nm处。同时, SRL+FD与纸张粘度的相关系数最大, 为0.873, 说明原始光谱经过倒数对数一阶微分变换后, 能够显著增加光谱中关于纸张粘度的信息。原始光谱经过二阶微分变换后, 最大相关系数为0.57, 小于原始光谱的最大相关系数0.75, 表明原始光谱经过二阶微分变换后, 减少了纸张粘度的光谱信息; 但是经过多元散射校正二阶微分变换后, 最大相关系数为0.78, 高于原始光谱信息, 说明多元散射校正能够有效的增加纸张粘度的光谱信息。最后, 在上述八种光谱变换中, 除了SD变换, 其他变换后的最大相关系数均大于原始光谱, 表明了光谱变换的有效性, 能够增大纸质粘度的光谱信息。

	Figure Option View Download New Window
	图5 纸张粘度与光谱特征相关系数分布图Fig.5 Distribution of correlation coefficients between paper viscosity and spectral features

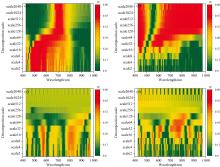
对原始光谱、 FD、 MSC和MSC+FD四种光谱经过连续小波变换的小波系数与纸张粘度的决定系数, 如图6所示。对于原始光谱, 随着分解尺度的增加, 光谱中包含的纸质粘度信息有所减少, 而对于原始光谱一阶微分, 则有所增加。对于四种光谱而言, 最大相关系数分别出现在分解尺度8, 484 nm, 分解尺度2 048, 976 nm, 分解尺度8, 575 nm和分解尺度32, 771 nm处, 分别为0.87、 0.89、 0.77和0.78。

Figure Option
View Download New Window

图6 纸张粘度与光谱特征决定系数分布图
(a): 原始光谱; (b): 原始光谱一阶微分; (c): 多元散射校正; (d): 多元散射校正一阶微分Fig.6 Distribution of determination coefficients between paper viscosity and spectral features
(a): Original Spectrum; (b): First order derivative of original spectrum; (c): Multiple scatter correction; (d): First order derivative of multiple scatter corrected spectrum

根据上述结果, 将相关系数满足0.001显著水平(|R|> =0.314)的波段作为特征波段, 结果如图7所示: 对于原始波段, 特征波段分布在425~560 nm之间, 对于SRL+FD, 特征波段主要分布在425~830以及886~887、 913~917 nm之间; 对于小波变换而言, 在MSC+Scale1024、 MSC+Scale2048、 MSC+SD+Scale256、 MSC+SD+Scale512和MSC+SD+Scale1024上, 几乎选择了所有波段, 说明在这些分解尺度上, 对纸张粘度的光谱信息也进行了分解。

	Figure Option View Download New Window
	图7 基于相关系数选择的特征波段分布图 (a): 微分及多元散射校正等变换; (b): 连续小波变换Fig.7 Distribution of feature wavelength bands selected based on correlation coefficients (a): Differential and multi-element scattering corrections; (b): Continuous wavelet transform

同时选择小波分解相关系数最高的前三个尺度作为最优分解尺度, 作为后续建模输入。对于原始光谱, 最优分解尺度为2、 4和8; 对于原始光谱一阶微分, 最优分解尺度为512、 1 024和2 048; 对于MSC, 最优分解尺度为2、 4和8; 对于MSC+FD, 最优分解尺度为2、 8和32。

2.2 反演模型精度对比

根据CARS和R选择的特征波段作为输入, 建立SVR、 RF和AdaBoost反演模型, 结果如表1和表2所示。结果表明, 在基于CARS算法选择的特征波长和预处理算法组合中, 原始光谱倒数对数一阶微分作为输入, 模型验证精度最高, SVR、 RF和AdaBoost模型的R²分别为0.96、 0.93和0.93, RMSE为14.80、 18.33和19.79 mL· g^-1; 其中, 原始光谱分解尺度为2的连续小波分解作为输入, AdaBoost模型的精度与原始光谱倒数对数一阶微分作为输入的精度基本一致, R²均为0.93。同时, 在基于相关系数法选择的特征波长和算法组合中, 也表现出相同的特性, 即原始光谱倒数对数一阶微分作为输入, 模型验证精度最高, SVR、 RF和AdaBoost模型的R²分别为0.96、 0.93和0.93, RMSE分别为13.47、 19.23和17.93 mL· g^-1。基于CARS算法选择的特征波段个数小于基于R方法选择的个数, 但其最高精度模型均为SVR模型和原始光谱倒数对数一阶微分输入, R²均为0.96, RMSE相差无几, 说明基于CARS特征选择算法的有效性。以上结果表明, 在基于高光谱对纸张粘度估算时, 原始光谱倒数对数一阶微分和SVR模型精度表现最优。

表1 基于CARS选择特征的不同模型精度评价 Table 1 Performances of different models based on CARS feature selection

光谱数据+SVR	训练数据集		光谱数据+RF	训练数据集		光谱数据+AdaBoost	训练数据集
光谱数据+SVR	R²	RMSE	光谱数据+RF	R²	RMSE	光谱数据+AdaBoost	R²	RMSE
原始波段	0.92	22.81	原始波段	0.95	20.20	原始波段	0.91	26.89
FD	0.93	22.88	FD	0.96	18.22	FD	0.96	15.38
SD	0.83	34.76	SD	0.96	18.22	SD	0.97	15.11
SRL	0.92	23.23	SRL	0.91	24.98	SRL	0.88	28.97
SRL+FD	0.96	17.57	SRL+FD	0.98	13.31	SRL+FD	0.97	13.83
MSC	0.96	15.98	MSC	0.93	22.79	MSC	0.94	20.27
MSC+FD	0.94	20.27	MSC+FD	0.97	14.58	MSC+FD	0.95	19.69
MSC+SD	0.98	12.41	MSC+SD	0.97	15.81	MSC+SD	0.97	15.82
MSC+SRL	0.98	8.62	MSC+SRL	0.94	21.39	MSC+SRL	0.95	18.34
Ori2	0.97	14.51	Ori2	0.97	13.99	Ori2	0.96	17.59
Ori4	0.94	20.06	Ori4	0.96	17.32	Ori4	0.94	20.37
Ori8	0.94	21.05	Ori8	0.97	14.13	Ori8	0.95	18.78
FD512	0.87	29.98	FD512	0.91	25.20	FD512	0.94	20.62
FD1024	0.86	31.27	FD1024	0.97	14.88	FD1024	0.94	19.82
FD2048	0.90	25.69	FD2048	0.96	17.34	FD2048	0.96	17.64
MSC2	0.99	2.79	MSC2	0.97	15.85	MSC2	0.95	19.73
MSC4	0.90	26.23	MSC4	0.96	16.08	MSC4	0.94	20.59
MSC8	0.90	27.07	MSC8	0.97	15.64	MSC8	0.94	21.10
MSC+FD2	0.98	12.88	MSC+FD2	0.97	16.76	MSC+FD2	0.97	14.75
MSC+FD8	0.98	12.33	MSC+FD8	0.97	16.56	MSC+FD8	0.96	17.80
MSC+FD32	0.98	10.19	MSC+FD32	0.87	31.04	MSC+FD32	0.84	33.26
光谱数据+SVR	测试数据集		光谱数据+RF	测试数据集		光谱数据+AdaBoost	测试数据集
光谱数据+SVR	R²	RMSE	光谱数据+RF	R²	RMSE	光谱数据+AdaBoost	R²	RMSE
原始波段	0.94	17.32	原始波段	0.88	24.11	原始波段	0.87	25.52
FD	0.93	20.07	FD	0.87	25.21	FD	0.86	27.27
SD	0.85	29.43	SD	0.88	25.21	SD	0.85	27.21
SRL	0.94	17.83	SRL	0.91	21.61	SRL	0.88	24.76
SRL+FD	0.96	14.80	SRL+FD	0.93	18.33	SRL+FD	0.93	19.79
MSC	0.89	26.03	MSC	0.86	28.69	MSC	0.84	29.22
MSC+FD	0.93	19.08	MSC+FD	0.86	25.74	MSC+FD	0.89	23.26
MSC+SD	0.82	30.04	MSC+SD	0.86	26.94	MSC+SD	0.88	24.81
MSC+SRL	0.91	22.21	MSC+SRL	0.85	29.36	MSC+SRL	0.83	29.90
Ori2	0.96	15.55	Ori2	0.90	22.23	Ori2	0.93	19.32
Ori4	0.94	17.31	Ori4	0.84	28.64	Ori4	0.81	32.24
Ori8	0.94	17.76	Ori8	0.89	22.92	Ori8	0.90	22.91
FD512	0.87	25.42	FD512	0.84	27.84	FD512	0.85	27.13
FD1024	0.91	21.40	FD1024	0.88	23.76	FD1024	0.86	25.89
FD2048	0.90	21.98	FD2048	0.88	24.29	FD2048	0.87	25.68
MSC2	0.91	21.90	MSC2	0.86	25.98	MSC2	0.90	23.07
MSC4	0.84	27.84	MSC4	0.88	24.42	MSC4	0.88	24.02
MSC8	0.87	25.95	MSC8	0.86	26.30	MSC8	0.87	25.42
MSC+FD2	0.84	28.87	MSC+FD2	0.85	27.49	MSC+FD2	0.84	28.39
MSC+FD8	0.87	28.14	MSC+FD8	0.78	33.53	MSC+FD8	0.90	22.58
MSC+FD32	0.86	27.48	MSC+FD32	0.67	41.87	MSC+FD32	0.70	38.25

注: RMSE单位为mL· g^-1

Note: The unit of RMSE is mL· g^-1 (The same below)

表1 基于CARS选择特征的不同模型精度评价 Table 1 Performances of different models based on CARS feature selection

表2 基于R选择特征的不同模型精度评价 Table 2 Performances of different models based on R feature selection

光谱数据+SVR	训练数据集		光谱数据+RF	训练数据集		光谱数据+AdaBoost	训练数据集
光谱数据+SVR	R²	RMSE	光谱数据+RF	R²	RMSE	光谱数据+AdaBoost	R²	RMSE
原始波段	0.92	23.64	原始波段	0.94	20.77	原始波段	0.92	26.20
FD	0.97	15.92	FD	0.96	16.15	FD	0.96	16.40
SD	0.96	16.22	SD	0.93	24.81	SD	0.96	20.85
SRL	0.92	23.28	SRL	0.95	19.38	SRL	0.91	26.51
SRL+FD	0.97	15.84	SRL+FD	0.98	12.43	SRL+FD	0.96	15.73
MSC	0.98	10.43	MSC	0.97	16.43	MSC	0.95	19.12
MSC+FD	0.99	3.76	MSC+FD	0.96	16.54	MSC+FD	0.96	16.31
MSC+SD	0.98	13.07	MSC+SD	0.96	17.90	MSC+SD	0.98	12.66
MSC+SRL	0.98	10.44	MSC+SRL	0.96	17.12	MSC+SRL	0.96	17.11
Ori2	0.93	21.93	Ori2	0.97	13.70	Ori2	0.97	14.20
Ori4	0.97	15.36	Ori4	0.97	13.72	Ori4	0.96	17.27
Ori8	0.95	18.71	Ori8	0.97	14.73	Ori8	0.96	15.96
FD512	0.94	20.51	FD512	0.94	20.43	FD512	0.95	19.05
FD1024	0.88	28.77	FD1024	0.92	23.53	FD1024	0.97	15.80
FD2048	0.96	17.18	FD2048	0.94	19.60	FD2048	0.96	16.22
MSC2	0.97	15.59	MSC2	0.96	18.06	MSC2	0.88	29.11
MSC4	0.98	10.08	MSC4	0.97	16.06	MSC4	0.97	15.63
MSC8	0.96	17.45	MSC8	0.97	15.90	MSC8	0.96	16.94
MSC+FD2	0.97	16.00	MSC+FD2	0.97	15.71	MSC+FD2	0.97	13.82
MSC+FD8	0.97	14.14	MSC+FD8	0.97	15.66	MSC+FD8	0.96	16.20
MSC+FD32	0.93	23.83	MSC+FD32	0.96	16.34	MSC+FD32	0.94	20.35
光谱数据+SVR	测试数据集		光谱数据+RF	测试数据集		光谱数据+AdaBoost	测试数据集
光谱数据+SVR	R²	RMSE	光谱数据+RF	R²	RMSE	光谱数据+AdaBoost	R²	RMSE
原始波段	0.92	20.36	原始波段	0.89	23.71	原始波段	0.91	22.46
FD	0.96	13.64	FD	0.92	20.68	FD	0.95	17.25
SD	0.79	37.86	SD	0.82	36.40	SD	0.83	34.43
SRL	0.93	19.13	SRL	0.87	24.96	SRL	0.90	22.87
SRL+FD	0.96	13.47	SRL+FD	0.93	19.23	SRL+FD	0.93	17.93
MSC	0.92	21.08	MSC	0.78	34.05	MSC	0.84	29.42
MSC+FD	0.91	21.85	MSC+FD	0.80	31.23	MSC+FD	0.85	26.70
MSC+SD	0.91	22.83	MSC+SD	0.87	25.57	MSC+SD	0.85	27.25
MSC+SRL	0.92	21.07	MSC+SRL	0.81	32.10	MSC+SRL	0.82	30.20
Ori2	0.93	19.11	Ori2	0.89	22.81	Ori2	0.87	26.11
Ori4	0.94	17.86	Ori4	0.88	24.56	Ori4	0.90	22.78
Ori8	0.95	16.72	Ori8	0.90	22.87	Ori8	0.92	20.55
FD512	0.83	29.09	FD512	0.86	26.38	FD512	0.87	25.48
FD1024	0.86	26.12	FD1024	0.89	22.93	FD1024	0.87	25.23
FD2048	0.85	27.70	FD2048	0.90	22.46	FD2048	0.89	24.48
MSC2	0.89	23.20	MSC2	0.83	28.65	MSC2	0.87	25.22
MSC4	0.90	23.91	MSC4	0.90	22.73	MSC4	0.90	23.07
MSC8	0.87	26.06	MSC8	0.82	30.13	MSC8	0.84	27.88
MSC+FD2	0.85	27.33	MSC+FD2	0.89	23.33	MSC+FD2	0.89	23.33
MSC+FD8	0.89	23.28	MSC+FD8	0.86	25.98	MSC+FD8	0.86	26.22
MSC+FD32	0.81	31.10	MSC+FD32	0.71	39.84	MSC+FD32	0.74	37.31

表2 基于R选择特征的不同模型精度评价 Table 2 Performances of different models based on R feature selection

3 结论

针对纸张粘度估算, 基于已知老化程度的老化纸张高光谱信息数据库, 对比分析了不同的高光谱数据处理算法和特征光谱选择算法, 构建并筛选了能有效表征纸张粘度含量变化的最优反演模型, 为纸张粘度的无损分析提供了新的测定手段。研究结果表明: (1)SRL+FD数据处理能够显著增加光谱中关于纸张粘度的信息, 与纸张粘度的相关系数为0.873(502 nm), 而在原始光谱中, 430 nm处与粘度相关性最高, R为0.75; (2)对于原始光谱, 随着分解尺度的增加, 光谱中包含的纸质粘度信息有所减少, 且最大相关系数出现在分解尺度2的484 nm处; (3)在不同组合输入中, SRL+FD作为输入CARS的SVR模型精度最优, 在训练数据集和验证数据集中, R²分别为0.96和0.96, RMSE分别为17.57和14.80 mL· g^-1。表明高光谱技术在纸张粘度无损分析的适用性, 为纸张文物的保护和修复提供新思路。

参考文献

文献列表

[1]	WANG Hao(王昊). China Paper Newsletters(造纸信息), 2023, (6): 124. [本文引用:1]
[2]	LI Bin(李彬). Culture Industry(文化产业), 2023, (24): 76. [本文引用:1]
[3]	TONG Qing-xi, ZHANG Bing, ZHANG Li-fu(童庆禧, 张兵, 张立福). National Remote Sensing Bulletin(遥感学报), 2016, 20(5): 689. [本文引用:1]
[4]	ZHANG Li-fu, WANG Sa, ZHANG Yan, et al(张立福, 王飒, 张燕, 等). Acta Geodaetica et Cartographica Sinica(测绘学报), 2023, 52(7): 1126. [本文引用:1]
[5]	Balas C, Papadakis V, Papadakis N, et al. Journal of Cultural Heritage, 2003, 4(S1): 330. [本文引用:1]
[6]	Sun M, Zhang D, Wang Z, et al. Scientific Reports, 2015, 5: 14371. [本文引用:1]
[7]	WANG Le-le, LI Zhi-min, MA Qing-lin, et al(王乐乐, 李志敏, 马清林, 等). Dunhuang Research(敦煌研究), 2015, (3): 128. [本文引用:1]
[8]	Vermeulen M, Mirand a A S O, Tamburini D, et al. Heritage Science, 2022, 10(1): 44. [本文引用:1]
[9]	WU Wang-ting, ZHANG Chen-feng, GAO Ai-dong, et al(武望婷, 张陈锋, 高爱东, 等). Sciences of Conservation and Archaeology(文物保护与考古科学), 2017, 29(4): 45. [本文引用:1]
[10]	GUO Xin-lei, ZHANG Li-fu, WU Tai-xia, et al(郭新蕾, 张立福, 吴太夏, 等). Journal of Image and Graphics(中国图象图形学报), 2017, 22(10): 1428. [本文引用:1]
[11]	ZHOU Xin-guang, SHEN Hua, WU Lai-ming (周新光, 沈骅, 吴来明). Sciences of Conservation and Archaeology(文物保护与考古科学), 2020, 32(1): 56. [本文引用:1]
[12]	YI Xiao-hui, LONG Kun, REN Shan-shan, et al(易晓辉, 龙堃, 任珊珊, 等). Sciences of Conservation and Archaeology(文物保护与考古科学), 2018, 30(3): 21. [本文引用:1]
[13]	GAO Yu, SUN Xue-jian, LI Guang-hua, et al(高宇, 孙雪剑, 李光华, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2023, 43(9): 2960. [本文引用:2]
[14]	LI Yang(李扬). Paper Science and Technology(造纸科学与技术), 2021, 40(2): 46. [本文引用:1]
[15]	Guo Guodong, Fu Yun, Dyer Charles R, et al. IEEE Transactions on Image Processing, 2008, 17(7): 1178. [本文引用:1]
[16]	Breiman L. Machine Learning, 1996, 24: 123. [本文引用:1]
[17]	Chen T, Guestrin C. XGBoot: A Scalable Tree Boosting System, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016: 785. [本文引用:1]
[18]	Prokhorenkova L, Gusev G, Vorobev A, et al. CatBoost: Unbiased Boosting With Categorical Features, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2017: 6639. [本文引用:1]

2023

0.0

... 引言纸质文物承载着我国历史文化的传承和民族精神的延续^[1], 具有重要的政治、经济、文化和科学价值 ...

2023

0.0

... 随着时间和环境的改变, 如环境的温度、湿度、霉变、光照和紫外等, 纸张会出现老化现象, 严重影响文物的寿命和艺术价值^[2], 因此研究纸张的性能十分必要 ...

2016

0.0

... 高光谱遥感技术起源于20世纪80年代初期^[3], 通过获取目标物体在可见光谱到近红外范围内的连续光谱信息来反映目标物的特性, 具有光谱分辨率高、图谱合一的独特优势, 经过近40年的飞速发展, 已广泛应用于农业、环境、食品和考古等领域^[4] ...

2023

0.0

2003

0.0