在当前天文观测领域, 随着科学技术的不断进步, 高精度光谱仪成为了研究宇宙起源和演化的重要工具之一。 光纤阵列太阳光学望远镜(Fiber Arrayed Solar Optical Telescope, FASOT)利用光纤积分视场单元技术, 成功获取了多条磁敏谱线斯托克斯光谱数据^[1]。 FASOT系统利用光纤技术将望远镜观测到的天体光谱信息传输至光谱仪进行分析, 实现了高效、 精确的数据采集。 光纤作为光信号的传输媒介, 于1977年被Angel等人首次应用在天文望远镜中, 具有低损耗、 高稳定性等优点。 在天文中广泛应用, 例如单目标探测^[2]、 积分视场单元(IFU)^[3]以及多目标望远镜^[4]等。

通常采用成像光谱仪探测光纤光谱, 其原理是将位于光谱仪狭缝的光纤端面的光场通过色散元件后成像在探测器上。 在单模光纤中, 光纤内仅传输一个模式, 光纤出射端面的光场能量呈类高斯状分布。 在多模光纤中, 光纤内传输的模式数量与光纤芯径、 光纤数值孔径、 以及光源频率等因素相关。 不同模式的光信号传播途径不同, 位相延迟也不一样, 相互之间会发生干涉。 当光源为激光等相干光信号时, 光纤出射端面会形成高对比度的散斑图样。 当光源为白光等频带较宽的信号时, 由于各种频率的光形成的散斑相互叠加, 整体光斑看不到明显的散斑特性。 但是, 在中高光谱分辨率的光谱探测中, 例如视向速度测量^[5]、 太阳磁场测量^[6]等, 色散分辨率R常大于1 05^[7], 关注的光谱带宽通常只有几个纳米, 每个像素内对应的带宽仅为0.01 nm量级。 在这样窄的波段内, 会出现明显能量分布不均匀的现象。 在高光谱分辨率、 高信噪比的光谱测量中产生光纤模式噪声, 降低光谱测量精度。

近年来, 为了克服光纤模式噪声对光谱数据的干扰, 研究人员提出了多种扰模方式。 2018年Petersburg提出了一种通过搅动光纤来减轻模式噪声的方法。 通过在光纤中施加机械振动, 可以打破光纤中的模式耦合, 有效地减轻了模式噪声, 在视向速度的测量过程中模式噪声的影响被减少到3.2 cm· s^-1以下^[8]。 2019年Raskin利用旋转双扰频器, 大大减少模态噪声。 使视向速度测量精度从1.4 m· s^-1降低至5 cm· s-1^[7]。 2022年王嘉琦提出了一种基于变形镜抑制光纤模态噪声的技术方法, 通过动态改变变形镜的面型, 在单次曝光时间内平滑光纤引起的散斑花样, 提高定标光谱的质心稳定性。 针对分辨率R=100 000的光谱仪, 单根定标谱线引起的视向速度定标误差约为19.8 cm· s^-1, 可以达到国际上主要光谱仪的定标精度^[9]。

为了取得更好的扰模效果, 本工作设计了一种多维机械扰模结构, 并提出了一种以能量中心位置标准偏差作为光纤模式散斑能量离散度以及对天文光纤光谱测量精度影响的评价函数, 可以定量分析散斑对光谱测量精度的影响。

在光纤中, 光波以导波模式传播。 多模中支持的模式数量由归一化频率V决定

V=2πaλncore2-ncladding2(1)

式(1)中, a为光纤纤芯直径, λ 为入射光波长, n_core为纤芯折射率, n_cladding为包层折射率。 光纤支持的模式数量在V> 10时可以近似为V²/2。

每一种导波模式都对应于特定的光场分布, 且不同模式的光波相对于光纤的轴线以不同角度传播, 因此它们在光纤中传播的路径存在差异, 导致它们从光纤一端到达另一端的相位延迟不同^[10]。 对于单色输入光, 光纤出射端面上任意一点的光场可以写为各导波模式复振幅贡献的总和^[11]

E(r, θ, λ, L)=∑mAmΨm(r, θ, λ)exp[-iβm(λ)L](2)

式(2)中, A_m为第m个模式的振幅, Ψ _m为第m个模式的空间轮廓, β _m为传播系数, λ 为入射光真空中波长, L为传播路径的长度。

给定模式的相位差为

Δφ=2πλΔnL(3)

式(3)中, Δ φ 是相位差, Δ n是不同模式之间的折射率差。 在长距离传播后, 不同模式的累积相位延迟相差2π 以上, 因此当不同模式的光线在光纤端面叠加时会形成散斑。

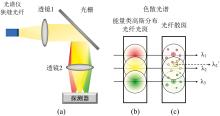
传统光谱仪采用光栅进行色散, 其将狭缝处光纤端面不同波长下的散斑图样投射到成像器件的不同位置, 如图1(a)所示。 当光纤为单模光纤时, 光纤出射光斑的能量分布为类高斯分布, 红色, 黄色和绿色光斑的能量中心位置分别代表λ ₁, λ ₂和λ ₃三个波长的空间位置, 如图1(b)所示。 当光纤为多模光纤时, 光纤出射光斑对应不同波长均呈现为颗粒状的散斑, 如图1(c)所示。 可以看出不同波长的散斑图样并不相同, 造成各波长能量中心并不一致, 并偏离光纤的几何中心。 在光谱测量中, 尤其是高光谱分辨率的情况, 能量中心的不稳定将造成光谱测量精度的下降。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 成像光谱仪原理Fig.1 Principle of imaging spectrometer

当光纤静止时, 由于光线传播路径不变, 形成的散斑图样是稳定的; 当改变光纤状态时, 光纤内各模式的相位延迟发生改变, 散斑图样也随之变化。 因此可以利用将光纤放置于振动平台上, 通过抖动光纤改变光纤中不同模式的传输相位, 改变出射端的散斑图样, 从而实现散斑均匀化。 当只采用一个运动方向固定的机械振动源来改变光纤的形态时, 光纤的运动路径是固定的, 产生的光纤散斑具有规律性, 不能很好地将散斑图样平均掉。 当光纤的运动路径无规律时, 光纤散斑的形貌会无规则改变, 均匀化效果最好, 散斑的影响可以降到最小。 为了使光纤运动路径接近随机化, 提出多维机械扰模方法, 即在不同方向、 光纤不同位置上对光纤实施不同频率的振动干扰, 使各个模式的相位改变更加随机, 实现更好的散斑抑制效果。

为了比较不同机械扰模方法的效果, 选用了激光作为光源, 分析激光经过多模光纤后出射光斑的散斑分布以及机械扰模对散斑的抑制效果。 实验装置如图2所示。 光源为一个能量可调的650 nm波长半导体激光器, 激光器出射光束首先被耦合至工作波段为500~750 nm的单模光纤中, 单模光纤与测试多模光纤通过熔接机进行对准。 测试多模光纤的长度为5 m, 芯径为35 μ m, 包层直径为110 μ m, 涂敷层直径为125 μ m, 数值孔径为0.12, 自然地缠绕在多维机械扰动装置上。 多维机械扰动装置由三个不同方向、 不同频率的往复运动的机械结构组成。 通过调节三个机械装置以不同的频率做往复运动, 使光纤产生尽可能多的不同的弯曲状态(宏弯曲), 以接近随机的扰模效果。 为了避免光纤缠绕, 扰动装置预留孔位足够大, 且整个光纤在测试过程中无拉力。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 多维度机械扰模系统实验示意图Fig.2 Diagram of the multi-dimensional mechanical disturbance system

光纤另一端由光纤夹持器固定, 并用放大倍率为40倍、 数值孔径为0.4的物镜对光纤端面放大成像。 采用分辨率为5 496× 3 672、 像元大小为2.4 μ m的CCD拍摄光纤端面散斑图样。 单模光纤出射激光功率为3 mW, CCD曝光时间为1 s。

首先将长度为5 m、 芯径为35 μ m的光纤在自由状态下静置, 释放应力, 连续拍摄1 000张散斑图并进行叠加平均[如图3(a)]。 可以看出, 由于没有扰动, 散斑图样不发生变化。 然后用手微扰光纤, 1 000张散斑图叠加平均后得到较为均匀的强度分布[如图3(b)]。 再分别采用一维和多维机械扰模装置扰动光纤, 分别拍摄1 000张光纤端面散斑图, 并进行叠加平均, 得到了不同的扰模效果[如图3(c, d)]。 单从叠加平均图效果看, 手动扰模效果最好, 其次是多维扰动效果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同扰动模式下1 000张散斑图叠加平均的效果 (a): 无扰动; (b): 手动扰动; (c): 一维扰动; (d): 多维扰动Fig.3 The average effect of 1 000 speckle patterns under different kinds of disturbance (a): Without disturbance; (b): Manual disturbance; (c): One-dimensional disturbance; (d): Multi-dimensional disturbance

在分析光纤天文光谱图像时, 需要将一根光纤的光谱数据沿垂直色散的方向进行求和, 得到光纤光谱对色散方向的投影数据, 得到对应不同波长的测量光谱。 如果光纤散斑造成光纤出射端能量中心偏离光纤中心, 则其在色散方向的投影就会偏离真实的光谱分布。 为了定量分析这种散斑对光谱测量结果的影响, 测量了激光信号经过光纤后的散斑能量中心偏离光纤几何中心的情况。

如图4所示, 首先对光纤端面散斑的轮廓进行圆形拟合, 提取散斑边界(绿圈), 计算散斑的几何中心位置(绿点)及散斑半径; 然后以散斑图像各像素强度为权重, 计算散斑能量中心(红点)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
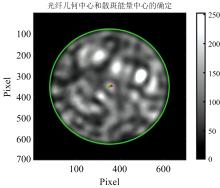	图4 光纤散斑几何中心和散斑能量中心的确定Fig.4 Determination of the geometric center and energy center of the optical fiber speckle

散斑能量中心(X, Y)的计算公式为

(X, Y)=∑j∑i(Ii, jxi, j, Ii, jyi, j)∑j∑iIi, j(4)

式(4)中, i和j分别为像素所在的行和列; I_{i, j}为第i行、 第j列像素的光强度, 作为加权平均的权重; (x_{i, j}, y_{i, j})为第i行、 第j列像素的坐标。

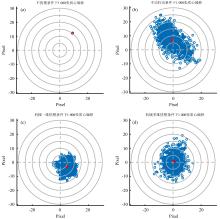
为了比较不同扰动方式下散斑抑制效果, 我们计算了如图3所示的四种情况下1 000散斑能量中心与几何中心偏移距离的分布情况, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同扰动模式下1 000张散斑图能量中心偏移分布 (a): 无扰动; (b): 手动扰动; (c): 一维扰动; (d): 多维扰动Fig.5 Offset distribution of energy centers of 1 000 speckle patterns under different kinds of disturbance (a): Without disturbance; (b): Manual disturbance; (c): One-dimensional disturbance; (d): Multi-dimensional disturbance

从图5中可以看出, 手动扰模条件下散斑能量中心分布范围最大, 意味着散斑去除效果最好, 但能量中心的分布并不均匀, 具有一定程度的分散, 造成平均能量中心[图5(b)中红点]偏离光纤几何中心。 多维扰模下能量中心分布最均匀, 能量中心偏离光纤几何中心也最少。 具体的偏离的像素值和相对偏离如表1所示, 可以看到机械多维扰模可以得到最佳的偏移量, 光谱测量精度最高。

表1

Table 1

表1(Table 1)

表1 不同扰模条件下1 000张散斑质心偏移情况 Table 1 Centroid shifts of 1 000 speckles under different kinds of disturbance 平均质心偏移 坐标(像素) 平均质心偏移 距离(像素) 相对偏移 /% 手动抖动 (-0.46, 6.82) 6.84 1.2 机械一维扰模 (4.59, -3.19) 5.59 1.0 机械多维扰模 (0.55, 0.43) 0.70 0.1

表1 不同扰模条件下1 000张散斑质心偏移情况 Table 1 Centroid shifts of 1 000 speckles under different kinds of disturbance

为了探究该种光纤在多维机械扰模条件下合适的曝光时间, 采用多张图片累加的方式模拟曝光时间的延长。 在1张散斑、 10张散斑叠加、 100张散斑叠加和500张散斑叠加的条件下, 给出每种条件下散斑图的能量分布, 如图6所示, 并在每种条件下随机选择了50张散斑图的能量中心分布结果, 如图7所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同张数散斑叠加结果Fig.6 Results of speckle superposition with different numbers

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同张数散斑叠加下50个散斑能量中心偏移的分布Fig.7 Offset distribution of 50 speckle energy centers under the superposition of speckle with different numbers

在图6中, 随着叠加的散斑数量增加, 散斑能量的分布逐渐均匀化, 散斑对比度下降。 在图7中, 随着叠加的散斑数量增加, 能量中心与光纤几何中心的偏移距离逐渐稳定。 因此, 当这种散斑图样向色散方向投影后, 散斑能量中心更加接近理想的光波长, 光谱测量精度越高。

为了对比分析不同散斑叠加数量下能量中心的离散度和光谱测量精度, 可以采用散斑能量中心位置分布的标准偏差σ , 如式(5)所示

σ=∑k=1N[(xk-X)2+(yk-Y)2]N(5)

式(5)中, N为参与叠加的散斑数量, (x_k, y_k)为每一个散斑能量中心坐标, (X, Y)为N个散斑中心的平均位置。

通过计算, 图7中四种条件下50个能量中心位置标准偏差σ 分别为5.02、 1.76、 0.38以及0.36个像素。 可见, 100张叠加和500张叠加的能量中心标准偏差相差不大, 只需要叠加100张(对应单张散斑图曝光时间的100倍)即可得到较为理想的扰模效果。 此时的标准偏差仅为单张散斑图的1/13。

为了探究该种光纤在多维机械扰模条件下合适的扰动频率, 我们在不同的扰模频率下对1 000张散斑的平均质心偏移进行了测试, 测试结果如表2和表3所示。 受到驱动电机转速的限制, 本研究中, 往复运动机械装置带动光纤可产生的频率范围为0.3~1.7 Hz, 振幅设置为6 cm。 分别在三个扰模装置运动频率相同和不同的条件下开展测试。

表2

Table 2

表2(Table 2)

表2 同频条件下1 000张散斑的质心偏移情况 Table 2 Centroid shifts of 1 000 speckles under the same disturbed frequency 扰模频率 /Hz 平均质心偏移 坐标(像素) 平均质心偏移 距离(像素) 相对偏移 /% 0.4-0.4-0.4 (-2.89, 2.47) 3.80 0.66 0.8-0.8-0.8 (0.08, -0.46) 0.47 0.08 1.2-1.2-1.2 (0.02, 0.21) 0.21 0.04 1.6-1.6-1.6 (0.39, -0.06) 0.39 0.07

表2 同频条件下1 000张散斑的质心偏移情况 Table 2 Centroid shifts of 1 000 speckles under the same disturbed frequency

表3

Table 3

表3(Table 3)

表3 不同频条件下1 000张散斑的质心偏移情况 Table 3 Centroid shifts of 1 000 speckles under different disturbed frequencies 扰模频率 /Hz 平均质心偏移 坐标(像素) 平均质心偏移 距离(像素) 相对偏移 /% 0.3-0.5-0.7 (-0.40, -0.55) 0.68 0.12 0.8-1.0-1.2 (-0.52, -0.16) 0.54 0.09 1.3-1.5-1.7 (-0.31, -0.23) 0.39 0.07

表3 不同频条件下1 000张散斑的质心偏移情况 Table 3 Centroid shifts of 1 000 speckles under different disturbed frequencies

表2展示了在三个扰模装置的频率相同时的测试结果。 当扰模频率为0.4-0.4-0.4 Hz时, 平均质心偏移距离为3.80个像素, 要远大于其他三组扰模频率, 这是由于扰模频率过低。 扰模频率应大于曝光时间的倒数^[12], 过低的扰模频率使得相同曝光时间内散斑图案变化少, 不易使散斑均匀。 在本实验中, 曝光时间为1 s。 因此实验中, 随着扰模频率的逐渐增加, 平均质心偏移距离呈现下降趋势, 在频率大于1 Hz时均获得了较好的散斑抑制效果。

之后, 三个扰模装置被设置为不同频率, 实验结果列举在表3中。 结合表2和表3可以看出, 三个扰模装置的频率相同与否对扰模效果并没有明显的影响。 与频率相同时相似, 随着扰模器频率的升高, 散斑平均质心偏移距离逐渐减小。 但是值得注意的是, 随着扰动频率的增大, 光纤受到的应力也随之增加, 光纤更容易损坏, 因此扰模器的频率不宜过高。

为了探究多维机械扰模装置的振幅对散斑质心的影响, 我们在不同振幅下对1 000张散斑的平均质心偏移进行了测试, 三个扰模装置振幅相同, 可选为4、 5或6 cm, 频率固定为1.2 Hz, 测试结果如表4所示。

表4

Table 4

表4(Table 4)

表4 不同振幅条件下1 000张散斑的质心偏移情况 Table 4 Centroid shifts of 1 000 speckles under different amplitudes 扰模振幅 /cm 平均质心偏移 坐标(像素) 平均质心偏移 距离(像素) 相对偏移 /% 4 (0.39, -0.34) 0.52 0.09 5 (0.28, -0.17) 0.33 0.06 6 (-0.08, -0.29) 0.30 0.05

表4 不同振幅条件下1 000张散斑的质心偏移情况 Table 4 Centroid shifts of 1 000 speckles under different amplitudes

从表4中可以看出, 随着振幅的增加, 平均质心偏移距离逐渐减小, 平均质心偏移距离从0.52个像素减小至0.3个像素, 最小相对偏移为0.05%。 这是由于随着振幅的增加, 散斑会获得更多的图案。 因此, 在机械结构条件允许的情况下, 振幅可以适当增大。 但是振幅和频率的选择需要有所权衡, 两者都较大时容易使光纤损坏。

在高色散光谱成像过程中, 由于每个像素对应的光谱带宽非常窄, 光纤出射端的像具有很好的相干性, 光谱图像会出现散斑, 光斑的能量中心会偏离光纤几何中心, 从而影响光谱测量精度。 为了抑制这种散斑, 我们采用散斑能量中心计算公式, 确定了光纤几何中心和散斑能量中心, 并采用能量中心的相对偏移的标准偏差来定量分析散斑的影响。 实验结果表明, 多维机械扰模抑制散斑效果优于不扰模、 手动扰模和一维机械扰模。 在多维机械扰模下, 叠加100张散斑图后, 标准偏差仅为单张散斑图的1/13。 当扰模器工作在较高的频率和振幅时, 散斑抑制效果更好。 对于本次实验中光纤而言, 频率选为1.2 Hz、 振幅选为6 cm最为合适。 在1 000次独立实验中, 散斑的平均质心偏移为0.21个像素, 相对偏移为0.04%。 选择的频率与振幅不宜过大以免使光纤损坏。 实际应用时, FASOT光纤由光缆保护, 每350根光纤被包裹在一根光缆内。 因此, 未来的工作将着眼于如何通过三维扰模系统实现对受光缆保护的多根天文光纤的散斑同时抑制。