激光诱导击穿光谱(LIBS)技术, 作为近年来备受瞩目的元素分析方法, 即将短脉冲激光聚焦于样品表面, 以实现样品材料表面击穿和等离子体生成。 通过捕获等离子体的辐射光谱, 基于一定的光谱数据处理模型, 反演待测样品中元素的含量^[1]。 相对于其他常见的元素分析技术, 如电感耦合等离子质谱(ICP-MS)^[2]、 拉曼光谱^[3]、 近红外光谱(NIR)^[4]、 X射线荧光光谱法(XRF)^[5]和原子吸收光谱法(AAS) ^[6]等, LIBS分析技术具有样品消耗量少、 原位、 高速、 多元素同时分析等多重优势。 目前, LIBS技术已广泛应用于食品^[7]、 工业^[8]、 材料科学^[9]、 冶金^[10]和环境科学^[11]等多个领域。 在日常生活和工业中, 不锈钢作为一种重要的基础材料, 有着广泛的应用, 不锈钢中的微量元素的类型和含量对其化学物理性质有着重要影响, 在包含镍(Ni)、 钛(Ti)和铬(Cr)三种元素的不锈钢中, 这三种元素含量的高低共同决定了不锈钢抗腐蚀、 抗氧化等性能^{[12, 13]}以及不锈钢的强度和硬度等性质^{[14, 15]}。 因此, 准确测量这三种元素的含量对于判断不锈钢合金是否具备所需特性至关重要。

然而, 尽管LIBS技术前景广泛, 但由于基体效应和自吸收效应等的存在, 导致光谱信号不稳定以及测量精度难以提升等问题, 在光谱数据处理过程中, 如何有效地选择和利用光谱中的关键特征是提高测量精度的关键之一。 传统方法中, 数据分析(例如峰值选择和波长分析)通常需要经验丰富的分析师的介入。 这些分析师需考虑单一参数或少量参数的相关性, 限制了分析的效率。 但随着机器学习(ML)算法的引入, 分析方式逐渐从根据经验进行建模分析过渡到了根据实验数据驱动分析^[16]。 ML工具的出现使得算法模型可以更容易地从采集到的光谱数据中提取更多信息。 赵文雅^[17]等归纳总结了LIBS结合神经网络(ANN)在地质、 合金、 有机聚合物、 煤炭、 土壤及生物等领域的具体应用, 并提出绝大部分ANN模型集中在BP 算法建立的网络模型 , 而其他 ANN 模型探索依旧很少, 有待更全面的研发。 Zhang^[18]等回顾了ML在LIBS中的研究现状和进展, 介绍了随机森林、 支持向量机、 人工神经网络等, 在介绍原理的同时指出了各种模型的特点, Brunnbauer^[19]等在讨论常见的用于LIBS的ML算法的原理和优点时, 还批判性地指出了常见数据处理方法的局限性, 包括部分算法的使用过程被视为‘ 黑匣子’ , 从而使结果无法得到很好的解释。 可以看出LIBS结合ML已经在多个领域得到了广泛使用, 但仍然存在进一步发展的空间。

虽然LIBS结合ML在元素量化上的效果相比于传统单变量分析法可以得到明显的提升, 但是构建ML模型不仅仅是将算法应用于数据集, 数据简化、 归一化、 特征选择以及超参数的优化缺一不可^[19]。 将原始LIBS全光谱作为ML的模型输入, 容易引发维度灾难, 导致模型过拟合, 模型分析精度较低。 相关研究人员提出多种特征选择方法以提取LIBS光谱中的有效信息, 已有研究包括主成分分析(PCA)^[20]、 独立成分分析(ICA)^[21]算法等降维或者特征选择方法与ML相结合用于待测样品元素的量化分析, 说明合适的特征选择可以在减小输入变量的同时保留有效信息, 最终提高模型的准确度。 变量重要性方法也是一种常见的特征选择方法, 可以评估ML模型中特征对模型性能的影响程度, 其原理根据不同的ML算法和度量方法而有所不同^[22]。 丁宇^[23]等应用变量重要性对RF模型的输入变量进行优化, 用于铝合金中镁(Mg)元素的定量分析, 结果表明相比于常规的RF模型, 基于变量重要性的RF模型在建模时间减少了91.67%的情况下预测精度也得到了明显提升。 除此之外, 还有多种特征选择算法在LIBS量化分析上也能实现改善模型性能的效果, Tavares^[24]等利用间隔连续投影算法(iSPA)选择变量, 结合PLS在预测土壤肥力属性上获得了最佳性能, 相比于全光谱输入的PLS模型, iSPA-PLS将变量数量最多减少了880倍。 Li^[25]等使用SBS算法消除LIBS谱中冗余或不相关的特征变量, 并基于筛选后的变量构建SBS-RFR标定模型, 在陶瓷样品多元素含量的测定中, 测定结果优于使用全光谱输入的PLS、 SVM和RF的回归模型。 Luarte^[26]等比较了先验知识结合四种变量选择算法用于铜精矿球团中铜(Cu)、 铁(Fe)和砷(As)浓度的LIBS测定, 包括KBest、 最小绝对收缩和选择算子正则化(LASSO), 主成分分析(PCA)和竞争自适应重加权抽样(CARS), 结果表明, 先验知识和LASSO的组合在综合性能指标和模型复杂性方面优于只使用先验知识和先验知识结合CARS、 KBest、 PCA。 这些方法旨在对光谱变量进行预处理, 以从复杂的光谱数据中选择最佳的特征子集, 提高特征变量和模型标签之间的关联性, 从而在实现降低计算复杂度的同时能够提高预测精度。 本文比较的顺序后向选择(SBS)、 LASSO两种特征选择方法应用于不锈钢样品中Ni、 Ti和Cr元素的量化分析尚未报道。

在本研究中, LIBS装置主要由激光器、 光谱仪、 时序控制装置和激光光路构成, LIBS光谱的采集过程在大气条件下进行。 所用激光器为灯泵浦紧凑型电光调Q激光器(Penny-300-TH), 激光波长为1 064 nm, 单脉冲能量约为40 mJ, 脉冲宽度10 ns, 激光频率为5 Hz。 为了实验数据的可靠性, 将3次剥蚀得到数据的平均值作为一次数据, 光谱仪为纳秒级曝光光谱仪(SR-750-B1, Andor Technology Ltd), 本实验使用的光栅为1 200 gr· mm^-1, 对应分辨率为0.04 nm, 带宽覆盖300~800 nm波长, 光谱仪的采集门宽设置为20 μ s, 采集延时设置1 μ s。 使用的探测器为增强型电荷耦合器件(ICCD), 型号为iStar 334T(Andor Technology Ltd), 具体实验装置示意图如图1所示。 激光光束经过扩束器扩束和反射镜反射后, 通过焦距为75 mm的会聚透镜聚焦在三维电动移动平台上的样品表面, 经由收光装置汇聚到光纤端面, 传输到光谱仪记录并转换, 最终在电脑上呈现并得到光谱数据。 本研究以不锈钢中的镍(Ni)、 铬(Cr)和钛(Ti)为待测元素, 7个不锈钢样品均购自钢研纳克检测技术股份有限公司, 编号序列为GBW01659a—01665a, 每个编号代表一个样品, 表1为样品中三种元素的参考含量。 为避免误差, 实验过程中每个样品选择20个不同的位置进行测量, 每个位置采集3次光谱得到平均值记录为一次数据, 共得到140条数据记录。 然后将得到的数据减去同条件下击穿空气时的光谱数据, 进行简单背景噪声去除。 利用该140条数据建立不同的校准模型, 分别使用全光谱数据、 SBS、 LASSO选择特征作为模型输入进行数据处理和定量分析, 以进行对比验证确定特征工程的分析效果, 使用Python(3.9.2版本)完成, 构建LASSO和SBS模型等主要使用了numpy、 pandas、 sklearn等库。

图1

Fig.1

	Figure Option ViewDownloadNew Window
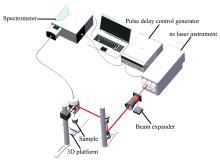	图1 纳秒激光诱导击穿不锈钢样品光谱实验流程图Fig.1 Schematic diagram of experimental process of nanosecond laser-induced breakdown spectrum of stainless steel samples

表1

Table 1

表1(Table 1)

表1 不锈钢标准样品中Ni、 Cr、 Ti元素浓度(U%为不确定度) Table 1 Concentrations of Ni, Cr, and Ti in standard stainless steel samples (U% is uncertainty) 编号 元素 Ni Cr Ti 含量 /% U /% 含量 /% U /% 含量 /% U /% GBW1659a 4.76 0.02 28.00 0.06 0.053 0.002 GBW1660a 14.58 0.03 14.37 0.03 0.475 0.005 GBW1661a 19.13 0.06 10.66 0.04 0.577 0.008 GBW1662a 11.24 0.05 19.73 0.05 0.253 0.004 GBW1663a 22.77 0.06 7.65 0.03 0.774 0.007 GBW1664a 7.34 0.04 24.40 0.07 0.170 0.004 GBW1665a 8.72 0.03 17.57 0.06 0.336 0.003

表1 不锈钢标准样品中Ni、 Cr、 Ti元素浓度(U%为不确定度) Table 1 Concentrations of Ni, Cr, and Ti in standard stainless steel samples (U% is uncertainty)

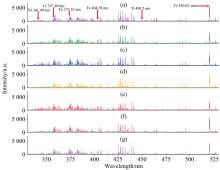
图2(a—g)是从7个不同样品(GBW01659a—01665a)中挑选出来的具有代表性的LIBS光谱, 采集的全光谱波长范围是300~800 nm, 由于光谱特征谱线主要集中在330~530 nm的范围中, 挑选特征谱线集中波段展示。 根据美国国家标准与技术局数据库确定不锈钢光谱中具有代表性物质元素的发射谱线并在图2中标出。 图中标识了三种标定元素Ni、 Ti、 Cr和基底元素Fe的部分特征发射谱线, 对比发现元素含量不同的不锈钢样品的发射谱线确实存在一定差异, 但是具体的量化情况难以直接分辨, 如果对光谱中的各个元素的特征谱线都进行标注, 工作量较大, 并且由于不锈钢样品中元素种类较多, 不同元素之间存在部分波长相近的特征谱线, 可能会导致针对标定元素选择的特征谱线受到其他元素的干扰, 从而无法在量化分析中起到有效作用, 因此需要采取适当的数据处理才能进行更准确的定量分析。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 激光(1 064 nm波长, 40 mJ能量, 10 ns脉宽, 5 Hz频率)诱导击穿不锈钢标准样品光谱 (a): GBW1659a; (b): GBW1660a; (c): GBW1661a; (d): GBW1662a; (e): GBW1663a; (f): GBW1664a; (g): GBW1665aFig.2 LIBS of standard stainless steel samples (1 064 nm wavelength, 40 mJ energy, 10 ns pulse duration, 5 Hz frequency) (a): GBW1659a; (b): GBW1660a; (c): GBW1661a; (d): GBW1662a; (e): GBW1663a; (f): GBW1664a; (g): GBW1665a

虽然在理论上光谱谱线强度与元素的含量呈线性相关, 但由于不同标样之间的成分差异较大, 受到元素间干扰、 自吸收以及激光能量波动等因素影响, 实际的光谱强度与元素含量往往呈非线性关系, 并且难以找到合适的特定谱线用于元素含量的预测^[17]。 而SBS算法是一种可以用于选择光谱波段的方法, 它允许从复杂的光谱数据中提取有用的信息, 以实现对元素含量的预测和分析。 其核心思想是从复杂数据中选择最具信息量的特征, 这些特征能够最好地反映标签的变化, 而忽略掉那些对预测没有帮助的特征^[27]。 这种特征选择可以显著提高元素含量分析的准确性, 并减少干扰因素的影响。 LASSO算法是一种用于特征选择和稀疏建模的线性回归技术, 通过正则化使原始特征稀疏化, 以保留对预测有贡献的特征, 从而实现特征选择。 为了比较不同特征处理方法的效果, 在将原始数据预处理后, 使用特征选择算法挑选特征, 与原始光谱和预处理光谱分别作为模型输入, 得到最终结果, 具体流程如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 激光诱导击穿光谱数据处理流程Fig.3 LIBS data processing

2.1 光谱预处理

对于LIBS样品, 除了不锈钢样品元素含量不同导致的差异外, 还有实验过程中产生的背景噪声辐射、 设备噪声、 模电转换过程产生的附加噪声等^{[28, 29]}。 因此需要采取光谱预处理方法以抵消无关信息, 从而提高模型的训练效果, 但是在LIBS中, 对于预处理方法并没有明确的偏好, 分析师采用的方法大部分都是对特定应用有效^[30], 因此本次研究中也提出多种预处理方案进行比较以确定最合适的方法。 本次实验选择最大最小归一化(MMN)、 标准正态变换(SNV)^[31]、 Savitzky-Golay平滑滤波(SG)^[32]以及内标法(IS)^[30]对光谱进行预处理, 通过对比决定系数R²和均方根误差RMSE以进行评估, 考虑到不同输入变量对模型的影响, 每一次预处理方法都会对模型参数进行优化以选择最佳模型。 R²和RMSE的表达式如式(1)和式(2)

$R^{2}=1-\frac{\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}$(1)

$\operatorname{RMSE}=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}$(2)

式(1)和式(2)中, n为样本数量, y_i是标准参考值, $\hat{y}_{i}$是对应的预测值。 R²是一种用于度量统计模型对观测数据的拟合程度的指标, R²越接近1, 表示模型对数据的拟合越好。 RMSE表示了模型的预测误差的标准差, 通常以与目标变量相同的单位来度量。 较低的RMSE值表示模型的预测与实际观测值更接近, 而较高的 RMSE 值表示模型的预测与实际观测值之间的差异较大。

预处理过程中使用的内标法为全谱内标法, 选取基底元素铁(Fe)在404.58 nm处的谱线强度对整个光谱谱线进行归一化处理, 归一化方法如式(3)

I'=IIFe(3)

式(3)中, I为降噪后的光谱数据, I_Fe为基体元素Fe在404.58 nm处的光谱强度, I'为归一化后的光谱数据。 最终对比效果如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于5折交叉验证的不同预处理方法对比Fig.4 Comparison of different pretreatment methods based on 5-fold cross-validation

与原始光谱相比, 所有预处理方法在Ti元素的含量预测上都有更好的性能表现, 在Ni和Cr元素中, 只有SG和IS模型性能有所改善。 并且无论是R²还是RMSE, SG平滑模型都具有最佳的表现, 以上分析表明对于定量分析不锈钢元素中Ni、 Ti、 Cr的含量, 本次实验中SG模型具有最佳的改善效果, Ni、 Ti和Cr的R²和RMSE分别为0.969 2、 0.957 9、 0.971 9和1.134 6 wt%、 0.044 2 wt%、 1.126 8 wt%。 可能是由于Ti元素含量较低, 光谱特征不突出, 所以大部分预处理方法过程主要都是在去除无关信息, 而Ni、 Cr元素的含量较高, 部分方法在去除不相关信息时也造成原始光谱信息的过度失真, 从而导致定量精度的降低。 在对比四种预处理方法和原始光谱后, 本次实验选择使用SG平滑预处理方法用于不锈钢样品中Ni、 Ti和Cr元素的分析。

2.2 特征选择

为了验证特征选择对于模型在不锈钢样品Ni、 Ti和Cr元素上的定量分析效果, 以SG平滑后的全光谱作为输入变量时, 构建偏最小二乘回归(PLS)模型和支持向量回归(SVM)模型并优化参数^[18], 在进行特征选择之前, 使用全光谱数据作为输入, 预测结果作为对比。 对于PLS模型, 最重要的参数是潜在变量数(LV), 通过五折交叉验证和网格搜索寻找最优潜变量数, 对于Ni、 Ti和Cr元素, 其最优潜变量数分别为4、 7、 5。 SVM模型的重要参数有两个, 分别是核函数(kernel)包括linear、 poly、 sigmoid、 rbf以及超参数C, 同样通过5折交叉和网格搜索寻找最优参数, 对于SG预处理后光谱的最终设置为, Ni: linear, C=0.58, Ti: poly, C=2.33, Cr: linear, C=0.38。 在后续特征选择完成后, 模型输入改变时, 会参考以上参数优化方式再次选择相应的最优参数。

2.2.1 SBS算法

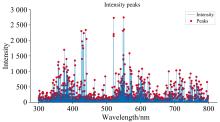
在理论上, LIBS光谱数据越多, 计算速度越慢, 本次实验的光谱数据中包含的离散点为33 994个, 属于高维度数据, 并且大部分为不相关或者冗余的特征变量, 在耗费大量计算资源的同时也会阻碍LIBS定量分析的精度。 本次实验采用的顺序后向选择(SBS)原理是按照变量的重要程度进行特征分类, 然后逐次迭代去除最不重要(重要性得分最小)的特征变量直到达到期望的特征变量个数。 由于原始数据包含33 994个离散点, 原则上应当从全光谱数据中使用排列组合选取最佳的特征组合, 从全光谱数据开始, 每次剔除一个最差的数据, 并记录此时最好的性能分数, 再进行下一次剔除, 最后选择性能分数最佳时的特征组合。 但由于数据点太多, 全部排列组合的数据量太为庞大, 计算效率低下, 因此考虑到光谱的有效特征绝大多数集中在谱峰中, 使用基于局部极大值的峰识别法, 设定窗口大小, 取窗口中的非边缘处的最大值为该窗口的峰值, 滑动一个数据点到下一个窗口再取峰值, 如果相邻的峰值相同则删除, 最终得到的为LIBS峰值, 在峰值提取过程中窗口的大小选择至关重要, 具体结果如表2所示。 当窗口大小设置为不大于10个数据点时, 峰值得到完全提取, 并且RMSE最小。 提取效果如图5所示。 将窗口设定为10时得到的光谱峰值作为SBS算法的输入变量。 使用PLS作为SBS算法的估算器, 质量指标为RMSE。 SBS算法的特征选择次数与RMSE值之间的关系如图6所示, 选择RMSE值最小时的特征组合, 选择的特征个数如表2 所示。

表2

Table 2

表2(Table 2)

表2 窗口大小对应特征选择个数和RMSE Table 2 The window size corresponds to the number of features selected and the RMSE 元素 窗口大小 选择特征个数 RMSE/wt% Ni 5 599 0.123 5 10 599 0.123 5 20 407 0.357 2 30 287 0.558 3 Ti 5 699 0.003 3 10 699 0.003 3 20 454 0.019 4 30 331 0.028 2 Cr 5 796 0.116 3 10 796 0.116 3 20 551 0.186 6 30 406 0.486 2

表2 窗口大小对应特征选择个数和RMSE Table 2 The window size corresponds to the number of features selected and the RMSE

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 LIBS光谱提取峰值示例(GBW1660a)Fig.5 Example of LIBS spectral peak extraction (GBW1660a)

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 窗口为20个数据点时SBS算法特征选择次数对应的预测性能Fig.6 Prediction performance corresponding to the number of feature selections of the SBS algorithm (windows=20)

2.2.2 LASSO算法

LASSO是一种广泛用于特征选择和稀疏建模的线性回归技术。 它在线性回归的基础上引入了L1正则化项, 通过最小化损失函数和L1正则化项的组合来实现特征选择和模型稀疏性^[33]。 L1正则化会使部分特征的系数变为零, 从而选择了最重要的特征, 而将其他特征忽略, 实现了特征的自动选择。 LASSO特征选择的关键在于添加的L1正则化项, 损失函数的表达式如式(4), 其中n为样本数, α 为常数系数, 需要进行调优, ‖ θ ‖ ₁为L1范数。 在LASSO算法中, 设定好正则化参数(即α )后会自动拟合回归模型, 生成预测值, 并将模型预测值与实际观测值进行比较, 得到RMSE。

J(θ)=12n(Xθ-Y)T(Xθ-Y)+α‖θ‖1(4)

在LASSO算法中, 需要对常数系数α 进行合适的参数调节。 对于本次采集不锈钢样品得到光谱数据, 针对Ni、 Ti、 Cr三种元素对常数系数的调节过程如图7所示。 当RMSE最小时, Ni、 Ti、 Cr对应的常数系数大小分别为0.2、 0.2、 2.65。 设置参数完成后, 将系数被稀疏为零的特征剔除, 剩余特征作为模型输入, 最终得到Ni、 Ti、 Cr的输入特征数量为852、 99、 134。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 LASSO算法参数调整对应预测性能Fig.7 LASSO algorithm parameters α Adjust corresponding prediction performance

2.3 结果对比

在完成输入变量的挑选和优化之后, 使用留一交叉验证法^[34]进行模型的训练, 即选取7个标准样品中的6个样品的实验数据作为校准集, 剩下1个样品的实验数据作为验证集, 循环7次, 得到每一组样品为验证集时得到的预测值, 将7组结果的评价指标再进行平均计算得到最终的评价指标, 采用R²、 平均相对误差ARE以及相对标准偏差RSD作为评价指标, ARE 用于衡量估算值相对于真实值的平均误差百分比, RSD是一种用于衡量数据集的相对离散程度的指标。 表达式如式(5)和式(6)

$\operatorname{ARE}=\frac{1}{n} \sum_{i=1}^{n} \frac{\left|\hat{y}_{i}-y_{i}\right|}{y_{i}}$(5)

RSD=1y̅1n-1∑i=1n(yi-y̅)2(6)

结果如表3所示, 总体来看, 无论是SBS算法还是LASSO算法选择的特征, 都能改善不锈钢样品Ni、 Ti、 Cr元素的预测精度, 表现最好的模型是SG-LASSO-PLS, 其中 Ni元素的ARE为3.50%, RSD为4.55%, Ti元素的ARE为2.66%, RSD为5.23%, Cr元素的ARE为0.93%, RSD为2.04%。 相比于全光谱数据, 无论是预测精度还是预测结果的稳定性, 都有较大的提升。 对于Ni和Cr元素, 最优预测结果的ARE均在4%以下, RSD也都在6%以下, 显示出较好的预测能力。 而SBS选择特征也能在预测精度上得到较大提升, 但是预测结果稳定性较差。 综上所述, 本实验的方法可以实现有效地预测不锈钢样品中Ni、 Ti、 Cr元素的含量, 从而对不锈钢的类型和性能进行评价。

表3

Table 3

表3(Table 3)

表3 不同输入变量在SVM和PLS模型的交叉验证结果对比 Table 3 Comparison of cross validation results of four input variables in SVM and PLS models 元素 模型 输入变量 ARE/% RSD/% Ni Full 12.25 4.56 SVM SBS 8.88 6.70 LASSO 7.48 4.29 Full 11.73 4.61 PLS SBS 3.53 5.68 Lasso 3.50 4.55 Ti Full 25.56 5.16 SVM SBS 22.70 5.00 LASSO 19.90 8.73 Full 10.77 5.40 PLS SBS 8.20 4.30 LASSO 2.66 5.23 Cr Full 5.90 3.70 SVM SBS 2.34 3.58 LASSO 2.01 3.15 Full 4.28 4.52 PLS SBS 2.76 3.78 LASSO 0.93 2.04

表3 不同输入变量在SVM和PLS模型的交叉验证结果对比 Table 3 Comparison of cross validation results of four input variables in SVM and PLS models

使用波长为1 064 nm激光剥蚀不锈钢标准样品, 得到多个LIBS光谱, 分别使用四种不同的预处理方法进行对比, 最终选择Savitzky-Golay平滑滤波法作为最佳预处理方法。 为对比不同特征选择方法对不锈钢样品元素含量预测的性能, 提出SBS算法和LASSO算法进行特征选择, 并与原始数据和经过SG平滑后的全光谱数据输入进行对比, 机器学习模型选择SVM和PLS。 最终结果表明, 本文提出的两种特征选择算法在有效降低模型输入变量的同时, 也显著提升了不锈钢样品元素的量化分析效果。 在分别采取SBS和LASSO选择特征后, 对比全光谱数据, 对于不锈钢样品中的Ni、 Ti、 Cr元素, 量化分析的准确度都表现出明显的提升, 并且LASSO算法还提高了预测结果的稳定性。 由此可见, 在不锈钢LIBS光谱的量化分析中, 对于Ni、 Ti、 Cr三种不同元素选择合适的特征选择方法, 可以表现出相对更加优异的预测性能, 实现对不锈钢Ni、 Ti、 Cr元素含量的快速准确预测。