作者简介: 王新强, 1977年生, 桂林电子科技大学光电工程学院正高级实验师 e-mail: xqwang2006@126.com
空间外差光谱技术(SHS)是一种新型的高光谱遥感探测技术, 被广泛应用于大气观测、 天文遥感、 物质识别等领域。 通过空间外差光谱仪获取的二维实测干涉数据会受到多种影响因素干扰, 其中高频噪声、 不规则暗斑、 干涉图非均匀性是其中最常见的影响。 这些影响会降低复原光谱的精度, 因此需要对这些影响发展有效的数据校正方法, 提高反演光谱准确度。 采用钾灯和氙灯两种光源产生准单色和连续光信号, 以它们形成的干涉数据作为研究对象。 针对这两种实测干涉图中的多种噪声影响, 提出了一种基于主成分分析的空间外差干涉数据校正方法。 首先采用一阶差分法对实测干涉图的所有行数据进行预处理, 去除基线影响, 将处理后的行数据进行傅里叶变换获得光谱数据。 然后对所有行光谱数据进行主成分分析, 计算出多个相互正交的主成分及每个主成分的贡献率, 将贡献率小于2%的主成分当作噪声并加以扣除, 保留其他主成分作为有效光谱信号进行光谱重建, 重建光谱经过傅里叶逆变换得到校正后的干涉图。 最后从干涉图和光谱两个维度对校正方法的有效性进行对比分析。 结果表明, 单色、 连续两种光源实测干涉图中的暗斑得到有效扣除, 非均匀性影响得到极大改善。 针对暗斑影响明显的干涉图第536、 600、 982行数据, 对比其光谱校正前后效果, 结果显示: 校正方法有效抑制了光谱中的高频噪声, 使光谱变得平滑、 清楚, 特征峰等细节获得凸显, 信噪比得到改善, 三行光谱的均方误差分别由校正前的0.037 77、 0.027 33、 0.030 99降低到校正后的0.013 31、 0.012 20、 0.012 34, 定量说明了方法的有效性。
Spatial Heterodyne Spectroscopy(SHS)is a new hyperspectral remote sensing detection technology widely used in atmospheric observation, astronomical remote sensing, material identification, and other fields. Two-dimensional measured interferometric data acquired by SHS can be interfered with by various influences, of which high-frequency noise, irregular dark spots, and interferogram nonuniformity are among the most common. These effects reduce the accuracy of the recovered spectra, and therefore, effective data correction methods need to be developed for these effects to improve the accuracy of the inverted spectra. In this paper, two light sources, potassium and xenon lamps, are used to generate quasi-monochromatic and continuous light signals, and the interference data formed by them are used as the object of study. A spatial heterodyne interferogram data correction method based on principal component analysis is proposed to address the effects of multiple noises in these two measured interferograms. Firstly, the first-order difference method is used to preprocess all the row data of the measured interferograms to remove the baseline effects, and Fourier transforms the processed row data to obtain the spectral data. Then, all the line spectral data are subjected to principal component analysis, multiple mutually orthogonal principal components and the contribution of each principal component is calculated, and the principal components with a contribution of less than 2% are treated as noise and deducted. In contrast, the other principal components are retained as valid spectral signals for spectral reconstruction, and the reconstructed spectra are inverse Fourier transformed to obtain a corrected interferogram. Finally, the effectiveness of the calibration methods is comparatively analyzed in terms of interferogram and spectral dimensions. The results show that the dark spots in the measured interferograms of monochromatic and continuous two light sources are effectively deducted, and the effect of non-uniformity is greatly improved. The effects before and after spectral correction are compared for the data in rows 536, 600, and 982 of the interferogram, which are affected by the dark spots. The results show that the correction method effectively suppresses the high-frequency noise in the spectra and makes the spectra smooth and clear, and the details of the characteristic peaks and so on are highlighted. The signal-to-noise ratio is improved, and the mean square error of the three rows of spectra decreased from 0.037 77, 0.027 33, and 0.030 99 before correction to 0.013 31, 0.012 20, and 0.012 34 after correction, respectively, which quantitatively illustrates the effectiveness of the method.
空间外差光谱仪具有体积小, 高光通量和高分辨率的特点, 对研究大气环境和天文遥感, 等领域具有重要意义[1, 2]。 在实际测量中, 空间外差光谱仪获取的原始数据为二维干涉图, CCD响应的非线性, 光学系统各器件表面或镜头沾染污渍等会使实测干涉图存在不规则的暗斑或者盲元, 直接对实测干涉图进行傅里叶变换会导致复原光谱失真, 需采用适当的算法进行校正处理。 Tarumi等提出了基于傅里叶变换干涉图直接分析的目标识别处理方法, 通过高斯带通滤波器对干涉图进行滤波消除背景以及噪声干扰, 该方法仅对单一吸收特征光谱有效, 不能处理多个连续吸收光谱[3]。 叶松等提出一种基于经验模态分解与回归分析的空间干涉谱目标提取方法, 可以从混合信号中提取出目标信号, 保留了钾共振双线特征峰, 抑制了旁峰的干扰, 但严重削弱了目标信号的强度[4]。
主成分分析[5, 6]是一种数据降维技术, 可以将线性相关的高维变量分解为线性无关的低维变量, 每个低维变量可以体现原始数据的某个特征。 通过提取部分低维变量, 可以从数据中获得所需的重要信息。 含噪声的干涉图中包含的信息可分为干涉条纹和噪声, 需要保留的信息为干涉条纹, 因此可以通过主成分分析算法, 提取代表干涉条纹的变量实现噪声去除。
本文根据空间外差光谱技术(spatial heterodyne spectroscopy, SHS)的基本原理, 针对单色光和连续光的实测干涉图中的不规则暗斑噪声和盲元, 提出了基于主成分分析法的校正算法, 从干涉图和光谱图两个角度分析算法的校正效果, 结果表明该算法对空间外差干涉数据有良好的校正效果。
空间外差光谱仪[7]是以空间调制的两束相干光干涉产生干涉图进而获取变换光谱的仪器, 它通过改变两束出射光的波面夹角来获得光程差、 实现干涉。 基本原理如图1所示。
当入射光通过光阑和准直透镜后形成平行光, 分束器将平行光分为强度相同的两束相干光, 相干光经过光栅衍射后返回到分束器, 产生干涉图, 最后由探测器记录二维干涉图数据[8, 9, 10]。 理想条件下二维干涉图每一行的数据相同, 一维表达式为
式(1)中, B(σ )为入射光谱, σ 为入射光波数, σ 0为系统Littrow波数, θ 为系统Littrow角, x为探测器像元位置。 干涉图数据I(x)与光谱数据B(σ )之间存在傅里叶变换关系, 干涉图经过傅里叶变换后可以获得光谱数据。
原始光谱数据中包含随机噪声与目标光谱, 其中随机噪声对原始数据的贡献较小, 可以通过将原始光谱分解为对原始光谱贡献不同的成分, 然后去除贡献较小的成分(随机噪声)实现光谱校正。 主成分分析[11, 12, 13]可以利用坐标变换将原始数据分解为贡献率不同的主成分, 本文根据主成分的累积贡献率, 选择相应的主成分进行数据重构, 从而提取光谱的有效信息。 因此, 可以利用主成分分析算法, 通过合理设置累积贡献率的阈值, 将含噪光谱中的光谱成分与噪声成分进行有效的分离。
对原始光谱数据进行主成分分析后, 可以获得原光谱所张成的线性空间的特征值及特征向量, 以及每个光谱在特征向量上的投影值。 其中, 特征向量代表一组新的正交坐标系, 投影值代表原始数据在新坐标系下的各分量值, 即主成分。 特征值λ i可以衡量第i个主成分包含的信息量, 特征值越大, 包含的信息越多。 对于含噪光谱数据而言, 某一主成分对应的特征值越大, 该主成分可以代表目标光谱信息越多。 为了直观表示每一个主成分包含的信息量, 需计算每个主成分的贡献率η i。 第i个主成分的贡献率可表示为
式(2)中, L为主成分的个数。 将所有主成分和特征值对应的特征向量按贡献率大小进行排序, 贡献率越大, 排名越靠前。 与噪声信号相比, 目标光谱信号的贡献率较大, 因此将贡献率大于阈值的主成分设为目标光谱信号, 通过提取贡献率大于阈值的前j个主成分, 得到目标光谱信号
式(3)中,
测试数据使用中科院安光所研制的空间外差光谱仪HEP-765-S采集, 该光谱仪的基频波长为756.5 nm, 光谱分辨率优于0.1 nm。 单色光光源采用北京曙光明电子光源仪器有限公司的空心阴极灯钾灯, 连续光光源采用西安超凡光电设备有限公司的GY-10高压球形氙灯。 搭建实验系统, 在暗室环境下使用空间外差光谱仪采集原始干涉图, 获得的钾灯干涉图和氙灯干涉图如图2所示。
 | 图2 实测干涉图 (a): 钾灯干涉图; (b): 氙灯干涉图Fig.2 Measured interferogram (a): Interferogram of potassium lamp; (b): Interferogram of xenon lamp |
两幅图像尺寸均为1 024× 1 024像素, 图中每一行代表一组一维干涉数据。 由图2可见, 两干涉图均存在强度分布不均匀现象, 部分区域存在形状不规则的斑点或斑块, 如红色方框内的数据, 这些影响的存在将降低复原光谱的准确度, 需要进行校正处理。
直接观察干涉图无法获知被测物质属性, 通常需要将干涉图转换为光谱图, 根据光谱信息判断被测物质。 原始干涉图中存在的直流成分会干扰光谱的复原, 可以采用一阶差分算法对原始干涉图进行去基线处理, 去除虚假低频信号。 干涉图与光谱图之间存在傅里叶变换关系, 对预处理后的二维干涉图进行傅里叶变换可以获得光谱数据。 本实验需要处理的二维干涉图包含1 024组一维干涉数据, 对每一组干涉数据采用傅里叶变换处理后可以获取1 024组光谱数据, 可表示为B=(b1, b2, , b1 024)T。
每一组光谱数据bi中包含两种信息, 即目标光谱和噪声光谱, 其中目标光谱信息为需要被提取的主要信息, 由于噪声光谱存在于可被探测的整个波长范围内, 无法通过简单的滤波处理进行去除。 主成分分析算法可以分析光谱数据中目标光谱与噪声光谱的相关性, 将目标光谱与噪声光谱分解为相互独立的成分, 进而通过保留目标光谱成分实现数据降维, 达到去除噪声的效果。 因此采用主成分分析算法对光谱数据进行校正处理, 具体步骤为: 首先计算原始光谱数据的均值(平均光谱), 对原始光谱规范化, 然后采用主成分分析算法对光谱数据B进行处理得到1 023个主成分S=(s1, s2, …, s1 023)。 将1 023个主成分的投影值si, 特征值λ i及特征向量vi按贡献率大小排序, 提取贡献率较大的前i个主成分作为目标光谱成分, 按上述理论中的式(3)进行光谱重建, 获取校正后的光谱图和干涉图。 对校正后的干涉图进行傅里叶变换, 得到校正后的光谱图。 提取剩余主成分作为噪声成分, 按相同的方式进行光谱重建获取噪声图。 通过分析校正后干涉图和光谱图中的噪声消除情况, 评价该算法的有效性, 具体流程如图3所示。
根据以上分析, 对原始干涉图进行去基线和傅里叶变换后, 得到1 024行光谱数据, 采用主成分分析算法对1 024组光谱数据进行处理, 并将每一个主成分的特征值, 特征向量和投影值进行排序, 其中前十个主成分的特征值, 贡献率和累计贡献率如表1所示。
| 表1 前十个主成分的特征值, 贡献率和累计贡献率 Table 1 The eigenvalue, contribution rate and Cumulative contribution rate of the first ten principal components |
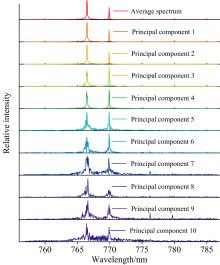
由表1可知, 前两个主成分比其他主成分的贡献率大且不是一个数量级, 累计贡献率达到96.422 9%, 平均光谱图和前十个主成分的光谱图如图4所示。
钾灯的两个特征峰为766.5和769.9 nm。 从图4可以看出, 在第一主成分和第二主成分中, 两个特征峰周围的噪声较小, 特征峰强度较大。 第三个主成分至第十个主成分中噪声逐渐增多, 每个主成分中的两个峰强度逐渐减弱, 且均不位于766.5和769.9 nm处, 说明在这些主成分中噪声已成为主要影响。
结合贡献率与光谱图分析, 按贡献率数量级以及光谱形状选取第一主成分和第二主成分作为钾灯光谱成分, 剩余主成分作为噪声, 分别进行光谱重建和傅里叶逆变换, 得到校正后干涉图, 如图5所示。
 | 图5 钾灯干涉图与噪声图 (a): 钾灯干涉图; (b): 噪声图Fig.5 Interferogram of potassium lamp and noise image (a): Interferogram of potassium lamp; (b): Noise image |
图5(a)与图2(a)对比可见暗斑噪声明显减少, 干涉条纹更加清晰, 光强分布更加均匀。 图5(b)中主要体现了噪声的贡献, 红色方框中标出的噪声与图2原始干涉图中的噪声对应, 表明通过保留前两个主成分可以很好地实现噪声的校正处理。
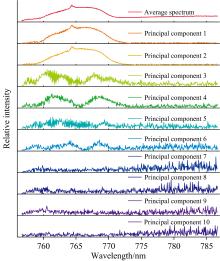
为了验证该算法对连续光的干涉图同样具有去噪效果, 对氙灯光谱数据进行相同的处理。 处理后的氙灯光谱数据中, 前三个主成分的贡献率分别为34.195%, 29.659%, 1.541%, 其中前两个主成分的贡献率均大于2%, 累计贡献率为63.854%, 平均光谱图与前十个主成分光谱图如图6所示。
由图6可知, 前两个主成分中氙灯特征峰强度较大, 第三主成分至第十个主成分中氙灯特征峰强度与噪声强度基本相同, 无法识别氙灯光谱的特征峰。 将贡献率大于2%的主成分, 即前两个主成分作为氙灯光谱成分, 其余主成分作为噪声成分, 分别进行光谱重建和傅里叶逆变换得到干涉图, 如图7所示。
 | 图7 氙灯干涉图与噪声图 (a): 氙灯干涉图; (b): 噪声图Fig.7 Interferogram of xenon lamp and noise image (a): Interferogram of xenon lamp; (b): Noise image |
从图7中可以看出, 图7(a)干涉图中噪声明显减少, 图7(b)为噪声图, 其中不规则形状暗斑噪声(红框内数据)已经被有效地分离出来, 说明该算法对连续光的干涉图也有良好的去噪效果。
为了进一步说明对光谱的校正效果, 选择500行噪声较小的干涉数据, 计算平均光谱并采用最小二乘法去基线, 作为真实光谱, 与校正前后干涉图的单行光谱图进行比较, 选取第536、 600、 982行进行展示, 这三行干涉图数据分别包含图2中三个红色方框中的噪声。 结果如图8所示。
 | 图8 氙灯单行光谱降噪效果图 (a): 第536行光谱; (b): 第600行光谱; (c): 第982行光谱Fig.8 Noise reduction effect of xenon lamp single line spectrum (a): Line 536 spectrum; (b): Line 600 spectrum; (c): Line 982 spectrum |
三行干涉图的校正前光谱如图8中红线所示, 噪声影响严重, 勉强可看出光谱大体轮廓, 其中的光谱细节已经无法分辨。 经过处理后, 蓝色三条光谱曲线均比较平滑, 光谱整体轮廓变得清晰, 765 nm附近的氙灯特征峰也清楚显现出来, 大部分噪声的影响获得去除, 同时可以进一步去除基线影响, 说明方法对单行数据校正效果也很好。
为了定量评价该算法的有效性, 计算这三行光谱校正前后的均方误差。 将图8中的平均光谱作为对比光谱, 结果如表2所示。
| 表2 氙灯光谱去噪前后的均方误差值 Table 2 MSE of xenon lamp spectra before and after denoising |
由表2可知, 三行光谱校正后的均方误差值均小于校正前的均方误差值, 也说明方法的校正效果较好。
提出的基于主成分分析的空间外差干涉图校正算法, 可以在保留干涉条纹信息的同时去除暗斑、 高频噪声, 改善干涉图的非均匀性影响。 首先通过对实测干涉图进行预处理和傅里叶变换获取含噪声的光谱数据, 然后采用主成分分析算法对光谱数据进行处理, 保留贡献率大于2%的主成分, 然后进行傅里叶逆变换, 得到校正后的干涉图。 最后进行傅里叶变换, 得到校正后的光谱。 研究结果表明: 通过算法处理后, 钾灯和氙灯的干涉图中噪声明显减少, 氙灯的三行光谱的均方误差均远小于去噪前的均方误差, 说明该算法对空间外差干涉数据具有较好的降噪效果。 但是在使用该算法时, 由于贡献率小的主成分直接被去除, 可能导致丢失部分有效光谱信息, 如何最大程度保留有效光谱信息仍需要进一步研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|