作者简介: 王方原, 1988年生, 桂林电子科技大学光电工程学院, 广西光电信息处理重点实验室副研究员 e-mail: wangfy@guet.edu.cn
拉曼光谱(Raman spectra)基于拉曼散射效应的散射光谱。 由于不同种类物质的振动、 转动能量特征是唯一的, 由此产生的拉曼散射光谱也是唯一的, 因此拉曼光谱在鉴别物质成分方面极具优势。 更因为无损耗、 非接触、 快速、 简单、 可重复等特点备受青睐, 被广泛应用于化学、 物理、 生物和医学等各个领域。 但受限于被测信号微弱、 光学仪器加工精度以及混合物组分之间的相互作用, 混合物的拉曼光谱不但存在谱峰重叠的现象, 部分较弱信号的特征峰还可能会淹没在背景噪声中, 影响了对混合物进行拉曼光谱分析的精度。 为了解决拉曼光谱弱信号分析识别的困难, 该研究将主成分分析应用于拉曼光谱分析, 提出一种基于全光谱信息的拉曼信号提取方法。 将实测拉曼光谱看作不同物质组分光谱的线性叠加, 通过不同组分比例的多组拉曼光谱进行主成分分析, 分离背景噪声和随机噪声并提取不同物质组分的拉曼信号。 根据物质组分拉曼光谱非必要满足正交性的特点, 分析讨论了光谱主成分与物质组分拉曼光谱成分之间的关系, 给出了采用光谱主成分修正为物质组分拉曼光谱的一般性方法。 根据光谱主成分与物质组分浓度之间的线性关联特征, 给出了物质组分拉曼光谱、 线性误差以及随机噪声的判定依据。 通过不同浓度的甲醇、 乙醇混合溶液拉曼光谱进行的实验验证, 实现了甲醇和乙醇拉曼信号的提取, 并成功分离了背景噪声和随机噪声, 最终结果与参考信号匹配良好, 同时验证了对物质组分拉曼信号、 线性误差以及随机噪声的判断结果。 提出了采用拉曼光谱主成分提取实际光谱组分的有效方法, 此方法具有快速方便, 成本低, 精确度高的优点, 是拉曼光谱数据处理技术的一种有益补充与尝试, 在物质识别和浓度检测方面具有极大的应用潜力。
Raman spectra are scattering spectra based on the Raman scattering effect. Since the vibration and rotation energy characteristics of different kinds of substances are unique, the resulting Raman scattering spectra are also unique. Raman spectroscopy is very advantageous in identifying the composition of substances. It is also favored for its lossless, non-contact, fast, simple, and repeatable characteristics and is widely used in various fields such as chemistry, physics, biology, and medicine. However, due to the weak signals measured, the processing accuracy of optical instruments, and the interaction between the components of the mixture, the Raman spectra of the mixture not only have the phenomenon of overlapping peaks but also some of the characteristic peaks of the weaker signals may be submerged in the background noise, which affects the accuracy of Raman spectroscopy analysis of mixtures. This study applies principal component analysis to Raman spectral analysis to solve the difficulty of analyzing and identifying the weak signals in Raman spectra. It proposes a Raman signal extraction method based on full spectral information. In this method, the measured Raman spectra are regarded as the linear superposition of the spectra of different material components, and the Raman signals of different material components are extracted through the principal component analysis of multiple Raman spectra with different component ratios, separating the background noise and random noise. According to the characteristics of Raman spectra of material components, which are not necessary to satisfy orthogonality, this paper analyzes and discusses the relationship between spectral principal components and Raman spectral components of material components and gives a general method of using the spectral principal components to be corrected to Raman spectra of material components. In addition, according to the linear correlation characteristics between the spectral principal components and the concentration of the material components, this paper also gives the basis for determining the Raman spectra of the material components, the linearity error, and the random noise. Through the experimental verification of Raman spectra of methanol and ethanol mixed solutions with different concentrations, the extraction of methanol and ethanol Raman signals is realized. The background noise and random noise are successfully separated. The final results match the reference signal well. The judgment results of Raman signals of the material components, linearity error, and random noise are verified simultaneously. In this paper, an effective method of extracting actual spectral components using Raman spectral principal components is proposed, which has the advantages of being fast and convenient, low cost and high accuracy, and is a useful supplement and attempt to the Raman spectral data processing technology, and has great potential for application in substance identification and concentration detection.
拉曼光谱[1], 是基于振动分子对光的非弹性散射的光学技术, 被誉为物质的指纹光谱[2]。 拉曼光谱具有操作简单、 测量时间短、 分析效率高等优点, 能够快速、 简单地提供被测样品的化学键、 相和形态、 结晶度等信息[3], 在生物学、 化学、 医学、 物理学等各个领域都有应用[4, 5, 6, 7, 8]。 在实际应用中, 特别是测量样本中含有多种组分物质时, 各种组分之间的拉曼信号相互叠加, 使得拉曼光谱的精细分析成十分困难[9, 10, 11, 12, 13, 14]。 快速和正确地识别及提取混合组分信号的光谱特征, 对于拉曼光谱分析的进一步发展非常重要。
为了解决上述问题, 目前主要存在两种方案, 分别是在实验中增强拉曼信号以及在数据分析过程中增强对混合信号的识别能力。 对于前者, 采用表面增强拉曼光谱(SERS)技术实现混合拉曼信号的选择性增强[15, 16, 17, 18, 19]; 对于后者, 通过机器学习对光谱进行定量分析可以实现拉曼光谱信号的识别和重构[20, 21]。 上述方法均有效提高了拉曼光谱的分析能力。 表面增强拉曼光谱只能增强特定化学结构的拉曼信号, 制备过程也较为复杂。 基于机器学习的光谱定量分析依赖于数据集的规模、 质量以及测量数据和数据集之间的关联性。 一种简单并且具有泛用性的拉曼光谱分析方法具有巨大应用前景。
主成分分析(PCA)是一种统计学方法, 能够将一组数据分解到不同的维度上。 每个维度上的数据都代表着当前信息丰富度最大的主成分, 主成分得分又可以反映主成分在原数据中的所占比例。 目前对拉曼光谱的研究中, PCA与机器学习相结合在样本分类的研究中取得了很好的效果[22, 23, 24, 25], 而采用拉曼光谱主成分提取各个组分光谱的理论方法还相对缺乏。 本研究聚焦采用主成分分析分离拉曼信号组分、 线性噪声和随机误差, 从而将不同未知物质组分的拉曼光谱信号一一准确提取出来。
本研究提出了一种基于主成分分析的拉曼光谱分析理论, 给出了主成分拉曼信号、 线性误差以及随机噪声的判定依据。 通过对具有不同浓度梯度的甲醇、 乙醇混合溶液的实测拉曼光谱进行分析, 提取了背景噪声以及甲醇、 乙醇的拉曼信号, 并根据光谱特征进行了去正交化操作, 准确恢复了甲醇和乙醇的拉曼光谱。 通过对修正前后的主成分得分与浓度的线性关联进行分析, 印证了对主成分中物质组分拉曼信号、 线性误差以及随机噪声的分析判断。 本方法成本低、 精确度高, 进一步扩展了对拉曼光谱进行主成分分析的方法, 完善了主成分分析应用于实测光谱的理论。
假设存在I种物质组分调配成的M份液体, 每份溶液的测量光谱都是由这I种物质组分的拉曼信号线性叠加得到, 各物质组分的浓度变化时仅使该物质组分的拉曼信号强度产生整体的线性变化, 而不改变特征峰的频率、 半高宽、 相对高度等参数。 第i种物质组分的拉曼光谱信号记作Ai(σ), 在不考虑误差的情况下, 测量得到的第m份液体拉曼光谱Bm(σ)可以表示为不同物质组分拉曼光谱Ai(σ)的线性叠加, 即
式(1)中, α mi是第m份液体中第i种组分所产生拉曼信号的强度系数。 如果溶液的份数M大于待测量的物质组分总数I(即M> I), 并且不同溶液根据式(1)得到的m个方程线性无关, 就可以通过主成分分析方法, 求出Bm(σ)中的各光谱成分Ai(σ)以及强度系数α mi。 (即主成分分析结果中的主成分及主成分得分)。
式(1)确定的线性叠加关系并不要求各拉曼光谱Ai(σ)严格满足正交性, 但主成分分析的结果中各主成分必须满足正交性。 测量光谱的主成分需要根据光谱特征进行一定的修正才能还原出所需要的物质组分拉曼光谱Ai(σ)。
如果考虑误差的影响, 则式(1)的线性叠加关系需要改为
式(2)中, Δ j(σ)表示第j种具有线性特征的误差(比如背景噪声、 系统误差等), β mj表示第j种线性误差在第m份溶液中的强度系数, ε m(σ)表示第m份溶液测量结果中的随机误差。 主成分分析的结果中, 各主成分是按照m个方程中线性关联程度从大到小排列。 因此线性关联误差Δ j(σ)与拉曼信号Ai(σ)在结果中都会被分解为光谱主成分, 并且随后可以根据误差与光谱的信号特征将两者区分。 而随机噪声ε m(σ)的线性关联非常弱, 因此在主成分分析结果中会排在最后。
通过用水、 无水乙醇与甲醇相互配比配制了一组浓度梯度相反的乙醇甲醇混合溶液, 即在乙醇浓度为5%, 10%, 15%, 20%, 25%时, 甲醇浓度分别为25%, 20%, 15%, 10%, 5%, 拉曼光谱测量设备采用北京杏林瑞光科技有限公司的RL-RP-785FS拉曼探头, 以及RL-SPEC光谱仪和NLM-785-IMF-(F)-500激光光源, 激发光的波长为785 nm, 激光功率约为800 mW, 每幅光谱的积分时间为5 s。 本研究的实验仪器及光路如图1所示。
实验测量结果如图2(a—e)所示。 标准乙醇溶液拉曼光谱在900、 1 050~1 150和1 300 cm-1以及1 470和2 800~3 000 cm-1处存在明显的特征峰, 标准甲醇溶液在1 040、 1 470和2 800~3 000 cm-1存在明显特征峰。 然而在混合溶液中, 各种组分之间的拉曼信号相互叠加, 甚至由于溶质浓度改变引起的化学环境变化, 对混合物的识别产生了较大影响。
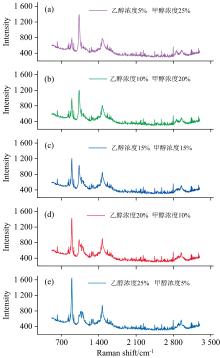 | 图2 不同浓度甲醇乙醇混合溶液的实测拉曼光谱Fig.2 Raman spectra of ethanol-methanol mixed solutions with different concentrations |
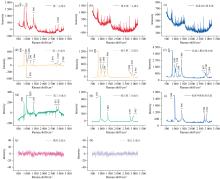
对图2中的5组混合溶液和水的拉曼光谱进行主成分分析, 得到的主成分以及与参考信号的对比如图3(a—k)所示。 第一主成分和水的实测光谱相似, 由于主成分分析结果中的各主成分必须满足正交性, 因此第一主成分中不可避免的存在其他信号的残余, 如在895 、 1 033、 1 466和2 945 cm-1处存在明显的特征峰, 而在最高浓度为25%的乙醇甲醇混合溶液的拉曼光谱中, 水和固定误差的信号强度最大, 因此第一主成分初步代表背景噪声。 第二主成分的特征峰主要与实测95%浓度的乙醇拉曼光谱特征峰对应, 890 cm-1附近特征峰由乙醇分子中C—C—O面内伸缩产生, 1 050~1 150 cm-1附近特征双峰由C—C—O面外伸缩产生, C—O—H弯曲振动产生了1 294 cm-1附近特征峰, 1 461 cm-1附近特征峰由CH3—不对称变形产生, 2 800~3 000 cm-1拉曼峰由—CH2, —CH3集团的对称、 不对称伸缩振动产生, 而在1 028 cm-1处, 存在一个与甲醇分子对应的明显倒峰并且呈现整体弯曲的状态。 第三主成分的特征峰与甲醇拉曼光谱的特征峰基本对应, 1 033 cm-1附近特征峰由甲醇分子中—CH3的非对称振动产生, 1 470 cm-1附近特征峰由C—H的弯曲振动产生, 2 800~3 000 cm-1的特征峰由C—H的伸缩振动产生, 而在890 cm-1处存在与乙醇拉曼光谱对应的特征峰并且整体弯曲。 第四主成分和第五主成分呈现明显的随机振荡, 代表随机噪声。 本实验的测量光谱实际为背景噪声、 乙醇光谱和甲醇光谱, 因此光谱理论上可以分解为三个互相正交的主成分(即第一至第三主成分)。 由于随机噪声的存在, 会对实测光谱产生扰动, 从而引入额外的主成分分量(第四和第五主成分)。 这些额外产生的“ 赝主成分” 通常对总光谱贡献较小(特征值小), 光谱呈现随机振荡, 并且与甲醇或者乙醇浓度变化没有线性关联。 至此初步判断含有有效线性成分的主成分有三个, 但是三个主成分中均含有拉曼信号和背景噪声不同程度的混杂, 需要进一步将其分离提取。
为了进一步修正这种由于主成分正交性(主成分严格正交, 而物质组分的拉曼光谱并不正交)而引入的信号混合, 实现采用主成分将拉曼光谱中不同成分提取, 需要根据光谱特征进行修正。 通常组分物质的拉曼信号由若干特征峰组成, 信号强度与组分物质浓度正相关, 非特征峰处的信号强度接近于零; 背景噪声(或者其他系统误差)对应的光谱形状保持稳定, 强度基本不随组分浓度发生改变, 通常表现为实测光谱的基线; 随机噪声通常表现为基准强度附近的随机振荡, 并且每次测量结果中的随机噪声不存在线性关联。 因此, 对所提取的主成分进行修正, 并于线性关联检验部分再次进行了验证。
分离步骤: 首先根据在1 000 cm-1处特征峰的大小计算补偿系数, 用第三主成补偿第二主成分的1 000 cm-1反常吸收峰。 其次根据890 cm-1特征峰计算补偿系数, 用补偿后的第二主成分消除第三主成分的890 cm-1特征峰。 然后采用补偿后的第二和第三主成分消除第一主成分的895和1 000 cm-1特征峰。 最后采用补偿后的第一主成分校准第二和第三主成分的基线弯曲。 至此根据1 000和890 cm-1处特征峰的信息, 通过前三个主成分的相互补偿, 得到了一个以890 cm-1处特征峰为代表的光谱[图3(e)]、 一个以1 000 cm-1处特征峰为代表的光谱[图3(h)]以及一个不包含上述两个特征峰的光谱[图3(b)]。 通过与标准参考光谱图3(c, f, i)的对比, 它们分别精确对应了标准甲醇乙醇、 标准甲醇光谱及背景噪声, 由此成功实现了物质组分拉曼光谱Ai(σ)的还原。
由于实测95%浓度甲醇溶液和乙醇溶液的浓度远高于分析所用的甲醇乙醇混合溶液, 并且在混合溶液中, 溶剂效应通常会导致分子振动频率的变化, 因此补偿得到的乙醇信号和甲醇信号与对应参考信号相比, 存在约10 cm-1的特征峰漂移现象。
已知不同浓度溶液数据的主成分得分(强度系数α mi), 其本质是主成分在某浓度溶液中的所占比例, 也代表着某浓度溶液在某主成分方向的投影, 因此在溶质浓度已知的情况下, 根据其主成分得分与物质浓度作图, 即可用主成分得分反映主成分在不同浓度溶液中的分布情况, 从而判断对拉曼光谱进行主成分分析提取不同物质的正确性。 而对于混合溶液, 由于主成分分析结果中的各主成分必须满足正交性, 各个主成分中存在其他信号的残余, 因此简单用主成分得分与物质浓度作图并不能反映各物质在不同浓度下的分布情况。 为了进一步验证各修正主成分所代表的物质组分的正确性, 要将修正后的主成分代入主成分分析表达式从而实现对主成分得分的修正。 修正前后的主成分得分与物质浓度如图4所示。 图4(a), (b)所示修正前后的主成分得分, 其纵坐标为主成分得分的强度, 下横坐标为乙醇浓度(Ethanol concentration), 上横坐标为甲醇浓度(Methanol concentration)。 所配置溶液为浓度梯度相反的混合溶液, 在乙醇浓度逐渐上升时, 甲醇浓度逐渐下降。
 | 图4 (a)主成分得分以及(b)修正后主成分得分与溶质浓度的线性关联Fig.4 (a) Principal component scores and (b) linear correlation between corrected principal component scores and solute concentration |
由图4(a), 第一至第三主成分随溶质浓度呈现线性变化, 但直线斜率与溶质浓度的对应关系并不特别显著。 第四和第五主成分随溶质浓度变化呈现出随机性的振荡, 说明信号强度与溶质浓度不存在线性关联, 因此它们属于随机噪声。 图4(b)中, 修正后的第一主成分得分随物质浓度变化的改变并不明显, 符合背景噪声的特性。 第二主成分得分随着乙醇浓度的升高具有明显的线性增加关系, 其线性相关系数为0.999 67, 符合乙醇信号在不同浓度的乙醇溶液中, 随浓度的上升强度不断增大的特征。 第三主成分得分随甲醇浓度的增加具有明显的线性下降关系, 其线性相关系数为0.999 71, 符合甲醇信号在不同浓度的甲醇溶液中, 随浓度的下降强度不断减少的特征。 这与上述对第一第二第三主成分进行修正后, 第一主成分代表背景噪声, 第二主成分代表乙醇信号, 第三主成分代表甲醇信号的判断相印证。
主成分得分的修正和主成分的修正相互印证, 不但证实了对主成分进行修正的准确性, 更可以采用主成分及修正后主成分得分和混合溶液浓度之间的强线性关联进行建模和预测, 在后续的研究中将进一步探究, 实现对低浓度多组分物质更精确的测量。
提出了一套基于主成分分析的拉曼全光谱分析理论, 并给出了主成分中物质组分拉曼光谱、 线性误差以及随机噪声的判定依据和提取方法。 通过对具有不同浓度梯度方向的甲醇和乙醇混合溶液进行实验和分析, 实现了甲醇和乙醇拉曼信号的提取, 分离了背景噪声, 验证了本方法的有效性。 根据修正后主成分得分与浓度的线性关联分析, 证实了对主成分中物质组分拉曼光谱、 线性误差以及随机噪声的分析判断, 再次证明了该方法的准确性, 完善了对混合溶液拉曼光谱进行主成分分析的全过程。 本研究成功实现了强背景噪声下拉曼弱信号的分离和提取, 得到了低浓度甲醇和乙醇光谱与使用高浓度溶液测得的“ 标准光谱” 相比存在几十个波数的特征峰漂移, 并且信噪比高于“ 标准光谱” 。 所提出这种新的基于全光谱主成分分析的拉曼信号提取方法, 对拉曼光谱混合信号的提取及多组分不同浓度物质的识别具有一定参考意义, 对极低浓度的拉曼光谱分析方法有待进一步探讨和研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|