臭氧是一种重要的大气痕量气体, 在大气化学和辐射过程中起着关键作用^{[1, 2]}。 大气臭氧可根据其在大气中的高度的不同而分为两部分: 高层平流层臭氧和低层对流层臭氧^{[3, 4]}。 对流层臭氧对人类健康、 自然植被生长产生不利影响; 平流层臭氧保护地球上的生命免受太阳有害紫外线的影响^[5]。 对流层臭氧主要由工业区氮氧化物和挥发性有机物光化学反应生成^[6]; 平流层臭氧主要在赤道地区生成并通过布鲁尔-多布森环流输送至高纬度地区^[7]。 20世纪70年代末, 南极洲地区上空臭氧空洞的形成对全球环境产生深远影响^[8]。 过去几十年里, 由于氟氯烃持续被释放到大气中, 每年春季在南极都观察到一个不断扩大的南极臭氧空洞^[9]。 为了解决臭氧空洞问题, 国际社会采取了一系列的措施, 其中最重要的措施是于1987年签署的蒙特利尔议定书(Montreal Protocol), 旨在逐步减少和禁止臭氧层破坏物质的生产和使用。 这一全球性的协议得到了广泛的支持和实施, 并取得了一定的成果, 臭氧层的破坏速度得到了放缓, 最近几年臭氧还有恢复的迹象^[10]。 臭氧层的修复是一个漫长的过程, 需要全球范围内的持续努力和合作^[11]。 全球臭氧观测日渐成熟^{[12, 13]}, 但连续一致的观测还有待解决。

探究区域气候变化与观测到的臭氧变化之间的相关性需要连续一致的臭氧总柱(total column ozone, TCO)记录。 此类记录有助于评估TCO的变化和长期趋势, 并为地球系统建模提供必要的数据。 自20世纪70年代末开始, 基于卫星的TCO观测已经可以在全球范围内进行, 并且具有高时间分辨率, 图1展示了国内外代表性臭氧监测卫星时间线。 其中FY-3系列和EMI系列是国内产品, 分别由长春光机所和安徽光机所制造。 各种卫星载荷提供TCO观测数据可以支持连续评估TCO的长期变化, 但是载荷设计、 仪器校准、 中心波长以及检索算法的差异对TCO观测结果产生跨载荷偏差。 据Kuttippurath等^[14]的研究指出, 不同载荷观测的TCO存在微小的跨载荷偏差, 也将对臭氧层恢复观测造成不利影响。 因此, 为了创建连续一致的TCO记录以评估长期臭氧变化, 我们需要尽量消除跨载荷偏差。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 国内外臭氧监测卫星时间线Fig.1 Timeline of domestic and international ozone monitoring satellites

一种可行的方法是对每个载荷的一级光谱数据进行校准, 以确保来自不同载荷的数据在通过相同的臭氧TCO算法之前是一致的^[15], 图2展示了大气痕量气体差分吸收光谱仪(environmental trace gases monitoring instrument 2, EMI-2)和对流层观测仪(TROPOspheric monitoring instrument, TROPOMI)太阳光谱。 这种方法准确度高, 因为避免了辐射校准非线性在TCO数据中产生的纬度和季节偏差。 8.6版本太阳后向散射紫外线(solar backscatter ultraviolet, SBUV)合并臭氧数据集(merged ozone data set, MOD)就是采用这种方法的代表性产品, 它提供了最长的、 基于单一仪器类型(即SBUV)的TCO观测数据^[16]。 对一级数据统一校正具有很高的准确性, 但建立不同载荷的一致校准工作量巨大, 并且只有与原始载荷团队合作才能实现, 显然是不可行的。 此外, 目前的8.6版SBUV MOD是一种分区的月平均网格化产品, 全球空间分辨率为5° , 其空间和时间分辨率不满足臭氧空洞的观测要求^{[17, 18, 19]}。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 EMI-2太阳光谱均值和TROPOMI 2023年6月18日单日太阳光谱Fig.2 EMI-2 average solar spectrum and TROPOMI solar spectrum for June 18, 2023

除了上述针对一级数据直接校正的方法, 针对二级TCO数据的统计偏差校正方法是消除跨平台载荷偏差的替代方案。 最常用的统计偏差校正方法包括简单的方法, 如增量变化和线性缩放^{[20, 21]}, 以及复杂的方法, 如非线性回归, 滤波^{[22, 23]}, 以及分布映射^{[24, 25, 26]}。 这些方法已被应用于校正气候模型的偏差, 但这些方法仍存在一些限制。 例如, 像增量变化和线性缩放这样的简单方法只解决了观察结果和模型输出之间的常见偏差, 这意味着这些方法无法处理具有依赖关系的非线性偏差。 神经网络这样的非线性方法的结果容易受到训练输入的影响, 如果训练输入没有覆盖足够的样本, 输出可能会产生偏差。 卡尔曼滤波法广泛用于预测过程中消除模型偏差, 但不能直接解决离散时间序列中的偏差, 因为这些偏差总是以连续的方式从先前的观察和预测中出现。 总的来说, 复杂的偏差校正方法, 如分布映射, 由于其自适应调整方案的表现比简单方法更好, 因此可以广泛采用^{[27, 28]}。 本工作采用重叠时间段内, EMI-2和TROPOMI跨载荷的TCO数据, 通过分位数-分位数(quantile-quantile, Q-Q)偏差校正方法将EMI-2数据同质化到TROPOMI水平^[29]。

将相同时间段EMI-2和TROPOMI的二级TCO观测结果生成连续一致的TCO记录。 再将世界臭氧和紫外线辐射数据中心(World Ozone and Ultraviolet radiation Data Centre, WOUDC)收集的地基TCO测量数据作为参考, 以评估偏差校正前后TCO记录的可靠性。

1.2 TROPOMI TCO数据

TROPOMI搭载于欧洲空间局(European Space Agency, ESA)设计的哨兵5(Sentinel-5 Precursor, S5P)卫星上, 于2017年10月发射。 哨兵5卫星过境时间为当地时间13:30。 TROPOMI有四个通道, 包括紫外线波段(270~320 nm)、 紫外可见波段(310~500 nm)、 近红外波段(675~775 nm)和短波红外波段(2 305~2 385 nm)。 其中紫外可见波段分辨率为0.55 nm。 TROPOMI的瞬时视场为114° , 相当于2 600 km的测绘带宽度, 可实现每日全球覆盖。

UVIS波段反演的TCO数据空间分辨率为5.5× 5.5 km², TCO的拟合波段为325~335 nm, 参考光谱为每日采集的太阳光谱。 上述方法在天底模式下, 电机需要每日转动采集太阳光谱, 对载荷的可靠性要求较高, 但最后反演结果偏差会减小。 空气质量因子也采用迭代AMF计算方法, 减少先验信息对最终AMF的影响^[36]。

表1

Table 1

表1(Table 1)

表1 EMI-2和TROPOMI详细仪器性能 Table 1 Parameters of EMI-2 and TROPOMI 参数 EMI-2 TROPOMI 光谱范围 UV1: 240~311 nm, UV2: 311~401 nm, VIS1: 401~550 nm, VIS2: 510~710 nm UV: 270~321 nm, UVIS: 310~500 nm, NIR: 670~775 nm, SWIR: 2 305~2 385 nm UV波段光谱分辨率 0.3 nm 0.55 nm 空间分辨率 13× 24 km2 5.5× 5.5 km2 视场角 114° 114° TCO拟合窗口波段 326~334 nm 325~335 nm 参考谱 月平均太阳光谱 日太阳光谱 AMF计算方案 迭代AMF计算 迭代AMF计算 UV波段光谱分辨率 0.3~0.6 nm 0.55 nm

表1 EMI-2和TROPOMI详细仪器性能 Table 1 Parameters of EMI-2 and TROPOMI

1.3 地基TCO数据

世界气象组织/全球大气观测网(World Meteorological Organization/Global Atmosphere Watch, WMO/GAW)建立的全球臭氧数据中心(WOUDC)中的地基TCO测量数据已被广泛应用于地面验证^[37]。 Brewer和Dobson分光光度计的TCO测量数据通常被用于验证卫星TCO观测值。 这两种仪器通过观测太阳辐射在特定波长的光谱辐照度来测量大气中的TCO, 主要依赖于紫外光谱中臭氧表现出强吸收特性的Huggins带的差分吸收理论^{[38, 39]}。

Brewer和Dobson仪器记录的TCO的精度都有很好的记录。 良好维护和校准的Dobson仪器通过直接观察阳光测量TCO, 估计的精度为1%, 对于太阳天顶角大于75° 的观察, 精度为2%~3%。 同样, 经过良好校准的Brewer仪器的偏差水平与Dobson仪器相当, 通过直接观察阳光的估计精度为1%。 尽管Brewer和Dobson仪器在性能上相似, 但由于使用不同的波长和臭氧吸收系数的温度依赖性不同, 仍然观察到± 0.6%的小差异^[40]。 本研究使用了2021年12月WOUDC档案中18台设备记录的TCO产品作为地面真值。

表2

Table 2

表2(Table 2)

表2 地基TOC数据的详细站点信息 Table 2 Detailed station information of ground-based TOC 站点名称 站点编号 纬度/(° ) 经度/(° ) 高度/m Hurghada 409 27.280 33.750 7 Linan 325 30.297 119.752 132 Xianghe 208 39.75 116.96 15 Longfengshan 326 44.727 127.585 334 Waliguan 295 36.287 100.898 3 810 Punta 473 -53.140 -70.850 22 Toronto 065 43.781 -79.468 202 Brisbane 027 -27.39 153.13 4.5 Macquarie 029 -54.50 158.95 10.0 Darwin 084 -12.42 130.89 30.4 Melbourne 253 -37.67 144.84 132.0 Gallegos 493 -51.601 -69.319 15 Tamanrasset 002 22.8 5.52 1 382 Marcapomacocha 429 -11.400 -76.330 4 500 Izana 300 28.309 -16.499 2 373 Seoul 252 37.57 126.95 84 New Delhi 010 28.65 77.217 220 Bangna 216 13.67 100.61 53

表2 地基TOC数据的详细站点信息 Table 2 Detailed station information of ground-based TOC

分位数-分位数(Q-Q)偏差校正方法通过获取相同时空内待校正观测结果和基准观测结果的累积分布函数(cumulative distribution function, CDF)之间的差异, 以去除每个待校正观测结果的偏差, 其中, 相关偏差是基于待校正观测结果和基准观测结果在CDF中显示的相同百分位数估算的。 这种方法已被证明在校准气候参数^[41]和降水^[42]的模型预测中是有效的。

图3展示了Q-Q偏差校正的原理, 实际数据的CDF形状差异较小, 四条线紧密相邻, 为了便于演示, 未使用实际数据CDF数据。 Q-Q偏差校正要求待校正观测结果和基准观测结果有着相同的输入时间段以保证准确的分布映射。 换句话说, 过去待校正观测结果是一个月的时间序列, 也应该保证基准观测结果也是一个月的时间序列。 把2021年11月EMI-2作为过去待校正观测结果, 则TROPOMI基准观测结果也应该是2021年11月。 一个在EMI-2观测时间序列中的TCO值obs_j(图3中的绿实线, 定义为原始观察, EMI-2结果记为obs_EMI-2)可以通过去除相关偏差校准到TROPOMI精度级别prj_j(图3中的蓝虚线, 定义为预测的TROPOMI观测结果, 记为prj_j)。 这个过程可以表示为

prjj=objj-ΔTCOj(1)

式(1)中, prj_j定义为预测的TROPOMI观测结果, obs_j定义为EMI-2原始观察结果。 Δ TCO_j定义为obs_j处EMI-2和TROPOMI之间的跨平台偏差。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Q-Q偏差校正方法示意图Fig.3 Schematic plot of Q-Q bias correction method

根据Q-Q偏差校正, 可以通过2021年11月重叠时间段EMI-2和TROPOMI的TCO观测值之间的分布映射来估算Δ TCO_j。 在这里, 跨平台校正整个过程如图3所示, 公式原理可总结如式(2)— 式(9)^[43]

$ \Delta \mathrm{TCO}_{j}=g \overline{\bar{\Delta}}+f \Delta^{\prime}{ }_{i}$ (2)

$ i=p \mid c_{C_{\mathrm{EMI}-2} \approx \mathrm{obj}_{j}}$ (3)

$ \Delta_{i}=C_{\mathrm{TROPOMI}}^{i}-C_{\mathrm{EMI}-2}^{i}$ (4)

$ \overline{\bar{\Delta}}=\overline{\overline{C_{\text {TROPOMI }}}}-\overline{\overline{C_{\text {EMI-2 }}}}$ (5)

$ \Delta^{\prime}{ }_{i}=\Delta_{i}-\overline{\bar{\Delta}}$ (6)

$ g=\frac{\overline{\overline{C_{\text {TROPOMI }}}}}{\overline{\overline{C_{\text {EMI-2 }}}}}$ (7)

$ f=\frac{\mathrm{IQR}_{C_{\text {TROPOMI }}}}{\mathrm{IQR}_{C_{\text {EMI-2 }}}}$ (8)

$ \operatorname{IQR}_{C_{\text {TROPOMI }}}=\left.C_{\text {TROPOMI }}\right|_{p=75 \%}-\left.C_{\text {TROPOMI }}\right|_{p=25 \%}$ (9)

式(2)— 式(9)中, C_EMI-2和C_TROPOMI分别表示EMI-2和TROPOMI的TCO观测结果数据集, 其中p表示C_EMI-2的CDF, i是p中C_EMI-2约等于obs_j的第i个百分位数, CiEMI⁃2和 CiTROPOMI表示C_EMI-2和C_TROPOMI第i个百分位数的观测值, $ \overline{\overline{C_{\mathrm{EMI}-2}}}$和$ \overline{\overline{C_{\text {TROPOMI }}}}$表示C_EMI-2和C_TROPOMI的中值, g和f是两个调制参数, IQR是四分位距(interquartile range, IQR), 即25%~75%。

上文中采用中位数而不是平均值的原因是避免由于可能存在较大的观测不确定性而导致的偏差传播。 此外, 分布映射一定是建立在相同的观测时间段, 才能消除跨平台偏差。

2.1 校正结果分析

图4(a)、 (b)和(c)分别是12月TROPOMI、 EMI-2和EMI-2均质化后的TCO数据, 三者一致性良好, 但是在中高纬度区域存在一定差异。 图4(d)、 (e)和(f)分别是12月EMI-2均质化前后TCO差值、 TROPOMI与EMI-2均质化前TCO差值和TROPOMI与EMI-2均质化后TCO差值, 从图中可以发现均质化前EMI-2与TROPOMI的TCO偏差较大, 但均质化后的EMI-2与TROPOMI的TCO偏差明显变小。 TCO偏差纬向分布较为均匀, 在中低纬度, 偏差较小, 在中高纬度偏差增大, 因为高纬度地区较大的天顶角会减弱光谱信号强度, 导致臭氧柱浓度反演结果偏差变大。 但经过均质化后, 大太阳天顶角对TCO的影响被有效地消除。

图4

Fig.4

Figure Option ViewDownloadNew Window

图4 (a) 12月TROPOMI平均TCO; (b) 12月EMI-2平均TCO; (c) 12月EMI-2均质化后平均TCO; (d) 12月EMI-2均质化前后TCO差值; (e) 12月TROPOMI与EMI-2 TCO差值; (f) 12月TROPOMI与EMI-2均质化后TCO差值Fig.4 (a) TROPOMI average TCO in December; (b) EMI-2 average TCO in December; (c) EMI-2 average TCO after homogenization in December; (d) TCO difference before and after EMI-2 homogenization in December; (e) TCO difference between TROPOMI and EMI-2 in December; (f) TCO difference between TROPOMI and EMI-2 after homogenization in December

图5是EMI-2均质化前后与TROPOMI数据的线性拟合结果, 拟合前在臭氧高值和低值区一致性较差, 低值不一致是由于南极地区太阳天顶角较大使探测器信号接受到的信号减弱, 高值区不一致也是北半球中高纬度较大的太阳天顶角所致。 TCO和TROPOMI相关系数R从未EMI-2均值化的0.960提升到均质化后的0.984。 均质化明显提升了散点图的线性, 减小不同观测系统的跨载荷系统偏差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
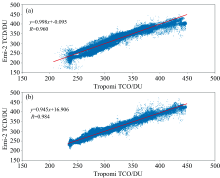	图5 (a) TROPOMI与EMI-2 TCO线性拟合; (b) TROPOMI与EMI-2均质化TCO线性拟合Fig.5 (a) TCO linear fitting of TROPOMI and EMI-2; (b) TCO linear fitting of TROPOMI and EMI-2 after homogenization

图5中使用的相关性和偏差公式如式(10)和式(11)

$R(X, Y)=\frac{\operatorname{Cov}(X, Y)}{\sqrt{\operatorname{Var}(X) \operatorname{Var}(Y)}}$(10)

BIAS=X-Y(11)

其中, X表示TROPOMI数据, Y表示EMI-2均质化数据, Cov(X, Y)表示X与Y的协方差, Var(X)与Var(Y)表示X与Y的方差, BIAS表示X与Y的偏差。

EMI-2均质化前后TCO和地面测量TCO之间的部分站点12月散点图如图6所示。 图中EMI-2均质化后TCO与地基TCO数据更加相近, 但也有少数点效果欠佳。 原因可能是使用地基单日平均数据作为基准与卫星某一时刻数据比较确实有待商榷, 但数据样本充足就能消除这一影响。 因此只要大多数均质化结果提升准确性, 同质化就是有意义的。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 六个站点地基TCO、 EMI-2原始TCO和EMI-2均质化TCO散点图Fig.6 Scatter plot of ground-based TCO, EMI-2 original TCO and EMI-2 homogenized TCO at six sites

图7中EMI-2均质化前TCO总体偏差低于5%, EMI-2均质化后TCO进一步提升数据准确性, 总体偏差低于3%。 有两个站点偏差较大, 11° S站点31天数据缺失22天, 22° N站点31天数据几乎没有波动, 这两个站点数据可靠性不够(不准确和数据缺失的站点较多, 图7中保留了两个有代表性的无效点留作说明)。 地基数据只有在较好的维护下才能准确, 总体而言, 欧洲、 北美与东亚地区地基站点维护较好。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 地基TCO与EMI-2原始TCO之间的相对偏差以及地基TCO与EMI-2均质化TCO之间的相对偏差Fig.7 Relative biases between the ground-based TCO and EMI-2 original TCO and relative biases between the ground-based TCO and EMI-2 homogenized TCO

值得一提的是在南极地区EMI-2原始数据准确性较TROPOMI更为准确, 但南极地基数据稀少, 站点维护困难, 并且由于高太阳天顶角, 数据准确性也难以保证, 所以上述结论难以证实。 EMI-2 TCO经过均质化后准确性提升, 均质化对全球长期一致的臭氧TCO观测有意义。

全球臭氧卫星观测已有四十多年, 星载臭氧总柱数据充足, 但受限于每颗卫星载荷的使用寿命, 无法做到四十多年连续观测。 基于数据充足, 但连续性差的现实, 各个卫星载荷之间数据均质化消除跨载荷系统偏差变得有意义。 运用Q-Q偏差校正方法对EMI-2 TCO数据进行均质化, 以达到TROPOMI级别的准确性, 并且均质化后的结果有助于臭氧的长期一致的观测。 联合观测时间为2021年11月, 再将2021年12月EMI-2的TCO数据均质化到TROPOMI级别。 经过分析, 均质化后的EMI-2的TCO数据与TROPOMI的TCO数据相关性R从0.960提升到0.984, 与地基数据比较均质化后的EMI-2的TCO数据偏差从整体低于5%降低到整体低于3%。 Q-Q偏差校正方法提高了EMI-2与TROPOMI数据的一致性, 降低了不同载荷之间跨载荷系统偏差。

本方法受限于EMI-2数据时间跨度, 无法做到与TROPOMI长期联合观测均质化。 未来数据充足, 使用几年的数据进行均质化, 并且用不同年份相同月份进行均质化, 将进一步消除EMI-2与TROPOMI数据的跨载荷系统偏差, 为全球臭氧长期一致观测做出贡献。