本研究区位于云南省普洱市墨江县农田区域, 墨江县位于云南省南部地区, 该地区雨水充沛, 年平均降水量1 388 mm, 光照充足、 干湿季分明, 年平均气温17.8 ℃, 年平均蒸发量1 696.7 mm, 属于南亚热带半湿润山地季风气候。 海拔478.5~2 278 m, 属于低纬度高海拔地区。 矿产资源丰富, 河流交错、 多高山深谷、 地貌复杂, 土地多为酸性土壤, 农田以山地为主。

土壤采样时间为2022年2月中旬, 土壤样品采集以农田土壤为主, 采集深度为0~20 cm。 在采样过程中采用GPS定位采样点位置, 并对采样点周围环境进行记录, 包括采样点经纬度坐标、 周围植被类型等, 土壤进行自然风干研磨过筛, 将土壤样品分为两份, 一份进行土壤Zn含量的测定, 另外一份进行土壤高光谱反射率的测定。 将60个土壤原始光谱采用Kennard-Stone(KS)算法将样本按照2∶ 1划分为建模集和验证集, 最终选取40个样本作为训练集, 20个样本作为验证集。

土壤的光谱反射率测定使用ASD FieldSpe c3 型便携式地物光谱仪(350~2 500 nm), 为减少其他光源的影响, 在可控光照条件的暗室内进行土壤高光谱数据的测定, 将获取的高光谱数据利用Savitzky-Golay(SG)法对原始高光谱曲线进行平滑处理。 大量研究表明对光谱进行一阶导数变换能提高模型精度^{[10, 11, 12]}, 因此为减少噪声干扰, 更好的消除基线效应, 有效的突出光谱特征, 对平滑后的光谱曲线(R), 分别进行一阶导(R')、 倒数的一阶导(1/R)'、 对数的一阶导(logR)'、 平方根的一阶导$(\sqrt{R})^{\prime}$四种不同数学变换。

二维光谱指数相对于一维光谱预处理的优势在于可以更充分地利用光谱数据中的信息, 一维预处理只考虑了光谱数据中的一个维度, 而五种优化光谱指数对350~2 500 nm波段范围内任意两波段进行两两组合, 顾及到了多个光谱维度之间的关系以及高光谱波段之间的相互影响, 可以进一步突显出波段之间的隐藏信息, 从而可以更全面地描述光谱特征, 并获取相关性更高的光谱特征波段, 基于五种光谱指数, 即归一化指数(NDI)、 差值指数(DI)、 比值指数RI、 和指数(SI)、 倒数差值指数(IDI)对四种数学变换下的光谱进行两两组合运算从而构建优化光谱指数, 光谱指数公式如表1。

表1

Table 1

表1(Table 1)

表1 优化光谱指数及其公式 Table 1 Spectral indices and formula Spectral index Formula Normalized difference index(NDI) NDI(λ i, λ j)= R(λi)-R(λj)R(λi)+R(λj) Difference index(DI) DI(λ i, λ j)=R(λ i)-R(λ j) Ratio index(RI) RI(λ i, λ j)=R(λ i)/R(λ j) Sum index(SI) SI(λ i, λ j)=R(λ i)+R(λ j) Inverse difference index(IDI) IDI(λ i, λ j)= 1R(λi)- 1R(λj)

表1 优化光谱指数及其公式 Table 1 Spectral indices and formula

1.5.1 反演模型

采用偏最小二乘(PLSR)与多元线性回归(MLR)模型作为土壤Zn含量的反演模型。 偏最小二乘法可以很好地解决多重共线问题, 处理变量数大于样本数的数据^[13], PLSR在高光谱分析中得到广泛应用^{[14, 15]}。

多元线性回归模型(MLR)用于描述一个变量与多个变量的关系, 与简单线性回归模型不同, 多元回归模型把多个解释变量纳入模型, 可以同时考虑多个因素对因变量的影响, 从而避免重要因素被遗漏而导致构建的模型产生较大的误差。

1.5.2 精度评价

结合建模决定系数( Rc2)、 预测决定系数( Rp2)、 校正均方根误差(RMSEC)、 预测均方根误差(RMSEP)、 相对分析误差(RPD)评价模型精度。 R²的计算结果越接近1, 表示模型能够较好地解释观测数据的变化, 拟合效果越好。 RMSE表示模型预测值与实测值之间的差异, 用于衡量模型的预测精度。 RMSE的计算结果越小, 表示模型的预测精度越高, 预测值与实测值的差异越小。 RPD用来描述模型的预测性能, 当RPD≥ 2时, 表示模型的预测能力很好; 当1.4≤ RPD< 2时; 表示模型的预测能力一般。 当RPD< 1.4时, 表示模型的预测能力较差, 则模型不能进行预测。

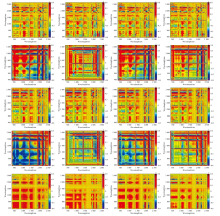
将R'、 (1/R)'、 $(\sqrt{R})^{\prime}$、 (logR)'不同数学变换形式下的光谱分别进行光谱指数运算, 然后将计算得出的指数值与土壤Zn含量实测值进行相关系数的计算, 得到相关系数二维矩阵数据, 并绘制出土壤归一化指数(NDI)、 差值指数(DI)、 比值指数(RSI)、 和指数(SI)、 倒数差值指数(IDI)高光谱矩阵系数图, 如图1(a— t)所示。 通过比较矩阵系数图可知NDI与DI图以对角线为界上下两部分关系系数相反, 而SI与IDI图上下两部分关系系数相同, 既相互对称, 若二维相关性等势图上下|r|对称, 则最高|r|相同, 最佳波段组合相同。 而指数RI矩阵系数图上下部分|r|并不对称, 这是由不同指数的公式属性所导致, 基于指数DI与SI、 IDI所得到的较高相关系数数量显著多于指数NDI与RI, 说明相对于指数NDI与RI, 经过指数DI与SI、 IDI的计算更能突出更多与土壤Zn敏感状况相关的光谱有效信息, 能够较大程度提高与土壤Zn含量的相关性。

图1

Fig.1

Figure Option ViewDownloadNew Window

图1 不同形式光谱指数与土壤Zn含量的相关矩阵图 (a): NDI-R'; (b): NDI-(1/R)'; (c): NDI-( R)'; (d): NDI-(logR)'; (e): DI-R'; (f): DI-(1/R)'; (g): DI-( R)'; (h): DI-(logR)'; (i): RI-R'; (j): RI-(1/R)'; (k): RI-( R)'; (l): RI-(logR)'; (m): SI-R'; (n): SI-(1/R)'; (o): SI-( R)'; (p): SI-(logR)'; (q): IDI-R'; (r): IDI-(1/R)'; (s): IDI-( R)'; (t): IDI-(logR)'Fig.1 Correlation matrix diagram between different forms of spectral indices and soil Zn content (a): NDI-R'; (b): NDI-(1/R)'; (c): NDI-( R)'; (d): NDI-(logR)'; (e): DI-R'; (f): DI-(1/R)'; (g): DI-( R)'; (h): DI-(logR)'; (i): RI-R'; (j): RI-(1/R)'; (k): RI-( R)'; (l): RI-(logR)'; (m): SI-R'; (n): SI-(1/R)'; (o): SI-( R)'; (p): SI-(logR)'; (q): IDI-R'; (r): IDI-(1/R)'; (s): IDI-( R)'; (t): IDI-(logR)'

通过比较NDI、 DI、 RI、 SI、 IDI在R'、 (1/R)'、 $(\sqrt{R})^{\prime}$、 (logR)'不同数学形式光谱变换下与土壤Zn含量的相关性, 选出最大相关系数绝对值波段组合, 如表2所示, 除了经过(1/R)'变换下的SI及IDI指数与Zn含量最大相关系数绝对值小于0.7以外, 其他最大相关系数绝对值均大于0.7, 光谱指数在经过不同的数学变换后均不同程度提高了与土壤Zn含量之间的相关性。 从指数层面看, 基于NDI指数在上述几种数学变换下最大相关系数绝对值均为0.756, 最优组合波段均为(2 284, 2 291), 同时NDI在上述几种数学变换下所得到的最大|r|均大于0.75, 表现较为突出。 指数DI、 SI及IDI在经过R'变换后均得到最大|r|, 分别为0.749、 0.730、 0.770, 最佳波段组合为(2 301, 2 283)、 (1 924, 2 168)、 (2 001, 683), 经过(1/R)'变换后计算得出的RI指数最高|r|为0.729, 对应的最佳波段组合为(2 268, 2 337)。 从数学变换形式方面看, 在经过R'变换后除指数RI外其他指数最高|r|均大于或等于其他数学变换形式所得出的最高|r|, 说明与其他三种数学变换相比R'可以进一步突显光谱隐含信息。 并且表2显示土壤Zn的各数学变换下的优化光谱指数最佳组合中的波段主要为1 908、 1 924、 2 168、 2 208、 2 268、 2 283、 2 284、 2 291、 2 301、 2 337, 所得到的波段基本在前人研究得到的范围内^[16]。

表2

Table 2

表2(Table 2)

表2 任意两波段光谱指数与土壤Zn含量相关系数最大值及最佳波段组合 Table 2 The maximum correlation coefficient and optimal band combination between spectral indices of any two bands and soil Zn content spectral index R' (1/R)' (logR)' $(\sqrt{R})^{\prime}$ r band combination r band combination r band combination r band combination NDI 0.756 (2 284, 2 291) 0.756 (2 284, 2 291) 0.756 (2 284, 2 291) 0.756 (2 284, 2 291) DI 0.749 (2 301, 2 283) 0.702 (1 597, 2 131) 0.710 (2 437, 2 208) 0.738 (2 301, 2 283) RI 0.712 (1 924, 2 168) -0.729 (2 268, 2 337) -0.728 (2 134, 2 337) -0.728 (2 134, 2 310) SI 0.730 (1 924, 2 168) 0.680 (2 208, 2 193) 0.716 (2 268, 2 337) 0.719 (2 268, 2 337) IDI 0.770 (2 001, 683) 0.665 (1 871, 2 036) 0.715 (1 908, 2 168) -0.731 (1 908, 2 155)

表2 任意两波段光谱指数与土壤Zn含量相关系数最大值及最佳波段组合 Table 2 The maximum correlation coefficient and optimal band combination between spectral indices of any two bands and soil Zn content

单变量特征波段在建模方面相对二维光谱指数所需要的光谱波段会更多, 通常需要效果较好的特征选择算法来挑选建模所需要的光谱特征波段, 增加了实验复杂性, 而利用光谱指数来构建模型输入变量则可用最少的光谱波段得到最佳的反演模型。 分别选择在R'、 (1/R)'、 $(\sqrt{R})^{\prime}$、 (logR)'不同数学变换下所构建的光谱指数与土壤Zn含量相关性绝对值最高的五个光谱指数值作为模型的输入变量。 采用PLSR和MLR进行建模, 结果见表3。 在同一数学变换形式下输入光谱指数值相同时PLSR所构建的模型精度要高于MLR, PLSR模型在处理多重相关性自变量, 能更好地进行敏感信息的筛选, 进而能提高模型预测精度。 以同一建模方法, 当输入变量为数学变换(1/R)'时所得的光谱指数值时, 模型精度高于R'、 $(\sqrt{R})^{\prime}$、 (logR)'。 R'~PLSR模型有相对较高的 Rc2=0.68、 Rp2=0.75和相对较低的RMSEC=6.68 mg· kg^-1和RMSEP=6.05 mg· kg^-1, 其预测性能较好(RPD值大于1.8), 但比(1/R)'~PLSR模型精度有所降低, 在多元回归模型方面基于MLR~(1/R)'的模型精度也较好(RPD值> 1.8), 但相对于(1/R)'~PLSR与R'~PLSR模型RPD分别降低了0.18与0.07。 其他五种模型预测能力一般, RPD值均介于1.53~1.66之间, 模型对土壤Zn含量的估计有限。 (1/R)'~PLSR模型RPD> 2.0说明模型预测能力很好, 因此在(1/R)'光谱变换下得到五种优化光谱指数相关系数绝对值最高, 五个光谱指数值结合PLSR能够获取光谱与土壤Zn含量之间更有效的信息并实现对土壤Zn含量的精准估算。

表3

Table 3

表3(Table 3)

表3 土壤Zn含量估算模型精度结果对比 Table 3 Comparison of accuracy results of soil Zn content estimation models Spectral transformations Model Modeling set Validation set Rc2 RMSEC/(mg· kg-1) Rp2 RMSEP/(mg· kg-1) RPD R' PLSR 0.68 6.68 0.75 6.05 1.98 MLR 0.75 5.94 0.60 7.09 1.59 (1/R)' PLSR 0.61 7.45 0.77 5.07 2.09 MLR 0.63 7.24 0.73 5.54 1.91 $(\sqrt{R})^{\prime}$ PLSR 0.66 6.89 0.61 6.60 1.59 MLR 0.66 6.88 0.59 6.72 1.57 (log/R)' PLSR 0.64 7.14 0.64 6.55 1.66 MLR 0.65 7.05 0.57 7.00 1.53

表3 土壤Zn含量估算模型精度结果对比 Table 3 Comparison of accuracy results of soil Zn content estimation models

为了更加直观地对比PLSR和MLR模型, 基于PLSR与MLR的最佳土壤Zn含量实测值和预测值的散点图如图2(a, b)所示, 在1∶ 1散点图中, 样点越接近于1∶ 1线, 预测值就更接近于实测值, 模型预测的结果越精确。 通常模型实测值与预测值点大多集中于1∶ 1直线附近, 当验证集中有个别样点Zn含量较小时, 验证点则会偏离1∶ 1线, 随之模型精度会受到不同程度的影响。 相对于其他预测模型, (1/R)'~PLSR模型所得到的验证集拟回归直线与1∶ 1直线的夹角最小, 说明该模型的数据拟合能力相对于其他模型有一定程度的提高。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于PLSR与MLR的土壤Zn含量实测值和预测值的散点图 (a): PLS-(1/R)′, (b): MLR-(1/R)′Fig.2 Scatter plot of measured and predicted soil Zn content based on PLSR and MLR (a): PLS-(1/R)′, (b): MLR-(1/R)'

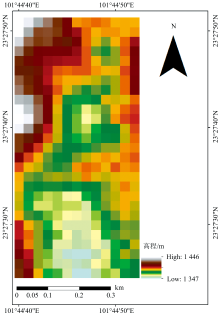
采用2.2节选出的最佳土壤Zn含量预测模型所得到的预测值结合克里金插值法绘制土壤Zn含量空间分布图, 由图3可以看出, 预测结果图中部土壤Zn含量较高, 并呈现出由中间向四周逐渐降低的趋势。 由图中可知土壤Zn含量预测值在35.1~74.5 mg· kg^-1, 此外研究区属于农田区域, 而云南省农田土壤Zn含量背景值为89.70 mg· kg^{-1 [17]}, 可以看出土壤Zn含量在整个研究区内都没有超过背景值, 说明研究区农田并未被土壤重金属Zn污染。 图4为研究区高程图, 从东西两边看, 地势从中间向两边逐渐增高, 从北到南高程逐渐降低, 研究区中部有三处低洼地形。 土壤Zn在上游水流长时间的作用下发生移动, 并在低洼处沉积, 因此土壤Zn在研究区中部有三处地方Zn含量相对其他地方较高, 此外研究区为农田, 农药和化肥中有微量的Zn元素, 随着农业的发展农药和化肥的使用也是造成土壤Zn含量研究区中部土壤Zn含量较高的原因之一。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 土壤Zn含量的预测值空间分布图Fig.3 Spatial distribution of predicted soil Zn content

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 研究区高程Fig.4 Elevation map of the research area