引用本文
郭洪旭, 王龙, 杨凯, 吴凡, 邓一荣, 唐长城, 陈志良, 肖荣波. 土壤Cr含量高光谱反演模型组合优化研究[J]. 光谱学与光谱分析, 2024,44(11): 3273-3279.
GUO Hong-xu, WANG Long, YANG Kai, WU Fan, DENG Yi-rong, TANG Chang-cheng, CHEN Zhi-liang, XIAO Rong-bo. Research on Combination Optimization of Hyperspectral Inversion Model for Soil Cr Contamination[J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3273-3279.
Doi:10.3964/j.issn.1000-0593(2024)11-3273-07  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
土壤Cr含量高光谱反演模型组合优化研究
郭洪旭1, 王龙1, 杨凯1, 吴凡1, 邓一荣2, 唐长城1, 陈志良3,*, 肖荣波1,*
1.广东工业大学, 广东 广州 510006
2.广东省环境科学研究院, 广东 广州 510045
3.生态环境部华南环境科学研究所, 广东 广州 510535
*通讯作者 e-mail: chenzhiliang@scies.org; ecoxiaorb@163.com

作者简介: 郭洪旭, 1984年生, 广东工业大学副教授 e-mail: guohx@163.com

收稿日期: 2023-08-27 修回日期: 2024-03-15
基金: 国家自然科学基金-广东联合基金重点项目(U1911202), 科技部重点研发计划项目(2019YFC1805300), 广东省自然科学基金项目(2019A1515012131)资助
摘要

土壤重金属污染高光谱反演的特征波段提取方法和反演模型的选择是影响反演精度的关键; 二者如何优化组合, 提高反演精度是目前亟需解决的难题。 在华南典型铬(Cr)污染区, 采集了92组土壤样品, 使用电感耦合等离子体质谱(inductively coupled plasma mass spectrometry, ICP-MS)检测Cr含量, 并使用ASD Field Spec4地物光谱仪在实验室收集其高光谱信息。 光谱信息预处理采用平滑滤波(SG)+标准正态化(SNV)+二阶微分(SD)变换组合, 减弱土壤散射和噪声的影响。 选择竞争性自适应重加权采样(CARS)、 逐步投影算法(SPA)、 无信息变量消除(UVE)、 遗传算法(GA)四种算法提取特征波段。 选择多元线性回归(MLR)、 偏最小二乘法(PLSR)、 支持向量回归(SVR)和人工神经网络(ANN)四种反演模型建立特征波段与Cr含量之间的关系。 通过对比不同特征波段提取方法和反演模型组合对土壤Cr含量反演的结果发现: 采用CARS和UVE特征波段提取方法可以显著提高PLSR、 MLR和SVR模型的预测效果; SPA方法能够提高ANN模型的预测效果; 通过SG+SNV+SD+CARS+PLSR组合方式, 提取位于800~1 000、 1 400~1 700以及2 100~2 450 nm之间的98个特征波段, 建模后模型验证, 决定系数 R2为0.97, 均方根误差RMSE为5.25 mg·kg-1, 平均绝对误差MAE为4.35 mg·kg-1, 相对分析误差RPD为3.94, 表明该模型在预测土壤Cr含量具有优异的性能。 以土壤Cr污染高光谱反演为例, 通过比较不同特征波段提取方法与反演模型组合的反演精度, 确定最优模型, 为小样本土壤重金属污染反演的建模提供了思路。

关键词: 高光谱; 模型组合优化; 特征波段选择; 反演模型
中图分类号:TP79 文献标志码:A
Research on Combination Optimization of Hyperspectral Inversion Model for Soil Cr Contamination
GUO Hong-xu1, WANG Long1, YANG Kai1, WU Fan1, DENG Yi-rong2, TANG Chang-cheng1, CHEN Zhi-liang3,*, XIAO Rong-bo1,*
1. Guangdong University of Technology, Guangzhou 510006, China
2. Guangdong Academy of Environmental Sciences, Guangzhou 510045, China
3. South China Institute of Environmental Science, Ministry of Ecology and Environment, Guangzhou 510535, China
*Corresponding authors
Abstract

The accurate inversion of soil heavy metal pollution in hyperspectral analysis relies on carefully selecting characteristic band extraction methods and inversion models. Finding the optimal combination of these two factors to achieve the highest system inversion accuracy remains an urgent and essential problem in this field. The present study involved the collection of 92 sets of soil samples from a typical Chromium (Cr) contaminated area in South China. The Cr content was quantified using Inductively Coupled Plasma Mass Spectrometry (ICP-MS). Additionally, the ASD Field Spec4 Spectrometer was employed to gather hyperspectral information in the laboratory. The spectral information preprocessing employed the combined SG+SNV+SD method. Here, SG refers to the Savitzky-Golay smoothing filter, SNV stands for Standard Normal Variate normalization, and SD represents second-order derivative transformation. This combined methodology was employed on the unprocessed spectral data to diminish the impact of soil scattering and noise. Consequently, it enhanced both the quality of spectral data and the precision of feature analysis. Four algorithms, namely Competitive Adaptive Reweighted Sampling (CARS), Successive Projections Algorithm (SPA), Uninformative Variable Elimination (UVE), and Genetic Algorithm (GA) were employed to extract Characteristic bands. Subsequently, the relationships between the extracted Characteristic bands and Cr content were established by using four inversion models: Multivariate Linear Regression (MLR), Partial Least Squares Regression (PLSR), Support Vector Regression (SVR), and Artificial Neural Network (ANN). A comparative analysis of various Characteristic band extraction methods and combinations of inversion models regarding their impact on the accuracy of soil Cr content inversion determined that the SG+SNV+SD preprocessing enhances the spectral data's capability to represent characteristic information. CARS and UVE Characteristic band extraction methods can significantly enhance the predictive performance of PLSR, MLR, and SVR models. In contrast, the SPA method improves the predictive effectiveness of the ANN model. Through the combination approach of SG+SNV+SD+CARS+PLSR, a total of 98 characteristic bands located within the ranges of 800~1 000, 1 400~1 700, and 2 100~2 450 nm were extracted. Model validation yielded an R2 value of 0.97, RMSE of 5.25 mg·kg-1, MAE of 4.35 mg·kg-1, and RPD of 3.94. These evaluation metrics demonstrate the exceptional predictive capability of the model for soil Chromium Cr. In this research, soil Cr pollution was selected as a case study for hyperspectral inversion. A comparative analysis of various combinations of characteristic band selections and inversion model methods identified the optimal approach for modeling the inversion of heavy metal pollution in representative soils characterized by limited sample size and high contaminant concentrations.

Keyword: Hyperspectral; Model combination optimization; Feature band selection; Inversion model
引言

铬(chromium, Cr)是土壤中常见的污染物, 具有危害性强, 迁移过程复杂等特征, 是城乡土壤污染防治关注的重点[1]。 高光谱遥感由于无损检测、 操作便利等优势, 成为快速调查土壤重金属污染状况的新技术之一[2]。 由于Cr的光谱特征较为微弱, 因此采用不同的数理统计方法进行Cr元素的光谱特征提取和反演建模, 已成为当前土壤Cr污染定量反演研究的热点之一。

目前高光谱定量反演主要包括预处理、 特征波段选择、 反演模型构建三个阶段。 光谱信息易受环境和样品背景影响, 采集的光谱反射数据存在干扰信息, 这些干扰信息会降低建模效率和影响模型精度。 因此对光谱数据特征波段的提取和干扰信息的剔除是定量反演模型构建的前提, 对简化模型和提高模型稳健性有关键作用。 研究表明竞争性自适应重加权采样(competitive adaptive reweighted sampling, CARS)、 逐步投影算法(successive projections algorithm, SPA)、 无信息变量消除(uninformative variable elimination, UVE)、 遗传算法(genetic algorithm, GA)等波长选择算法可以提升模型的反演效果[3]。 土壤光谱数据通过特征波段筛选后, 结合土壤污染物浓度数据进行定量反演模型构建, 而模型的正确选择是影响反演精度的关键。 常用的反演模型有统计分析模型和机器学习算法模型两类。 统计分析模型具有结构简单、 参数少、 过程相对容易的特点。 例如, 多元线性回归(multivariate linear regression, MLR)可以描述多个自变量与因变量之间的线性关系[4]; 偏最小二乘法(partial least squares regression, PLSR)是多元线性回归模型的一种变形, 在建模过程中注重主成分分析、 典型相关分析和线性回归分析方法的特点, 目前已经有大量研究证明PLSR在多元线性分析中的可行性[5]。 在多参数、 多类型、 非线性、 复杂映射关系的定量反演中, 机器学习算法模型如支持向量回归(support vector regression, SVR)和人工神经网络(artificial neural network, ANN)等具有更优越的性能, 并在土壤湿度遥感定量反演中已得到广泛应用[6]。 ANN是一种模仿人脑神经细胞结构和功能的系统。 由于ANN具有强大的非线性映射能力, 它在许多领域得到了广泛应用, 并取得了令人满意的结果[7]。 SVR主要优点是可以很好地解决小样本、 非线性和高维的模式识别问题, 并可应用于其他机器学习问题。 特征波段的提取方法和建模方法的选择是影响模型反演精度的前提。 现有研究在确定最佳特征波段提取方法时, 通常选取一种常用反演模型, 依据模型反演精度, 确定最优特征波段提取方法。 张霞[8]等通过构建土壤Cd含量的PLSR模型, 反演结果对比认为CARS算法相对于相关系数法和遗传算法特征选择有更高的精度; 涂宇龙[9]等利用主成分分析和皮尔逊相关性分析分别对Cu元素进行特征波段选择, 并使用逐步回归法进行建模, 发现PCA特征提取后重金属Cu含量反演精度更好。 为了确定最佳建模方法, 通常是固定一种特征波段提取方法, 比较多种建模方法的反演精度, 选出最佳模型。 安柏耸[10]等通过连续小波变换(continuous wavelet transformation, CWT)提取土壤光谱特征波段, 通过PLSR、 反向传播神经网络(back propagation neural network, BPNN)、 随机森林(random forest, RF)和SVR方法构建土壤重金属镉含量估测模型, 发现CWTR’ -SVR方法在镉浓度预测方面表现最佳, 决定系数(R-Square, R2)和均方根误差(root mean square error, RMSE)分别为0.86、 0.02 mg· kg-1; Zhao[11]等比较了MLR、 BPNN和BPNN(GA-BPNN)遗传算法优化三种模型估算Hg浓度性能, 发现GA-BPNN模型效果最佳, R2、 RMSE分别为0.923、 0.042 mg· kg-1。

尽管随着高光谱反演土壤重金属含量研究的发展, 利用多种特征波段选择算法优化同一模型和探索一种特征波段选择算法对不同模型的优化的研究日渐增多。 但特征波段的提取方法与反演模型的不同组合, 对模型反演精度的影响仍有很大研究空间。 由于各种实验条件和土壤组分之间存在巨大差异, 很难通过文献统计来准确比较不同波段选择算法与不同模型之间的最优组合。 因此确定特征波段提取方法和定量反演模型之间的最佳组合, 逐渐成为实现系统最优反演精度的重要议题。 为了比较常用波段选择方法和反演模型的不同组合对土壤重金属含量反演精度的影响, 以华南典型Cr污染区为研究对象, 通过多步预处理减少环境噪声对数据的影响, 应用四种常用特征波段提取方法提取特征光谱信息, 建立四种线性和非线性Cr含量预测模型, 比较不同特征波段提取方法与建模方法组合对模型反演精度的影响, 确定最优组合, 为土壤重金属反演提供合理的建模思路和方法。

1 实验部分
1.1 数据采集

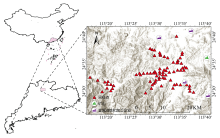
研究区(图1)中心地理位置位于113° 33'00″E, 24° 33'06″N, 气候属亚热带季风气候区, 夏季盛行西南季风和东南季风, 冬季受东北季风影响, 年降雨量1 400~1 900 mm。 韶关地区的主导土壤类型以红色土壤为主, 这种土壤因其富含氧化铁而呈现出鲜明的红色或棕红色调, 是该区域的一种重要土壤类型。 该地区地处矿山附近, 拥有大量冶炼厂和重金属加工等金属结构制造企业, 是我国典型的重工业密集分布区, 土壤重金属污染问题突出[12]。 该地区的农田、 建设用地、 工矿企业及相关人类活动主要分布在低海拔平原地区。 以农用地为研究对象, 围绕污染企业和农用地的空间关系, 在典型污染企业下风向, 选择典型样地采样。

图1 研究区与样本采样点Fig.1 Study area and sampling sits

通过均匀布点方法共采集92个点位土壤表层(0~20 cm)土样, 风干研磨过20目筛, 并平均分为两份土壤进行实验室Cr浓度测量和光谱测量。 土壤Cr浓度由电感耦合等离子体质谱仪测定, 具体方法是将土壤样品先经硝酸-盐酸-氢氟酸微波消解后定容摇匀, 再直接用电感耦合等离子体质谱仪测定Cr的含量。

土壤光谱测量是在暗室中使用美国ASD(Analytica Spectra Devices., Inc)公司生产的FieldSpec4现场光谱分析仪测量, 其光谱波段范围为350~2 500 nm, 共包含2 151个波段。 室内光谱测量条件如下: 开始测试前, 仪器预热30 min, 使用白板矫正。 完成校正后, 将过筛后的土壤样本均匀铺放在黑色消光布上, 轻轻按压, 保证样本表面平整。 采用1 000 W卤素灯带作为光源, 照度与垂直方向成30° , 光源与样本距离30 cm。 光谱探头垂直放置在样本表面上方, 距离样本表面5 cm。 每个样本在4个方向(旋转3次, 每次90° )进行测量, 每个方向保存10条光谱曲线, 取平均值作为样本的分析光谱数据。 所有样本按照上述步骤, 逐一测定。

1.2 光谱预处理

光谱预处理主要用于消除光谱数据无关信息和噪声, 使其更好地符合数据分析的目标。 采用平滑滤波(Savitzky-Golay, SG)消除光谱信号中的噪声, 并通过标准正态变量变换(standard normal variate, SNV)消除固体颗粒大小、 表面散射以及光程变化对漫反射光谱的影响, 修正由于样本大小以及环境等因素带来的谱线偏移[13]。 最后采用光谱的二阶微分(second derivative, SD)进行基线偏移校正, 减少误差对模型精度的影响, 提高光谱信息中不同官能团的特征信息表征能力。 考虑到单一的预处理方法效果有限, 因此采用SG+SNV+SD的组合进行数据预处理。

1.3 特征波段选择

对光谱数据进行特征波段选择, 可剔除光谱数据冗余信息, 并且可以降低数据维度, 集中分析那些对目标物质的测量具有较高敏感性的波段。 由于选取的特征波段具有与目标变量的相关性, 因此模型的预测结果更容易解释和理解[6]。 使用了CARS[2]、 SPA[14]、 UVE[13]、 GA[15]四种常用算法进行特征波段选择, 通过交叉验证进行参数设置, 并对每种算法进行了十次运行, 以获得最佳的结果, 减小随机性对结果的影响。

1.4 反演模型选择

采集的土壤光谱数据中, 有部分重复样本, 需要选取代表性强的样本来建立校正模型, 提高建模速度、 减少模型库的储存空间。 考虑到浓度变量和光谱信息的影响, 采用光谱-理化值共生距离(sample set partitioning based on joint x-y distance, SPXY)算法将土壤光谱样本划分出训练样本74个, 验证样本18个。 将提取的特征波段反射率数据作为自变量, Cr浓度作为因变量, 进行定量反演模型构建, 为了对比MLR、 PLSR、 SVR[16]、 ANN[17]四种常用定量反演模型, 通过实验数据对模型调试后, 确定各模型的最佳参数设置。 其中, SVR模型使用linear核函数, gamma参数设置为1× 10-7, ε 采用默认值 0.05, 通过网格法确定惩罚系数C值为2进行构建; ANN选择Sigmoid作为激活函数, trainlm作为训练函数, 设置两层隐藏层, 第一与第二隐藏层均为20个神经元, 设置参数为: 最大迭代次数为2 000, 训练目标最小误差为0.001, 学习效率为0.05, 其余参数均为默认值。

1.5 模型精度评估

所有数据处理与算法构建均由MATLAB代码进行实现(图2)。 模型精度由决定系数R2、 均方根误差RMSE、 平均绝对误差(mean absolute error, MAE)、 相对分析误差(relative percentage difference, RPD)四个参数衡量。 决定系数R2的取值范围是[0, 1], 数值越大表示预测值和测量值之间的线性关系越强, 模型的稳定性越高。 均方根误差RMSE用来衡量观测值与预测值之间的偏差。 模型的RMSE值越小, 表示模型的预测准确度越高, 偏差越小, 即模型的预测能力越强。 MAE表示观测值与其算术平均值之间的绝对偏差的平均值。 较小的MAE值表明模型具有更好的预测能力。 相对分析误差RPD用于比较预测模型的性能。 较大的RPD值表示较小的误差和更好的性能。 当RPD≥ 2.0时, 表示模型具有可靠性; 当1.5< RPD< 2.0时, 表示模型相对可靠, 但可以通过其他方法进一步提高模型的可靠性; 而当RPD≤ 1.5时, 表示模型不可靠。

图2 数据处理与算法构建流程Fig.2 Data processing and algorithm construction process

2 结果与讨论
2.1 Cr含量的描述性统计分析

数据集包含了92个样本, 土壤Cr含量的最小值为0 mg· kg-1, 最大值为139 mg· kg-1, 平均值为48.67 mg· kg-1, 中位值为45 mg· kg-1, 标准差为29.23 mg· kg-1, 变异系数为58.88%(表1), 表明样本中土壤Cr含量离散程度大, 研究区Cr含量空间异质性强。 同时, 土壤Cr含量的平均值高于广东省表层土壤、 中国表层土壤的平均值[18]。

表1 土壤Cr含量描述性统计分析 Table 1 Soil Cr content descriptive statistical analysis
2.2 土壤光谱反射率特征

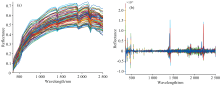
在实验室条件下, 测量了92个Cr污染土壤样本的高光谱相对反射率曲线[图3(a)]。 观察结果显示, 土壤的反射率光谱在可见光至红外波段呈现逐渐增强的趋势, 并未出现明显的反射峰或吸收峰, 峰-谷变化微弱。 在波长为1 400、 1 900和2 200 nm处, 我们发现经过烘干的土壤光谱仍然具有三个明显的水吸收带。

为了提高模型的预测精度, 对原始光谱数据进行了SG+SNV+SD的预处理。 通过预处理, 各土壤样品之间的光谱反射曲线差异减小。 在水吸收谷附近, 出现了极值, 而在350~500、 1 400~1 500、 1 800~1 900以及2 000~2 300 nm波段之间显示明显的差异。 在其他波段间, 光谱曲线重合度较高。 结合图3(a)和(b)可以发现, 通过一系列的预处理, 可以增强光谱信号, 减少噪声和干扰, 从而更清晰地显示出光谱中的特征。

图3 Cr污染土壤原始相对反射率曲线(a)和预处理后相对反射率曲线(b)Fig.3 Original relative reflectance spectra (a) and pretreatment relative reflectance spectra (b) of Cr-contaminated soil samples

2.3 预处理对模型反演精度的影响

预处理对于提高SVR和MLR建模的精度具有显著作用。 使用SG+SNV+SD预处理后建立模型, SVR、 PLSR和MLR的精度均有所提升。 SVR模型的改善幅度最为显著, R2值从0.33提高到0.78; PLSR模型的R2值从0.60上升到0.64; 而ANN模型的精度略有下降(表2), 其R2为负值这可能与模型过度拟合或模型参数不合适。

表2 不同预处理方式的建模结果 Table 2 Modeling results of different preprocessing methods
2.4 不同特征波段选择方法与反演模型组合对反演精度的影响

使用SG+SNV+SD方法对原始光谱数据进行预处理后, 选择四种特征波段选择方法提取重金属Cr的光谱响应波段, 组合MLR、 PLSR、 SVR、 ANN四种模型建模(表3)。

表3 特征波段方法与反演模型的不同组合的建模结果 Table 3 Modeling results of different combinations of feature band method and inversion model

CARS、 SPA、 UVE和GA四种算法分别选出98、 16、 347以及995个波段, 其中CARS、 UVE与GA三种算法提取的波段数量多, 这可能与特征波段选择算法参数设置和高光谱数据波段数量多有关, 选择的特征波段之间可能存在一定的相关性(表3)。 通过特征波段选择算法后, 波段数量减少一个数量级, 降低了无效信息对建模的影响。 对比表2和表3可知, 预处理结合特征波段选择进行建模的反演效果显著提升。 其中, SG+SNV+SD+CARS的建模精度最高, PLSR、 SVR、 MLR模型的验证R2均超过0.93, RMSE和MAE均小于7.5, 低于Cr浓度一个数量级, RPD均大于2, 说明此方法建立的模型精度更高、 模型更稳定可靠。 SG+SNV+SD+UVE也显著提升了PLSR、 SVR、 MLR、 ANN建模精度。 SPA算法对ANN模型精度有显著提升。 其中最显著的SG+SNV+SD+CARS+SVR, 其R2相对于原始数据建模方式提升了1.8倍、 RPD提升了1.4倍, RMSE和MAE也大幅提升, 模型精度和可信度更高。

通过对比各种组合的预测精度, 显示光谱数据预处理后进行特征波段选择, 降低因变量的数量, 能够显著提升定量模型的预测精度。

2.5 特征波段选择与预测结果

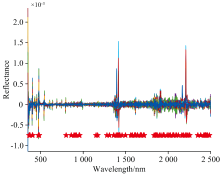
对光谱数据进行SG+SNV+SD方式预处理后, 四种特征波段选择算法对模型预测精度的影响不同。 利用选择特征波段效果最好的CARS算法提取出98个特征光谱带(图4), 主要集中在400~500、 800~1 000、 1 300~1 700以及2 100~2 450 nm之间, 这与已有Cr高光谱反演选择出的波段范围400~600、 1 300~1 500及2 000~2 200 nm基本吻合[19], 说明CARS对光谱信息特征波段的选择能力突出, 具有推广潜力。 这可能与CARS算法在进行波段选择时考虑了光谱角度, 并且算法具有自适应性和竞争机制, 能够适应性地调整各波段权重和通过不同波段的相互竞争, 最后选出对目标变量更加敏感的敞段。

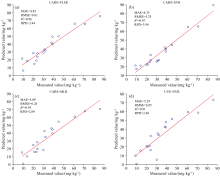
图4 通过CARS选择的特征光谱带Fig.4 Feature spectral bands selected by CARS

通过各种组合处理建模后, 有四种R2较好的模型(图5)。 在验证集18个样品中, Cr含量最低为9 mg· kg-1, 最高为86 mg· kg-1, 平均浓度37 mg· kg-1。 样本中Cr浓度跨度较大, 部分极值可能对建模精度有影响。 而通过CARS处理后, MLR对各阶段浓度的拟合比较好, SVR与PLS模型中, 高浓度的偏离程度较大一些, 但三种模型的拟合结果相当好, CARS+SVR/PLS/MLR预测值最接近真实值其中误差2~4 mg之间。 而SPA+ANN(R2=0.77)在中高浓度间的预测值严重偏离真实值, 预测效果较差。 由于CARS算法主要基于蒙特卡洛采样方法, 因此其选择的特征波段信息对线性模型PLSR和MLR的建模效果提升更大, 由于本研究中的SVR模型核函数为线性核函数“ Linear” , 因此其模型验证结果优于ANN模型。 此外, 本研究样本量较小, 神经网络的训练结果较差, 线性模型PLSR预测能力优于非线性模型ANN, 对于SVR模型在小样本较高特征维度数据的表现非常优秀, 但在小样本较低特征维度数据的表现很差, 而PLSR模型整体反演效果比较好, 因此如果数据集较小, PLSR可能更容易建立稳健的模型[5]。

图5 4种最佳模型组合拟合结果Fig.5 Fitting results of the 4 best model combinations

3 结论

通过四种波段选择算法对华南地区土壤样本光谱数据进行处理, 提取特征波段, 简化了计算并且提高了建模精度, 利用Cr浓度和特征波段信息进行MLR、 PLSR、 SVR、 ANN四种模型的构建和精度比较, 发现不同的特征波段选择方法和建模的组合的反演精度不同。

(1)经 SG+SNV+SD预处理后的光谱, 预处理和特征波段选择能够显著提高SVR、 MLR 的建模效果, 而这两种方式对ANN建模方式没有正向作用。 通过SNV和SD处理后的光谱更利于建立适用于小样本模型, 原始光谱反射率经过SG+SNV+SD处理后能够放大350~500、 1 400~1 500、 1 800~1 900和2 000~2 300 nm之间的细微差异, 提高特征信息表征能力。

(2)CARS和UVE算法可以有效剔除与Cr污染无关的光谱波段, 提取适合模型构建的特征波段数据, 有助于减少光谱维度和提高模型精度。 由于CARS、 UVE算法都是基于线性回归的原理提取特征波段, 提取结果对PLSR、 SVR、 MLR三种模型精度提升明显, 而SPA算法对ANN模型提升效果较好。 在本研究中, CARS算法选择的波段建模精度最优, 选择的波段主要集中在400~500、 800~1 000、 1 300~1 700以及2 100~2 450 nm之间。

(3)经过SG+SNV+SD处理后, 线性模型CARS+PLS和CARS+MLR两种组合的反演精度近似, 均优于UVE+PLS和UVE+MLR组合。 非线性模型的反演精度排序: CARS+SVR> UVE+SVR> SPA+ANN。 其中CARS+PLS模型效果最好, R2为0.97, RMSE为5.25 mg· kg-1, MAE为4.35 mg· kg-1, RPD为3.94, 模型效果最好。 由于本研究样本量较小, 神经网络的训练结果较差, 线性模型PLSR预测能力优于非线性模型ANN, 而对于SVR模型在小样本较高特征维度数据的表现非常优秀。

本研究表明, 通过不同特征波段选择方法和反演模型的组合, 来提高模型系统对土壤重金属污染浓度的反演的精度具有可行性。 在后续研究中可引入其他优化算法和建模方式对各类模型进行验证, 同时增加多种样本以探究模型泛化的可能。 此外, 本研究使用的土壤为农田土壤, 样本含有多种元素和重金属, 研究得到的光谱反射率是多种元素共同响应的结果, 如果能采用控制实验, 找到对Cr含量具有敏感响应的特征波段, 可能会对其含量反演精度的提高更有帮助。

参考文献
[1] WANG Yue, LIU Ying-xue, LI Dan-dan, et al(王玥, 刘莹雪, 李丹丹, 等). Journal of Agro-Environment Science(农业环境科学学报), 2021, 40(12): 2723. [本文引用:1]
[2] Ding S, Zhang X, Sun W, et al. Journal of Soils and Sediments, 2022, 22(5): 1431. [本文引用:2]
[3] Zhang J, Wang M, Yang K, et al. International Journal of Environmental Research and Public Health, 2022, 19(13): 7755. [本文引用:1]
[4] Wu T, Yu J, Lu J, et al. Agriculture, 2020, 10(7): 292. [本文引用:1]
[5] Hou L, Li X, Li F. Journal of Environmental Quality, 2019, 48(1): 57. [本文引用:2]
[6] Trifi M, Gasmi A, Carbone C, et al. Environmental Science and Pollution Research, 2022, 29(58): 87490. [本文引用:2]
[7] Ahmad S, Pand ey A C, Kumar A, et al. Applied Geomatics, 2021, 13: 361. [本文引用:1]
[8] ZHANG Xia, SUN You-xin, SHANG Kun, et al(张霞, 孙友鑫, 尚坤, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2024, 55(1): 186. [本文引用:1]
[9] TU Yu-long, ZOU Bin, JIANG Xiao-lu, et al(涂宇龙, 邹滨, 姜晓璐, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2018, 38(2): 575. [本文引用:1]
[10] AN Bai-song, WANG Xue-mei, HUANG Xiao-yu, et al(安柏耸, 王雪梅, 黄晓宇, 等). Earth and Environment(地球与环境), 2023, 51(2): 246. [本文引用:1]
[11] Zhao L, Hu Y M, Zhou W, et al. Sustainability, 2018, 10(7): 2474. [本文引用:1]
[12] GAO Zhong-yuan, XIAO Rong-bo, WANG Peng, et al(高中原, 肖荣波, 王鹏, 等). Environmental Science(环境科学), 2021, 42(1): 343. [本文引用:1]
[13] Guo H, Yang K, Wu F, et al. Sensors, 2023, 23(21): 8756. [本文引用:2]
[14] MENG Shan, LI Xin-guo, JIAO Li (孟珊, 李新国, 焦黎). Chinese Journal of Soil Science, 2023, 54(2): 286. [本文引用:1]
[15] Akbari D. IET Image Processing, 2019, 13(12): 2169. [本文引用:1]
[16] Su L, Shi W, Chen X, et al. Food Chemistry, 2021, 338: 127797. [本文引用:1]
[17] Sekulic Z, Antanasijevic D, Stevanovic S, et al. International Journal of Environmental Science and Technology, 2017, 14(7): 1383. [本文引用:1]
[18] CHEN Jun-jian, ZHANG Hui-hua, LIU Jian-ming, et al(陈俊坚, 张会化, 刘鉴明, 等). Ecology and Environmental Sciences(生态环境学报), 2011, 20(4): 646. [本文引用:1]
[19] CHENG Yong-sheng, ZHOU Yao (成永生, 周瑶). The Chinese Journal of Nonferrous Metals(中国有色金属学报), 2021, 31(11): 3450. [本文引用:1]