引用本文
钟晴, 麦麦提吐尔逊#cod#x000b7;艾则孜, 米热古力#cod#x000b7;艾尼瓦尔, 侯茂蕤, 李浩然. 城市土壤钴含量高光谱反演[J]. 光谱学与光谱分析, 2024,44(11): 3266-3272.
ZHONG Qing, Mamattursun EZIZ, Mireguli AINIWAER, HOU Mao-rui, LI Hao-ran. Hyperspectral Inversion of Cobalt Content in Urban Soils[J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3266-3272.
Doi:10.3964/j.issn.1000-0593(2024)11-3266-07  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
城市土壤钴含量高光谱反演
钟晴1, 麦麦提吐尔逊·艾则孜1,2,*, 米热古力·艾尼瓦尔1,2, 侯茂蕤3, 李浩然4
1.新疆师范大学地理科学与旅游学院, 新疆 乌鲁木齐 830054
2.新疆干旱区湖泊环境与资源实验室, 新疆 乌鲁木齐 830054
3.天津工业大学计算机科学与技术学院, 天津 300380
4.陕西师范大学地理科学与旅游学院, 陕西 西安 710119
*通讯作者 e-mail: oasiseco@126.com

作者简介: 钟 晴, 1998年生, 新疆师范大学地理科学与旅游学院硕士研究生 e-mail: 13235366308@163.com

收稿日期: 2023-07-19 修回日期: 2024-01-16
基金: 国家自然科学基金项目(U2003301)资助
摘要

钴元素(Co)被国际癌症研究机构(IARC)列为2B类致癌物, 对城市生态系统的安全有潜在危害, 如何快速、 准确检测土壤中Co元素含量尤为重要。 高光谱技术对土壤Co含量反演具有极大潜力。 在新疆乌鲁木齐市采集表层(0~20 cm)土壤样品88个, 测定Co含量和原始光谱反射率, 对原始光谱反射率进行预处理和均方根(RMS)、 对数(LT)、 对数的倒数(RL)、 倒数(RT)、 倒数的对数(AT)、 一阶微分(FD)、 二阶微分(SD)、 倒数一阶微分(RTFD)、 倒数二阶微分(RTSD)、 对数一阶微分(LTFD)、 对数二阶微分(LTSD)、 均方根一阶微分(RMSFD)、 均方根二阶微分(RMSSD)、 倒数的对数一阶微分(ATFD)、 倒数的对数二阶微分(ATSD)、 对数的倒数一阶微分(RLFD)和对数的倒数二阶微分(RLSD)等17种变换。 将18种形式的土壤反射率光谱值与Co含量进行Pearson相关性分析(PCC)和CARS优化, 筛选出用于建模的特征光谱变量。 将筛选出的光谱特征变量分别作为自变量, 土壤Co含量作为因变量, 基于偏最小二乘回归(PLSR)、 随机森林回归(RFR)和支持向量机回归(SVMR)三种算法, 构建城市土壤Co含量高光谱反演模型, 模型的评价指标采用决定系数( R2)、 均方根误差(RMSE)和平均绝对误差(MAE)。 结果表明: 城市土壤Co含量的高光谱模型的稳定性和估算精度由高到低依次为RFR模型、 PLSR模型、 SVMR模型。 Co含量的最佳估算模型是ATFD-RFR模型( R2=0.871, RMSE=0.124, MAE=0.273), 相较R-RFR模型 R2提高了0.335, RMSE减少了0.32, MAE减少了0.243, RPD为7.90。 光谱变换可以有效增强光谱特征, 一阶微分变换对光谱特征的增强效果最显著, 其中, RTFD不仅可以有效增强Co的光谱特征, 还可以很好地提高模型的估算精度。 在样点空间异质性不显著、 实测值低且均匀时, RFR模型可以在绿洲城市土壤高光谱反演估算中推广。

关键词: 高光谱; 钴(Co)元素; 反演模型; 乌鲁木齐; 城市土壤
中图分类号:TP79 文献标志码:A
Hyperspectral Inversion of Cobalt Content in Urban Soils
ZHONG Qing1, Mamattursun EZIZ1,2,*, Mireguli AINIWAER1,2, HOU Mao-rui3, LI Hao-ran4
1. College of Geographical Science and Tourism, Xinjiang Normal University, Urumqi 830054, China
2. Laboratory of Arid Zone Lake Environment and Resources, Xinjiang Normal University, Urumqi 830054, China
3. College of Computer Science and Technology, Tiangong University, Tianjin 300380, China
4. School of Geography and Tourism, Shaanxi Normal University, Xi'an 710119, China
*Corresponding author
Abstract

Cobalt (Co) was classified as a group 2B carcinogen by the International Agency for Research on Cancer. It is potentially harmful to the safety of the entire urban ecosystem, and it is particularly important to quickly and accurately detect soil Co content. Hyperspectral techniques have great potential for inversion of soil Co content. 88 surface (0~20 cm) soil samples were collected from Urumqi, Xinjiang, to determine the Co content and original spectral reflectance. The original spectral reflectance was preprocessed and applied with 17 types of transformation, which include the root-mean-square (RMS), the logarithm of the logarithm (LT), the inverse of the logarithm (RL), the inverse of the logarithm (RT), the logarithm of the inverse (AT), the first-order differentiation (FD), the second-order differentiation (SD), the inverse first-order differentiation (RTFD) (RTSD), logarithmic first-order differentiation (LTFD), logarithmic second-order differentiation (LTSD), root-mean-square first-order differentiation (RMSFD), root-mean-square second-order differentiation (RMSSD), logarithmic first-order differentiation of the inverse (ATFD), logarithmic second-order differentiation of the inverse (ATSD), logarithmic first-order differentiation of the inverse (RLFD) and logarithmic second-order differentiation ( RLSD). Then, the Co content and 18 types of soil spectral data were subjected to Pearson correlation analysis (PCC) and CARS to screen the spectral signature variables for modeling. The soil Co content was taken as the dependent variable, and the screened spectral feature variables were taken as independent variables. Based on three algorithms, namely partial least squares regression (PLSR), random forest regression (RFR), and support vector machine regression (SVMR), the hyperspectral inversion models of urban soil Co content were constructed, and the coefficient of determination ( R2), the root-mean-square error (RMSE) and the mean absolute error (MAE) were used as the evaluation indexes. Some conclusions can be drawn: The hyperspectral models' estimation accuracy and stability for urban soil's Co content are in descending order of the RFR, PLSR, and SVMR models. The best estimation model for Co content is the ATFD-RFR model ( R2=0.871, RMSE=0.124, MAE=0.273) which the RPD is 7.90; in this model, compared with the R-RFR model, the R2 improved from 0.536 to 0.871, RMSE and MAE reduced by 0.32 and 0.243, respectively. Spectral transform can effectively enhance the spectral features; enhancement of spectral features is most significant with first-order differential transform, among which the RTFD can not only effectively enhance the spectral features of Co but also improve the estimation accuracy of the model very well. The RFR model can be extended in oasis urban soil hyperspectral inversion estimation when the spatial heterogeneity of sample sites is insignificant, and the measured values are low and homogeneous.

Keyword: Hyperspectral; Cobalt element (Co); Inversion model; Urumqi city; Urban soil
引言

城市土壤在城市生态系统中起着关键作用。 钴元素(Co)作为被国际癌症研究机构(IARC)列出的2B类致癌物[1], 对整个城市生态系统的安全有潜在危害。 Co是人体必需的微量元素, 刺激人体造血功能, 参与辅酶反应, 几乎分布于各个器官和细胞, 常用于医疗研究; 但长期暴露于Co过量的环境中可引起Co中毒, 造成严重的金属沉着病, 损害呼吸系统, 循环系统, 内分泌系统和神经系统, 降低机体抵抗力[2, 3]。 有学者对土壤的重金属含量进行分析, 证实Co是危险性最高的非致癌健康风险因子[4, 5], 也有相关研究证明河南桐柏和沁阳地区[6]、 黄河中段河流阶地[7]和北京市的土壤Co含量超过相关土壤背景值, 污染严重, 对成人和儿童的健康均有不同程度的影响。 Alexakis[8]发现希腊农业生产区土壤中Co富集明显, 存在潜在的健康风险和生态风险。 Sukalic等[9]在黑塞哥维纳采集了三个农业区的土壤样品, 对其进行Co含量分析及人类健康风险评估, 最终证实Co含量超过所有土壤类型所允许的最大浓度, 对成人和儿童都有潜在的致癌风险。 因此, 开展对土壤Co含量的检测研究具有重大意义。

土壤中Co的有3种存在形式, 分别为独立Co矿物、 呈类质同象或包裹体存在于某一矿物中的Co以及呈吸附形式存在于某些矿物表面的Co, 其中第2种存在形式最为普遍。 传统的Co含量测定方法虽然精度高, 但操作复杂、 耗时耗力、 价格昂贵, 所用试剂可能对环境产生二次污染[10]。 高光谱遥感技术能根据光谱特征对地物进行识别和反演, 操作简单、 效率高、 成本低, 并能快速无损地进行大规模的实时动态监测, 是一种快速获取土壤重金属元素信息的新方法[10, 11, 12]。 土壤重金属高光谱反演研究的关键是对土壤重金属的光谱特征进行处理和分析, 筛选出土壤重金属响应的特征波段, 进而构建高光谱模型对土壤重金属含量进行反演预测[13]。 近年来, 偏最小二乘回归(PLSR)[14]、 随机森林回归(RFR)[15]、 支持向量机回归(SVMR)[16]和BP神经网络(BPNN)[17]等模型被广泛应用于估算土壤重金属含量, 效果显著, 但是有关土壤Co含量的高光谱反演研究太少, 仅季建万等[10]运用UR、 MSR和PLSR模型对莆田市木兰溪下游两岸的城市土壤Co含量进行了高光谱反演研究, 并验证了PLSR模型为最佳估算模型(R2=0.681, RMSE=1.483, RPD=1.665)。

基于此, 以新疆乌鲁木齐市为研究区域, 以土壤钴(Co)含量为研究对象, 构建PLSR、 RFR和SVMR三种高光谱模型, 分析三种模型在城市土壤Co含量高光谱反演研究中的适应性以及局限性, 为实现绿洲城市土壤Co含量的快速监测提供理论和技术支持。

1 实验部分
1.1 研究区概况

研究区(86° 37'33″— 88° 58'24″E, 42° 45'32″— 44° 08'00″N)位于中国西北干旱区典型的绿洲城市— 新疆乌鲁木齐市, 地处亚欧大陆腹地, 温带大陆性气候特征明显, 多年平均气温6.7 ℃, 多年平均降水量为280 mm, 多年平均蒸发量为2 730 mm。 乌鲁木齐市三面环山, 地形起伏大, 地势东南高, 西北低, 北部为河流冲积平原, 地形较开阔, 土壤类型主要以灰漠土为主。 作为新疆首府和丝绸之路经济带上的核心城市, 乌鲁木齐市城市化速度快, 人口密度大, 工业发展较为先进, 生产生活排放导致土壤重金属污染问题日益突出。

1.2 土样采集与测定

在研究区范围内采集88个表层(0~20 cm)土壤样品(图1)。 每个土壤样品均由5个子样混合而成, 重500 g以上。 所有样品室内自然风干, 剔除杂物, 混匀研磨后分成两份, 分别用于重金属元素含量测定和光谱测定。 采用电感耦合等离子质谱仪(ICP-MS 7800)进行土壤Co全量的测定, 检测依据均为《HJ 803— 2016》[18], Co的测试回收率介于94.34%~106.12%, 在允许范围内。

图1 研究区位置及采样点分布图Fig.1 Location of the study area and sampling sites

1.3 光谱数据测定与处理

采用美国ASD公司生产的便携式地物光谱仪FieldSpe c3, 在室外干扰因素少的区域测定土样光谱数据, 波段范围为350~2 500 nm。 测定光谱数据时, 先预热仪器, 将40 cm× 40 cm的白板置于2 m× 2 m的黑色卡纸上进行定标, 获取绝对反射率, 然后使土样在黑色卡纸上保持自然状态, 并将传感器探头垂直放于土样表面上方15 cm处, 传感器探头每隔5 min用白板优化一次。 每个土样测定15次光谱曲线, 去除噪声较大的异常波段后, 保留400~1 349、 1 431~1 780和1 971~2 400 nm共1 730个波段用于后续建模。 利用ViewSpecPro软件对15条光谱曲线进行均值化处理, 将其算术平均值作为土样原始光谱反射率。 采用Savitzky-Golay法对土样原始光谱反射率进行处理, 去除“ 毛刺” 噪声。 不同土样的光谱曲线如图2所示。

图2 原始(a)和Savitzky-Golay平滑处理(b)后的光谱反射率曲线Fig.2 Original (a) and Savitzky-Golay smoothing (b) reflectance spectra

1.4 光谱变换与特征波段选取

高维和高冗余的土壤光谱会影响模型反演的精度和稳定性[15]。 因此, 对土壤原始光谱数据(R)进行均方根(RMS)、 对数(LT)、 对数的倒数(RL)、 倒数(RT)、 倒数的对数(AT)、 一阶微分(FD)、 二阶微分(SD)、 倒数一阶微分(RTFD)、 倒数二阶微分(RTSD)、 对数一阶微分(LTFD)、 对数二阶微分(LTSD)、 均方根一阶微分(RMSFD)、 均方根二阶微分(RMSSD)、 倒数的对数一阶微分(ATFD)、 倒数的对数二阶微分(ATSD)、 对数的倒数一阶微分(RLFD)和对数的倒数二阶微分(RLSD)等17种光谱变换。 其次, 将土壤Co含量与18种形式的土壤光谱数据进行Pearson相关性分析(PCC)和CARS优化, 筛选出用于建模的光谱特征变量。 将土壤Co含量作为因变量, 不同变换形式的光谱特征变量分别作为自变量, 进行高光谱模型的反演。 平滑处理、 光谱变换及相关性分析均在Matlab(R2019b)软件中完成。

1.5 模型建立与检验

Co含量的高光谱反演估算模型选用随机森林回归(RFR)、 偏最小二乘回归(PLSR)和支持向量机回归(SVMR)三种回归方法构建。 模型的构建在Python中完成。 随机森林回归模型(RFR)作为利用多棵决策树对样本进行训练并估算的机器学习算法, 集合众多决策树, 采用Bootsrap重抽样方法随机抽样构建不同的分类模型并组成多分类模型系统, 泛化能力强, 模型鲁棒性高[19]。 偏最小二乘回归模型(PLSR)是构建高光谱模型的基本、 通用方法[20]。 SVMR模型是非线性预测模型, 利用特定的传递核函数将样本矩阵映射到高维特征空间, 以区间最大化分割原则对不同样本进行分割, 进而对土壤重金属含量进行反演预测[17]。

选取决定系数(R2)、 均方根误差(RMSE)和平均绝对误差(MAE)对模型进行评估, R2为负值, 说明模型的估算能力不好, R2为正值, 且越趋近于1, 则模型的拟合程度越好, 稳定性越高, RMSE和MAE的值越小, 则模型估算精度和鲁棒性越高。

2 结果与讨论
2.1 土壤Co含量统计

表1为乌鲁木齐市土壤样品实测的Co含量统计。 从Co的含量看, Co的均值与最大值均未超过乌鲁木齐市土壤背景值[21], 说明研究区受Co的影响不大。 从空间分布来看, Co的变异系数低于20%, 说明Co在土壤中的空间异质性不显著。 为保证建模样本与验证样本划分的合理性, 利用计算机算法将样本随机划分为70个(80%)建模样本和18个(20%)验证样本。 表1可见, 建模样本与验证样本的均值、 标准差和变异系数基本一致, 划分较为合理, 可以用于后续建模。

表1 乌鲁木齐市Co含量描述性统计特征 Table 1 Descriptive statistical characteristics of Co content in Urumqi City
2.2 土壤Co含量与光谱变量的相关分析

土壤光谱反射率测定中存在随机误差, 且Co元素在土壤中含量较低, 其光谱响应信号微弱, 采用土壤原始光谱数据直接反映特征波段较难, 需根据Co元素的光谱吸收特征筛选特征波段。 将18种形式的土壤光谱值与土壤Co含量进行Pearson相关性分析(PCC), 筛选出相关系数绝对值在0.01水平上显著相关的特征光谱变量, 部分转换后的光谱数据其相关系数绝对值低于0.01水平上的临界值, 便统一使用1 730个光谱波段的光谱数据进行建模(表2)。 从表2可以看出: 原始光谱数据(R)及五种数学变换后的光谱数据(AT、 RMS、 LT、 RL、 RT)与土壤Co含量在p< 0.01水平上显著不相关, 其他变换形式的光谱数据与土壤Co含量均达到0.01的极显著性水平, 不同光谱变换对Co的光谱特征有着不同的增强效果, 一阶微分提取的光谱特征变量多于二阶微分。 其中, RTFD对Co光谱特征的增强效果最显著, 表现为该变换形式的光谱数据与土壤Co含量进行Pearson相关分析后筛选出的特征波段数量最多。

表2 不同光谱变换的特征波段数量统计 Table 2 Statistics of the number of characteristic bands selected from the spectra processed by different spectral transformations

基于Python, 构建CARS优化算法, 选取10次迭代次数高于25次所筛选出的波段, 并进行统计分析, 最终选择出现频次高于6次的波段作为光谱特征变量用于高光谱反演建模。 CARS筛选出的特征光谱变量的数量明显少于Pearson相关性分析筛选出的特征光谱变量, 且数量分布均匀。

2.3 土壤Co含量估算模型的对比分析

Pearson相关性分析(PCC)筛选的特征光谱变量和CARS优化光谱数据提取的特征光谱变量分别作为自变量, 土壤Co含量作为因变量, 利用PLSR、 RFR和SVMR模型对土壤Co含量进行回归分析, 并采用决定系数(R2)、 均方根误差(RMSE)和平均绝对误差(MAE)作为评价指标。

不同的高光谱反演模型对土壤Co含量的反演估算精度是不同的。 如图3所示, Pearson相关性分析筛选出的特征光谱变量建模效果总体优于CARS优化光谱数据提取的特征光谱变量, RFR模型的稳定性和精度优于PLSR模型和SVMR模型。 从Pearson相关性分析(PCC)筛选的特征光谱变量来看, 在RFR模型中, 基于一阶微分变换和二阶微分变换的RFR模型估算精度均显著提高, 其余变换形式的RFR模型估算精度低于R-RFR。 在PLSR模型中, 除了RL-PLSR外, 其余变换形式的PLSR模型的估算精度均提高(一阶微分> 二阶微分> 微分)。 在SVMR模型中, 基于一阶微分和二阶微纷变换的SVMR模型的估算精度总体优于R-SVMR模型, 一阶微分变换的SVMR模型的稳定性较强, 基于微分变换的SVMR模型估算的R2比R-SVMR模型略有降低。 从CARS优化光谱数据提取的特征光谱变量来看, 在RFR模型中, 基于微分变换的RFR模型估算精度降低, 基于其余变换形式的光谱变量构建的RFR模型的估算能力均提高。 PLSR模型估算精度的波动范围较大, 基于CARS-AT、 CARS-LTFD、 CARS-RTFD、 CARS-RTSD、 CARS-ATSD和CARS-FD的PLSR模型的估算精度比CARS-R-PLSR模型低, 基于其余变换形式的光谱变量的PLSR模型估算效果均显著提高。 在SVMR模型中, 基于微分变换的光谱变量的SVMR模型估算的R2略有降低, 基于一阶微分变换和二阶微分变换的SVMR模型的估算精度均较R-SVMR有了不同程度的提高。

图3 乌鲁木齐市土壤Co含量反演模型精度统计Fig.3 Accuracy statistics of the inversion model of soil Co content in Urumqi city

2.4 土壤Co含量预测模型的最优组合及讨论

由于RFR模型具有随机性, 决策树的数量会干扰模型的估算性能, 在考虑模型性能、 模型运行时间和样本数量等因素后, 分别将RFR模型的三个参数(random_state1、 n_estimators和random_state2)分别设置为19, 6和48。 Co含量高光谱估算模型的最优组合为ATFD-RFR模型(R2=0.871, RMSE=0.124, MAE=0.273), 估算模型的RPD为7.90, 模型的估算能力好, 估算精度高于文献[11]。 这表明非线性模型对土壤中Co含量可能具有更好的估算能力。 在Co含量的高光谱估算中, 用筛选出的各变换的光谱特征变量参与建模的效果比用原始光谱数据进行建模的效果好, 一阶微分变换在建模中的作用最为突出。 说明一阶微分变换不仅能有效增强光谱特征, 还可以很好地提高模型估算精度。

模型的验证效果也进一步证实了以上结果, 利用变换后的光谱特征变量建模计算出的预测值和实测值回归的决定系数R2较原始光谱数据建模显著提高, 且RMSE和MAE均有明显的降低。 图4为验证样本的Co含量实测值与预测值的散点图, 可以直观地看出, 基于原始数据建立的RFR高光谱预测模型效果不理想, Co含量实测值和预测值之间的决定系数R2为0.536, 基于光谱变换后筛选出的特征变量建立的高光谱模型预测精度提高显著, 实测值和预测值之间存在很好的吻合度, 决定系数分别为0.871, 较R-RFR模型提高了0.335。

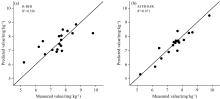图4 乌鲁木齐市土壤Co含量最优预测模型实测值与预测值散点图Fig.4 Scatter plots of measured and predicted values of the optimal prediction model for soil Co content in Urumqi

不论是用原始光谱数据建模还是用变换后的特征光谱变量进行建模, 实测值偏低时, 其预测值略微偏高, 实测值接近验证样本点的均值时, 预测值和实测值之间的吻合度较好, 实测值偏高时, 预测效果降低, 说明误差可能受到土壤Co含量实测值波动范围的影响。 由于样点有限, 且样点的Co含量分布较为均匀, 是否存在实测值均匀的样本点预测效果较好, 实测值高和实测值低的样本点预测效果差的问题还有待验证。 其次, 近年来分数阶微分在土壤光谱学领域应用取得良好成效[22], 而本研究使用的是整数阶光谱微分, 分数阶光谱微分是否更加适合本研究区有待探究。

构建的RFR模型可用于含量分布较为均匀的区域的土壤重金属估算, 可以在绿洲城市土壤重金属反演研究中进行推广, 在今后研究中, 应适当增加采样点数量, 丰富实测值较低和较高的样点数。 在对模型进行优化的同时更要探究其他的光谱处理方法, 改善模型的估算精度及适应性, 验证模型是否适用于未受污染区和重度污染区的土壤重金属高光谱估算, 以期能更高精度的对大范围区域的土壤重金属含量进行实时动态监测。

3 结论

通过对比分析偏最小二乘回归(RLSR)、 随机森林回归(RFR)和支持向量机回归(SVMR)三种模型对城市土壤Co含量估算能力, 得出以下结论:

(1)城市土壤Co含量的高光谱模型的稳定性和估算精度从大到小依次为RFR模型、 PLSR模型和SVMR模型。 最优估算模型是ATFD-RFR模型(R2=0.871, RMSE=0.124, MAE=0.273), 与R-RFR模型相比, R2提高了0.335, RMSE减少了0.32, MAE减少了0.243, RPD为7.90。

(2)土壤中Co元素含量较低, 光谱信息微弱, 利用原始光谱数据进行建模估算的效果较差, 光谱变换可以有效增强光谱特征, RTFD对光谱特征的增强效果最显著, RTFD和ATFD的建模效果最好。 其中, RTFD不仅能有效增强Co在土壤中的光谱特征, 而且该变换的光谱值在部分估算土壤Co含量的高光谱模型中均有较好的表现, 能够较好地提高估算效果。 ATFD虽然没能很好地突出土壤中Co的光谱信息, 但是却能较好的提高模型估算精度。

(3)在今后的研究中, 应当丰富实测值较低和较高的样点数, 验证模型是否适用于未受污染区和重度污染区的土壤重金属高光谱估算。 其次, 应当探究更多的处理方法, 并不断优化模型, 使其能更高精度的对大范围区域的土壤重金属含量进行实时动态监测, 为土壤重金属的高光谱研究提供理论和技术支持。

参考文献
[1] International Agency for Research on Cancer, World Health Organization. Group Ⅱ Carcinogen List. 2017. www.nmpa.gov.cn. [本文引用:1]
[2] LIU Wu-zhong, WANG Jian-ming, ZHANG Hong, et al(刘武忠, 王剑明, 张红, 等). Occupational Health and Emergency Rescue(职业卫生与应急救援), 2016, 34(2): 111. [本文引用:1]
[3] LI Peng, DING Da-lian, ZENG Xiang-li, et al(李鹏, 丁大连, 曾祥丽, 等). Chinese Journal of Otology(中华耳科学杂志), 2015, 13(1): 57. [本文引用:1]
[4] Wu Y H, Liu Q Y, Ma J, et al. Environmental Pollution, 2022, 293: 118554. [本文引用:1]
[5] Sharma S, Nagpal A K, Kaur I. Food Chemistry, 2018, 255(30): 15. [本文引用:1]
[6] LAI Shu-ya, DONG Qiu-yao, SONG Chao, et al(赖书雅, 董秋瑶, 宋超, 等). Geology in China(中国地质), 2023, 50(1): 222. [本文引用:1]
[7] DAI Yan-yan, CHAO Jin-long, CAI Xin, et al(戴燕燕, 钞锦龙, 蔡昕). Jouranl of Taiyuan Normal University (Natural Science Edition)[太原师范学院(自然科学版)], 2020, 19(2): 78. [本文引用:1]
[8] Alexakis D. Archives of Agronomy and Soil Science, 2016, 62(3): 359. [本文引用:1]
[9] Sukalic A, Ahmetovic N, Mackic S, et al. ACS Agriculturae Conspectus Scientificus, 2017, 83(1): 45. [本文引用:1]
[10] JI Jian-wan, ZHANG Rui, SHA Jin-ming, et al(季建万, 张锐, 沙晋明). Journal of Fujian Normal University (Natural Science Edition)[福建师范大学学报(自然科学版)], 2019, 35(5): 23. [本文引用:3]
[11] Sawat R, Rasim N, Abliz A, et al. International Journal of Applied Earth Observation and Geoinformation, 2018, 73: 14. [本文引用:2]
[12] YUAN Zi-ran, WEI Li-fei, ZHANG Yang-xi, et al(袁自然, 魏立飞, 张杨熙, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(2): 567. [本文引用:1]
[13] JIANG Zhen-lan, YANG Yu-sheng, SHA Jin-ming (江振蓝, 杨玉盛, 沙晋明). Acta Geographica Sinica(地理学报), 2017, 72(3): 533. [本文引用:1]
[14] Choe E, van der Meer P, van Ruitenbeek P, et al. Remote Sensing of Environment, 2008, 112: 3222. [本文引用:1]
[15] Wei L F, Yuan Z R, Zhong Y F, et al. Applied Sciences, 2019, 9: 1943. [本文引用:2]
[16] Lin N, Jiang R Z, Li G J, et al. Ecological Indicators, 2022, 143: 109330. [本文引用:1]
[17] Han L, Chen R, Zhu H L, et al. Sustainability, 2020, 12: 1476. [本文引用:2]
[18] Ministry of Environmental Protection of the People's Republic of China(中华人民共和国环境保护部). HJ803-2016 Soil and Sediment—Determination of Aqua Regia Extracts of 12 Metal Elements—Inductivity Coupled Plasma Mass Spectrometry(HJ803-2016 土壤和沉积物 12种金属元素的测定王水提取-电感耦合等离子体质谱法). Beijing: China Environmental Science Press(北京: 中国环境科学出版社), 2016. [本文引用:1]
[19] Liu W W, Li M J, Zhang M Y, et al. Environmental Science and Pollution Research, 2020, 27: 22935. [本文引用:1]
[20] Wei L F, Pu H C, Wang Z X, et al. Sensors, 2020, 20: 4056. [本文引用:1]
[21] HAYRAT Adila, EZIZ Mamattursun, JIN Wan-gui, et al(阿地拉·艾来提, 麦麦提吐尔逊·艾则孜, 靳万贵, 等). Geology in China(中国地质), 2020, 47(6): 1915. [本文引用:1]
[22] Hong Y S, Liu Y L, Chen Y Y, et al. Geoderma, 2019, 337: 758. [本文引用:1]