引用本文
邓志刚, 赵红梅, 查文娴, 汤林玲, 田野. 基于量子遗传光谱角分类算法的高光谱植被特征波段选取[J]. 光谱学与光谱分析, 2024,44(11): 3258-3265.
DENG Zhi-gang, ZHAO Hong-mei, ZHA Wen-xian, TANG Lin-ling, TIAN Ye. A Hyperspectral Vegetation Feature Band Selection Based on Quantum Genetic Spectral Angle Mapper Algorithm[J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3258-3265.
Doi:10.3964/j.issn.1000-0593(2024)11-3258-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于量子遗传光谱角分类算法的高光谱植被特征波段选取
邓志刚1,2, 赵红梅2,*, 查文娴2, 汤林玲2, 田野2
1.华东交通大学信息与软件工程学院, 江西 南昌 330013
2.江西师范大学鄱阳湖湿地与流域研究教育部重点实验室/地理与环境学院, 江西 南昌 330022
*通讯作者 e-mail: zhm8012@jxnu.edu.cn

作者简介: 邓志刚, 1976年生, 华东交通大学信息与软件工程学院讲师 e-mail: dzgstudy@163.com

收稿日期: 2024-02-24 修回日期: 2024-05-22
基金: 国家自然科学基金项目(42161062, 42361066), 鄱阳湖湿地与流域研究教育部重点实验室开放基金项目(PK2020001)资助
摘要

高光谱数据往往具有数百个连续的窄波段, 能够反应地物必要且详细的光谱反射信息, 因而被广泛应用于地物精细分类中。 然而, 由于高光谱窄波段间较强的相关性和冗余性, 将整个原始高光谱数据应用于实际分类中, 并不能获得令人满意的精度。 因此, 特征波长或波段选择一直以来都是高光谱实际应用的关键和难点所在。 前期的特征波段选择方法不仅计算效率低, 容易陷于局部优化, 而且波段指向性和解释性不强。 以鄱阳湖湿地连续极端干旱情况下1月—5月份枯水期植被物种精细分类中的特征波段选择为例, 采用便携式地物光谱仪(SVC HR1024)实测的包括青蓼、 藜蒿、 紫云英、 风花菜、 长刺酸模、 看麦娘、 虉草、 苔草、 南荻、 芦苇等10种湿地植物物种的高光谱反射数据, 引入量子遗传算法(QGA), 综合基于k近邻分类器的光谱角分类方法(KNN-SAM), 提出基于量子遗传k近邻光谱角分类算法(QGA-KNN-SAM), 获取适用于湿地植被高光谱精细分类的特征波长, 同时采用k中心点聚类算法确定特征波段区间。 该算法与基于传统遗传k近邻光谱角分类算法(GA-KNN-SAM)进行对比实验发现, QGA-KNN-SAM的平均分类精度为95%左右, 明显高于GA-KNN-SAM的平均分类精度90%; 且基于QGA-KNN-SAM算法的特征波长点及波段相对聚焦, 其跨度为589~634.4 nm, 明显低于GA-KNN-SAM的1 107.6~1 205 nm。 与传统植被的精细分类不同, 湿地植被的精细分类除考虑反应植被的光谱波段外, 还需要考虑反应地表水文特征的波段信息。 与目前常见的多光谱及高光谱卫星影像的波段分布对比发现, QGA-KNN-SAM算法选取的特征波段的指向性和可解释性更优。 该算法既提高了波段选择的计算效率和可解释性, 又弥补了在波段选择研究中QGA方法的缺失, 可为同类研究提供科学支撑。

关键词: 量子遗传算法; 光谱角绘图; 湿地植被; 高光谱波段选择
中图分类号:TP751.1 文献标志码:A
A Hyperspectral Vegetation Feature Band Selection Based on Quantum Genetic Spectral Angle Mapper Algorithm
DENG Zhi-gang1,2, ZHAO Hong-mei2,*, ZHA Wen-xian2, TANG Lin-ling2, TIAN Ye2
1. School of Information and Software Engineering, East China Jiaotong University, Nanchang 330013, China
2. Key Laboratory of Poyang Lake Wetland and Watershed Research (Jiangxi Normal University), Ministry of Education, Nanchang 330022, China
*Corresponding author
Abstract

Hyperspectral data collects essential and detailed spectral responses from ground objects through hundreds of contiguous narrow spectral wavelength bands and is widely used for vegetation fine classification. However, classification accuracy is not often satisfactory in a cost-effective way when using all original hyperspectral information (HSI) for practical applications because of its strong correlation and redundantness. Therefore, feature wavelength/band selection is crucial and difficult for HSI applications. Previous band selection methods have some drawbacks, such as low computation efficiency, lack of interpretability, being trapped in local optimization, and so on. Our study focuses on the hyperspectral feature band selection for the vegetation species fine classification of Poyang Lake wetland in continuous extreme drought conditions. Hyperspectral reflectance data of 10 plant species, such as Green polygonum, Artemisia Selengensis, Astragalus sinicus, Rorippa globose, Rumex trisetifer Stokes, Sonoma alopecurus, Phalaris arundinacea, Carexcinerascens, Miscanthus sacchariflorus and Phragmites australis collected by SVC spectrometer (SVC HR1024) is used in this work. We introduce the Quantum Genetic Algorithm (QGA), which is combined with Spectral Angle Mapper-based k-Nearest Neighbors classifier (KNN-SAM), and propose a new feature band selection algorithm, i.e., QGA-KNN-SAM, to select feature wavelength. Then, we use the K-Medoide clustering algorithm to determine the feature band interval. In our experiment, the classification performance of the proposed QGA-KNN-SAM is compared with the traditional GA-KNN-SAM algorithm. QGA-KNN-SAM generates an average classification accuracy value of 95%, higher than GA-KNN-SAM (90%). Moreover, QGA-KNN-SAM generates the feature bands range between 589~634.4 nm, which is relatively more concentrated than achieved by GA-KNN-SAM (1 107.6~1 205 nm). A wavelength band that reflects the surface hydrological characteristics and vegetation should be considered in the fine classification of wetland vegetation, which is different from the fine classification of traditional vegetation. Compared with the band distribution of commonly used multispectral and hyperspectral satellite images, it is found that the QGA-KNN-SAM algorithm selects feature bands with better directionality and interpretability. This algorithm improves the computational efficiency and interpretability of band selection and compensates for the lack of the QGA method in band selection research, providing methodological and theoretical support for similar studies.

Keyword: Quantum genetic algorithm (QGA); Spectral angle mapper (SAM); Wetland vegetation; Hyperspetral band selection
引言

高光谱数据可敏感地获取不同植物物种光谱反射率的微小差异[1], 为植被精细分类提供了可能[2, 3]。 然而, 高光谱数据处理中存在的多共线性特征, 使得高光谱数据冗余度较高。 伴随高光谱植被精细分类的发展, 特征波段的选择成为高光谱数据深入应用中不可逾越的重点和难点所在。

传统的特征提取和波段选择的方法以秩统计和聚类方法为主。 秩统计方法包括不考虑波段间的相关性的信息熵和去噪误差匹配算法[4], 考虑波段相关性的互信息[5]、 约束型多波段选择[6]和信噪比[7]等算法。 秩统计方法根据秩统计指标, 选择信息量最大或相关性最小的波段, 形成特征波段子集, 并没有详细考虑光谱波段对物种的可识别性。 聚类统计方法则包括K-means聚类算法[8]、 基于密度的聚类算法[9]、 基于图的聚类方法[10]等。 上述聚类方法能有效地删除冗余波段, 但大多没有考虑整体性能, 不能最大化地保留物种信息, 且容易受到噪音的干扰。

随着计算机优化智能算法的发展, 一系列深度学习和基于搜索的智能优化算法成为高光谱特征波段选择的主流。 深度学习方法的波段选择是自动化的波段选取方法, 包括, 基于卷积网络方法[11], 基于注意力的方法[12], 基于表示学习方法[13]等, 没有任何的人工推理, 运算效率较低, 且被选的波段, 缺乏可解释性。

近年来, 为改进高维度数据中的特征选择性能, 研究者结合传统波段选择方法, 开发了许多智能优化搜索算法, 如, 人工蚁群优化[14], 粒子群优化[15], 遗传算法[2, 3]等。 这些算法的搜索空间相对大, 没有本质上减少搜索空间的维度, 影响了种群的搜索效率, 计算代价非常高。 遗传算法(genetic algorithm, GA)是一种流行的群智能优化技术, 能平衡全局探测和局部搜索, 已被应用于高光谱特征选择[2, 3]。 传统的遗传算法一定程度上提高了搜索效率, 但迭代次数较大, 收敛速度慢, 容易陷入局部极端值。 量子遗传算法(quantum genetic algorithm, QGA)引入了量子理论, 遵循大自然的基本运行规律, 使遗传进化操作能更有效地继承种群中最佳个体的属性。 种群更新过程也保证了个体多样性, 可避免陷入局部优化[16, 17]。 量子遗传算法已广泛应用于影像分割、 任务调度、 聚类、 组合优化等多种优化问题[18], 但针对高光谱波段优化选择的研究相对匮乏。

目前, 高光谱遥感影像尚未进入普适阶段, 特征波段选取研究多针对共享高光谱影像库(如, Indian Pines, KSC, Botswana, Salinas等)中的影像, 首先通过波段运算选取特征波段, 而后利用选取后的特征波段进行分类验证[12, 13]。 上述方法未针对特定的生态环境应用问题, 多为方法探讨类研究, 具有一定的局限性。 针对特定应用问题的研究, 则多以实测高光谱曲线为基础[2, 3], 结合不同的分类方法, 选取适用于特定生态问题的高光谱特征波段。 光谱角绘图(spectral angle mapper, SAM)是一种快速绘制影像光谱与参考光谱相似度的工具[19], 已广泛应用于高光谱及多光谱分类中[20, 21], 取得良好的效果。

本研究立足鄱阳湖湿地植被精细分类问题, 采用实测高光谱数据, 基于k近邻光谱角分类方法(spectral angle mapper based k-nearest neighbors classifier, KNN-SAM), 引入量子遗传算法, 改进基于传统遗传光谱角分类方法, 提出基于量子遗传光谱角分类(QGA-KNN-SAM)的高光谱植被特征波段选取方法, 为鄱阳湖湿地植被精细分类提供方法支撑, 对其他同类研究具有一定的借鉴意义。

1 实验部分
1.1 研究区

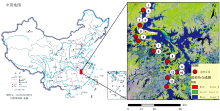
鄱阳湖(28° 22'— 29° 45'N 和 115° 47'— 116° 45'E)是中国最大的内陆淡水湖, 位于长江南岸, 是长江流域典型的吞吐性湖泊(图1)。 “ 洪水一片, 枯水一线” 是鄱阳湖水面面积变化过程中最形象的写照。 受亚热带季风气候的影响, 鄱阳湖水面面积70%的年份1~7月份波动上升, 其湿地植被亦被陆续淹没于浩翰的湖水之中。 洪水期过后, 8月— 12月湿地植被随着水位的降低再次萌芽并蓬勃生长。 根据多年观测发现, 鄱阳湖湿地植被上半年和下半年优势物种在不同的区域时有变化, 在极端气候条件下其变化更为明显。

图1 研究区内湿地优势植物物种采样点位分布图Fig.1 Sampling points of the study area for dominant wetland vegetation species

1.2 数据

本研究以2023年上半年鄱阳湖湿地优势物种, 包括苔草、 南荻、 虉草、 看麦娘、 芦苇、 藜蒿、 青蓼、 风花菜、 长刺酸模、 紫云英等物种为主要研究对象, 采用便携式地物光谱仪(SVC HR1024), 获取上述10种湿地挺水植物的高光谱数据。 SVC HR1024光谱仪的光谱波段范围为350~2 500 nm, 光谱分辨率为3.5~8.5 nm。

光谱实地测量沿鄱阳湖主湖西岸及主要碟形湖周边, 自北(星子落星墩)至南(军山湖入江通道)设置13个实验样区(图1), 每个样区采样范围为1 km范围内, 针对实验样区的优势物种采集不低于10组光谱曲线。 每个样区的优势物种及研究中所用的高光谱数据分布见表1, 该光谱数据获取时间为2023年4月15日— 17日, 上午9:00— 11:00, 下午2:00— 4:30。 2023年4月15日— 16日晴朗无云, 17日晴见少云。

表1 试验区各样区的优势植物物种及光谱数量 Table 1 Dominant vegetation species of the study area and the volume of spectral data for each species
1.3 光谱数据预处理

原始光谱曲线的波长926~981 nm为太阳辐射光谱水汽的弱吸收区[图2(a)A], 而1 800~1 954 nm为水汽和CO2的强吸收区[图2(a)B], 因此, 这两个区间光谱波动较大。 对应水汽和CO2的强吸收区采用高斯过程回归进行模拟处理[图2(a)和(b)B], 最后采用Savitzky-Golay滤波对350~2 500 nm区间的光谱进行平滑处理[图2(c)A和C]。 考虑不同时刻测量的光谱曲线可能受太阳高度角及大气条件的影响, 对模拟和光滑处理后的实测光谱进行了归一化处理[图2(d)]。 在后续研究中对比分析了原始光谱和归一化光谱两种情况下, 10种湿地植被类型特征波段的选取结果。

图2 光谱预处理对比图(以南荻的五条光谱曲线为例)
(a): 原始高光谱; (b): 高斯过程回归处理后的光谱; (c): 平滑处理后的光谱; (d): 归一化处理后的光谱Fig.2 Preprocessing comparison of spectra (Take Miscanthus sacchariflorus as an example)
(a): Original; (b): Gaussian process regression; (c): Gaussian process regression and smoothing; (d): Gaussian process regression, smoothing and normalization

1.4 方法

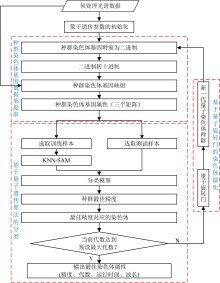
采用Han和Kim提出的基于量子比特和量子态叠加特性的遗传量子算法[16], 将量子的态矢量表达引入遗传编码, 利用量子旋转门实现染色体的进化, 进而提高基于KNN-SAM分类方法的精度, 并确定最优染色体的光谱基因组合(图3)。 量子遗传光谱角分类算法(QGA-KNN-SAM)主要包含: 量子遗传参数的初始化, 种群染色体基因数据集提取, 基于量子遗传算法的KNN-SAM分类, 以及基于量子旋转门的染色体演化等四个关键技术。

图3 量子遗传光谱角分类算法流程图Fig.3 Flow chart of quantum genetic spectral angle mapper algorithm

1.4.1 量子遗传参数的初始化

量子遗传算法是从种群(Population)开始, 每一代种群由多个量子染色体(Chromosome)组成, 每个量子染色体由多个量子基因组成, 每个量子基因又通过多个量子比特构成。 因此, 量子遗传算法中, 种群染色体个数(number of chromosomes, NC), 染色体中基因个数(genes number, GN), 基因中量子比特个数(Q-bit number of gene, QNG)以及最大遗传代数(maximum number of genetic generation, MGG)等参数需要设定。 物种的每个高光谱反射数值对应一个量子基因, 因此所有参数设置取决于预处理后的物种高光谱反射数据。

(1) 种群染色体个数(NC): 为使量子遗传算法进行启发式搜索时避免陷入局部优化, 并与传统遗传算法[2, 3]公平地比较, 需设定NC为一个较大的整数。 然而, 为使算法对应的程序运行时间恰当, NC不能太大。 通过实验对比和均衡考虑, 我们取NC=1 000。

(2) 染色体中基因个数(GN): 通过单个染色体中不同基因个数的计算性能的对比实验, 发现量子遗传算法中精度在85%以上的最小基因数为4, 即GN=4。

(3) 基因中量子比特个数(QNG): 经过一次观测, 每个高光谱量子基因, 坍缩为QNG个二进制比特。 根据预处理后物种的高光谱反射数据个数895(29< 895< 210), 至少需采用10位二进制比特才能有效表示895个不同的反射率数据序号, 即QNG=10。

(4) 最大遗传代数(MGG): 实验发现, 量子遗传算法设置100代, 可以达到高精度, 而略超过100代, 精度不会有明显提高。 基于运算性能考虑, 设置MGG=100。

1.4.2 种群染色体基因数据集提取

种群染色体基因数据集的提取是基于量子遗传光谱角分类算法的高光谱植被特征波段选取的基础。 为了实现二进制比特数据和染色体基因数据的转化, 首先需要将每个染色体基因的QNG个二进制比特转为一个十进制数, 建立种群染色体基因映射; 而后, 利用上述映射, 提取种群染色体基因数据, 包括高光谱反射率数据对应的序号、 光谱波长以及高光谱反射率等, 构建种群染色体基因数据集, 为后续样本选取奠定基础。

1.4.3 基于量子遗传算法(QGA)的KNN-SAM分类

在光谱特征空间中, 光谱角绘图(SAM)算法将目标光谱与参考光谱作为一个n维度的向量, 计算目标光谱和参考光谱向量之间的角度, 根据角度的大小确定其相似性[19]。 光谱角越小, 匹配度越高, 同一类的可能性也越大[3], 反之亦然。 SAM采用COSIN函数(cos-1)计算向量间的光谱角度[式(1)], 范围为0° ~90° 。

SAM=cos-1ab‖a‖‖b‖(1)

式(1)中, a和b分别为目标光谱向量和参考光谱向量。

前期研究发现: 在相同训练样本和测试样本情况下, KNN-SAM的分类精度较高[2, 3]。 所以, 采用基于SAM的k近邻分类器(KNN-SAM), 计算种群中每个染色体的分类精度值, 作为种群中每个染色体的适应度值。

由于量子遗传算法的随机性, 为了获得最佳精度的染色体, 量子遗传算法迭代100次, 循环运行30次, 输出30次运行结果的最佳染色体的属性, 并进行统计分析。

1.4.4 基于量子旋转门的染色体演化

量子旋转门通过旋转角度θ 的变化, 改变量子比特的状态[16, 22], 实现量子遗传算法中种群染色体更新[式(2)]。

α'β'=cosθ-sinθsinθcosθ×αβ(2)

式(2)中, θ 为量子旋转角度, αβ为一个原始量子比特, α'β'为一个新的量子比特。

1.4.5 特征波长基因的聚类分析

根据QGA-KNN-SAM算法可知, 每运行100代, 算法会输出一个最佳染色体, 即4个特征波长基因。 运行30次后, 我们可获得120个特征波长基因。 这些特征波长的分布可能会遵循某种特征规律, 采用K中心点聚类算法[23], 对上述特征波长基因中心点进行聚类分析, 将120个特征波长基因数据集合, 划分为K数目的同构组, 每个组可组合为一个特征波段。 根据光谱特征的分布规律, 本研究将特征波长基因划分为6个同构组, 即K=6。

2 结果与讨论

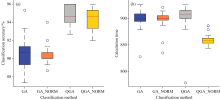
基于实测原始高光谱数据和归一化高光谱数据, 训练样本和测试样本的比例设置为1∶ 1, 利用本研究提出的QGA-KNN-SAM算法, 经过30次, 迭代100代的循环运算, 可获得不同数据支撑下分类精度和运算时间等计算性能参数[图4(a)和(b)], 以及适用于高光谱植被精细分类特征波长基因[图5(a)和(b)中的圆点]。 基于运算所得的特征波长基因, 利用K中心点聚类方法, 可计算出不同特征波长基因同构组, 即特征波段(表2)。

图4 基于原始光谱(QGA和GA)和归一化光谱(QGA_NORM和GA_NORM)的遗传学光谱角分类计算性能箱形对比图
(a): 分类精度; (b): 运行时间Fig.4 Calculation performance comparison of genetic spectral angle mapper based on original (QGA and GA) and normalized spectrum (QGA_NORM, GA_NORM)
(a): Classification accuracy; (b): Calculation time

图5 湿地植被特征波长基因聚类结果和多源卫星影像的波段分布(灰盒和白盒)
(a): QGA; (b): QGA_NORM; (c): GA; (d): GA_NORMFig.5 Band distribution of multi-source satellite images (grey box and white box) and feature wavelength gene clustering results of wetland vegetation
(a): QGA; (b): QGA_NORM; (c): GA; (d): GA_NORM

表2 特征波长基因聚类分析族群的波长范围和质心(nm) Table 2 The wavelength range and centroid of feature wavelength gene clustering analysis (nm)
2.1 计算性能

从QGA-KNN-SAM算法的总体性能看, 针对归一化高光谱数据的计算性能高于针对实测原始高光谱的计算性能。 从QGA-KNN-SAM算法的分类精度来看, 针对实测原始高光谱的分类精度在94%~96%之间变动, 而针对归一化高光谱数据的分类精度在93%~95%之间变动, 但平均分类精度相差无几[图4(a)QGA和QGA_NORM]。 针对归一化高光谱数据的平均计算时间[图4(b)QGA_NORM], 则明显低于针对实测原始高光谱的计算时间。 图4(a)和(b)中QGA为基于原始光谱数据的量子遗传光谱角分类算法; GA为基于原始光谱数据的传统遗传学光谱角分类算法; QGA_NORM为基于归一化光谱数据的量子遗传光谱角分类算法; GA_NORM基于归一化光谱数据的传统遗传光谱角分类算法。

2.2 特征波长基因及波段

从特征波长基因分布和特征波段看, 归一化高光谱数据的特征波长比原始高光谱数据的特征波长分布更为集中, 特征波段带宽也更窄。 基于原始高光谱数据的特征波长基因分布相对分散, 从蓝绿色可见光(395.7 nm)到近红外及中远红外波段(2 149.2 nm)均有分布。 针对归一化高光谱数据的特征波长基因则主要分布于绿光(514.4 nm)到近红外波段(1 791.8 nm)[图5(a)和(b), 表2]。 针对原始光谱曲线的特征波段带宽11.8~165.5 nm, 特征波段总跨度为634.4 nm; 归一化光谱曲线的特征波段宽度则为25.9~231.5 nm, 特征波段总跨度为589 nm(表2)。 本工作所使用的两类高光谱数据, 两种遗传算法提取的特征波长基因在1 800~1 954 nm强水汽和CO2的吸收区均无分布。 图5(a— d)中, QGA为基于原始光谱和量子遗传算法的KNN-SAM算法; QGA_NORM为基于归一化光谱和量子遗传算法的KNN-SAM算法; GA为基于原始光谱和传统遗传算法的KNN-SAM算法; GA_NORM为基于归一化光谱和传统遗传算法的KNN-SAM算法。

早在2007年Vaiphasa等便提出了GA-KNN-SAM算法用于识别植被精细分类的波段选择算法[2], 并应用于其他材料精细分类的波段选择中[3], 取得良好效果。 为了验证本文提出的QGA-KNN-SAM算法的有效性, 我们利用同样的数据组合, 采用GA-KNN-SAM算法获取波段选择结果, 并与QGA-KNN-SAM的计算结果进行对比分析, 判断QGA-KNN-SAM算法的性能。

实验环境的硬件为DELL Precision 7820计算机 , 软件操作系统为Windows 10, 程序开发环境为Matlab 2021a。

2.3 计算性能的对比

基于QGA-KNN-SAM算法的计算性能明显高于GA-KNN-SAM算法。 从分类精度来看, 针对实测原始高光谱和归一化高光谱数据的QGA-KNN-SAM算法, 其分类精度高于GA-KNN-SAM算法的分类精度。 基于归一化高光谱数据和原始高光谱数据, 利用GA-KNN-SAM算法进行分类, 多次迭代的分类精度变化范围, 归一化高光谱数据的变化范围略小于原始高光谱数据的变化范围。 QGA-KNN-SAM算法的分类精度变化范围, 尤其是平均精度则相差无几[图4(a)]。

对比四种组合的计算时间可以发现: 针对原始高光谱数据的QGA-KNN-SAM平均计算时间[图4(b)QGA]略高于GA-KNN-SAM算法; 针对归一化高光谱数据的QGA-KNN-SAM平均计算时间[图4(b)QGA_NORM], 则明显低于其他三种组合。 总体而言, QGA-KNN-SAM算法的计算性能明显优于GA-KNN-SAM算法。

2.4 特征波长及波段分布特征对比

从适用于高光谱植被精细分类特征波长基因(图5)和特征波段(表2)的分布特征不难发现: 基于QGA-KNN-SAM算法的特征波长基因相较于基于GA-KNN-SAM算法的特征波长基因分布相对集中, 特征波段带宽更小, 相较于现有的多光谱及高光谱数据(如, Landsat TM/OLI, MODIS, Sentinel 2A, HJ-1B, GF-5), 其波段及带宽针对性更强。 GA-KNN-SAM算法的特征波长基因从蓝色可见光(352 nm)到短波红外(2 303 nm)均有分布, 且基于原始光谱曲线的特征波长基因分布比基于归一化光谱曲线的特征波长基因更为分散[图5(c)和(d)]; 基于GA-KNN-SAM算法的特征波段带宽更大, 针对原始光谱曲线的特征波段宽度118.8~310.7 nm, 而基于归一化光谱曲线的特征波段宽度则为136.1~310.2 nm(表2)。 基于QGA-KNN-SAM算法的特征波长基因分布聚集度相对较高(2.2部分)。 总之, 基于归一化高光谱曲线和QGA-KNN-SAM算法的特征波段覆盖范围在4种组合中最小, 指向性最强。 基于原始高光谱曲线和QGA-KNN-SAM算法的特征波段覆盖范围次之, 但相较于GA-KNN-SAM算法的特征波段指向性较高。

基于两类数据, 两种方法的群组质心点的分布特征具有一致性, 即, 基本均分布于光谱曲线峰值前后(图6), 且多种物种间的光谱差异亦差异较小(表2)。 结合GA和QGA算法中的特征波长随机性特征, 质心点的分布特征亦具有一定的随机性。 因此, 分析的关键在于特征波长区间的聚焦特征。 基于归一化光谱的QGA-SAM算法的聚集性更强, 更利于确认现有卫星遥感数据各波段的有效性(图5和图6)。 与传统植被解译方法不同, 湿地植被的精细分类中需要考虑蓝、 绿可见光反射特征, 植被的红外光谱特征, 1 400 nm左右的卷云波段以及2 000 nm左右反应水文特征的短波红外特征。

图6 基于不同光谱类型的QGA-KNN-SAM和GA-KNN-SAM方法计算的质心点分布
(a): 原始光谱; (b): 归一化光谱Fig.6 Centroid distribution based on QGA-KNN-SAM and GA-KNN-SAM using original and normalized spectral data
(a): Original spectra; (b): Normalized spectra

3 结论

本研究立足鄱阳湖湿地物种的精细分类问题, 引入量子遗传算法, 采用KNN-SAM分类方法, 精确地获取特征波长和波段, 其运算效率明显高于传统遗传算法[2, 3]。 同时, 该算法通过循环迭代运算, 可获取多种特征波长基因的组合, 通过设置聚类分析参数可同时给出特征波段的带宽、 最大、 最小波长及波长质心。 前期针对特定应用的特征波长或波段选取研究中, 以中心波长指导多光谱及高光谱数据选取或压缩[1, 2, 3], 难以从理论上确定被选波段的有效性。 该算法选取的特征波长及波段指向性或聚集度较高, 可用于指导针对精细分类中多源、 多光谱遥感数据波段的选择, 及高光谱数据的压缩, 为高光谱数据压缩提供理论支撑, 为被选波段提供物理解释。

针对上述四种组合方法, 特征波长基因在水汽和CO2吸收区均无分布, 说明针对光谱数据进行的预处理方法, 不会对特征波长基因和特征波段的分布产生影响。 湿地植被精细分类中, 要考虑反应水文信息和植被反射信息的波段。 该算法可广泛应用于植被物种、 自然或人工材料及岩石类型等需要高光谱精细分类的特征波长和波段的选择研究, 弥补量子遗传算法在高光谱特征波长和波段选择方面的缺失, 拓展了量子遗传算法的应用范围。

为了对比分析QGA-KNN-SAM和GA-KNN-SAM算法的计算性能, 我们采用了相同数据、 相同迭代次数, 并未设置与精度有关的终止条件。 如果要将该算法应用于海量高光谱数据的处理和选取, 则需要在后续的研究中根据不同的应用问题设置精度驱动的算法终止机制, 进一步提升QGA-KNN-SAM算法的运算效率。

参考文献
[1] Song G, Wang Q. Ecological Informatics, 2023, 76: 102141. [本文引用:2]
[2] Vaiphasa C, Skidmore A K, Boer W F, et al. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 62(3): 225. [本文引用:9]
[3] Ullah S, Shakir M, Iqbal M S, et al. Ecological Informatics, 2021, 64: 101362. [本文引用:10]
[4] Varade D, Maurya A K, Dikshit O. International Journal of Remote Sensing, 2019, 40(20): 8031. [本文引用:1]
[5] Guo B F, Gunn S R, Damper R I, et al. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 522. [本文引用:1]
[6] Li H C, Chang C I, Wang L, et al. Constrained Multipler Band Selection for Hyperspectral Imagery, IEEE International Geoscience and Remote Sensing Symposium, IEEE, 2016. [本文引用:1]
[7] Yarra C, Nagesh S, Deshmukh O D, et al. Journal of the Acoustical Society of America, 2019, 146(3): 1615. [本文引用:1]
[8] Yuan Y, Lin J, Wang Q. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(3): 1431. [本文引用:1]
[9] Cao X, Wu B, Tao D, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(9): 4352. [本文引用:1]
[10] Li S, Qiu J, Yang X, et al. Engineering Applications of Artificial Intelligence, 2014, 27: 241. [本文引用:1]
[11] Feng J, Chen J, Sun Q, et al. IEEE Transactions on Cybernetics, 2020, 51(9): 4414. [本文引用:1]
[12] He K, Sun W, Yang G, et al. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 3169018. [本文引用:2]
[13] Wang J, Tang C, Liu X, et al. IEEE Transactions on Cybernetics, 2023, 53(8): 5250. [本文引用:2]
[14] He C, Zhang Y, Gong D, et al. IEEE Transactions on Evolutionary Computation, 2022, 26(6): 1566. [本文引用:1]
[15] ZHANG Liu, YE Nan, MA Ling-ling, et al(张刘, 叶楠, 马灵玲, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(10): 3194. [本文引用:1]
[16] Han K H, Kim J H. IEEE Transactions on Evolutionary Computation, 2002, 6(6): 580. [本文引用:3]
[17] Zhang B, Chen S, Gao S, et al. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1000112. [本文引用:1]
[18] Gharehchopogh F S. Artificial Intelligence Review, 2023, 56(6): 5479. [本文引用:1]
[19] Kruse F A, Lefkoff A B, Boardman J W, et al. Remote Sensing of Environment, 1993, 44(23): 145. [本文引用:2]
[20] Liu D, Han L. International Journal of Pattern Recognition and Artificial Intelligence, 2022, 36(1): 2254002. [本文引用:1]
[21] Agrawal N, Govil H, Mishra G, et al. Remote Sensing, 2023, 15(12): 3133. [本文引用:1]
[22] Alam T, Raza Z. Journal of Systems and Software, 2018, 135: 126. [本文引用:1]
[23] Huang D, Wang C D, Wu J S, et al. IEEE Transactions on Knowledge and Data Engineering, 2020, 32(6): 1212. [本文引用:1]