引用本文
王雪, 王子文, 张广月, 马铁民, 陈争光, 衣淑娟, 王长远. 基于迁移成分分析的近红外光谱定量分析通用模型[J]. 光谱学与光谱分析, 2024,44(11): 3213-3221.
WANG Xue, WANG Zi-wen, ZHANG Guang-yue, MA Tie-min, CHEN Zheng-guang, YI Shu-juan, WANG Chang-yuan. A Universal Model for Quantitative Analysis of Near-Infrared Spectroscopy Based on Transfer Component Analysis[J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3213-3221.
Doi:10.3964/j.issn.1000-0593(2024)11-3213-09  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于迁移成分分析的近红外光谱定量分析通用模型
王雪1,2,4, 王子文1, 张广月1, 马铁民1, 陈争光1, 衣淑娟3,4, 王长远2
1.黑龙江八一农垦大学信息与电气工程学院, 黑龙江 大庆 163319
2.农业农村部农产品及加工品质量监督检验测试中心(大庆), 黑龙江 大庆 163319
3.黑龙江八一农垦大学工程学院, 黑龙江 大庆 163319
4.黑龙江省水稻生态育秧装置及全程机械化工程技术研究中心, 黑龙江 大庆 163319

作者简介: 王 雪, 女, 1980年生, 黑龙江八一农垦大学信息与电气工程学院副教授 e-mail: mtmwx@163.com

收稿日期: 2023-12-18 修回日期: 2024-06-12
基金: 国家自然科学基金项目(52275246), 黑龙江省自然科学基金项目(LH2022C061), 黑龙江省博士后科研启动基金项目(LBH-Z19217), 黑龙江八一农垦大学三横三纵支持计划项目(ZRCQC201907)和黑龙江八一农垦大学学成人才科研启动基金项目(XDB202004)资助
摘要

在近红外光谱定量分析中, 由于光谱数据采集设备和环境条件的不同, 已有模型在使用到不同设备或不同环境时会出现预测精度低的现象。 为了增强定量分析模型的普适性和通用性, 提高模型的预测精度, 提出一种基于改进的迁移成分分析转移方法(TM-TCA)的近红外光谱定量分析通用模型构建策略。 改进的迁移成分分析方法采用二次校正策略, 通过对从机光谱数据的两次校正, 改善由于仪器偏移、 漂移或不稳定性引起的光谱差异性, 确保数据的一致性和准确性, 消除仪器不同或外界条件影响产生的偏差, 使校正后的从机光谱数据特征尽可能接近主机光谱, 以此增强模型对从机光谱的预测能力。 首先求出主机与从机光谱转换矩阵, 通过转换矩阵进行待测样品的一次校正, 缩小主机与从机样品间受外界条件因素产生的差异性。 将经过转换矩阵转换后的主机-从机光谱数据矩阵作为迁移成分分析方法的输入。 接下来, 基于多指标综合迭代优化选择迁移学习中的核函数和特征值个数的基础上构建定量分析通用模型。 为了验证迁移成分分析改进效果, 与多种方法的转移效果进行比较。 通过优化分析选择RBF核函数, 特征值个数为52, 实验表明, 基于TM-TCA的光谱校正率达到97.1%, 光谱平均差异(ARMS)与转移前相比下降了82.9%, 比TM和TCA方法分别降低了46.5%和30.2%。 为了验证模型构建策略的有效性, 构建基于TM-TCA和偏最小二乘回归(PLSR)的玉米水分定量分析通用模型, 并对不同设备条件下的模型通用性进行分析。 TM-TCA-PLSR模型的预测效果与TCA-PLSR模型的预测效果相比较, 模型的预测决定系数达到了0.872 9, 提升了41%, 预测均方根误差(RMSEP)和平均绝对误差(MAE)分别为0.154 3和0.115 9, 均降低了90%以上, 并且TM-TCA-PLSR模型相对分析误差(RPD)值超过了2.5, 模型具有实际应用的价值。 表明了TM-TCA转移方法能有效减少主机和从机光谱之间的差异性, 基于TM-TCA和PLSR的主机模型具有一定的通用泛化能力。

关键词: 近红外光谱; 定量分析; 模型转移; 迁移成分分析
中图分类号:O657.33 文献标志码:A
A Universal Model for Quantitative Analysis of Near-Infrared Spectroscopy Based on Transfer Component Analysis
WANG Xue1,2,4, WANG Zi-wen1, ZHANG Guang-yue1, MA Tie-min1, CHEN Zheng-guang1, YI Shu-juan3,4, WANG Chang-yuan2
1. College of Electrical and Information, Heilongjiang Bayi Agricultural University, Daqing 163319, China
2. Daqing Center of Inspection and Testing for Agricultural Products and Processed Products, Ministry of Agriculture and Rural Affairs, Daqing 163319, China
3. College of Engineering, Heilongjiang Bayi Agricultural University, Daqing 163319, China
4. Heilongjiang Province Research Center of Ecological Rice Seedling Raising Device and Whole Course Mechanized Engineering Technology, Daqing 163319, China
Abstract

There are differences in spectral data acquisition equipment and environmental conditions. In near-infrared spectroscopy quantitative analysis, low prediction accuracy was found in the models established. To enhance the universality and generalizability of near-infrared spectroscopy quantitative analysis models and improve their predictive accuracy, a universal model strategy is proposed based on the transfer component analysis method improved by the transfer matrix (TM-TCA). The TM-TCA method adopts a two-step correction strategy to correct the slave spectral data, reducing the spectral differences caused by instrument offsets, drifts, or instabilities. It can make the characteristics of the corrected slave spectral data similar to the master's to the maximum extent, eliminate the deviation caused by different instruments or external conditions, and enhance the prediction ability of the model to the slave spectral data. Firstly, the spectral transfer matrix between the master and the slave is obtained. The transfer matrix converts the master-slave spectral data matrix, which is then used as the input for the transfer component analysis method. Subsequently, the kernel function and the number of eigenvalues in transfer learning are chosen using iterative optimization of multiple indicators. The RBF kernel function is selected, and the number of eigenvalues is 52. Comparative experiments are conducted with other methods to verify the effectiveness of TM-TCA. The experimental results show that the spectral correction rate based on TM-TCA reaches 97.1%, with a reduction of 82.9% in the average relative mean squared (ARMS). The ARMS value surpasses that achieved by the transfer matrix and TCA methods, 46.5% and 30.2%, respectively. To validate the effectiveness of the model construction strategy, a universality quantitative analysis model is established based on TM-TCA and partial least squares regression (PLSR) under different device conditions. Compared to the prediction performance, the TCA-PLSR model's coefficient of determination of the TM-TCA-PLSR model reaches 0.872 9, which is improved by 41%. The root-mean-square error of prediction (RMSEP) and the mean absolute error (MAE) are 0.154 3 and 0.115 9, respectively, reduced by more than 90%. Furthermore, the relative prediction determination (RPD) of the TM-TCA-PLSR model exceeds 2.5, indicating that the model has practical application value. The experimental results demonstrate that the TM-TCA transfer method reduces the difference between the master and slave spectra. The master model established based on TM-TCA exhibits a certain degree of universality capability.

Keyword: Near-infrared spectroscopy; Quantitative analysis; Model transfer; Transfer component analysis
引言

近红外光谱技术(near-infrared spectroscopy, NIRS)被广泛应用于食品、 农产品、 医药、 材料等领域[1, 2]。 近红外光谱仪的类型繁多, 普遍存在模型无法通用的问题。 为了保障检测结果的精确程度, 在更换设备或者环境的情况下, 检测模型需要重新训练或校正, 将增加时间和人力成本, 限制了近红外光谱技术的发展和应用推广[3]。 在近红外光谱实际应用中, 利用已有模型的知识和经验来快速满足新的检测需求是一个较好的选择。

随着人工智能的不断发展, 模型转移成为机器学习领域中一个重要的研究方向。 模型转移是指将一个已经训练好的模型应用到另一个应用的过程。 针对近红外光谱不同设备、 不同样本的通用问题, 诸多学者在模型转移方面进行了大量研究[4, 5]。 模型转移方法分为有标样和无标样模型转移, 而有标样模型转移算法应用更为广泛[6, 7]。 直接校正算法(direct calibration, DS)、 分段直接校正算法(piecewise direct standardization, PDS)以及横截距算法(slope and bias correction, S/B)算法等都是典型的有标样模型转移方法。 王红鸿等[8]采用具有稳定一致光谱信号的波长算法(SWCSS)和DS结合实现纸浆中纤维素模型的转移, 预测均方根误差下降了1.43%, 主机模型的普适性有了一定程度的提高。 温晓燕等[9]利用PDS结合偏最小二乘回归(partial least squares regression, PLSR)实现甲醇汽油的模型转移, 校正转移后从机预测性能显著提升, 决定系数R2可以达到0.99以上。 Xu等[10]构建基于一致稳定信号波长筛选法的近红外光谱通用模型, 在一定程度上提高了转移模型的效率。 Bai等[11]提出了一种融合全局建模法和校正传递法的组合模型校正策略, 在应用全局建模、 动态正交投影(dymamic orthogonalization projection, DOP)和斜率/偏差校正(slope/bias correction, SBC)方法对季节变量进行修正后, 模型的预测标准偏差降低了44.7%, 增强了模型的鲁棒性。 刘智健等[12]提出DS-PDS算法联用木质素近红外分析模型, 实现不同仪器之间模型转移, 从机决定系数最高可达0.96。 张进等[13]利用连续小波变换和半监督-无参数模型增强消除NIR光谱中背景漂移和样本依赖的时序信号漂移部分, 进而实现了准确建模, 该方法计算过程简单, 无需参数调整, 为时序漂移NIR光谱建模提供了一种有效的解决方案。

2011年, Pan等[14]基于边缘分布的最大均值差异度量, 提出了基于特征的迁移成分分析(transfer component analysis, TCA)算法, 该算法通过将主机光谱数据和从机光谱数据的特征映射到新的潜空间, 在特征降维的同时减小光谱数据之间的差异。 目前, 已广泛应用到故障分类、 病害识别等领域的通用模型构建。 曹鸿亮等[15]提出了基于TCA和支持向量机(support vector machine, SVM)的肝移植并发症预测方法, 对肝移植数据集迁移完成后在源领域上训练SVM, 对目标领域数据分类测试准确率提高了7.8%, 有效提升肝移植并发症的预测精度, 改善了小样本肝移植医疗数据集预测精度不足的缺陷。 郑文瑞等[16]基于TCA算法将皖南土壤速效磷预测模型迁移至皖北, 模型的R2由-0.19提升至0.79, 预测均方根误差(root-mean-square error of prediction, RMSEP)从1.04降低至0.44, 在一定程度上实现皖南土壤模型和皖北的模型通用。 Qiu等[17]采用TCA结合SVM对土壤污染等级进行分类, 在三种不同地方的土壤样本中, 每组交叉选择两种分别作为源域和目标域, 根据污染程度与污染物的不同, 构建18组不同的模型转移任务, 通用模型的预测精度平均提升了7.6%。 Tao等[18]用TCA方法研究不同地区土壤重金属污染预测模型的可迁移性, 基于TCA转移后R2提高了63%, 在一定程度上实现北方平原和保定地区土壤模型的通用。

通过以上分析可以看出, 经过迁移成分分析方法进行光谱数据处理后, 模型的通用性和预测精度都有了不同程度的提升, 但模型预测结果与实际需求仍存在一定差距。 因此, 针对通用模型精度较低问题, 提出基于改进的迁移成分分析方法的通用模型构建策略。 首先求出主机与从机光谱转换矩阵, 通过转换矩阵进行待测光谱数据的一次校正, 缩小主机与从机样品光谱之间因外界条件因素产生的差异性; 再将转换后的主机-从机光谱数据矩阵作为迁移成分分析方法的输入, 并在迁移学习的核函数和特征值个数建模最优分析的基础上构建基于PLSR的定量分析通用模型。

1 实验部分
1.1 相关理论和算法

1.1.1 迁移成分分析

迁移成分分析属于基于特征的迁移学习方法, 旨在使一个领域学习到的模型适应到另一个不同但相关的领域中。 假设存在一个特征映射φ , 使新特征空间内的两个不同数据集的边缘概率分布尽可能一致, 即P(φ (Xs))≈ P(φ (Xt))。 从而在尽量保证源域与目标域的内部属性不缺失的情况下使两者之间的距离最小化, 即两者之间差异达到最小。 以此为基础, 利用传统的机器学习方法, 以有标签的主机数据为训练数据对无标签的从机数据进行计算。 主机与从机映射后的距离D(Xs, Xt)如式(1)所示。 其中, Xs、 Xt为主机和从机数据; P(Xs)、 P(Xt)为主机和从机数据的边缘分布。

D(Xs, 　Xt)≈‖P(Xs)-P(Xt)‖(1)

TCA方法具体步骤如下:

步骤1: 输入主机光谱$X_s$和从机光谱$X_t$, 利用公式 L(i, j)=1n12xi, xj∈Xs1n22xi, xj∈Xt-1n1n2其他和文献[15]的式(7)计算, 得到TCA的度量矩阵L和中心矩阵H, 其中n1、 n2分别表示主机和从机的样本个数; 详见文献[15];

步骤2: 计算Xs和Xt的核矩阵K;

步骤3: 对(μ I+KLK)-1KHK求解, 选择M个最大特征值相关联的m个特征向量构造特征变换矩阵构造特征变换矩阵W, W即为特征变换向量的集合;

步骤4: 将核矩阵K与变换矩阵W相乘得到矩阵X* , X* 即为校正后的光谱数据。

1.1.2 改进的迁移成分分析方法

基于迁移成分分析的光谱数据在迁移过程中, 样本特性和环境条件引起的变量偏移, 会影响算法的准确性, 待测样本检测时, 将产生较大误差, 导致模型稳健性差。 因此考虑在原有方法的基础上引入矩阵转换作为迁移数据的预处理。

改进的迁移成分分析方法(transition matrix and transfer component analysis, TM-TCA)是对从机光谱数据进行两次校正。 TM方法对光谱数据进行一次校正, 改善由于仪器偏移、 漂移或不稳定性引起的光谱差异性, 确保数据的一致性和准确性, 消除仪器不同或外界条件影响产生的偏差。 将经过第一次校正的从机光谱数据基于核函数和特征值个数建模最优分析的TCA算法进行第二次校正, 使校正后的从机光谱数据特征尽可能接近主机光谱, 以此增强模型在不同设备和采集条件下对光谱的预测能力。

TM-TCA方法具体步骤如下:

步骤1: 输入主机转换集Xstrans、 从机转换集Xttrans, 利用公式TM=Xstrans· X ttrans-1, 对Xttrans矩阵进行逆运算并与Xstrans矩阵相乘, 得到转换矩阵;

步骤2: 将转换矩阵与从机预测集Xtval进行矩阵乘法运算, 消除样本间的主要误差, 得到校正后的从机光谱矩阵XtF;

步骤3: 输入主机训练集Xscal和XtF, 计算得到度量矩阵L和中心矩阵H;

步骤4: 建立参数测评模型, 确定迁移过程中的计算参数, 根据多指标综合迭代完成核函数和特征值个数的优选。 获得最优核函数和最大相关联特征值个数m;

步骤5: 计算Xscal和XtF的核矩阵K;

步骤6: 对(μ I+KLK)-1KHK求解, 构造特征变换矩阵W, W即为特征变换向量的集合;

步骤7: 将核矩阵K与变换矩阵W相乘得到矩阵X* , X* 即为最终校正后的光谱数据。

在上述算法中, 步骤1— 步骤2完成基于矩阵转换的从机光谱校正, 通过计算主-从机对应波长之间的差异, 建立主机光谱数据与从机数据的光谱差异转换矩阵, 利用该转换矩阵实现从机光谱预测集的一次校正, 缩小不同仪器采集光谱数据之间的差异。 步骤3— 步骤7是基于TCA的二次校正, 在步骤4中根据参数测评模型的评价指标, 优选了参数和核函数, 从而改进了TCA算法。 将光谱特征变换到统一的再生核希尔伯特空间, 通过缩小主机与从机边缘概率分布的距离来进一步减小主机-从机对应光谱特征之间的差异性, 实现从机光谱特征空间的样本数据降维的同时, 达到提升转移模型预测精度的目的, 以增强模型的通用性。

1.2 实验数据

为了说明模型的通用性, 实验数据选择Eigenvector Research公司的玉米公开数据集(http://www.eigenvector.com/data/Corn/index.html)。 其中, M5型号光谱仪作为主机, MP5型号光谱仪作为从机, 并选取其中的水分含量作为响应变量, 光谱数据的波长范围为1 100~2 498 nm, 波长取样间隔为2 nm, 共计700个波长。

1.3 模型评价参数

模型的评价参数选择平均绝对误差(mean absolute error, MAE)、 决定系数(determination coefficient, R2)、 预测均方根误差(root-mean-square error of prediction, RMSEP)、 预测标准偏差(standard error of prediction, SEP)和分析相对误差(relative prediction determination, RPD)评价模型的性能。 MAE越小表明预测结果越接近于真实值, R2值越大表明光谱信息与分析组分的相关性越好, RMSEP值越小表明预测性能越好, 模型转移的效果越好, SEP值越小表明所建模型的误差越小, RPD用来验证模型的稳定性和预测能力, RPD值越大表明模型稳定性越强。 选择光谱平均差异(average relative mean squared, ARMS)以及光谱校正率(Prcorrected)用于评价模型的转移效果, ARMS值越小, 表示两个不同的光谱仪测得的光谱差异越小, Prcorrected越大表示光谱迁移性能越好[19]。

$\text { ARMS }=\frac{1}{n} \sum_{i=1}^{n} \sqrt{\frac{1}{p} \sum_{i=1}^{p}\left|S_{2 \lambda}^{i}-S_{1 \lambda}^{i}\right|}$(2)

ARMS计算如式(2)所示。 其中, n为样品个数, p为波长数, S2λi为在第二个仪器上的第i个样品λ 波长处测得的光谱数据, S2λi为在第一个仪器上的第i个样品λ 波长处测得的光谱数据。

Prcorrected(%)=ARMSuncorrected2-ARMScorrected2ARMSuncorrected2×100(3)

Prcorrected值计算如式(3)所示。 其中, ARMSuncorrected为校正前的ARMS, ARMScorrected为校正后的ARMS。

2 结果与讨论
2.1 光谱预处理

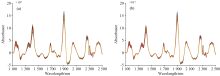
主机、 从机各包含80个玉米光谱样本数据, 每条样本光谱包含700个波长数据。 因未处理的近红外光谱数据中含有大量噪声, 会对模型的精度产生影响, 导致过拟合或精度过低。 对比标准正态变量转化法、 多元散射校正、 平滑处理以及一阶导数等不同预处理方法, 发现一阶导数预处理后模型的预测效果最好, R2值达到0.717 5, 更好地保留了玉米样本的光谱特征信息、 消除光谱背景干扰和减少光谱噪声。 主机与从机经过一阶导数预处理前后的光谱数据分别如图1和图2 所示。

图1 主机和从机采集的原始近红外光谱Fig.1 Raw NIR spectra of master and slave instruments

图2 一阶导数处理后的主机和从机近红外光谱Fig.2 NIR spectra of the master and slave instruments after first-order derivative processing

2.2 样本集划分

将主机光谱数据基于Kennard-Stone算法按照1∶ 1的比例进行划分。 其中, 主机转换集和从机转换集各包含40个光谱样本, 建模集为主机剩余40个样本, 预测集为从机剩余40个样本。 主机转换集与从机转换集一一对应, 建模集和预测集一一对应, 其中建模集化学性质含量的范围覆盖预测集的化学性质含量, 表明预测集可以对模型的性能进行验证。

2.3 转换矩阵的计算

计算主机转换集Xstrans与从机转换集Xttrans的函数关系。 通过转换矩阵TM对光谱进行第一次校正。 首先对Xttrans进行矩阵运算, 求其广义逆矩阵X ttrans-1, 由X ttrans-1与Xstrans可得出转换矩阵TM, 此时的转换矩阵TM代表着两台不同仪器采集样品的每一个波长的差异, 将转换矩阵TM应用于Xtval, 从而减小Xtval与Xscal之间的差异, 实现光谱一次校正, 得到XtF

XtF=Xttrans·TM=-6.39×10-5…-4.70×10-4………-1.22×10-4…-5.41×10-440×699·0.0162…-0.0326………-0.0001…-0.0983699×699=-1.72×10-4-9.88×10-4…-2.90×10-4-4.41×10-4-1.47×10-4-9.80×10-4…-2.52×10-4-3.72×10-4……………-1.44×10-4-1.03×10-4…-1.44×10-4-3.75×10-4-1.44×10-4-9.14×10-5…-1.89×10-4-4.49×10-440×699

运用转换矩阵将从机预测集样品光谱矩阵Xtval转换为校正后的光谱矩阵XtF后, 光谱差异值从0.011 06下降到了0.007 03。

2.4 参数迭代评价及选择

在TCA校正过程中, K矩阵的计算方式和特征值个数的确定, 对校正结果有很大的影响, 因此在TCA算法中加入参数选择机制是必要的。

K矩阵可以通过核函数计算获得, 也可以把主机与从机光谱矩阵转换为K矩阵。 为了实验的完整性, 分别选择线性核函数linear、 非线性映射函数RBF以及primal方式计算K矩阵。 primal方式将主机与从机光谱矩阵进行转置拼接, 再进行单位向量化后得到K矩阵。

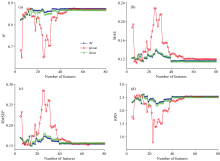
为了减小参数选择过多对模型效率带来的影响, 根据先验将核函数的宽度和正则化参数设置为10和2.0。 基于PLSR建立参数测评模型, 选择R2、 MAE、 RMSEP和RPD作为评价指标。 基于不同K矩阵计算方式、 不同特征值个数的测评模型的不同指标迭代结果如图3所示。

图3 TCA参数指标迭代结果Fig.3 TCA parameter tuning results

从图3中可以发现, 基于RBF核函数的测评模型与linear核函数和primal方式相比具有较高的稳定性。 在特征值个数的取值范围内, R2值均在0.82以上, 波动范围较小, 在(0.82, 0.87)之间; 而基于linear核函数和primal方式的测评模型在特征值个数小于40时波动范围较大, 尤其是primal方式, R2值最小达到0.53以下。 其他指标也具有相似的波动性, 特征值个数在40~80之间时波动性减弱, 紊定性增强。 RBF核函数和linear核函数的特征值个数大于40时趋于稳定, 而primal方式在大于50之后才趋于稳定。 从MAE值可以看出各评价指标的最佳值出现在基于primal方式和RBF核函数得到的K矩阵和特征值个数设置为52时, 校正后的从机预测集的R2值达到0.87以上, MAE值下降到0.12以下, RPD值达到2.5以上。 相比未经过校正的数据的预测模型的R2提升21%以上, RMSEP下降了89%以上。

primal方法的实验效果较好, 原因可能是原始光谱矩阵中的每个元素都直接参与到K矩阵的计算中, 能更好地捕捉数据相似性。 但是考虑到其可能无法充分挖掘数据中的非线性信息, 影响预测模型的稳定性, 而RBF核函数具有更好的泛化性能和适应性, 稳定性更好, 能够充分挖掘主机与从机之间的共享特征, 能够更好地捕捉光谱数据中的非线性关系, 在模型评价指标接近的情况下, 选择使用RBF核函数计算K矩阵。

综合以上分析, 选择RBF核函数计算K矩阵, 特征值个数设置为52。

2.5 光谱校正的实现及差异分析

采用2.4中选择的参数, 计算出K矩阵。 将主机光谱数据与一次校正后的从机光谱数据转换为稀疏矩阵, 对每个样本的特征向量进行单位向量化, 计算出L矩阵和H矩阵。 根据K矩阵对(μ I+KLK)-1KHK求解得到变换矩阵W。 变换矩阵W转置后与K矩阵相乘并进行单位向量化, 输出矩阵X* , 其中第41至80条数据为两次校正后的从机预测集。 X* 结果表示如下:

X* =KW=-0.0013…-0.0040………-0.0017…-0.005280×699·-5.55×10-4…-0.0245………-0.0038…0.0190699×52=-0.05050.0482…0.15720.0455-0.09810.0061…0.15580.0490……………0.0662-0.1650…0.15950.04920.1082-0.1400…0.16060.047980×52

建立基于PLSR的主机模型, 对两次校正后的从机预测集进行预测, 验证从机光谱与主机光谱数据的差异性变化和模型预测效果。 为了验证TM-TCA在光谱校正中的有效性, 在导数预处理的基础上, 将基于TM-TCA与TM、 TCA、 PDS、 DS、 S/B等常见的模型转移方法校正前后的光谱差异和转换率进行对比分析, 结果如图4所示。 校正前, 从机数据与主机数据的ARMS值为0.011 06。 PDS和SB方法校正后差异变大, 原因可能是PDS校正时会受到不同区域相似特征的影响, 而S/B方法会受到光谱数据非标准化的影响, 导致转移模型性能不稳定。 TM、 TCA、 DS方法校正后的ARMS值均有下降。 与校正前的ARMS值相比, TM、 DS方法校正后的ARMS值降低了36.4%, Prcorrected达到59.6%, TCA校正后的ARMS值降低了52.7%, Prcorrected达到77.6%。 说明DS方法、 转换矩阵和TCA校正方法都不同程度地减小了主机与从机之间的差异性。 TM-TCA方法校正后光谱差异最低, TM-TCA方法进行两次校正后的ARMS值仅为0.001 89, 比校正前降低了82.9%, Prcorrected则达到97.1%。

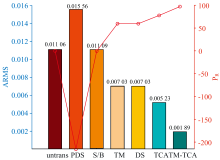图4 TM-TCA与传统方法校正后的光谱差异图Fig.4 Spectral differences between TM-TCA and conventional methods before and after correction

从ARMS值来看, TM-TCA比单一使用TM、 TCA方法校正的光谱数据分别降低了46.5%和30.2%, 校正效果最好, 说明该方法可以有效缩小从机光谱与主机光谱之间的差异, 体现了二次校正策略的优势。 一次校正弥补了TCA受校正样本与目标样本存在较大差异的影响, 二次校正采用TCA算法保留数据中的关键光谱特征并进行降维, 去除了光谱数据中存在的冗余信息, 减少了在第一次校正时受多个冗余或负相关波长点的影响, 从而进一步降低了光谱之间的差异。

从校正率来看, TM-TCA方法比单一使用TM、 TCA方法校正的光谱数据分别提高37.5%和19.5%。 与使用相同数据的其他文献进行对比也均有提升, 比杨辉华[19]提出的基于一元线性回归方法的Prcorrected提高了10.2%, 比王其滨[20]使用的随机森林与直接正交信号校正算法的Prcorrected提高了4.44%。 虽然样本划分比例与上述两个文献略有不同, 从模型校正效果上也能够体现TM-TCA方法对不同设备光谱校正的有效性。

总体可以看出, 基于TM和TCA方法的二次校正策略最大程度减少了主-从机光谱之间的差异, 提高了校正率, 校正效果提升明显。

2.6 模型通用性分析

为了验证模型构建策略的有效性, 构建主机基于TM-TCA和PLSR的玉米水分定量分析通用模型, 并进行对比分析, 结果如表1所示。

表1 基于不同转移算法的通用模型指标对比 Table 1 Comparison of prediction results of different model transmission algorithms

利用该模型预测从机未校正预测集样品的玉米种子水分含量, 模型的相关决定系数R2值仅为0.717 5, RMSEP值为1.492 9, MAE值为1.476 1, RPD值仅为0.262 1, 预测精度偏低, 误差较大, 说明未经过校正的从机光谱数据不能通过主机的定量分析模型来有效预测玉米种子中的水分含量, 模型不具备通用性。

与不同的传统模型转移方法建立PLSR模型进行对比。 可以看出, 基于传统转移方法所构建的模型与未转移的PLSR模型相比, 虽然误差均明显下降, 但是预测精度提升效果不明显。 效果最好的PDS方法R2仅提升了3.2%, RMSEP值下降了85.4%, 但是RPD值不足1.8。 基于TM-TCA方法的PLSR模型不仅误差明显小于其他模型还提高了从机光谱数据预测的精度, 比其他方法中效果最好的PDS方法R2提升了16.9%, RMSEP值下降了29.3%, RPD值超过了2.5。

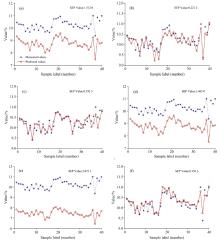
基于不同转移方法的PLSR模型预测结果对比如图5所示。 可以看出, 未校正的PLSR模型、 基于S/B和TCA的PLSR模型预测值与实际值的误差较大, 实际值和预测值的标准偏差数值分别达到了1.4和2.8以上, 基于PDS、 DS和本文提出的TM-TCA方法的PLSR模型的预测结果相对较好, 实际值和预测值的标准偏差均在0.25以下, 基于TM-TCA的定量分析模型的预测标准偏差最低, 达到0.16以下。 基于TM-TCA的定量分析模型的SEP值与杨辉华等[18]使用基于一元线性回归转移方法所建模型相比下降了37.9%。

图5 基于不同转移方法的PLSR模型预测结果
(a): 未转移的PLSR模型; (b): PDS+PLSR; (c): DS+PLSR; (d): S/B+PLSR; (e): TCA+PLSR; (f): TM-TCA+PLSRFig.5 Prediction results of model transfer methods
(a): PLSR of untransfered data set; (b): PDS+PLSR; (c): DS+PLSR; (d): S/B+PLSR; (e): TCA+PLSR; (f): TM-TCA+PLSR

综合以上分析, TM-TCA方法处理后的数据, 预测模型精确度和稳定性均较好。 预测集的决定系数R2可以达到0.872 9, RPD值大于2.5, 证明模型具备一定的预测能力和稳健性, 基本能够满足模型的实际应用要求。 可以得出, 基于TM-TCA和PLSR的玉米水分定量分析模型具备一定的通用性。

3 结论

(1)提出了一种基于矩阵转换的迁移成分分析的光谱数据校正方法TM-TCA。 并将TM-TCA应用于不同设备采集的玉米水分近红外光谱数据集, 实验证明通过校正可以在一定程度上缩小不同光谱设备近红外光谱数据的差异, 校正后的ARMS值仅为0.001 89, 比校正前降低了82.9%, Prcorrected则达到97.1%。

(2)与DS、 PDS、 S/B、 TM和TCA等多种传统算法进行对比, TM-TCA方法的光谱校正率, 光谱平均差异以及模型预测精度等各项指标值均有提升, 能够较好地实现光谱数据校正。

(3)构建基于TM-TCA和PLSR的玉米水分定量分析模型, R2可以达到0.872 9, RPD值大于2.5, SEP值降低到0.156 3, 证明基于TM-TCA方法的玉米水分定量分析模型能够实现不同设备之间的模型通用。

参考文献
[1] NI Li-jun, XIAO Li-xia, ZHANG Li-guo, et al(倪力军, 肖丽霞, 张立国, 等). Journal of Instrumental Analysis(分析测试学报), 2018, 37(5): 539. [本文引用:1]
[2] CHU Xiao-li, SHI Yun-ying, CHEN Pu, et al(褚小立, 史云颖, 陈瀑, 等). Journal of Instrumental Analysis(分析测试学报), 2019, 38(5): 603. [本文引用:1]
[3] QIAO Chun-yan, ZHANG Xue-ru, ZHENG Wei-min, et al(乔春艳, 张雪茹, 郑卫民, 等). Science and Technology of Food Industry(食品工业科技), 2021, 42(22): 297. [本文引用:1]
[4] Workman Jr J. Applied Spectroscopy, 2018, 72(3): 340. [本文引用:1]
[5] HU Li-ping, HUANG Sheng-quan, TIAN Shu-hua, et al(胡丽萍, 黄生权, 田淑华, 等). Chemical Industry and Engineering Progress(化工进展), 2020, 39(8): 3263. [本文引用:1]
[6] PENG Dan, LI Lin-qing, LIU Ya-li, et al(彭丹, 李林青, 刘亚丽, 等). Spectorscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(6): 1828. [本文引用:1]
[7] ZHANG Jin, CAI Wen-sheng, SHAO Xue-guang (张进, 蔡文生, 邵学广). Progress in Chemistry(化学进展), 2017, 29(8): 902. [本文引用:1]
[8] WANG Hong-hong, WANG Ying, HUANG Hao-ran, et al(王红鸿, 汪莹, 黄浩冉, 等). Chinese Journal of Analysis Laboratory(分析试验室), 2023, 43(6): 864. [本文引用:1]
[9] WEN Xiao-yan, XU Yan-yan, LI Mao-gang, et al(温晓燕, 徐艳艳, 李茂刚, 等). Chinese Journal of Analytical Chemistry(分析化学), 2021, 49(10): 1758. [本文引用:1]
[10] Xu Z P, Zhang P F, Wang Q, et al. Infrared Physics & Technology, 2022, 123(1): 104120. [本文引用:1]
[11] Bai Y H, Fang Y L, Zhang B H, et al. Computers and Electronics in Agriculture, 2022, 198(6): 107073. [本文引用:1]
[12] LIU Zhi-jian, XIONG Zhi-xin, HU Yun-chao, et al(刘智健, 熊智新, 胡云超, 等). Chinese Journal of Analysis Laboratory(分析试验室), 2023, 021201(https://doi.org/10.13595/j.cnki.issn1000-0720.2023.021201). [本文引用:1]
[13] ZHANG Jin, YE Shi-zhu, WU Ai-jing, et al(张进, 叶世著, 吴艾璟, 等). Chinese Journal of Analytical Chemistry(分析化学), 2022, 50(9): 1391. [本文引用:1]
[14] Pan S J, Tsang I W, Kwok J T, et al. IEEE Transactions on Neural Networks, 2011, 22(2): 199. [本文引用:1]
[15] CAO Hong-liang, ZHANG Ying, WU Bin, et al(曹鸿亮, 张莹, 武斌, 等). Journal of Computer Applications(计算机应用), 2021, 41(12): 3608. [本文引用:3]
[16] ZHENG Wen-rui, LI Shao-wen, HAN Ya-lu, et al(郑文瑞, 李绍稳, 韩亚鲁, 等). Journal of Instrumental Analysis(分析测试学报), 2020, 39(10): 1274. [本文引用:1]
[17] Qiu Z J, Zhao S T, Feng X P, et al. Science of the Total Environment, 2020, 740: 140118. [本文引用:1]
[18] Tao C, Wang Y J, Cui W B, et al. Science of the Total Environment, 2019, 669: 964. [本文引用:2]
[19] YANG Hui-hua, ZHANG Xiao-feng, FAN Yong-xian (杨辉华, 张晓凤, 樊永显, 等). Chinese Journal of Analytical Chemistry(分析化学), 2014, 42(9): 1229. [本文引用:2]
[20] WANG Qi-bin, YANG Hui-hua, PAN Xi-peng, et al(王其滨, 杨辉华, 潘细朋, 等). Laser and Infrared(激光与红外), 2020, 50(9): 1081. [本文引用:1]