1.1.1 亚硝酸盐溶液配制

从含有0.492 8 g亚硝酸钠(NaNO₂)的1 000 mL溶液中取出20.00 mL, 并将其稀释至1 000 mL, 得到了含有0.2 mg· L^-1亚硝酸盐离子(NO₂-N)的溶液。 然后, 分别使用该方法配制0.02、 0.04、 0.06、 0.08、 0.10、 0.12、 0.14、 0.16、 0.18和0.20 mg· L^-1的亚硝酸盐标液^[1]。

1.1.2 光谱数据获取

选择0.02、 0.04、 0.06、 0.08、 0.10、 0.12、 0.14、 0.16、 0.18和0.20 mg· L^-1十种浓度的亚硝酸盐溶液。 使用型号为OCEAN-HDX-XR的微型光纤光谱仪(美国Ocean Optics公司)对亚硝酸盐溶液进行光谱数据的采集。 该光谱仪具有高分辨率、 高灵敏度、 紧凑便携和宽波长范围等特点, 被广泛应用于化学、 环境监测等领域。 使用DH2000光源, 该光源结合了氘灯和钨卤素灯两种光源, 可提供宽波长范围的光照, 同时具有较高的光强稳定性。 当进行光谱数据采集时, 光源预热时间为5 min, 光谱仪狭缝为10 μ m、 环境温度保持在0~40 ℃, 在相同的时间间隔下对每个浓度的亚硝酸盐溶液进行10次数据采集, 共计得到100条光谱数据。 后通过白板校正得到所采集的100条光谱数据下的光谱透射率值^[7], 白板数据是指利用光谱仪对去离子水(纯水)下的背景光谱进行测量所得到的信息。 校正计算公式如式(1)所示

MC=M0/Mw(1)

式(1)中, M₀为原始光谱数据; M_w为白板数据。

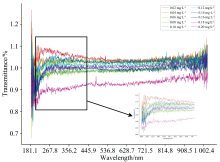
图1为白板校正后亚硝酸盐原始透射光谱图, 通过对该图进行分析可知, 不同浓度的亚硝酸盐光谱数据曲线存在细微的差异但趋势相似, 在光谱波段190~300 nm范围内, 光谱曲线呈上升趋势, 在300~800 nm范围内, 光谱曲线相对平稳, 图中220 nm波长周围处有极大的吸收峰, 不同浓度下的吸收峰之间存在差异, 主要表现为亚硝酸盐浓度越高, 该吸收峰处光谱透射率值越低。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 原始透射光谱Fig.1 Original transmission spectra

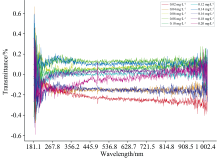
在进行光谱数据的采集时, 由于数据之间的量级、 均值点存在差异, 可能会导致模型性能和预测效果变差, 因此使用最大最小归一化和均值中心化两种数据预处理方法对原始透射光谱进行处理。 使用最大最小归一化将数据缩放到一个固定的范围中, 使不同特征的权重更加平等, 降低模型过拟合风险, 提高模型的收敛速度。 使用均值中心化将每组数据的中心点都位于原点附近, 从而消除不同特征之间由于均值不同导致的平移差距。 原始光谱数据进行最大最小归一化和均值中心化后的数据如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 预处理数据透射光谱图Fig.2 Preprocessed transmission spectra

实验测得数据的光谱范围为181.1~1 002.4 nm, 具有很高的维度, 并且数据中不同信息对模型的影响存在差异, 有些信息对模型的影响较大, 能直接反映不同浓度下亚硝酸盐之间的差异, 但有些信息可能会对模型训练造成干扰, 影响预测性能。 因此在模型训练前应选择合适的方法对原始数据进行降维处理, 保留数据中的关键信息。

核主成分分析(kernel principal component analysis, KPCA)是一种常用的对高维数据进行降维的方法^[8]。 与传统的主成分分析将高维数据映射到低维线性子空间不同, 该方法是一种基于核技巧的主成分分析方法, 是将数据映射到更高维的特征空间中, 后通过求解该高维空间中的主成分来实现降维和特征提取的目的^[8]。 使用KPCA对预处理后的光谱数据进行降维, 图3为使用KPCA后两个主成分数据的二维分布图。 通过观察图3可知, 不同浓度的亚硝酸盐光谱数据区域划分明显, 表明KPCA对于本实验数据具有良好的效果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 主成分数据二维分布图Fig.3 Two-dimensional distribution of principal component data

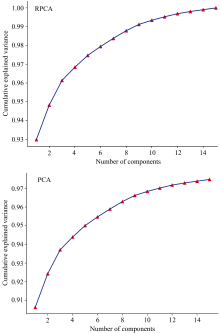
为了进一步探究使用KPCA操作的可行性, 将预处理过后的数据分别进行KPCA和PCA处理。 图4为分别进行KPCA和PCA操作后的主成分对原始数据的方差解释率, 通过图4对比可知, KPCA中3个主成分可以解释数据中96.1%的信息, 同时随着主成分个数的增加, 所能解释的数据比例也在增高, 当主成分数量为14时, 便能解释数据中99.99%的信息; 在PCA中3个主成分只能对数据中的92.53%信息进行解释, 当主成分个数为14时, 只能解释原始数据中的97.68%的信息。 即KPCA操作下更少的主成分可以代表更多的数据, 因此选择KPCA对光谱数据进行降维处理, 同时选择能代表原始数据97.94%信息的前六个主成分进行模型的训练。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 方差解释率曲线Fig.4 Variance explanation rate curve

粒子群算法(particle swarm optimization, PSO)是一种基于群体智能的优化算法, 其基本思想是通过模拟自然界中群体行为的方式来寻找最优解, 在粒子群算法中的每个粒子都代表一个解向量, 每个粒子的好坏根据适应度值进行判断, 并不断更新粒子的速度和位置, 使粒子能够向更优的解移动^[9]。 通过不断迭代更新, 最终找到全局最优解。 但由于该算法依赖粒子之间的信息传递和合作来找到最优解, 因此对于较为复杂的问题, 粒子群算法可能会受到束缚, 从而存在容易陷入局部最优解的缺点。

1.4.1 自适应学习因子和惯性权重

粒子群算法在对粒子进行更新迭代的过程中, 个体学习因子c₁、 社会学习因子c₂以及惯性权重ω 通常是固定的常数, 为了更好适应问题的非线性特点以及优化过程的动态变化过程, 引入自适应学习因子和惯性权重对PSO进行改进^[11]。 即每次根据当前粒子的适应度值和所有粒子的平均适应度值的大小对c₁、 c₂和ω 进行更新, 当粒子的适应度值比粒子种群中平均适应度值大时, 表明当前粒子距离全局最优解较远, 此时应更多的探索搜索空间, 故应增大c₁, 减小c₂和ω 的值从而增加算法的全局搜索能力; 当粒子的适应度值比粒子种群中平均适应度值小时, 表明当前粒子距离全局最优解较近, 应该利用历史的信息进行搜索, 故应减小c₁, 增大c₂和ω 的值从而加速算法的收敛速度。 式(2)、 式(3)、 式(4)分别为个体学习因子、 社会学习因子及惯性权重更新的方式。

w=ω-m1(ωmax-ωmin)fi-fminfmax-fminfifavg-1(2)

c1=c1+m2(c1max-c1min)fi-fminfmax-fminfifavg-1(3)

c2=c2-m3(c2max-c2min)fi-fminfmax-fminfifavg-1(4)

式(2)— 式(4)中, ω _max、 ω _min、 c_1max、 c_1min、 c_2max和c_2min分别表示惯性权重ω 、 个体学习因子c₁和社会学习因子c₂的最大值和最小值, f_i表示当前粒子的函数适应值, f_min表示粒子群体中最小的函数适应值, 相当于此时粒子群中的全局最优粒子, f_max表示粒子群体中最大的函数适应值, f_avg表示粒子群中的所有粒子的平均适应值, m₁、 m₂和m₃为0~1范围内的随机数。

1.4.2 粒子种群多样性引导策略(diversity guidance strategy)

自适应拓扑与探索丰富度(adaptive topology and exploration richness, ATER)多样性引导策略是一种用于增强粒子多样性和避免陷入局部最优解的策略。 该策略在每次迭代时都会计算粒子群多样性值, 该值的大小反映了整个粒子群中解的分布情况, 较高的多样性值表示种群分布比较均匀, 较低的多样性值表示种群分布集中在某个局部区域^[11]。 后根据粒子种群多样性值的大小来选择合适的速度更新方式, 该引导策略能够在保持种群多样性的同时, 增强粒子的全局搜索能力, 从而避免了粒子群陷入局部最优解。 粒子群X_n的多样性值是由种群中每个粒子与所有粒子平均位置的距离平均值来衡量的, 计算公式如式(5)所示:

D(Xn)=1Nd∑i=1N|xi, n-x-n|(5)

式(5)中, N为种群中的粒子个数, d为搜索空间的对角线长度, 代表搜索区域的大小, x-n为所有粒子的平均位置。

基于ATER策略的PSO算法速度更新规则为: 通过式(5)计算粒子群多样性值后, 当该值低于事前设定的多样性值下界d_low, 则代表当前种群多样性较低, 无法保证PSO算法的全局搜索能力, 因此切换到“ 排斥阶段” , 让种群中的粒子向着搜索区域的边界运动, 增大种群中的多样性值; 当该值大于事前设定的多样性值上界d_high, 则代表当前种群过于发散, 则切换到“ 吸引阶段” , 进而防止种群的粒子过于发散; 当该值在d_low和d_high之间时则切换到“ 中间阶段” , 在此阶段中的粒子受到自身的历史最优解吸引但被全局最优解排斥, 从而加强算法摆脱局部最优解的能力^[12]。 ATER策略下粒子速度更新规则如式(6)所示

Vid+1=ωVid+c1r1(Pbestid-xid)+ c2r2(Gbestd-xid)D(Xn)> dhighωVid+c1r1(Pbestid-xid)- c2r2(Gbestd-xid)otherwiseωVid-c1r1(Pbestid-xid)- c2r2(Gbestd-xid)D(Xn)< dlow)(6)

式(6)中, ω 位惯性权重, c₁、 c₂为个体学习因子和社会学习因子, r₁、 r₂为0~1范围内的随机数, Vid为粒子i在第d次迭代时的速度大小, xid为粒子i在第d次迭代时的位置大小, Pbes tid为粒子i在第d次迭代时的历史最佳位置, Gbest^d为第d次迭代时的全局最佳位置。

BP神经网络是一种基于人工神经网络的反向传播算法, 主要由输入层、 隐含层和输出层三部分组成, 用于训练多层前馈神经网络, 显著特点是输入样本信息正向传播, 输出误差信息反向传播, 并根据误差调整权重和偏置的值, 以提高模型的准确率, 当输出误差达到设定范围内或迭代次数达到设定值时算法结束。

学习率是神经网络算法中的一个重要的参数, 用于指定在反向传播过程中, 每次更新权重和偏置的调整步长大小。

学习率越大, 模型参数更新越快, 但可能会使模型不稳定; 学习率越小, 模型的参数更新越慢, 可能会导致训练的收敛速度过慢。

基于以上分析, 引入学习率自适应的神经网络算法, 利用sigmoid函数非线性的特点, 并结合损失函数的变化值, 使学习率自适应的增大或减小, 用来提高神经网络的性能和稳定性。 学习率自适应公式如式(7)、 式(8)所示

r=r(1.5-sigmoid(ft-ft-1))(7)

sigmoid=11+e-x(8)

式(7)和式(8)中, r为学习率, f_t-f_t-1表示t时刻与上一时刻损失函数的变化值。

根据式(7)可知, 当损失函数由大变小时, 表明模型性能有明显的提升, 学习率会自适应增大, 加快模型的收敛速度; 当损失函数变化较小时, 学习率以原步长速度收敛; 当损失函数由小变大时, 表明模型已接近局部最优解, 学习率会自适应减小, 让模型可以更加精确的收敛到最优解。

1.6.1 IPSO-BPNN模型

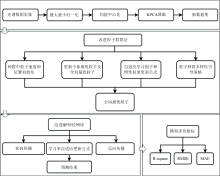
用IPSO-BPNN算法进行预测模型构建。 该预测模型的流程为: 使用IPSO算法在给定的搜索空间中寻找神经网络算法中权重和偏置的最优组合, 并将结果输出至BP神经网络模型中, 之后BP神经网络模型使用输出的最优组合进行预测模型的训练并输出预测结果的大小。

模型评价方面, 通过决定系数(R²)、 均方根误差(RMSE)和平均绝对误差(MAE)来评定模型的稳定与预测能力。 整个预测模型的流程图如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 模型流程图Fig.5 Model flow chart

1.6.2 粒子数和迭代次数的选择

使用IPSO算法寻找最优组合时, 需要选择合适的粒子数目和迭代次数。 图6为选择不同粒子数进行30次迭代的函数适应度值变化曲线, 从图中可以看出当迭代次数在25~30次时, 适应度值减小幅度很小, 说明算法已经收敛到了比较稳定的状态。 因此, 选择迭代30次便可满足本实验的需求。 同时, 粒子数目为70、 100和130时最终适应度值接近且比40个粒子的最终适应度值都要小, 为了算法的稳定性, 选择使用100个粒子进行30次迭代来对神经网络权重和偏置的最优组合进行寻找。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 适应度值对比Fig.6 Comparison of fitness values

将使用KPCA降维后能代表原始数据97.94%信息的主成分数据代入IPSO-BPNN模型进行训练, 模型的参数设置如表1所示。

表1

Table 1

表1(Table 1)

表1 IPSO-BPNN模型参数 Table 1 IPSO-BPNN model parameters ω max ω min c1max c1min c2max c2min r 0.9 0.4 1.5 0.4 1.5 0.4 0.1

表1 IPSO-BPNN模型参数 Table 1 IPSO-BPNN model parameters

其中, ω _max、 ω _min、 c_1max、 c_1min、 c_2max和c_2min分别为惯性权重、 个体学习因子和社会学习因子取值区间的最大值和最小值, r为神经网络中的初始学习率大小。

模型训练结果如图7所示, 预测模型的R²为0.984 360, RMSE为0.006 920, MAE为0.004 103, 说明IPSO-BPNN模型对于预测水体中亚硝酸盐的含量具有很好的效果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 模型预测结果Fig.7 Model prediction results

将构建的IPSO-BPNN模型同当前预测性能较好的随机森林(RF)模型、 线性回归(LR)模型、 粒子群优化算法下的支持向量回归(PSO-SVR)模型、 反向传播神经网络(BPNN)模型以及粒子群优化算法下的神经网络(PSO-BPNN)模型的R²、 RMSE和MAE三个参数作对比, 如表2所示。

表2

Table 2

表2(Table 2)

表2 模型预测性能对比 Table 2 Comparison of model prediction performance 模型 R2 RMSE MAE IPSO-BPNN 0.984 360 0.006 920 0.004 103 PSO-BPNN 0.964 756 0.011 136 0.006 289 PSO-SVR 0.940 512 0.013 257 0.010 031 BPNN 0.946 582 0.014 790 0.011 032 RF 0.951 038 0.012 896 0.005 913 LR 0.779 351 0.028 143 0.022 832

表2 模型预测性能对比 Table 2 Comparison of model prediction performance

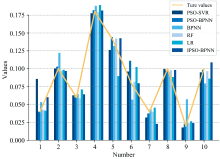
从上述模型的预测结果中随机抽取十个浓度的预测数据同真实值进行比较, 结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 模型预测结果比较Fig.8 Comparison of model prediction results

通过观察表2、 图8可知, 使用粒子群算法进行参数寻优后的BPNN模型比只使用BP-ANN模型进行浓度预测的性能有了显著的提升, 同时预测效果也优于其他模型, 说明在进行BP神经网络的训练前先进行参数寻优是可行的。 此外, 优化后粒子群算法的模型性能比未经优化的粒子群算法模型性能也有一定程度上的提升, 表明优化过后的粒子群算法可以更好地搜索参数空间, 找到更优的模型参数组合, 提高模型的拟合优度和预测精度。