引用本文
张文钧, 宋鹏, 鞠迎昕, 关婷予, 纪相彤, 韩朋. 双原子分子发射光谱分析Ar/Air/CH4等离子体射流转动温度研究 [J]. 光谱学与光谱分析, 2024,44(11): 3136-3141.
ZHANG Wen-jun, SONG Peng, JU Ying-xin, GUAN Ting-yu, JI Xiang-tong, HAN Peng. Study of the Rotation Temperature of Ar/Air/CH4 Plasma Jets by Diatomic Molecular Emission Spectroscopy [J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3136-3141.
Doi:10.3964/j.issn.1000-0593(2024)11-3136-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
双原子分子发射光谱分析Ar/Air/CH4等离子体射流转动温度研究
张文钧, 宋鹏*, 鞠迎昕, 关婷予, 纪相彤, 韩朋
大连民族大学机电工程学院, 辽宁 大连 116605
*通讯作者 e-mail: spony@dlnu.edu.cn

作者简介: 张文钧, 1996年生, 大连民族大学机电工程学院硕士研究生 e-mail: 674931799@qq.com

收稿日期: 2023-06-21 修回日期: 2023-12-13
基金: 国家自然科学基金青年科学基金项目(51409158, 51509035), 航空动力基金项目(6141B090540)资助
摘要

为了提升等离子体应用效果, 必须对等离子体的放电动力学过程进行深入探讨。 转动温度是反映等离子体放电过程中能量输运的重要参数之一, 目前主要采用波尔茨曼斜率法计算, 该方法常用于计算热力平衡状态下等离子体的转动温度, 在计算非热力平衡状态下的等离子体转动温度时误差较大。 针对这一问题, 提出了利用双原子分子谱带计算转动温度的分析方法, 采用针-环式电极等离子体射流装置进行试验, 向装置中通入Ar/Air/CH4混合气体放电形成等离子体射流, 工作电压为10~14 kV, 利用光谱仪采集不同放电电压下的等离子体射流的光谱数据用以计算转动温度。 选择OH(A—X)、 CH(A—X)以及N2+(B—X)发射光谱, 利用三种双原子分子波长区间内谱线不受振动温度变化所影响的特性, 对Ar/Air/CH4等离子体射流的转动温度进行研究。 在波尔茨曼斜率法计算得到转动温度±100 K范围内每20 K选取谱线, 与试验谱线进行拟合, 计算谱线拟合得到的均方根误差, 分析拟合准确度, 得到更为准确的介质阻挡放电(DBD)激励Ar/Air/CH4等离子射流的转动温度。 波尔茨曼斜率法计算出的转动温度在拟合时得到的均方根误差要高于最小均方根误差, 均方根误差能够减小38%。 利用OH、 CH、N2+谱带拟合得到最小均方根误差分别为4.6、 2.9、 2.1,N2+谱带拟合结果比OH谱带的拟合结果均方根误差减小61%。 结果表明, 在计算非热力平衡状态等离子体的转动温度时, 相比于波尔茨曼斜率法, 计算谱线拟合均方根误差的的方法能够有效地提升计算结果的准确度, 在进行谱线拟合时选择N2+(B—X)谱带的发射光谱与试验谱线进行拟合能够进一步提升计算结果的准确度。

关键词: 介质阻挡放电; 等离子体射流; 发射光谱; 转动温度
中图分类号:O53 文献标志码:A
Study of the Rotation Temperature of Ar/Air/CH4 Plasma Jets by Diatomic Molecular Emission Spectroscopy
ZHANG Wen-jun, SONG Peng*, JU Ying-xin, GUAN Ting-yu, JI Xiang-tong, HAN Peng
College of Mechanical and Electronic Engineering, Dalian Minzu University, Dalian 116605, China
*Corresponding author
Abstract

To enhance plasma applications' effect, plasma's discharge kinetic process must be explored in depth. The rotation temperature is one of the important parameters reflecting the energy transport in the plasma discharge process, which is mainly calculated by the Boltzmann slope method, which is commonly used to calculate the rotation temperature of the plasma in the thermodynamic equilibrium state and has a large error in calculating the rotation temperature of the plasma in the non-thermal equilibrium state. To address this problem, this thesis proposes an analytical method to calculate the rotation temperature using diatomic molecular spectral bands. A needle-ring electrode plasma jet device is used for the experiment, and a plasma jet is formed by discharging a mixture of Ar/Air/CH4 gas into the device with an operating voltage of 10~14 kV. A spectrometer collects the spectral data of the plasma jet at different discharge voltages to calculate the rotation temperature. The OH (A—X), CH (A—X) andN2+ (B—X) emission spectra were selected to investigate the rotation temperature of the Ar/Air/CH4 plasma jet, using the property that the spectral lines in the wavelength interval of the three diatomic molecules, are not affected by the change of vibration temperature. The rotation temperature of the DBD-excited Ar/Air/CH4 plasma jet was obtained by selecting one spectral line every 20 K in the range of ±100 K calculated by the Boltzmann slope method, fitting it to the experimental spectral line, calculating the root-mean-square error obtained from the fit of the spectral line, and analyzing the accuracy of the fit. The root-mean-square error of the rotation temperature, calculated by the Boltzmann slope method obtained in the fit, is higher than the minimum root-mean-square error, and the root-mean-square error can be reduced by 38%. The minimum root-mean-square errors obtained by fitting the OH, CH, andN2+ spectral bands were 4.6, 2.9, and 2.1, respectively, and the results of fitting theN2+ band were 61% lower than the results of fitting the OH band. The results show that calculating the root-mean-square error of spectral line fitting can effectively improve the accuracy of the calculation results, compared with the Boltzmann slope method when calculating the rotation temperature of the plasma in the non-thermal equilibrium state. The accuracy of the calculation results can be further improved by choosing the emission spectrum of theN2+ (B—X) band for fitting to the experimental spectral line.

Keyword: Dielectric barrier discharge; Plasma jet; Emission spectrum; Rotation temperature
引言

转动温度是反映等离子体放电过程中能量输运的重要参数之一[1]。 目前转动温度的测量方法主要采用自由基发射光谱温度测量技术, 通过光谱测量仪收集等离子体放电的光谱数据, 基于光谱数据采用波尔茨曼斜率法计算出转动温度和振动温度[2], 从而表征等离子体转动激发的强度和振动激发的强度。 随着计算机技术的进步与发展, 在基于分子光谱技术的计算程序、 软件及数据库方面, 出现了一些有代表性的成熟计算软件及数据库, 其中以NASA、 AMES研究中心的NEQAIR计算程序为典型代表, 该程序主要用来计算高温空气常见组分(如O2、 N2、 NO、 N2+)发射光谱的强度分布情况, 涉及到数十种分子、 原子、 离子, 以及数百万条的光谱谱线[3]。 21世纪初, SRI国际研究中心的Jorge Luque和David R Crosle开发的光谱计算模拟软件LIFBase软件, 提供了常见的10多种双原子自由基的模拟计算和光谱显示功能[4]。 Li等[5]提出了一种光学外差浓度调制光谱法, 通过将所有分配的谱线拟合到有效哈密顿量, 去除CS自由基旋转谱带的扰动。 Zheng等[6]提出了一种基于瑞利近似的多波长辐射测温方法计算温度和波长相关的发射率。 基于发射光谱诊断可以利用谱线拟合法计算转动和振动温度。

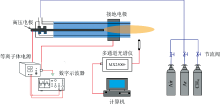
大气压常温等离子体射流是一种典型的非平衡状态等离子体。 本工作利用双原子分子OH、 N2+、 CH发射光谱, 对Ar/Air/CH4等离子体射流的转动温度进行了对比研究, 同时对比OH、 CH和 N2+三种自由基在谱线拟合时的均方根误差(root mean square error, RMSE), 均方根误差值越小说明试验谱线与模拟谱线更为接近, 拟合准确度越高; 确定均方根误差最小的谱线拟合波长范围, 同时对比波尔茨曼斜率法计算得到的转动温度值所对应的模拟谱线与最小均方根误差值校准后的谱线的均方根误差, 确认该方法的拟合准确性高于波尔茨曼斜率法, 转动温度的计算更加准确, 是一种适用于计算非热力平衡等离子体转动温度的方法, 有助于常温射流等离子的“ 温升效应” 的研究。

1 实验部分

图1为本试验的试验系统图。 放电装置为本课题组自主研制的等离子体射流激励器, 由环状铜片电极、 聚四氟乙烯绝缘介质管、 铜制中心电极和聚四氟乙烯进气管组成[7]。

图1 试验系统图Fig.1 Test system diagram

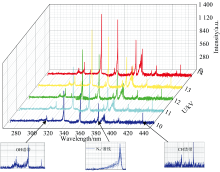
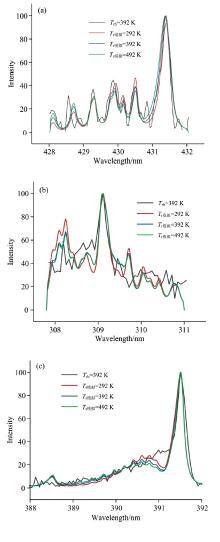
该试验系统由交流等离子体电源供电; 采用示波器测量放电电压及频率; 试验载气由瓶装高压Ar、 Air、 CH4提供, 气体掺混比为(Ar+Air)∶ CH4=20∶ 1, 三种气体经由气体管路通入后预混再通入试验器进行介质阻挡放电。 等离子体电源放电电压为10~14 kV, 放电频率为10 kHz; 光谱信息由多通道光谱仪海洋光学MX2500+采集, 光谱仪探头距离等离子体射流头部10 mm, 每一工况光谱信息均采集10次后取平均值。 图2为试验得到的等离子体射流特征谱线, OH基团光谱主要分布在306~315 nm, N2+基团光谱主要分布在386~395 nm, 甲烷脱氢后产生的CH基团光谱主要分布在430~435 nm[8]。

图2 DBD等离子体射流特征谱线Fig.2 Plasma jet characteristic spectral lines

2 波尔茨曼斜率法计算转动温度

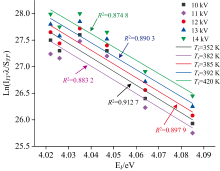
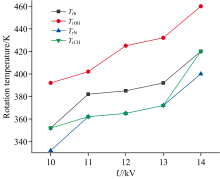
利用介质阻挡放电(dielectric barrier discharge, DBD)射流光谱数据通过波尔茨曼斜率法对转动温度进行计算, 见式(1)[9]; 得到电压为10~14 kV时等离子体的转动温度Trb分别为352、 382、 385、 392和420 K。 发现随着电压的升高转动温度也随之升高, 计算出的转动温度数值也和众多文献中的计算结果接近[10, 11, 12, 13], 拟合直线的R2(R-squared)值即相关系数在0.874 8~0.912 7之间(见图3), 整体大于0.85, 拟合精准度较高[14]。

lnIλ4SJ'J″=-EJ'kBTROT+C(1)

式(1)中, λ 为相应跃迁的波长; EJ'为转动跃迁(J'-J″)对应的上激发能, SJ'J″为霍尔-伦敦因子; J'、 J″为转动量子数, kB为波尔茨曼常数, T为转动温度。

图3 10~14 kV转动温度波尔茨曼拟合线Fig.3 Boltzmann fitting plot for 10~14 kV rotating temperature

3 谱线拟合及均方根误差计算
3.1 拟合区间选择

在分子确定的情况下, 霍尔-伦敦因子以及能级间的跃迁波数、 跃迁概率, 转动态和振动态的能量都为定值, 谱线强度只与各自由度温度相关, 当温度发生变化时, 谱线强度分布也发生变化[15]。 模拟光谱的谱线是利用Lifbase光谱数据库中的光谱数据与式(2)计算得出。

IV″J″V'J'=64π4PV″J″V'J'SJ″J'(VV″J″V'J')4c3N0g'eQvQe·exp-EvkTvexp-ErkTr(2)

式(2)中, IV″J″V'J'为谱线强度, PV″J″V'J'为跃迁概率, SJ″J'为霍尔-伦敦因子, VV″J″V'J'为能级间的跃迁波数N0为分子总数, g'e为电子简态并度, Qv为振动态的配分函数, Qe电子态的配分函数, Ev为振动态的能量, Er为转动态的能量, Tv为振动温度, Tr为转动温度, k为波尔茨曼常数。 为了解决波尔茨曼斜率法在计算非平衡等离子体误差过大问题, 提出了一种RMSE矫正拟合的方法减小计算误差。

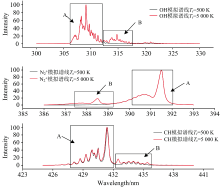
图4为由Lifbase得出振动温度变化时三个波长区间的模拟谱线图, 三个波长区间分别对应的OH(A— X)、 N2+(B— X)、 CH(A— X)三种自由基谱带, 当振动温度变化时三个波长范围内的A区域完全重合没有变化, B区域则发生了明显的变化。 根据此现象将不受振动温度影响的A区域作为谱线拟合区域从而得到等离子体的转动温度。 本工作中的模拟光谱数据都来自Lifbase软件, 该软件相对光谱强度都由归一法计算得出。

图4 振动温度变化时谱线变化Fig.4 Spectral line intensity vs vibration temperature

3.2 谱线拟合

将Trb输入软件得到相应的模拟谱线, 与分别在CH(A— X)、 OH(A— X)、 N2+(B— X)三个谱带所对应的波长区间与试验谱线进行拟合。 为了探究波尔茨曼斜率法计算转动度时的准确性, 在Trb± 100 K范围内, 每20 K选择一条温谱线进行拟合, 以电压为14 kV时三种双原子分子谱带的谱线拟合为例, 该条件下Trb=392 K, 拟合范围为292~492 K, 其中三条谱线拟合结果如图5所示, 之后通过比较谱线拟合均方根误差来确定转动温度的准确度。

图5 14 kV时不同转动温度下不同谱带谱线拟合图Fig.5 Spectral band fitting for different rotation temperatures at 14 kV

3.3 均方根误差计算

由于转动温度在小范围内变化时模拟谱线的变化较小, 无法确定拟合准确性, 而试验仪器与模拟计算参数精度不同导致谱线模拟的结果并非完全吻合, 因此通过计算试验谱线与模拟谱线均方根误差的方法来确定谱线拟合的准确性。 选取试验数据中5个极值点, 定义其峰值强度PE, i(i=1~5), 作为对比量分别求出不同转动温度Tr情况下自由基理论光谱数据对应的5个极值点的峰值强度PC, i(i=1~5), 均方根误差计算公式如式(3)

$\delta=\sqrt{\sum_{i=1}^{5} \frac{\left(P_{C, i}-P_{E, i}\right)^{2}}{5}}$(3)

将试验数据与不同转动温度下理论数据对应项计算分别求出各自的均方根误差δ 。 最后比较均方根误差最小者对应的转动温度即为试验光谱的转动温度, 电压为14 kV时CH(A— X)谱带谱线拟合时的拟合区域如图6所示, 计算得出的均方根误差值如表1所示。

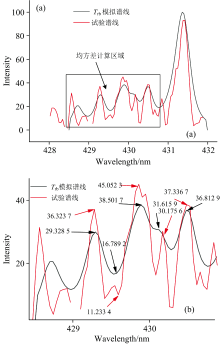图6 14 kV时Trb谱线拟合图及均方根误差计算区域Fig.6 Trb and TrCH spectral line fitting at 14 kV and RMSE calculation area

表1 14 kV时CH(A— X)谱带谱线拟合时得出的均方根误差值 Table 1 RMSE values obtained using fitting for the spectral line of the CH(A— X) band at 14 kV
4 结果与讨论
4.1 转动温度拟合结果

图7所示转动温度计算结果分别为波尔茨曼斜率法计算结果以及利用三种自由基谱带拟合后最小均方根误差值所对应的转动温度结果, 其中CH(A— X)谱带在谱线拟合时均方根误差值最小的转动温度定义为TrCH, 同理OH(A— X)和 N2+(B— X)谱带在谱线拟合时方差值最小的转动温度定义为TrOH和TrN。 波尔茨曼斜率法计算得出的结果与CH自由基、 N2+自由基的拟合结果较为接近, 而利用OH自由基得出的拟合结果与前三者有一定差距。

图7 10~14 kV时波尔茨曼斜率法与谱线拟合法转动温度计算结果Fig.7 Calculation results of rotation temperature by Boltzmann slope method and spectral line fitting method at 10~14 kV

4.2 拟合均方根误差对比

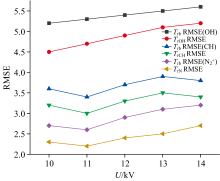
图8为波尔茨曼斜率法计算温度数值在不同波段的拟合均方根误差值为TrbRMSE(自由基)与该波段最小均方根误差值为Tr(自由基)RMSE对比, 在三个波段中计算得出的温度所拟合的均方根误差值均大于该波段的最小均方根误差值, 二者均方根误差在三个波段的最大差值分别为1.2、 0.9、 0.8这说明波尔茨曼斜率法在计算等离子体转动温度时误差可以利用谱线拟合法进一步优化, 得到更精确的转动温度, 均方根误差能够减小38%。

图8 10~14 kV时均方根误差计算结果Fig.8 Calculation results of root mean square error at 10~14 kV

对比三个波段的最小均方根误差值发现利用OH自由基波段拟合所得的最小均方根误差值为5.1左右, 明显大于CH自由基波段和 N2+自由基波段拟合得到的最小均方根误差值(分别为3.25左右和1.8左右), 说明利用OH自由基进行拟合得到的等离子体转动温度误差较大, 相比于OH谱带进行拟合, 利用 N2+谱带进行均方根误差能够减小61%左右。

5 结论

为了解决波尔茨曼斜率法在计算非热力平衡等离子体时误差较大, 计算结果无法验证的问题, 同时寻找拟合时准确度较高的双原子分子谱带, 利用OH(A— X)谱带、 CH(A— X)谱带以及 N2+(B— X)谱带中不受振动温度影响的波长区间对Ar/Air/CH4射流等离子体转动温度进行拟合, 计算拟合后的均方根误差, 结论如下:

(1)通过均方根误差校准后的谱线拟合得到的均方根误差, 明显小于波尔茨曼斜率法计算得到的转动温度在与试验谱线拟合时的均方根误差, 均方根误差能够减小38%。

(2)利用 N2+自由基波段拟合得到的最小均方根误差值小于OH自由基和CH自由基, 均方根误差能够减小61%, 因此利用 N2+(B— X)谱带进行谱线拟合能够进一步提高拟合的精确度。

参考文献
[1] Liu Z J, Xu H, Zhou C X, et al. Plasma Processes and Polymers, 2019, 16(11): 1970023. [本文引用:1]
[2] LI He-ping, YU Da-ren, SUN Wen-ting, et al(李和平, 于达仁, 孙文廷, 等). High Voltage Engineering(高电压技术), 2016, 42(12): 3697. [本文引用:1]
[3] Xia W J, Liu D X, Guo L, et al. Plasma Sources Science & Technology, 2019, 28(12): 47. [本文引用:1]
[4] Sun M, Chen W G, Zhang Y, et al. Plasma Science and Technology, 2011, 13(4): 470. [本文引用:1]
[5] Li C L, Deng L H, Zhang J, et al. Journal of Molecular Spectroscopy, 2013, (284-285): 29. [本文引用:1]
[6] Zheng S, Yang Y, Li X Y, et al. Fuel Processing Technology, 2020, 204: 106423. [本文引用:1]
[7] Wang B H, Chen L, Liu G M, et al. Physica Scripta, 2023, 98(4): 045612. [本文引用:1]
[8] PEI Huan, CHEN Lei, WANG Si-yuan, et al(裴欢, 陈雷, 王思远, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2022, 42(7): 2007. [本文引用:1]
[9] Liu Z J, Liu D X, Xu D H, et al. Journal of Physics D: Applied Physics, 2017, 50: 195203. [本文引用:1]
[10] Sainct F P, Durocher-Jean A, Gangwar R K, et al. Plasma, 2020, 3: 38. [本文引用:1]
[11] LIU Zhi-jie, CHEN Min, LIU Ding-xin (刘志杰, 陈旻, 刘定新). High Voltage Engineering(高电压技术), 2022, 48(10): 4196. [本文引用:1]
[12] LU Quan-fang, LI Juan-long, YU Jie, et al(陆泉芳, 李娟龙, 俞洁, 等). Journal of Analytical Science(分析科学学报), 2022, 38(2): 147. [本文引用:1]
[13] LIU Kun, XIANG Hong-fu, ZHOU Xiong-feng, et al(刘坤, 项红甫, 周雄峰, 等). Acta Physica Sinica(物理学报), 2023, 72(11): 222. [本文引用:1]
[14] Han Gookhee, Cho Guangsup. Applied Science and Convergence Technology, 2017, 26(6): 201. [本文引用:1]
[15] Moon S Y, Choe W. Spectrochimica Acta Part B, 2003, 58(2): 249. [本文引用:1]