引用本文
赵首博. 熵平均密度分段压缩感知反射光谱重建方法[J]. 光谱学与光谱分析, 2024,44(11): 3090-3094.
ZHAO Shou-bo. An Entropy Density Segment Compressed Sensing Method for Reflectance Spectrum Reconstruction[J]. Spectroscopy and Spectral Analysis, 2024,44(11): 3090-3094.
Doi:10.3964/j.issn.1000-0593(2024)11-3090-05  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
熵平均密度分段压缩感知反射光谱重建方法
赵首博1,2
1.广东海洋大学机械工程学院, 广东 湛江 524088
2.哈尔滨理工大学测控技术与通信工程学院, 黑龙江 哈尔滨 150080

作者简介: 赵首博, 1985年生, 广东海洋大学机械工程学院副教授 e-mail: shoubozh@126.com

收稿日期: 2023-06-07 修回日期: 2023-12-27
基金: 国家自然科学基金项目(61801148), 黑龙江省高校青年创新人才培养计划项目(UNPYSCT-2020187), 广东海洋大学科研启动经费资助项目(060302062301)资助
摘要

反射光谱作为物体表面重要特征被广泛用于远程遥感目标识别、 物质成分的含量检测、 农业作物成熟度检测、 医学影像的疾病诊断等领域。 为解决反射光谱数据冗余, 实现全光谱数据稀疏表达和提高光谱重建精度, 将压缩感知技术应用于光谱数据分析和处理。 针对全局光谱压缩感知重建方法中各波段数据稀疏度的差异性对采样率的限制条件不同, 提出熵平均密度分段压缩感知反射光谱重建方法。 首先定义熵平均密度作为光谱分段参考量来寻找光谱分段断点和判定各分段光谱的熵密度高低。 而后依据有限等距约束条件重新分配各分段光谱的采样率, 生成测量矩阵和稀疏矩阵完成各局部反射光谱稀疏感知。 采用正交匹配追踪算法求最优解, 分配各分段光谱的迭代次数, 用感知矩阵中的列原子和稀疏信号进行迭代匹配重构各局部反射光谱, 将各重构的局部反射光谱缝合为全局反射光谱。 用全局光谱压缩感知方法和该方法对标准色块24Munsell ColorChecker的反射光谱进行对比实验。 实验结果表明, 较之于全局光谱压缩感知方法, 该方法重建光谱曲线高熵密度区重建精度更高, 低熵密度区压缩效率更高, 在总压缩采样率不变的情况下, RMSE和MAPE统计数据得到改善, 提升了整体曲线重建效果。

关键词: 反射光谱函数; 压缩感知; 信息熵; 光谱分段
中图分类号:O433.4 文献标志码:A
An Entropy Density Segment Compressed Sensing Method for Reflectance Spectrum Reconstruction
ZHAO Shou-bo1,2
1. School of Mechanical Engineering, Guangdong Ocean University, Zhanjiang 524088, China
2. School of Measurement and Control Technology and Communication Engineering, Harbin University of Science and Technology, Harbin 150080, China
Abstract

Reflectance spectrum, as a significant characteristic of the object surface, is widely used in various fields such as remote sensing target identification, content detection of material components, agricultural crop maturity detection, and disease diagnosis in medical imaging. However, while the reflectance spectrum enriches target information, it also brings data redundancy, causing great difficulties in acquiring, processing, and transmitting spectral data. To settle these difficulties, our team has focused on spectral data analysis and processing utilizing compressed sensing technology. It was found that sparse representation of global spectral data was achieved, and spectral reconstruction accuracy was improved. Various sparsities of data in each spectral band constrain different sampling rates in spectral compressed sensing reconstruction methods. This paper proposes an entropy density segment compressed sensing method for reflectance spectrum reconstruction. Specifically, entropy average density is defined as the segmenting reference in the search for breakpoints. Based on the reference, the decision on whether the entropy density of each segmented spectrum is high or low can be given. After that, the sampling rates of each segmented spectrum are reassigned according to the limited equidistant constraint condition. The measurement and sparse matrices are generated for sparsity sensing of segmented reflectance spectrum. The optimal solution is obtained using the orthogonal matching pursuit algorithm. Iteration times of each segmented spectrum are reassigned. Each segmented reflectance spectrum is iteratively matched and reconstructed using the columns in the sensing matrix and sparse signals. Finally, the reconstructed segmented reflectance spectrums are stitched. A comparative experiment was conducted on the reflectance spectrum of the standard color block (24 Munsell ColorChecker) using the global spectral compressed sensing method and our proposed method. The experimental results show that compared with the global spectral compressed sensing method, the proposed method has higher reconstruction accuracy in high entropy density segments and higher compressed efficiency in low entropy density segments. RMSE and MAPE are improved under the same total compressed sampling rate, which enhances the overall curve reconstruction effect.

Keyword: Reflective spectrum function; Compressed sensing; Information entropy; Spectral segmentation
引言

反射光谱与目标表面的各光波段吸收、 透射相关, 取决于反射表面的材料、 微结构和纹理属性, 其在可见光范围内的视觉表现为目标颜色, 被广泛用于远程遥感目标识别、 物质成分的含量检测、 农业作物成熟度检测、 医学影像的疾病诊断等领域研究[1, 2, 3]。 然而反射光谱在丰富目标信息的同时带来了数据冗余, 给光谱数据的获取、 处理和传输造成很大困扰。 在色度学中采用传统的多项式法和伪逆法, 利用同色异谱现象实现色彩的近似表达, 但这类方法线性模型带来光谱密度畸变重建精度低, 样本数量决定色度复现质量的局限, 难以适用于色度学之外的其他领域。

压缩感知作为一种最优求解稀疏欠定采样系统的技术, 一经提出便受到信息领域学者关注[4, 5, 6]。 压缩感知是利用信号自身结构特征, 在远小于奈奎斯特采样定理要求的最小采样率下实现信号不失真的稀疏表达, 其这一特性恰能满足光谱数据获取、 处理和传输效率需求。 本课题组前期已成功将压缩感知应用于反射光谱分析和处理研究, 并发现全局光谱压缩感知重建中选用统一采样率不够完善[7, 8]。 在反射系数低的光波段, 可以进一步提高压缩比以减少数据冗余; 而在反射系数高的光波段, 需要降低压缩比以改善光谱重建质量。

基于此思路本文提出熵平均密度分段压缩感知反射光谱重建方法。 该方法将全局反射光谱基于信息熵平均密度分段, 通过判断不同子波段熵权重差异性分配稀疏采样率和最优重建算法迭代次数, 再将各子波段光谱分别局部压缩重建而后缝合为稀疏表达的全局光谱。 实验结果表明本方法能更高效率地压缩和高精度地重建反射光谱。

1 光谱熵密方法

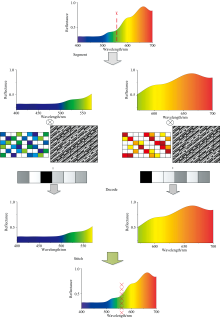
熵平均密度分段压缩感知(entropy density segment compressed sensing, EDSCS)光谱重建方法分为全局光谱熵密度分段、 局部光谱压缩感知和全局光谱重建三个模块, 如图1所示。

图1 分段压缩感知方法流程图Fig.1 Segmented compressive sensing flowchart

1.1 全局光谱熵密度分段

全局光谱熵密度分段引入了信息熵的概念并给出反射光谱分段的条件, 是本方法的先行基础和重要特色[9, 10, 11]。 信息熵是信息源概率分布不确定性的度量, 可用于评价反射光谱的信息量, 其计算公式为

H=-∑i=1n(pi·log2pi)(1)

式(1)中, pi为信息源不同取值对应的概率, i为信息源不同取值的序列号。 对于反射光谱, 不同光波长对应的反射概率为

pi(λ)=ri(λ)/∑i=1Nri(λ)(2)

式(2)中, ri(λ )为反射光谱密度, N由光波范围λ range=λ max-λ min和光谱采样间隔Ts确定

N=λrange/Ts(3)

定义熵平均密度作为光谱分段比较量

Denave=H/N(4)

各采样波长的熵密度Deni与Denave比较, 当

(Denbp-Denave)·(Denbp+1-Denave)< 0(5)

则此波长λ bp为光谱分段断点, 左右分割高低熵密度分布波段。

1.2 局部光谱压缩感知

为了改善对光谱数据的稀疏采样, 基于各分段光谱的熵密度高低配置相应压缩采样率。 各分段光谱的熵密度高低判定公式为

$\left\{\begin{array}{ll} \left(\operatorname{Den}_{b p}-\mathrm{Den}_{\mathrm{ave}}\right)＜0 & \rightarrow \text { 左低右高 } \\ \left(\operatorname{Den}_{b p}-\operatorname{Den}_{\mathrm{ave}}\right)>0 & \rightarrow \text { 左高右低 } \end{array}\right.$ (6)

设原全局反射光谱大概率满足有限等距约束条件(restricted isometry property, RIP)的压缩采样率为M/N, N为光谱数据量, M为稀疏测量次数。 以单断点两段局部反射光谱为例, 设左段熵密度低, 右端熵密度高, 各光谱数据量为N1和N2, N1+N2=N。 对于低熵密度局部反射光谱X1的K阶稀疏, 分配压缩采样率M1/N1,

M1=Klog(N1/K)(7)

对于高熵密度局部反射光谱X2, 分配压缩采样率为min[(M-M1)/N2, 1]。

对各局部反射光谱Xj稀疏感知, 获得测量值Yj为

Yj=ΦXj=ΦΨX'j=AX'j(8)

式(8)中, Φ 为测量矩阵, 根据分配采样率对原反射光谱信号Xj进行压缩采样, j=1, 2; Ψ 为稀疏矩阵, 将原局部反射光谱信号Xj稀疏化为Kj非零值的稀疏信号X'j; A为感知矩阵, 实现对局部反射光谱信号Xj的稀疏感知。

1.3 全局光谱重建

光谱重建是最优求解各局部反射光谱稀疏信号的过程

X-j=argmin‖X'j‖0　s.t.　Yj=AX'j(9)

用正交匹配追踪(orthogonal matching pursuit, OMP)算法求最优解, 感知矩阵中的列原子和稀疏信号进行迭代匹配, 每次迭代用最小二乘法计算残差值, 确保与当次更新列原子支撑集正交, 实现迭代结果的快速收敛[12, 13, 14]。

算法迭代次数L与支撑集需要的列原子数相关L≥ K, 对于低熵密度局部反射光谱, 算法迭代次数取L1=2K, 对于高熵密度局部反射光谱, 算法迭代次数取L2=(M-M1)L1/M1。

设低熵密度局部反射光谱第L1次迭代更新支撑集S1, 高熵密度局部反射光谱第L2次迭代更新支撑集S2, 重构的各局部反射光谱最优解为

X-j=(STjSj)-1STjYj(10)

缝合重构的局部反射光谱为全局反射光谱

r-=∑j=12DjX-j(11)

式(11)中, Dj为光谱缝合系数矩阵, 分别为

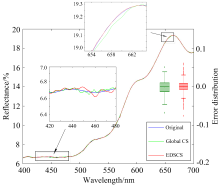
D1=10…001…0︙︙⋱︙00…100…0︙︙⋱00000N×N1　D2=00…0︙︙⋱000…010…001…0︙︙⋱00001N×N2

2 实验与结果讨论

实验验证提出的熵平均密度分段压缩感知光谱重建方法。 选用分光色度仪测量标准色块24Munsell ColorChecker的反射光谱作为原始数据, 光谱范围在400~700 nm, 光谱采样间隔1 nm, 每个色块301个光谱采样数据, 色块熵密度存在明显的高低分布范围, 适用于本方法分段研究。 为了直观说明本方法的优势, 对原反射光谱数据分别进行全局压缩感知(global compressed sensing, GCS)和熵平均密度分段压缩感知重建, 并与原数据比较。 图2为色块R1(茶褐色)的重建反射光谱曲线图, 蓝色曲线为原始数据, 绿色曲线为全局压缩感知重建结果, 红色曲线为熵平均密度分段压缩感知重建结果, 横坐标为光波长, 纵坐标为光谱反射率, 绿色箱型图表示GCS曲线与原曲线的误差分布, 红色箱型图表示EDSCS与原曲线的误差分布。 对色块R1熵平均密度分段有1个断点在572 nm处, 低熵密度区域压缩采样率为30%, 高熵密度区域压缩采样率为77%, 分别对高低熵密度区域局部放大观察重建效果可知, 在低熵密度区由于EDSCS方法的压缩采样率低重建误差较大, 在高熵密度区由于EDSCS方法的压缩采样率高重建误差较小。 因低熵密度区贡献权重低, EDSCS方法在与GCS方法的总压缩采样率不变50%的情况下, 提升了整体曲线重建效果。 从箱型图亦得到相同结论, 绿色箱型图的误差分布范围大于红色箱型图的误差分布范围, 而红色箱型图的奇异点比绿色箱型图的奇异点数量多, 集中出现在断点和低熵密度区。

图2 R1光谱重构曲线Fig.2 R1 spectral reconstruction curve

本方法可根据反射光谱熵密度分布进行多断点分段, 以色块R14(绿色)为例, 实验结果如图3所示。 色块R14熵平均密度分段有2个断点在483和593 nm两处, 低熵密度区域压缩采样率为40%, 高熵密度区域压缩采样率为67%, 总压缩采样率50%, 两边为低熵密度区域重建误差较大, 中段为高熵密度区域重建误差小。 箱型图说明, 与GCS方法相比, EDSCS方法的红色箱型图的误差分布范围小于GCS方法的绿色箱型图的误差分布范围, EDSCS方法有效提高了整体曲线重建精度。

图3 R14光谱重构曲线Fig.3 R14 spectral reconstruction curve

用均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为评价参数, 将EDSCS方法和GCS方法进行比较。 均方根误差通过统计测量数据偏离标准值的离散程度, 用于评价本方法重建精度, 其计算式为

$\text { RMSE }=\sqrt{\sum_{i=1}^{N}\left(r_{i}-\bar{r}_{i}\right)^{2} / N}$(12)

平均绝对百分比误差是大数据样本的相对误差度量指标, 可对不同测量尺度变化数据进行精度评价, 其计算式为

MAPE=100N∑i=1Nri-r-iri(13)

EDSCS方法和GCS方法的RMSE和MAPE计算结果, 如表1所示。 可见, 本EDSCS反射光谱重建方法在绝对精度和相对精度上都得到提高, 对各色块光谱处理都有很好的表现。

表1 GCS和EDSCS结果对比 Table 1 Comparison between GCS and EDSCS
3 结论

提出了熵平均密度分段压缩感知光谱重建方法, 依据光谱熵密度分布特点区分高低熵密度区块并重新分配各局部光谱的压缩采样率和重构迭代次数, 压缩感知重建各局部光谱并缝合成全局光谱。 此方法对不同光谱波段赋予了不同权重, 更为有效的针对不同贡献度光谱数据进行区别处理。 本文进行了EDSCS方法和GCS方法对比实验, 重建光谱曲线在高熵密度区更接近原始光谱曲线, RMSE和MAPE评价指标也证实本方法提高了光谱重建精度。

参考文献
[1] Zhou P, Sudduth K A, Veum K S, et al. Computers and Electronics in Agriculture, 2022, 196: 106845. [本文引用:1]
[2] Tomaniċ T, Rogelj L, Milaniċ M. Biomedical Optics Express, 2022, 13(2): 921. [本文引用:1]
[3] Tolmachev V A, Zharova Y A, Grudinkin S A. Optics and Spectroscopy, 2020, 128(12): 2002. [本文引用:1]
[4] Ghahremani M, Liu Y, Yuen P, et al. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 152: 34. [本文引用:1]
[5] Ye J C. BMC Biomedical Engineering, 2019, 1(1): 8. [本文引用:1]
[6] Zhao S, Yang Y. Scientific Reports, 2022, 12(1): 21054. [本文引用:1]
[7] ZHAO Shou-bo, LI Xiu-hong (赵首博, 李秀红). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(4): 1092. [本文引用:1]
[8] WANG Yang, YANG Meng-yu, ZHAO Shou-bo (王洋, 杨孟宇, 赵首博). Journal of Electronics & Information Technology(电子与信息学报), 2023, 45(7): 2605. [本文引用:1]
[9] Tsipouras M G. EURASIP Journal on Advances in Signal Processing, 2019, 2019(1): 10. [本文引用:1]
[10] Volyar A, Bretsko M, Akimova Y, et al. Optics Letters, 2019, 44(23): 5687. [本文引用:1]
[11] Omar Y M, Plapper P. Entropy, 2020, 22(12): 1417. [本文引用:1]
[12] Li Y, Zheng F, Xiong Q, et al. Measurement, 2021, 176: 109199. [本文引用:1]
[13] Zarei A, Asl B M. Computers in Biology and Medicine, 2021, 131: 104250. [本文引用:1]
[14] Qin Y, Zou J, Tang B, et al. IEEE Transactions on Industrial Informatics, 2020, 16(1): 215. [本文引用:1]