引用本文
管铖, 刘明月, 满卫东, 张永彬, 张清文, 方铧, 李想, 高汇锋. 连续小波结合随机森林算法估算互花米草叶片叶绿素含量[J]. 光谱学与光谱分析, 2024,44(10): 2993-3000.
GUAN Cheng, LIU Ming-yue, MAN Wei-dong, ZHANG Yong-bin, ZHANG Qing-wen, FANG Hua. Estimation of Chlorophyll Content in Spartina Alterniflora Leaves Based on Continous Wavelet Transformation and Random Forest Algorithm [J]. Spectroscopy and Spectral Analysis, 2024,44(10): 2993-3000.
Doi:10.3964/j.issn.1000-0593(2024)10-2993-08  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
连续小波结合随机森林算法估算互花米草叶片叶绿素含量
管铖1, 刘明月1,2,3,4,*, 满卫东1,2,3,4, 张永彬1, 张清文1, 方铧1, 李想1, 高汇锋1
1. 华北理工大学矿业工程学院, 河北 唐山 063210
2. 河北省矿区生态修复产业技术研究院, 河北 唐山 063210
3. 矿产资源绿色开发与生态修复协同创新中心, 河北 唐山 063210
4. 唐山市资源与环境遥感重点实验室, 河北 唐山 063210
*通讯作者 e-mail: liumy917@ncst.edu.cn

作者简介: 管 铖, 女, 1997年生, 华北理工大学矿业工程学院硕士研究生 e-mail: guancheng@stu.ncst.edu.cn

收稿日期: 2023-07-18 修回日期: 2023-12-22
基金: 国家自然科学基金项目(41901375, 42101393, 52274166), 河北省自然科学基金项目(D2019209322, D2022209005), 河北省高等学校科学技术研究项目青年拔尖人才项目(BJ2020058), 唐山市科技计划重点研发项目(22150221J)资助
摘要

叶绿素含量是检测植物生理状态的关键指标, 精准估算互花米草叶绿素含量对于表征其组分含量性状与量化其生理状态具有重要的意义。 以独流减河湿地互花米草实测高光谱反射率和叶绿素含量为数据源, 采用连续投影算法(sequential projection algorithm, SPA)对原始光谱及其数学变换和连续小波变换光谱进行特征提取, 基于随机森林回归(random forest regression, RFR)算法建立互花米草叶片叶绿素含量的高光谱估算模型。 结果表明: (1)连续小波分解低尺度下互花米草光谱时间分辨率更精确且频率更高, 对应的小波函数较窄, 可以更好区分光谱间差异, 突出特征光谱信息。 (2)除倒数(1/R)和对数的一阶微分[(logR)']外, 光谱数学变换与连续小波分解方法可有效反应光谱细节特征, 且小波分解效果总体上优于数学变换, 小波分解L10尺度与一阶微分(R')分别与叶绿素含量的相关性达到0.78和0.77。 (3)一阶微分(R')、 倒数的一阶微分[(1/R)']、 对数(logR)变换和连续小波分解可提升光谱对互花米草叶片叶绿素含量的估算能力, 其中基于一阶微分R'( R2=0.776, RMSE=0.510, RPD=1.893)和连续小波分解下L2、 L3与L4多尺度相结合构建的模型( R2=0.871, RMSE=0.305, RPD=3.846)分别为两种处理下的最优模型。 研究表明高光谱技术可以作为互花米草叶片叶绿素含量的无损检测手段, 连续小波分解后多尺度结合建立的高光谱估算模型可更加准确估算互花米草叶片叶绿素含量。

关键词: 互花米草; 叶绿素含量; 高光谱; 连续小波分解; 随机森林
中图分类号:X87 文献标志码:A
Estimation of Chlorophyll Content in Spartina Alterniflora Leaves Based on Continous Wavelet Transformation and Random Forest Algorithm
GUAN Cheng1, LIU Ming-yue1,2,3,4,*, MAN Wei-dong1,2,3,4, ZHANG Yong-bin1, ZHANG Qing-wen1, FANG Hua1
LI Xiang1, GAO Hui-feng11. College of Mining Engineering, North China University of Science and Technology, Tangshan 063210, China
2. Hebei Industrial Technology Institute of Mine Ecological Remediation, Tangshan 063210, China
3. Collaborative Innovation Center of Green Development and Ecological Restoration of Mineral Resources, Tangshan 063210, China
4. Tangshan Key Laboratory of Resources and Environmental Remote Sensing, Tangshan 063210, China
*Corresponding author
Abstract

Chlorophyll content is a key indicator of the physiological status of plants, and accurate estimation of chlorophyll content is important for characterizing its component content traits and quantifying its physiological status. In this paper, the hyperspectral reflectance and chlorophyll content (SPAD) of Spartina alterniflora in the Duliu-river wetland were used as the data source, the original spectrum was mathematically transformed and processed with continuous wavelet transformation (CWT). The spectral features were extracted using Sequential Projection Algorithm (SPA). And the hyperspectral estimation model of leaf chlorophyll content of Spartina alterniflora was developed based on random forest regression (RFR) algorithm. The results showed that: (1) CWT had more accurate time resolution and higher frequency in the low scale spectra, corresponding to a narrow wavelet function, which could better distinguish the differences between the spectra and highlight the characteristic spectral information. (2) Except for reciprocal and logarithmic first derivative spectrals, the spectral mathematical transform and CWT methods could effectively respond to the spectral detail features. CWT was generally better than the spectral mathematical transform, and the correlation between L10 scale and first derivative spectral reached 0.78 and 0.77. (3) First derivative spectral, reciprocal first derivative spectral, logarithmic derivative spectral and CWT could enhance the ability of spectral estimation of Spartina alterniflora chlorophyll content. The RF models based on first derivative spectral ( R2=0.776, RMSE=0.510, RPD=1.893) and CWT with the multiscale of L2, L3 and L4 ( R2=0.871, RMSE=0.305, RPD=3.846) were the optimal models. This study shows that hyperspectral techniques could be used as a non-destructive means of detecting chlorophyll content in leaves of Spartina alterniflora, and that the hyperspectral estimation model built by combining multiple scales after continuous wavelet decomposition could more estimate chlorophyll content in leaves of Spartina alterniflora.

Keyword: Spartina alterniflora; Chlorophyll content; Hyperspectral; Continuous wavelet decomposition; Random forest
引言

互花米草(Spartina alterniflora)是禾本科米草属多年生草本植物, 通常生长于河口和海岸的高潮带下部至低潮带上部, 具有根系发达、 耐盐耐淹、 繁殖力强、 种群扩散快和入侵力强等特性。 自20世纪70年代引入我国作为生态工程物种以来, 互花米草在我国沿海地区迅速蔓延, 截至2022年, 其入侵面积已达约6.8万公顷, 该物种已成为全球滨海湿地生态系统中最严重的入侵植物之一, 对我国沿海湿地生态系统产生多方面的影响[1]。 互花米草已经严重威胁湿地生态安全, 导致珍稀濒危鸟类数量和多样性急剧下降, 改变了线虫和大型底栖无脊椎动物群落的营养功能群结构, 对原生盐沼和海草床生态系统等造成了严重威胁[2]。 因此, 快速监测和评估互花米草的生长情况对于理解其种群动态和分布具有重要的实践意义。

叶绿素含量与植被的光合作用能力和初级生产力密切相关[3]。 准确测量叶绿素含量可以表征互花米草入侵的生长状况, 并且可以作为监测其入侵能力的重要指示。 传统叶绿素测定是通过丙酮、 乙醇混合液法破坏植被细胞膜, 再使用比色法或荧光法测定叶绿素含量。 然而, 这种方法会影响植被生理状态和生长, 叶绿素测定也容易受溶剂、 温度、 提取时间和溶解度等因素影响, 导致误差, 且实验操作繁琐费时[4]。 高光谱技术可获取地物连续反射曲线, 通过定量分析光谱特征, 可无损估测植物功能特性, 已成为研究植被生理生化特征与地表植被过程的强有力工具[5]。 Guo等研究烟草原始光谱732 nm处反射率与叶片叶绿素含量存在明显相关性[6]; 而植被高光谱数据在采集过程中受到外界环境、 湿度和仪器校准等因素影响, 导致反射光谱中存在干扰噪声。 Cheng等使用植被指数和0.2~2阶的分数导数处理苹果叶片高光谱数据, 发现当导数阶分别为0.2和0.4时, 利用支持向量机回归估测叶绿素含量和类胡萝卜素含量具有优势, R2分别为0.78和0.75[7]。 张雪茹等采用一阶微分、 倒数一阶微分等15种典型数学变换处理原始光谱, 精确地估测了冬小麦叶绿素含量[8]; 郭超凡等发现芦苇和香蒲叶片原始光谱反射率经包络线去除后虽一定程度上提高叶绿素估算模型的精度, 却难以有效去除白噪音[9]。

连续小波分解作为新兴的光谱处理方法, 可以有效地对光谱数据进行降噪和分解。 火龙果茎枝原始光谱反射率经数学变换和连续小波分解后, 对叶绿素含量的估测能力得到明显提升, 并且基于连续小波分解构建的模型具有较高的稳定性[10]。 目前, 用于植被叶绿素估算的线性模型有多元线性回归和多元逐步回归等[11, 12]。 多元线性回归适用于自变量少且相关性较小的情况。 然而对于互花米草光谱, 波段数较多且波段之间相关性强, 所以多元线性回归有一定的局限性[13]。 多元逐步回归可以筛除干扰变量, 选择合适的解释变量回归, 但是依然不能解决多变量间的共线性问题[14]。 Kang等研究表明机器学习是一种强大且具有高度自适应性的模式识别方法[15]。 Zhang等采用卷积神经网络和广义线性模型等机器学习模型建立白菜叶绿素含量估算模型, 广义线性模型验证集估算叶绿素含量的R2和RMSE分别为0.88和2.39[16]。 机器学习算法中的随机森林回归和支持向量机回归等具有极强的非线性拟合能力, 近年来被广泛应用于互花米草叶绿素的估算[17]。 随机森林回归由多棵决策树集成, 改善了单棵决策树的缺点, 更加稳定[18]。 冯海宽等利用随机森林回归、 支持向量机回归和神经网络法进行苹果叶片叶绿素含量估算, 结果表明随机森林算法估算叶绿素含量效果最优[19]。 王丽爱等利用随机森林回归算法构建小麦叶片每个生育期的SPAD值遥感反演多因子模型, 发现随机森林回归算法在3个生育期都表现出最强的学习能力[20]。

选择天津独流减河湿地为研究区, 利用实测互花米草叶片尺度高光谱反射率和叶绿素含量数据, 结合数学变换和连续小波分解与随机森林回归等方法, 构建互花米草叶片叶绿素含量的估算模型, 并分析模型效果优劣, 旨在为互花米草的入侵防治及管理提供依据。

1 实验部分
1.1 研究区概况

研究区位于天津市独流减河湿地, 该湿地属于暖温带半湿润季风性气候, 夏季炎热多雨, 冬季寒冷干燥。 潮汐类型属于半日潮。 由于水体热容量大, 湿地内气温有良好的调节作用, 因此独流减河湿地有利于亚洲东部候鸟在不同季节的迁徙过境和栖息繁殖[21]。

图1 研究区地理位置与采样点Fig.1 The location and sites of the study area

湿地采样点地理坐标为117° 35'E, 38° 46'N, 植被以芦苇(Phragmites australis)、 碱蓬(Suaeda salsa)、 柽柳(Tamarix chinensis)和互花米草为主。 2009年互花米草侵入天津独流减河河口, 近年来, 互花米草迅速繁殖扩散, 侵占芦苇和碱蓬等土著植物的生态位, 已成为独流减河湿地的优势植被物种。

1.2 数据采集

本研究于2021年10月20— 21日进行互花米草野外调查和样本采集。 依据全面性、 代表性和典型性的样地选取原则, 在天津独流减河湿地典型互花米草群落中随机设置均质样地, 内部布设0.5 m× 0.5 m的子样方, 随机选取各子样方内互花米草冠层上部、 中部和下部共9片绿色成熟叶片, 置于保温箱中带回实验室。 采用ASD公司生产的FieldSpec4获取叶片高光谱反射率, 测定范围为350~2500 nm, 光谱采样间隔在350~1 000 nm波段范围为1.4 nm, 1 000~2 500 nm波段范围为2 nm, 重采样间隔为1 nm。 每份样本重复测5条光谱曲线并使用光谱仪自带软件ViewSpec Pro取平均值作为该样本原始光谱信息。 为减少外界因素带入的误差, 每个样本光谱测定后进行白板校正。

采用CCM-200plus叶绿素测定仪获取叶片叶绿素含量, 根据朗伯比尔定律, 用660 nm处的吸光度减去940 nm处的吸光度, 得到的数值为该点叶绿素相对含量值[22]。 测量时避开叶脉, 测量位置与高光谱保持一致, 叶绿素含量均值作为该子样方互花米草叶片叶绿素含量, 共采集有效叶绿素含量样本83个。

1.3 光谱预处理

为消除光谱采集过程产生的噪声, 对平均光谱反射率进行S-G平滑得到互花米草原始光谱反射率R, 再对R做数学变换分解, 数学变换包括一阶微分(R')、 倒数(1/R)、 对数(logR)、 倒数的一阶微分(1/R)'、 对数的一阶微分(logR)'。 其中微分法能消除平行光谱噪声的影响, 重叠的光谱得到分离, 处理后的光谱分辨率更高、 更易找出特征波段[23]; 对原始光谱采用取倒数对数的方法, 也可以避免测量时屋内光线的亮度变化和叶片表面凹凸不平同样对实验结果的影响。

连续小波分解将原始光谱反射率分解成不同的振幅和尺度, 然后对微弱的光谱变化进行识别, 其在不同尺度和分辨率条件下可以提取和分析微弱的光谱反射率。 常见小波基函数有Bior、 Morlet、 Haar、 Gabor等, Biorthogonal 1.3小波基函数(Bior1.3)包含一个可逆小波滤波器和三个正交小波滤波器, 具有较窄的频率带宽, 更适用于分析高频光谱, 互花米草叶片特征信息被有效突出[24]。

对原始光谱反射率R进行多次小波变换实验, 其中以Bior1.3为基函数的小波变换结果较为理想, 故选取Bior1.3对进行21、 22、 23、 …、 210的连续小波分解, 即1— 10尺度分解(L1— L10), 研究中使用的公式

CWTfs, τ=1s∫-∞+∞ftΨ* t-τsdt(1)

式(1)中, CWTf(s, τ )表示连续小波变换后的结果, 其中s是尺度参数, τ 是平移参数, f(t)为互花米草原始光谱反射率, Ψ * (x)是小波的复共轭函数, 通常被称为小波基函数[25]。

1.4 特征波段选择

连续投影算法是一种矢量空间共线性最小化的前向变量选择方法, 本文使用Kennard-Stone样本迭代法, 特征光谱库中的样本数Ncal和波长数K可以组成一个光谱矩阵Xcal(Ncal× K), 记xk(o)和N分别为初始迭代向量和需要提取的波长个数, 对光谱矩阵列Xcal波段进行投影操作, 生成最大变量M=min(Ncal-1, K), 多次投影产生矩阵SEL(M× K), 经过计算投影波段、 最大投影波段指数迭代出候选波段组合。 每次迭代结束后, 分别对每一对xk(o)和N所决定的波长组合进行多元线性回归分析, 得到交叉验证均方根误差(RMSE), 选取RMSE最小的波长组合, 连续投影算法的优点是选择含有最少冗余信息及具有最小共线性的特征波段组合, 用以提高互花米草叶片叶绿素含量估算模型的预测能力和稳健性[26]。

1.5 随机森林回归建模

随机森林回归是由多个决策树集成的学习器, 具有良好的抗噪性能和极强的拟合能力, 可以高精度处理大数据集, 对于小数据样本建模效果也具有优势。 通过对多个决策树集成融合, 输出多棵决策树的平均值。 构建随机森林模型

h̅x=1T∑i=1Thx, θt(2)

式(2)中, h̅(x)为模型预测结果, {h(x, θ t ) }为基于x和θ t的输出, x为建模波段, θ t是独立同分布的随机向量, T为回归决策树的个数[27]。 随机森林回归模型通过R软件中“ randomForest” 包实现, 在建模过程中需要定义两个主要的参数: 每棵树的输入变量数量(mtry)和树的数量(ntree), 利用“ caret” 包的网格搜索法确定最优参数mtry和ntree, 其中mtry为1, ntree为500, 采用预测误差最小的参数组合进行最终建模。

1.6 模型精度验证

基于留一法(leave one out, LOO)交叉验证, 选取决定系数(R2)、 均方根误差(root mean squared error, RMSE)和相对分析误差(relative percent deviation, RPD)对所构建的互花米草叶片叶绿素含量估算模型进行精度评价。 其中, RMSE用来衡量观测值同真值之间的偏差, RPD相对分析误差是标准差与均方根误差的比值, 能更好地反映预测值误差的实际情况。 R2越大, RMSE越小, 建模精度越高, RPD越大, 模型越稳定[28]。 计算公式

$R^{2}=\frac{\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}$(3)

$\mathrm{RMSE}=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(\hat{y}_{i}-y_{i}\right)^{2}}$(4)

RPD=1n∑i=1n(yi-y̅)2RMSE(5)

式中, $\hat{y}$为第i个样本的预测值, yi为第i个样本的实测值, n为样本容量, y̅为所有样本实测值的平均值。

2 结果与讨论
2.1 叶绿素含量描述性分析

测量83个互花米草叶片叶绿素含量和光谱曲线, 叶绿素含量描述性统计列于表1。 由表1可知: 叶绿素含量SPAD数值范围为11.20~33.90, 平均值为21.01, 中位数为21.00, 标准差为4.90。

表1 互花米草叶片的叶绿素含量的统计性描述 Table 1 Statistic description of SPAD in Spartina alterniflora
2.2 叶片光谱特征

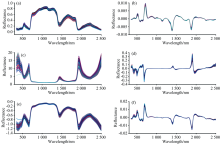
互花米草原始光谱与不同变换后光谱曲线如图2所示, 原始光谱曲线具有典型的健康植被光谱特征。 在可见光波段, 互花米草叶片光谱主要受叶绿素含量的影响, 390 nm蓝光波段和670 nm红光波段附近叶绿素吸收形成吸收谷, 在550 nm绿光波段附近吸收相对减少, 形成绿色反射峰。 互花米草叶片内部细胞组织受近红外波段强反射影响, 670~780 nm之“ 红边” 反射迅速增高。 近红外波段受叶片内部细胞结构和叶冠结构对光强烈反射的影响, 780~950 nm表现出高反射率特征, 叶片原始光谱反射率在1 107 nm处达到最大值0.88。 在近红外1 110~2 500 nm范围内, 互花米草叶片反射率整体呈现下降趋势。 受互花米草叶片含水量影响, 1 443和1 921 nm波段处光谱呈现明显吸收谷[29]。

图2 不同预处理方法后的反射光谱
(a): 原始光谱; (b): 一阶微分; (c): 倒数变换; (d): 倒数的一阶微分; (e): 对数变换; (f): 对数的一阶微分Fig.2 Reflectance spectra preprocessed by different methods
(a): Original spectra; (b): First derivative spectra; (c): Reciprocal; (d): First derivative of reciprocal; (e): Logarithmic transformation; (f): First derivative of logarithmic

原始光谱经数学变换后的高光谱特性明显改变, 局部光谱信息被有效凸显[图2(b— f)], 其中, 经一阶微分(R')、 倒数的一阶微分[(1/R)']、 对数的一阶微分[(logR)']变换, 波长668~2 500 nm间的光谱波长信息被突出。 一阶微分(R')可以在一定程度上减少大气、 光照等背景噪声和仪器因素带来的干扰, R中一些不明显的特征峰也被解析出来。 从图2(b— d、 f)可以看出, 经一阶微分(R')、 倒数(1/R)、 倒数的一阶微分[(1/R)']、 对数的一阶微分[(logR)']处理后的光谱, 消除了基线和背景的干扰; 图2(e)经对数(logR)变换, 波长550~1 930 nm附近光谱重合度变高, 减弱了散射对光谱的影响。

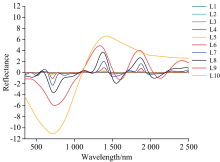
经连续小波分解处理后, 光谱高频反射率的微弱变化不断放大(图3)。 随着分解尺度增加, 互花米草光谱不断拉伸, 波峰与波谷特征也不断放大, 并且有一定的红移与蓝移现象, 其中尺度L1— L4对应的小波函数较窄, 表明小波函数扩展程度较小, 能够捕捉互花米草光谱中高频反射率的微弱变化。

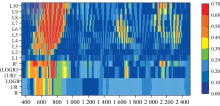
图3 连续小波分解光谱特性Fig.3 Spectral characteristics with continuous wavelet transform

2.3 叶绿素含量与不同变换光谱反射率的相关性分析

经数学变换和连续小波分解处理后, 变换光谱与互花米草叶片叶绿素含量相关系数有不同程度的提高(图4), 原始光谱R在可见光波段范围内与互花米草叶片叶绿素含量存在相关性, 两者之间的相关系数在564 nm处达到最大0.59; 一阶微分(R')、 倒数的一阶微分[(1/R)']、 对数的一阶微分[(logR)']、 倒数(1/R)、 对数(logR)与互花米草叶绿素含量相关系数分别在756 nm(R=0.77)、 755 nm(R=0.76)、 755 nm(R=0.76)、 558 nm(R=0.62)、 558 nm(R=0.62)处达到最大, 互花米草叶片光谱经数学变换后相关性明显提升, 其中一阶微分(R')、 倒数的一阶微分[(1/R)']和对数的一阶微分[(logR)']效果较为明显, 最大相关系数均达到0.75以上, 表明微分处理可以消除光谱背景噪声的干扰, 提高光谱分辨率和灵敏度, 凸显互花米草叶片光谱特征, 有利于筛选相关性较高的波段。 倒数(1/R)、 对数(logR)最大相关系数仅提升0.03; R经连续小波分解后, 除L1尺度外, 随着尺度的提高, 变换光谱与互花米草叶片叶绿素含量相关系数不断增加, 敏感波段多位于720 nm附近, 且敏感波段区间范围内有向长波方向移动趋势, 表明连续小波分解能放大互花米草叶片光谱局部光谱特征信息。 另外, 相对于R, 小波变换L4— L10分解尺度下, 1 625、 2 110与2 330 nm附近的叶绿素含量敏感性有所提升。 互花米草叶片光谱反射率与叶绿素含量在L10尺度, 712 nm处相关系数达到最大0.78。 表明连续小波分解更能有效提升互花米草叶片原始光谱反射率与叶绿素含量的相关性。

图4 不同光谱变换下的互花米草叶片光谱反射率与叶绿素含量敏感性分析图Fig.4 Sensitivity matrix of SPAD and spectral reflectivity under different spectral transformation methods

2.4 构建估算模型

以连续投影变换筛选出的特征波段为自变量, 互花米草叶片叶绿素含量为因变量进行随机森林回归, 分别构建数学变换和连续小波分解下的叶绿素含量预测模型(表2)。 互花米草光谱变量数过多, 其中包含对建模无效数据, 在预处理基础上使用连续投影算法对光谱进行冗余信息去除。 当提取特征波段数量为2个时, RMSE达到最小, 在超过2个特征波段时RMSE保持相对稳定, 挑选出对应的波段组合。 同理, 多尺度下L2、 L3和L4尺度相结合筛选RMSE最小值, 对应3列特征波段, 筛选的波段组合为708、 598和746 nm。

表2 基于数学和连续小波变换构建的互花米草叶片叶绿素含量估算模型 Table 2 The estimation model list of chlorophyll content in Spartina alterniflora leaves based on math transformation and continuous wavelet transform

基于数学变换构建的互花米草叶片叶绿素含量模型表明经过一阶微分(R')、 倒数的一阶微分[(1/R)']和对数(logR)处理建立的模型优于原始光谱, R2得到改善, 数值集中在0.45~0.78之间。 数学变换对随机森林回归模型效果影响较大, 其中一阶微分(R')变换建立的模型性能最好, R2为0.78, RMSE为0.51, 相比R, R2提升了0.35, RMSE降低了0.07, 可以较好预测互花米草叶片叶绿素含量。 原始光谱经过一阶微分(R')变换后互花米草叶片光谱反射率与叶绿素含量之间的关系转化为光谱反射率斜率与叶绿素含量间的关系, 消除了光谱反射率中的噪声。

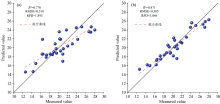
R经连续小波分解后, L1— L10尺度对应的R2和RMSE都得到改善, R2集中在0.44~0.85之间, 表明连续小波分析在信息降噪和挖掘特征信息方面优于传统光谱模型, 其中L2、 L3和L4尺度的R2达到0.80以上, 模型拟合能力较好。 低尺度下光谱时间分辨率更精确且频率较高, 高频光谱包含光谱细微变化, 可以更好区分光谱间差异, 突出特征光谱信息。 高光谱连续小波通过捕捉互花米草叶片不同频率范围内光谱变化趋势, 多尺度融合互花米草有效光谱, 综合考虑光谱的幅度、 相位和频率等信息, 更好去除光谱中高频噪声, 提高信噪比, 有助于提高互花米草叶片叶绿素含量模型的鲁棒性和泛化能力, 减少单一尺度对模型的干扰。 L2、 L3、 L4相结合建立的多尺度模型对特征波段变异性解释能力和模型预测能力更强, R2为0.87, RMSE为0.31, 相比R, R2提高了0.44, RMSE降低了0.27。 表明连续小波分解建立的互花米草高光谱估算模型可更加准确估算叶片叶绿素含量, 且多尺度比单尺度建模效果更具优势。 L2、 L3、 L4多尺度相结合预测的互花米草叶绿素含量与实测值的拟合曲线比一阶变换更接近1∶ 1线, 模型预测精度较高(如图5)。

图5 基于不同变换的叶绿素含量预测值散点图
(a): 一阶微分变换; (b): L2+L3+L4多尺度变换Fig.5 Scatter plots of predicted values of chlorophyll content based on different transformations
(a): First derivative spectral; (b): Continuous wavelet transformation with L2+L3+L4

3 结论

基于随机森林回归方法建立天津滨海新区独流减河湿地互花米草叶片叶绿素含量的高光谱预测模型, 重点讨论了不同光谱变换和连续小波分解建立叶绿素含量随机森林回归模型的估算效果, 明确了运用连续小波多尺度建模可以有效提升互花米草叶片叶绿素含量的估算精度, 具体结论如下:

(1)经连续小波分解处理后, 互花米草叶片光谱高频反射率的微弱变化不断放大。 低尺度下光谱时间分辨率更精确, 频率更高, 相应小波函数较窄, 能够捕捉互花草光谱的细微差异。 突出特征光谱信息。

(2)除倒数(1/R)和对数的一阶微分[(logR)']外, 光谱数学变换与连续小波分解可以有效消除光谱采集过程产生的噪音, 识别微弱光谱变化。 总体上, 小波分解效果优于数学变换。 小波分解L10尺度与一阶微分R'处理后光谱与叶绿素含量的相关性分别达到0.78和0.77。

(3)互花米草叶片高光谱经数学变换及连续小波分解发现, 一阶微分(R')、 倒数的一阶微分[(1/R)']、 对数(logR)变换和连续小波分解可提升光谱对互花米草叶片叶绿素含量的估算能力。 其中, 基于一阶微分的模型是数学变换中最优(R2=0.776, RMSE=0.510, RPD=1.893)。 连续小波L2、 L3和L4三种尺度相结合建立的估算模型(R2=0.871, RMSE=0.305, RPD=3.846), 是预测天津滨海独流减河互花米草叶片叶绿素含量的最优模型。

参考文献
[1] GENG Guo-biao(耿国彪). Green China(绿色中国), 2023, 4: 8. [本文引用:1]
[2] CHEN Pan, ZHANG Yan, ZHU Xiao-jing, et al(陈潘, 张燕, 朱晓静, 等). Acta Ecologica Sinica(生态学报), 2019, 39(7): 2282. [本文引用:1]
[3] YU Cai-fen, CHEN Peng-fei, LIU Chang-an, et al(于彩芬, 陈鹏飞, 刘长安, 等). Ocean Development and Management(海洋开发与管理), 2014, 31(8): 85. [本文引用:1]
[4] REN Hong, LUO Feng, XU Yan, et al(任红, 罗丰, 许彦, 等). Journal of Anhui Agricultural Sciences(安徽农业科学), 2014, 40(3): 1455. [本文引用:1]
[5] SHU Tian, LI Rui-jun, CHEN Zhi-hu, et al(舒田, 黎瑞君, 陈智虎, 等). Jiangsu Agricultural Sciences(江苏农业科学), 2023, 51(9): 222. [本文引用:1]
[6] Guo T, Tan C, Li Q, et al. Journal of Ambient Intelligence and Humanized Computing, 2019, 10: 3239. [本文引用:1]
[7] Cheng J, Yang G, Xu W, et al. Agronomy, 2022, 12(7): 1497. [本文引用:1]
[8] ZHANG Xue-ru, FENG Mei-chen, YANG Wu-de, et al(张雪茹, 冯美臣, 杨武德, 等). Chinese Journal of Eco-Agriculture(中国生态农业学报), 2017, 25(9): 1351. [本文引用:1]
[9] GUO Chao-fan, GUO Xiao-yu(郭超凡, 郭逍宇). Acta Ecologica Sinica(生态学报), 2016, 36(20): 6538. [本文引用:1]
[10] LI Li-jie, YUE Yan-bin, WANG Yan-cang, et al(李莉婕, 岳延滨, 王延仓, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(11): 3538. [本文引用:1]
[11] PEI Hao-jie, FENG Hai-kuan, LI Chang-chun, et al(裴浩杰, 冯海宽, 李长春, 等). Jiangsu Agricultural Sciences(江苏农业科学), 2018, 46(17): 224. [本文引用:1]
[12] JI Wei-shuai, CHEN Hong-yan, WANG Shu-ting, et al(纪伟帅, 陈红艳, 王淑婷, 等). Chinese Agricultural Science Bulletin(中国农学通报), 2021, 37(22): 143. [本文引用:1]
[13] Shen R, Zhang B W. MATEC Web of Conference, 2018, 176: 01033. [本文引用:1]
[14] Sharifzadeh M, Sikinioti-Lock A, Shah N. Renewable and Sustainable Energy Reviews, 2019, 108: 513. [本文引用:1]
[15] Meacham-Hensold K, Montes C M, Wu J, et al. Remote Sensing of Environment, 2019, 231: 111176. [本文引用:1]
[16] Zhang J, Zhang D, Cai Z, et al. Computers and Electronics in Agriculture, 2022, 195: 106814. [本文引用:1]
[17] ZUO Xue-yan, CUI Li-juan, LI Wei, et al(左雪燕, 崔丽娟, 李伟, 等). Acta Ecologica Sinica(生态学报), 2021, 41(15): 6159. [本文引用:1]
[18] Tzenios N. ResearchBerg Review of Science and Technology, 2020, 3(1): 94. [本文引用:1]
[19] FENG Hai-kuan, YANG Fu-qin, YANG Gui-jun, et al(冯海宽, 杨福芹, 杨贵军, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2018, 34(6): 182. [本文引用:1]
[20] WANG Li-ai, MA Chang, ZHOU Xu-dong, et al(王丽爱, 马昌, 周旭东, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2015, 46(1): 259. [本文引用:1]
[21] CHAI Zi-wen, LEI Wei-pan, MO Xun-qiang, et al(柴子文, 雷维蟠, 莫训强, 等). Wetland Science(湿地科学), 2020, 18(6): 667. [本文引用:1]
[22] ZHOU Xiao-sheng, ZHOU Yue-qin, PANG Lei, et al(周小生, 周月琴, 庞磊, 等). Journal of Anhui Agricultural University(安徽农业大学学报), 2012, 39(1): 150. [本文引用:1]
[23] Huang L, Li T, Ding C, et al. Sensors, 2020, 20(10): 2887. [本文引用:1]
[24] ZHAO Hai-long, GAN Shu, YUAN Xi-ping, et al(赵海龙, 甘淑, 袁希平, 等). Acta Optica Sinica(光学学报), 2022, 42(22): 209. [本文引用:1]
[25] TIAN Fu-ying, SUN Ying(田福英, 孙迎). Journal of Biomedical Engineering(生物医学工程学杂志), 2015, 32(3): 514. [本文引用:1]
[26] WAN Tao-lei, CHANG Jun-jie(万陶磊, 常俊杰). Nondestructive Testing(无损检测), 2019, 41(11): 43. [本文引用:1]
[27] SUN Xing-liang, HAO Xiao-hua, WANG Jian, et al(孙兴亮, 郝晓华, 王建, 等). Journal of Glaciology and Geocryology(冰川冻土), 2022, 44(1): 147. [本文引用:1]
[28] LI Zhen, WANG Jia-qiang, LI Zi-qin, et al(李贞, 王家强, 李紫琴, 等). Acta Agriculture Universitatis Jiangxiensis(江西农业大学学报), 2023, 45(5): 1273. [本文引用:1]
[29] LI Wen-ya(李文雅). Molecular Plant Breeding(分子植物育种), 2022, 20(24): 8586. [本文引用:1]