引用本文
李日浩, 马媛, 张伟峰. 基于多目标筛选堆叠回归的光谱反射率重建[J]. 光谱学与光谱分析, 2024,44(10): 2988-2992.
LI Ri-hao, MA Yuan, ZHANG Wei-feng. Spectral Reflectance Reconstruction Based on Multi-Target Screening Stacking Regression[J]. Spectroscopy and Spectral Analysis, 2024,44(10): 2988-2992.
Doi:10.3964/j.issn.1000-0593(2024)10-2988-05  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于多目标筛选堆叠回归的光谱反射率重建
李日浩, 马媛, 张伟峰*
华南农业大学数学与信息学院, 广东 广州 510642
*通讯作者 e-mail: zhangwf@scau.edu.cn

作者简介: 李日浩, 1999年生, 华南农业大学数学与信息学院硕士研究生 e-mail: 1459237319@qq.com

收稿日期: 2023-05-12 修回日期: 2024-01-09
基金: 国家自然科学基金项目(12271181, 61375006), 广州市自然科学基金项目(202201010426)资助
摘要

物体的光谱反射率完全决定了其物体色, 因此研究光谱反射率对于色彩信息要求较高的行业具有重大意义。 直接获取光谱反射率需要精密且昂贵的设备, 而通过建立模型, 由低成本的数码相机等设备获取的RGB响应值去预测光谱反射率, 可以大大降低成本。 基于回归方法的光谱反射率重建算法受到广泛关注, 其核心是建立RGB向量到光谱反射率向量间的映射关系。 对于大多数物体而言, 其表面的光谱反射率曲线具有平滑属性, 因此, 光谱反射率分量之间具有一定的相关性。 而已有的算法都是对光谱反射率向量每一个维度独立地建立预测模型, 没有将光谱反射率分量之间的相关性利用起来。 与传统的单输出回归方法不同, 多目标堆叠回归方法通过将首次预测输出值重新注入输入端来利用输出端之间的相关性。 基于多目标堆叠回归的光谱反射率重建取得了重要的进展; 然而, 传统的多目标堆叠回归方法存在着易受首次预测输出值误差影响的问题。 针对这一问题, 提出一种新的多目标堆叠方法, 对于首次预测输出值进行筛选, 从中选出误差较小的部分作为输入, 以此来保证下一步建立的模型精度。 该筛选方法可以在不知道真实值的情况下, 极大程度地保留误差较低的部分样本。 实验数据集来源为ICVL高光谱图像数据库, 评价指标为均方根误差与色度误差。 实验结果表明, 所提出的多目标筛选堆叠回归可以有效克服传统多目标堆叠回归所存在的问题, 做到比无堆叠时的误差更小, 说明提出的方法可以有效地利用光谱反射率分量之间的相关性。

关键词: 光谱反射率重建; 多目标堆叠回归; 筛选条件; 非线性拟合
中图分类号:TS801.3 文献标志码:A
Spectral Reflectance Reconstruction Based on Multi-Target Screening Stacking Regression
LI Ri-hao, MA Yuan, ZHANG Wei-feng*
School of Mathematics & Informatics, South China Agricultural University, Guangzhou 510642, China
*Corresponding author
Abstract

The spectral reflectance of an object completely determines its surface color; therefore, studying the spectral reflectance is of great significance for industries with high requirements for color information. Direct acquisition of spectral reflectance requires precise and expensive equipment. However, the cost of obtaining spectral reflectance can be greatly reduced by establishing a model that predicts spectral reflectance from RGB response values obtained from low-cost devices such as digital cameras. Spectral reflectance reconstruction algorithms based on regression methods have received widespread attention, and their core goal is to establish a mapping relationship between RGB vectors and spectral reflectance vectors. For most objects, the spectral reflectance curves of their surfaces have the property of smoothing. Therefore, there is a certain correlation between the spectral reflectance components. However, the existing algorithms have built prediction models for each dimension of the spectral reflectance vector separately, without taking advantage of the correlation between the spectral reflectance components. Unlike traditional single-output regression methods, the multi-target stacking regression method utilizes the correlation between outputs by reinjecting the first predicted output values into the inputs, and this paper studies spectral reflectance reconstruction based on multi-target stacking regression. However, the traditional multi-target stacking regression method is susceptible to the influence of errors in the first predicted output values. To address this problem, this paper proposes a screening method for the first predicted output value, selecting the part with less error as input to ensure the accuracy of the next model-building step. This screening method can preserve the samples with lower errors to a great extent, even without knowing the true values. The experimental data set in this paper is sourced from the ICVL hyperspectral image database, and the evaluation metrics are root mean square error and chromaticity error. The experimental results indicate that the proposed multi-target screening stacking regression can overcome the problems of multi-target stacking regression and achieve smaller errors than without stacking. Therefore, the proposed method in this paper can better utilize the correlation between spectral reflectance components.

Keyword: Spectral reflectance reconstruction; Multi-target stacking regression; Screening condition; Non-linear fitting
引言

在现代生产生活中, 人们对于色彩真实再现和管理的需求日益增加。 数码相机等通用色彩采集设备是在当时环境光照下获取物体的色彩信息, 信息中包含了环境光照和设备自身的因素, 并非物体颜色的本征参量, 这对于印刷出版[1]、 纺织服装[2]、 艺术品扫描存档[3]等对色彩要求较高的行业是一个重大挑战。 为了准确得到物体色, 需要获取物体表面的光谱反射率, 即物体表面在可见光波长范围内不同波长的反射光通量与入射光通量之比, 它是不受环境影响的本质物理属性。

直接获取光谱反射率数据需要使用专业的光学仪器, 如光谱仪和高光谱相机。 这些仪器的制造需要高精度的光学元件、 电子元件和机械元件以及复杂的校准和控制系统, 导致其成本较高, 并且灵敏度相对较低, 因此无法在实际应用中广泛使用[4]。 现如今, 人们普遍拥有可以获取高分辨率RGB响应值的低成本设备, 如相机、 扫描仪和手机等, 如果可以通过RGB响应值来重建光谱反射率, 光谱反射率的获取可以变得高效、 低成本和广泛使用。 因此, 如何建立一个准确高效的光谱反射率重建预测模型, 一直是光学研究领域的热点问题[5]。

目前, 相关科研人员已经提出许多从RGB响应值预测光谱反射率的方法, 其中基于回归的光谱反射率重建算法, 因其不需要任何关于成像系统和光照的先验信息而受到广泛关注[5, 6, 7]。 经典的基于回归的方法主要有核回归[8]、 支持向量机[9, 10]、 高斯过程回归[11]等。 核回归通过不同的核函数来处理数据, 使其可以灵活地获取光谱数据中的非线性关系[8]。 支持向量机主要的特点是它的解具有稀疏性, 可以减少噪声数据的影响, 保证预测模型的健壮性[9, 10]。 高斯过程回归通过贝叶斯模型推导出所需的高斯过程, 以此作为光谱反射率的后验分布, 并且能够给出预测值的不确定性[11]。

大多数物体表面的光谱反射率是一条光滑的曲线[12], 因此光谱反射率分量之间具有一定的相关性。 而已有的基于回归的方法都是分别建立从RGB响应值到光谱反射率每个分量的映射关系, 使得光谱反射率各个分量之间的预测相互独立, 没有利用到它们之间的相关性。 为了弥补这一缺点, 提出使用多目标堆叠回归方法来建立预测模型。 多目标堆叠回归的原理是通过将首次预测值与原输入值堆叠作为新输入端以充分利用输出分量间的相关性[13, 14, 15]。 本方法的目的是通过将初步预测的光谱反射率与RGB进行堆叠并作为新输入端的方式, 建立光谱反射率分量之间的联系, 从而利用它们之间的相关性来优化模型。 然而, 多目标堆叠回归方法存在着易受初步预测输出值误差的影响, 导致新的输入端准确度较低。 针对这一问题提出一种新的多目标筛选堆叠回归方法, 对初步预测输出值进行筛选, 从中选出准确度较高的部分与RGB进行堆叠, 以此来克服上述问题。 实验结果表明本文提出的多目标筛选堆叠回归方法的误差比无堆叠时更小, 并且模型精度比多目标堆叠回归更高, 可以更有效地利用光谱反射率分量之间的相关性。

1 光谱反射率重建原理

在数码相机成像过程中, RGB响应值的获取过程可以表示为

vi=∫λlλrλsiλdλ+ei, i=1, 2, 3(1)

式(1)中, vi为R, G, B其中的一个通道响应值, l(λ )为当前周围环境的照明光源的光谱能量分布函数, r(λ )为所成像物体的光谱反射率函数, si(λ )为第i个通道中相机设备的滤光片和感光片所构成的光谱敏感度函数, ei为第i个通道中数码相机成像时所产生的噪声, λ 为波长。 对于一般情况而言, 大部分物体的光谱反射率在400~700 nm之间的可见光波段中是平稳变化的, 在实际应用中可将其按10 nm的间距采样进行离散化, 因此, 式(1)可用矩阵的形式表示为

x=SLy+e(2)

式(2)中, x为3× 1的RGB响应值向量, S为3× 31的光敏感度矩阵, L为31× 31的光谱能量矩阵, e为3× 1的噪声向量。

令M=SL, 得到光谱响应矩阵M, 将其代入到式(2)中使其简化为

x=My+e(3)

光谱反射率重建的原理是求解式(3)的一个逆过程, 即通过已知的RGB响应值向量x求出光谱反射率向量y, 用式子表示为

y^=f(x)+e(4)

但这个过程是从3维的RGB响应值向量到31维光谱反射率向量的映射, 是一个典型的不适定问题。 由于计算过程中存在信息缺失, 所以设计重建算法的主要任务是如何开发和利用更多的先验信息, 使预测的光谱反射率更精确。

2 方法

假设拥有一组训练样本D={(x1, y1), (x2, y2), …, (xm, ym)}, 其中m为样本数, x为RGB响应值向量, y为光谱反射率向量, 可以构造一组回归函数yi=f(x), i=1, …, 31, 通过样本学习出输入x与输出y之间的对应关系, 以此预测未知的光谱反射率。

光谱反射率是一个高维度数据且空间分布结构复杂, 简单的线性回归方法难以拟合这样的数据, 而核回归不需要对数据分布做出任何假设, 可以灵活地适应各种数据类型和分布, 因此可以更好地处理光谱反射率数据[8]。 故以核回归方法作为基础的模型建立方式, 以此来展开实验。

2.1 核回归

可将光谱反射率重建问题表示为

$\min _{f \in H_{k}} H[f]=\sum_{i=1}^{m}\left(\boldsymbol{y}_{i}-f\left(\boldsymbol{x}_{i}\right)\right)^{2}+\gamma\|f\|_{K}^{2}$(5)

即找到一个映射关系f使得所有的样本预测出来的光谱反射率与真实的光谱反射率之间的误差达到最小, 其中m为样本的个数, γ 为常数, ‖ f ‖K2为正则化项[9]。

映射关系f采用核回归的方式, 可表示为

fx=∑i=1mciKxi, x(6)

对于c的确定可由式(7)求得

c=K+γI-1y(7)

式(7)中, I为单位矩阵, K为训练集中的输入端数据{xi }i=1m所得到的m× m格拉姆矩阵, 其表达式为

Kij=K(xi, xj)(8)

这里的核函数K(xi, xj)取最为广泛使用的高斯核函数, 其表达式为

Kxi, xj=exp-‖xi-xj‖22σ2(9)

式(9)中, σ 为该高斯核函数的带宽。 下述的实验部分中所提及到的训练方法均为高斯核回归。

2.2 多目标堆叠回归

多目标堆叠回归将初步预测的光谱反射率与RGB进行堆叠并作为新输入端, 在下一步建立预测模型时便可对光谱反射率分量之间建立映射关系。 该方法的核心思想是通过预测目标值之间的相关性来对初步的预测模型进行纠正, 从而提高预测模型的精度[13, 14]。

多目标堆叠回归方法分为两个阶段: 第一个阶段为通过训练样本D={(x1, y1), (x2, y2), …, (xm, ym)}训练出从3维的RGB向量x=(x1, x2, x3)到31维的光谱反射率向量y=(y1, y2, …, y31)的预测模型, 其中m为样本数, 从而通过RGB向量x得到光谱反射率向量的预测 y^; 第二阶段将第一阶段得到的 y^与x堆叠在一起, 形成新的训练样本D* ={(x1* , y1), (x2* , y2), …, (xm* , ym)}, 其中xl* =(xl, y^l), 通过新的训练样本D* 建立出新的预测模型, 从而得到新的预测值 y^^。

在上述过程中, 第一阶段所预测出来的 y^存在着一定的误差, 将会导致第二阶段中的输入端xl* 存在不准确性, 即会使得新的预测模型出现欠拟合问题。 因此, 我们需要对预测的 y^进行筛选, 提高新输入端的准确性。

2.3 筛选方法

2.3.1 拟合出系数矩阵

将光谱反射率视为一个自变量λ 在波长400~700 nm, 间隔为10 nm进行采样的离散函数, 共31个离散点。 将这31个离散点拟合成一个非线性函数

f(λ)=b3λ3+b2λ2+b1λ(10)

从而将高维度的光谱反射率转换为三维的系数矩阵B, 其中B=[b1b2b3], 如图1所示。

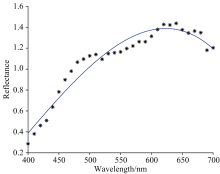图1 光谱反射率散点图与其拟合的非线性函数曲线图Fig.1 Scatter plot of spectral reflectance and nonlinear function fitting curve

值得注意的是, 这并非为降维处理, 而是从3维的角度去观测31维的光谱反射率, 每一个维度的数值大小都会影响到各个系数, 正如从二维的角度去观测三维的事物一样。

2.3.2 预测系数矩阵

训练一个预测系数矩阵模型, 将训练集中的光谱反射率真实值y转换为系数矩阵, 记为B0, 通过训练样本D0={(x1, B01), (x2, B02), …, (xm, B0m)}, 训练出从三维的RGB到三维的系数矩阵的预测模型, 该预测模型不会存在严重的维度灾难, 相对于直接预测光谱反射率而言, 精度会更高, 模型更为稳定。 因此, 所预测出来的系数矩阵会比预测出来的光谱反射率误差更低, 更接近真实值。

2.3.3 筛选

通过上述方法, 将预测出来的 y^转换为系数矩阵, 记为B1, 将直接预测出来的系数矩阵记为B2。 B1为从三维角度观测到的 y^, B2为更接近真实值的系数矩阵, 将这二者进行比较, 筛掉均方根误差大于均值的部分的预测值, 保留小于均值的部分的预测值, 留下的样本排列序号记录在b中。 通过该筛选方式, 能够在不知道真实值的情况下有效筛选出误差较小的部分的预测值, 从而可以提高多目标堆叠回归方法中第二阶段的输入端信息的准确性, 保证了模型的精度, 具体流程如图2所示。

图2 多目标筛选堆叠回归流程图Fig.2 Multi-objective screening stacked regression flow chart

3 实验结果与分析
3.1 数据集

ICVL(Interdisciplinary Computational Vision Lab)高光谱图像数据库[16]是由以色列贝尔谷大学的计算机科学系和电子工程系的研究人员共同开发的, 用于研究高光谱图像处理和分析的数据库, 其中的图片是从生活中的自然场景获取, 更为符合实际应用情况。 从该数据库中挑选出1张图片作为数据集来源, 编号为CC_40D_2_1103-0917, 该图像空间分辨率为1 392× 1 082个像素点, 光谱反射率为31个通道, 从400到700 nm, 间隔为10 nm, 相应的RGB响应椎则通过索尼3CCD相机获取[17], 其RGB图像如图3所示。

图3 高光谱图像的RGB渲染图Fig.3 RGB rendering of hyperspectral images

在上述图片中, 随机选取50× 40的方形区域, 共2 000个像素点, 即2 000个数据样本, 通过留M法将其划分为1 500个训练集样本与500个测试集样本。 其中留M法是一种交叉验证的方法, 具体过程为随机从数据集中选取m个样本作为测试集, 其余的样本作为训练集。

3.2 评价指标

评价指标为均方根误差RMSE与色度误差Δ Eab其表达式分别为

$\mathrm{RMSE}=\sqrt{\frac{\|\hat{\boldsymbol{y}}-\boldsymbol{y}\|^{2}}{31}}$(11)

ΔEab=(ΔL)2+(Δa)2+(Δb)2(12)

其中$\hat{y}$为预测的光谱反射率, y为真实的光谱反射率, 色度误差Δ Eab为将光谱反射率转换到CIELAB颜色空间中再对二者进行比较, L为亮度, a为颜色红到绿的过渡信息, b为绿到蓝的颜色过渡信息。

3.3 验证筛选方法的有效性

在筛选步骤中, 我们制定了不同的筛选条件去选取准确度高的预测样本, 并与真实值进行比较, 通过观察误差数据的结果来验证该筛选方法的有效性, 如表1所示, 其中u为B1与B2之间均方根误差的均值。

表1 不同筛选条件下的保留部分的均方根误差与色度误差 Table 1 Root mean square error and chromaticity error of the remaining samples under different screening conditions

由表1可得, 该筛选方法能够在无真实值的情况下, 有效甄别出误差较小的群体, 且筛选条件越严格误差越低, 具有一定的相关性。 但由于在训练第二阶段模型时需要一定的样本数量, 不适合制定太强的筛选条件, 因此, 选取小于均值的部分样本。

3.4 重建光谱反射率精度的比较

由表2可得, 直接使用多目标堆叠回归的模型比无堆叠的核回归精度要差, 而经过筛选后的堆叠回归方法可以使得模型精度更高。 因此, 本文所提出的多目标筛选堆叠回归能够有效降低多目标堆叠回归中第二阶段的训练样本的不准确性, 从而能够更加有效地利用光谱反射率分量之间的相关性。 图4和图5为随机抽取一组的不同方法重建光谱反射率曲线与误差波动曲线的比较。

表2 不同方法之间的重建精度比较 Table 2 Comparison of reconstruction accuracy among different methods

图4 不同方法重建的光谱反射率曲线的比较Fig.4 Comparison of spectral reflectance curves reconstructed by different methods

图5 不同方法重建的反射率误差波动曲线的比较Fig.5 Comparison of reflectance error fluctuation curves reconstructed by different methods

4 结论与展望

光谱反射率向量是一条光滑的曲线, 其各分量之间存在着一定的相关性, 利用这一特点能够提高重建算法的精度。 多目标堆叠回归通过将首次预测出来的目标值重新注入到输入端中, 从而利用各预测目标之间的相关性。 针对传统多目标堆叠回归算法易受首次预测值误差影响的问题, 提出了一种第二阶段训练样本筛选方法, 能够在不知道真实值的情况下有效甄别出误差较小的部分样本。 实验证明, 该方法能够有效筛选出误差较低的部分样本, 并且在筛选条件更严格的情况下, 筛选出的样本误差更小。 将该筛选方法运用于多目标堆叠回归中, 能够提高其第二阶段输入端的准确性, 优化了训练模型。 该筛选方法不仅可以用于光谱反射率重建, 还可以用于其他多目标且目标之间具有一定相关性的预测问题, 并且在将来可以作为一个约束条件, 将半监督学习法运用到重建光谱反射率问题。

参考文献
[1] Gonome H, Ishikawa Y, Kono T, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2017, 194: 17. [本文引用:1]
[2] Zhao H, Wang Y, Liu S, et al. Journal of Archaeological Science, 2019, 111: 105026. [本文引用:1]
[3] Gomez-Manzanares A, Vazquez Molini D, Alvarez Fernand ez-Balbuena A, et al. Sensors, 2022, 22(13): 4664. [本文引用:1]
[4] WANG Wen-ju, WANG Jiang-wei(王文举, 王江薇). Packaging Engineering(包装工程), 2020, 41(11): 254. [本文引用:1]
[5] Zhang J, Su R, Fu Q, et al. Scientific Reports, 2022, 12(1): 11905. [本文引用:2]
[6] LU De-jun, CUAN Kai-xuan, ZHANG Wei-feng(卢德俊, 爨凯旋, 张伟峰). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2018, 38(12): 3708. [本文引用:1]
[7] Lin Y T, Finlayson G D. Sensors, 2021, 21(16): 5586. [本文引用:1]
[8] Heikkinen V, Cámara C, Hirvonen T, et al. Journal of the Optical Society of America A, 2016, 33(6): 1095. [本文引用:3]
[9] Zhang W F, Dai D Q. Journal of the Optical Society of America A, 2008, 25(9): 2286. [本文引用:3]
[10] Rezaei I, Amirshahi S H, Mahbadi A A. Results in Optics, 2023, 11: 100405. [本文引用:2]
[11] Akhtar N, Mian A. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 42(1): 100. [本文引用:2]
[12] Trigt C V. Journal of the Optical Society of America A, 1990, 7(10): 1891. [本文引用:1]
[13] Tsoumakas G, Spyromitros-Xioufis E, Vrekou A, et al. ECML PKDD Proceedings, Part 111, 2014: 225. [本文引用:2]
[14] Borchani H, Varand o G, Bielza C, et al. Wiley Interdisciplinary Reviews: Data Mining & Knowledge Discovery, 2015, 5(5): 216. [本文引用:2]
[15] Spyromitros-Xioufis E, Tsoumakas G, Groves W, et al. Machine Learning, 2016, 104(1): 55. [本文引用:1]
[16] ICVL Hyperspectral Database. 2017. http://icvl.cs.bgu.ac.il/hyperspectral/. [本文引用:1]
[17] Cuan K X, Lu D J, Zhang W F. Optical and Quantum Electronics, 2019, 51(6): 175. [本文引用:1]