为了确保猕猴桃质量, 选择湖北省武汉市江夏区初阳奇异果园作为采摘地, 该果园种植了多种猕猴桃, 占地面积达到了350多亩。 选取其中的“ 云海一号” 猕猴桃为实验对象, 在果园里采摘。 选择标准为: 表面无病虫斑、 无新伤、 无疤痕, 完全套袋, 着色均匀, 单果重在90~110 g之间。 采摘完成之后经晾晒散去田间热, 转入冷库进行短期保存, 实验使用了280个猕猴桃果实。

采用ThermoFisher分子光谱部(Nicolet)推出的专业傅里叶变换近红外光谱系统Antaris-Ⅱ 采集猕猴桃的光谱数据。 Antaris-Ⅱ 系统主要由干涉仪、 光源、 激光器、 反射镜以及检测器等模块组成。 可以采集3 800~12 000 cm^-1(833~2 630 nm)范围内的光谱数据, 标准配置分辨率为4 cm^-1, 波数准确性为± 0.03 cm^-1, 10次测量的标准偏差小于0.006 cm^-1。

通过日本爱拓数字手持袖珍折射仪ATAGO PAL-α 测量猕猴桃样本的糖度, 其测量范围为0%~85%, 测量的精度为± 0.2%。 设备使用环境温度在10~40 ℃, 具有自动温度补偿功能, 可以通过温度传感器获取棱镜温度后进行温度补偿。

采集猕猴桃近红外光谱数据前, 先将Antaris红外分析仪预热15 min, 待光路系统稳定之后, 通过RESULT-Operation操作软件调整为积分球漫反射采样模式, 设置波数采集范围为4 000~10 000 cm^-1(1 000~2 500 nm)。 采集数据时, 将猕猴桃赤道部位的中心点作为光谱采集的点。 首先将每个猕猴桃果实平放在红外分析仪的光学台上, 然后移动猕猴桃调整位置, 确保赤道部位中心与红外分析仪的激光光源投射位置对齐。 之后使用专业软件进行光谱信息的采集, 并将数据实时传输到本地硬盘。

获取猕猴桃的近红外光谱后, 通过签字笔对光谱采集点进行标记。 随后使用专业工具挖出标记位置的果肉, 挤汁处理得到了果实汁液。 为了确定果汁的糖度含量, 采用了ATAGO折射仪进行测量。 测量前, 用蒸馏水清洁棱镜表面, 并按下“ ZERO” 键进行调零, 确保测量结果的准确性。 随后, 取适量的果实汁液滴在折光棱镜的镜面上测量。 当显示屏上的箭头闪烁三次后, 显示的数值即为测量的糖度值。 为了提高数据的准确性, 重复以上操作3次, 并将这三次的测量结果取平均值, 作为该采样点的糖度数据。 此外, 还以光谱采样点为基准, 在赤道部位顺时针120° 和逆时针120° 的位置进行了标记。 以相同的方式测量了这些标记点的糖度, 将以上三处标记点的糖度平均值作为整个果实的真实糖度。 然而实验记录显示这三点的糖度值基本一致, 因此也可将光谱采集点处的糖度值视为整个果实的糖度值。

为了确保原始样本服从同一分布, 使用基于蒙特卡洛随机采样结合T检验的奇异样本识别算法筛除异常值样本。 然后使用SPXY(sample set partitioning based on joint x-y distances, SPXY)样本划分方法对猕猴桃数据集进行划分, 通过这种划分方式能够增强模型的泛化能力。 为了减少数据采集过程中噪声等外界因素带来的干扰, 使用多元散射校正(multiple scattering correction, MSC)、 SG平滑滤波(Savitzky-Golay smoothing, SG)、 去趋势校正(de-trending, DT)、 矢量归一化(vector normalization, VN)、 标准正态变换(standard normal variable, SNV)五种方法对数据进行校正, 从中选择出效果最好的预处理方法。

由于仪器采集的波长信息较为丰富, 一条光谱数据包含了1 557个波长, 但并非所有的波长都含有有效信息, 从中选择与糖度变化相关的有效波长最为关键。 因此使用无信息变量消除法(uninformative variable elimination, UVE)、 竞争性自适应重加权算法(competitive adaptive reweighted sampling, CARS)和区间变量迭代空间收缩特征选择算法(interval variable iterative space shrinkage approach, iVISSA)进行特征波长选择, 然后使用连续投影算法(successive projections algorithm, SPA)对特征波长进行二次选择, 消除共线性波长。 最后选择效果最佳的波长选择方法, 降低数据维度。

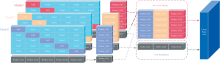
由于单一的回归模型易受数据分布的影响, 加上不同的模型解决问题的侧重点不同, 导致预测性能有一定的局限性。 为了避免上述缺陷, 研究人员开始尝试使用更多的模型来完成预测任务, 通过融合多个模型来获取更优越的预测效果。 目前常见的集成学习方法包括Bagging, Boosting以及Stacking等集成方法, 其中Stacking集成框架因其并行学习的优点而广受学者的青睐。 图1为Stacking集成学习的框架, 它由第一阶段的基学习器和第二阶段的元学习器组成。 通常会选择若干个不同类型的基学习器组成第一层模型, 训练集数据会在这层被平均分为若干份, 供基学习器进行交叉验证, 基学习器训练完之后对测试集进行预测。 第一层的预测结果通过组合形成新的特征集, 送入到第二阶段的元学习器进一步的训练。 在这一阶段, 元学习器结合基学习器新的特征, 修正第一层模型中的预测误差, 从而提升模型的预测性能。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 Stacking集成学习框架Fig.1 Stacking ensemble learning framework

Stacking集成学习算法的具体实现过程如下:

(1)划分数据集。 将猕猴桃的光谱数据采取SPXY法, 按照4∶ 1的比例来划分训练集D_train和测试集D_test, 并进行光谱预处理和特征波长选择。 设置五折交叉验证, 为此需要将训练集D_train平均划分为5份M={S₁, S₂, S₃, S₄, S₅}。 每次训练时取其中1份留做验证集S_i, 剩余的4份数据作为训练集供基学习器进行学习。 这样一个数据集可以训练5个模型, 对这5个模型的预测误差取平均就可以得到交叉验证的误差。

(2)选择基学习器并进行五折交叉验证。 每次选取n种基学习器进行组合, 每个基学习器通过五折交叉验证得到5个训练完成的模型, 并使用模型对验证集S_i和测试集D_test进行预测, 同时收集结果。 将模型得到的预测结果 S^i进行拼接, 得到 M^k={ S^1, S^2, S^3, S^4, S^5}, 把模型对测试集的预测结果取平均得到 D^k, 其中k表示是第k个基学习器。

(3)生成新的特征集。 将n个基学习器的预测结果进行合并, 得到新的训练集D'_train={ M^1, M^2, …, M^n}和新的测试集D'_test={ D^1, D^2, …, D^n}, 这将成为第二层预测模型的新数据集。

(4)训练元学习器。 由于第一层预测模型输出的特征和真实标签已经非常接近, 为了防止模型过拟合, 也为了缩短训练时间, 第二层选择简单的线性回归作为元学习器, 使用D'_train进行训练。 输入测试集D'_test获得最终的预测结果。

为了评价模型的预测性能, 比较不同模型之间的优劣, 采用训练集的决定系数 RC2、 训练集均方根误差RMSEC、 测试集的决定系数 RP2和测试集的均方根误差RMSEP评价模型的性能。 决定系数和均方根误差的计算公式如式(1)和式(2)所示

R2=1-∑i=1n(yi-y^i)2∑i=1n(yi-y̅)2(1)

RMSE=1n∑i=1n(yi-y^i)2(2)

其中n为样本总数, y_i为第i个猕猴桃的真实糖度, y^i为模型对第i个猕猴桃糖度的预测值, y̅为所有猕猴桃真实糖度的平均值。 决定系数R²值越接近1, 表示模型对数据的拟合度越高。 RMSE越接近0, 表示模型预测的糖度和真实值越接近。

由于测量环境和仪器设备等外界因素的影响, 采集到的猕猴桃近红外光谱信息可能会存在异常值。 这些异常的样本会影响原始样本数据的分布, 并且会对模型的训练以及预测产生影响, 因此采用蒙特卡洛结合T检验的方法筛选异常样本。

实验过程如图2所示, 首先随机筛选80%的光谱数据作为训练集, 剩余的20%作为预测集。 使用PLSR进行建模。 重复1 000次, 并记录每一次的预测均方根误差。 按照预测均方根误差从小到大进行排序, 统计前30%的模型中训练集样本出现的次数。 以80%的采样频率, 前300次PLSR建模的正常样本出现次数为240, 按照10%的标准进行上下浮动, 筛选出序号为0、 117、 166、 180、 188、 248和255样本的出现频次明显超出正常采样的频次, 表示这些样本会对模型的预测能力有较强的影响。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 蒙特卡洛交叉验证实验 (a): 各样本出现频次; (b): 各样本累计出现次数Fig.2 Monte Carlo cross validation experiment (a): Sample occurrence frequency; (b): Cumulative occurrences of samples

依次将上述检查出来的可疑样本从训练集中剔除, 然后利用PLSR建立预测模型。 使用新的测试集进行预测, 得到剔除每个可疑样本后新的预测均方根误差RMSEP。 同时为了进行对比, 在保留这些可疑样本的同时, 随机删除一个其他的样本进行建模预测, 重复100次后得到100个RMSEP。 将两者进行t检验判断是否来自同一分布, t检验所计算出的概率如表1所示。 以0.05的p值为评价指标, 117号样本与原始样本无显著性差异, 而0、 166、 180、 188、 248、 255号样本与原始样本有显著性差异, 被视为异常样本。 结合RMSEP指标, 可以认为117号样本是对模型有强影响的好样本。 而其他的样本有极低的概率出现在原始样本的分布中, 因此视作异常值排除。

表1

Table 1

表1(Table 1)

表1 各样本T检验结果 Table 1 T test results of samples 剔除样本 p值 剔除样本 p值 0 5.565× 10-16 188 2.2802× 10-11 117 0.087 9 248 6.070 4× 10-6 166 2.591 9× 10-9 255 0.000 8 180 2.407 7× 10-6

表1 各样本T检验结果 Table 1 T test results of samples

在剔除6个异常样本之后, 剩余274个正常样本供后续实验使用。 采取SPXY法, 按照4∶ 1的比例划分训练集和测试集, 得到219个训练集样本和55个测试集样本。 从表2中可以看出, 训练集的指标范围包括了测试集的范围, 这样划分出来的训练集的代表性较强, 训练出来的模型有更好的泛化能力。

表2

Table 2

表2(Table 2)

表2 训练集和测试集中可溶性固形物含量统计数据(° Brix) Table 2 Statistics of SSC in train set and test set(° Brix) 样本集 样本数量 最大值 最小值 平均值 标准差 训练集 219 17.77 11.23 14.26 1.31 测试集 55 16.7 11.9 14.15 1.13

表2 训练集和测试集中可溶性固形物含量统计数据(° Brix) Table 2 Statistics of SSC in train set and test set(° Brix)

为了削弱外界干扰因素对光谱的影响, 采用多元散射校正(multiple scattering correction, MSC)、 SG平滑滤波(Savitzky-Golay smoothing, SG)、 去趋势校正(de-trending, DT)、 矢量归一化(vector normalization, VN)、 标准正态变换(standard normal variable, SNV)五种预处理方法进行光谱预处理, 经过预处理之后的光谱如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同光谱预处理后的光谱对比 (a): 原始光谱; (b): 多元散射校正; (c): SG平滑; (d): 趋势校正; (e): 矢量归一化; (f): 标准正态变换Fig.3 Spectral data after different spectral preprocessing (a): RAW; (b): MSC; (c): SG; (d): DT; (e): VN; (f): SNV

与原始光谱相比, SG平滑滤波(SG)消除了光谱中的随机噪声, 光谱曲线更加平滑, 信号的信噪比得到了提高; 多元散射校正(MSC)和标准正态变换(SNV)将原始光谱曲线拉至均值, 以此来减小基线漂移对光谱产生的影响; 趋势校正(DT)则突出了曲线变化的趋势信息; 矢量归一化(VN)则是将每条光谱曲线当作矢量处理, 通过除以自身模长来得到同方向的单位矢量。 通过对原始光谱使用不同的预处理方式, 得到新的数据, 并将其送入PLSR模型进行全波长建模, 最后预测结果如表3所示。 可以看到去趋势校正(DT)的效果最差, 与原始光谱相比 RP2从0.680降到0.533, RMSEP从0.693上升到0.742。 但其他光谱预处理方法效果均比原始光谱的效果要好, 尤其是使用矢量归一化(VN)处理后的数据所训练的模型 RP2为0.720, RMSEP为0.618, 说明使用该预处理方法得到的数据最具有代表性, 模型能够得到更好的训练。 故选择矢量归一化(VN)作为光谱预处理方法。

表3

Table 3

表3(Table 3)

表3 不同预处理方法所建立的PLSR模型效果对比 Table 3 Results of PLSR models established by different preprocessing methods 预处理 方法 训练集 测试集 RC2 RMSEC RP2 RMSEP 无 0.853 0.492 0.680 0.693 MSC 0.741 0.682 0.707 0.652 SG 0.734 0.664 0.701 0.658 DT 0.955 0.282 0.533 0.702 VN 0.734 0.668 0.720 0.618 SNV 0.741 0.682 0.710 0.634

表3 不同预处理方法所建立的PLSR模型效果对比 Table 3 Results of PLSR models established by different preprocessing methods

2.3.1 无信息变量消除法

无信息变量消除法通过引入噪声, 通过交叉验证的逐一剔除法建模, 基于分析回归系数的算法逐渐消除信息量较少的波长, 最终达到特征提取的效果。 根据输入光谱波长数量, 将随机噪声维度设置为1 557, 确保每个波长都有对应的噪声维度。 通过范围寻优的实验将主因子数设为15。 留一法次数主要影响后续剔除单一波长后的回归实验次数。 如果次数设置过少, 实验结果可能会受到较大误差的影响; 相反, 次数过多则可能带来不必要的计算负担。 因此根据经验值将其设定为500次, 以在精确性和计算效率之间达到平衡。 随后通过光谱变量和随机噪声组成的自变量矩阵对糖度进行PLSR建模预测, 分析得到的回归系数向量, 计算稳定系数C。 选择随机噪声区域中绝对值最大的稳定系数C作为阈值, 从原始光谱中筛选稳定系数高于该阈值的波长作为特征波长, 最后得到了648个特征波长, 约占总波长的41.6%。

2.3.2 竞争性自适应重加权算法

竞争性自适应重加权算法(CARS)首先采用蒙特卡洛随机采样算法从训练集中选择数据作为建模集, 剩下的作为预测集, 使用PLSR进行建模回归。 每次选择回归系数较大的波长作为新的子集, 删除系数较小的波长, 经过多次建模之后得到预测均方根误差最小的模型, 其中剩余的波长即为选择出来的特征波长。 设置蒙特卡洛采样次数为50次, 使用五折交叉验证对模型进行评价。 图5(b)显示了交叉验证均方根误差随采样变量数的关系, 随着采样次数的增加, RMSECV呈现先减小后增大, 最后趋于稳定的形势。 在第17次采样时, 交叉验证集具有最小的RMSECV, 此时CARS筛选出了177个特征波长, 约占总波长的11.3%。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 UVE特征波长选择过程Fig.4 The process of UVE selecting characteristic wavelengths

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 CARS特征波长选择过程Fig.5 The process of CARS selecting characteristic wavelengths

2.3.3 区间变量迭代空间收缩特征选择算法

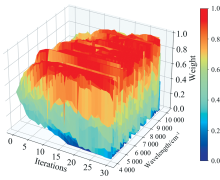
区间变量迭代空间收缩方法(iVISSA)是在VISSA算法的基础上提出的, 它结合了全局搜索和局部搜索的特点, 通过迭代的方式智能的实现波长间隔的选择。 参考文献[15]中的参数设置, 将二进制矩阵采样次数为500, 验证方式为五折交叉验证, 每个波长赋予0.5的初始权重。 在全局搜索的时候, 权重会随着迭代不断更新。 最后权重会趋向于0或者1这两个取值, 权重越大则表示越有可能是特征波长, 反之则意味着该波长将会被剔除。 从图6可以看到随着迭代次数的增加, 各个波长的权重趋向于两极分化, 最终权重为1的波长被选择为特征波长。 iVISSA算法筛选出了704个特征波长, 约占总波长的45.2%。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 iVISSA特征波长选择过程Fig.6 The process of iVISSA selecting characteristic wavelengths

2.3.4 二次筛选特征波长

为了进一步减少特征光谱的冗余信息, 降低模型的计算量。 在进行完上述三种特征波长选择之后, 对筛选出来的特征波长再次使用连续投影算法(SPA)来去除共线性。 SPA是一种前向的特征选择算法, 能够随着迭代不断剔除冗余信息, 有效的减少各个波长之间存在的共线性问题。 最终CARS-SPA筛选出了83个特征波长, 占总波长的5%; UVE-SPA筛选出了26个特征波长, 占总波长的1.67%; iVISSA-SPA筛选出了36个特征波长, 占总波长的2.31%。

2.3.5 基于特征波长的PLSR建模分析

对原始光谱进行矢量归一化处理, 通过不同的特征波长选择方法对光谱数据进行降维, 将转换后的光谱数据使用PLSR进行建模分析, 模型效果如表4所示。 可以看出原始光谱在经过特征波长选择之后, 模型的预测精度不降反增, 这是因为筛选出的特征波长能有效反应猕猴桃的可溶性固形物含量, 并且去除无关波长也降低了模型的计算量。 所以对光谱进行波长选择是很有必要的。 使用CARS方法提取的特征波长所建立的模型效果最好, 在测试集中的决定系数 RP2为0.805, 均方根误差RMSEP为0.498, 评价指标均优于其他的特征波长选择方式。 观察CARS模型在训练集上的评价指标, 可以推断出CARS所提取的特征波长更具有代表性, 能够被PLSR模型充分利用。 而CARS-SPA的预测精度相比于CARS有所下降, 这可能是在进行二次特征波长选择时筛掉了一些与猕猴桃糖度含量相关的特征光谱。 UVE方法对模型的预测效果有较明显的提升, 而iVISSA模型在筛除了一半的波长后, 所建立的PLSR模型预测精度仍与全波长模型持平。 UVE-SPA和iVISSA-SPA方法在删除共线性波长后, 模型的RMSEP得到了进一步的下降。 综合表4的评价指标, 确定CARS为最合适的特征波长选择方法。

表4

Table 4

表4(Table 4)

表4 基于不同特征波长选择方法建立的PLSR模型效果 Table 4 The results of the PLSR models based on different characteristic wavelengths selection methods 特征波长 选择方法 特征 波长数 训练集 测试集 RC2 RMSEC RP2 RMSEP 无 1 557 0.734 0.668 0.720 0.618 UVE 648 0.890 0.432 0.775 0.540 CARS 177 0.949 0.292 0.805 0.498 iVISSA 704 0.772 0.626 0.717 0.590 UVE-SPA 26 0.715 0.696 0.789 0.523 CARS-SPA 83 0.920 0.368 0.760 0.553 iVISSA-SPA 36 0.732 0.678 0.735 0.575

表4 基于不同特征波长选择方法建立的PLSR模型效果 Table 4 The results of the PLSR models based on different characteristic wavelengths selection methods

2.4.1 基学习器超参数设置

选择贝叶斯岭回归(Bayesian ridge regression, BRR)、 偏最小二乘回归(partial least squares regression, PLSR)、 支持向量回归(support vector regression, SVR)以及人工神经网络(artificial neural network, ANN)作为基学习器, 使用线性回归(linear regression, LR)作为第二层的回归模型。 其中BRR、 PLSR和SVR使用Sklearn实现, 使用Hyperopt的TPE方法对其中的超参数进行寻优。 ANN使用PyTorch深度学习框架搭建, 共有3个隐藏层, 神经元数量分别为: 100, 50, 20, 最后一层输出预测值。 使用CUDA对训练进行加速。 基学习器的一些关键超参数取值如表5所示。

表5

Table 5

表5(Table 5)

表5 基学习器部分关键参数 Table 5 Key parameters of the base learner 基学习器 超参数 取值 BRR alpha lambda 365.902 0.549 PLSR component 23 SVR Kernel C gamma RBF 3 020 555.176 12.258 ANN Batch Size Learning Rate epoch 64 0.01 5 000

表5 基学习器部分关键参数 Table 5 Key parameters of the base learner

2.4.2 基于Stacking集成学习的实验结果及分析

为了评估Stacking集成学习模型的效果, 对4种基学习器进行组合匹配, 产生了包括单一模型在内的15种组合方式, 建模效果如表6所示。

表6

Table 6

表6(Table 6)

表6 不同组合的模型效果 Table 6 The results of the models based on different combinations 建模算法 训练集 测试集 RC2 RMSEC RP2 RMSEP BRR 0.959 0.263 0.807 0.495 PLSR 0.949 0.292 0.805 0.498 SVR 0.825 0.546 0.827 0.466 ANN 0.804 0.560 0.795 0.511 BRR+PLSR 0.886 0.440 0.816 0.483 BRR+SVR 0.873 0.465 0.799 0.505 BRR+ANN 0.873 0.466 0.844 0.446 PLSR+SVR 0.880 0.451 0.809 0.492 PLSR+ANN 0.894 0.424 0.847 0.441 SVR+ANN 0.864 0.481 0.841 0.450 BRR+PLSR+SVR 0.889 0.435 0.811 0.491 BRR+PLSR+ANN 0.895 0.422 0.847 0.442 BRR+SVR+ANN 0.879 0.454 0.831 0.464 PLSR+SVR+ANN 0.893 0.425 0.853 0.433 BRR+PLSR+SVR+ANN 0.897 0.418 0.846 0.441

表6 不同组合的模型效果 Table 6 The results of the models based on different combinations

从表6中可以得出以下结论:

(1)以测试集的 RP2和RMSEP为主要评价指标, 预测性能最好的基学习器组合为PLSR+SVR+ANN, 测试集的决定系数 RP2达到了0.853, RMSEP为0.433。

(2)集成模型的性能与基学习器的组合有关。 以PLSR为例, 当其与个体性能最好的SVR进行组合时, 生成的Stacking模型预测精度甚至不如SVR单一模型; 而PLSR与个体性能一般的ANN进行组合时, 集成模型的预测性能得到了显著提升。 说明预测效果最佳的集成模型并非都由性能较好的基学习器组成, 集成模型的精度还与基学习器之间的差异性有关。 这点会在后面通过计算各基学习器之间的Pearson相关系数来进一步解释说明。

(3)大多数基学习器进行组合后的集成模型效果要比单一模型的准确率要高。 尤其是BRR、 PLSR与ANN结合以后, 模型的性能得到了显著提高, RP2平均上升了4%, RMSEP也有所下降。 随着基学习器种类的增多, 集成的优势越明显, 越来越多集成模型的性能超过了单一基学习器。 这说明Stacking集成学习框架能够利用不同模型的差异化特征, 进一步提升泛化能力。

(4)并非基学习器越多, 集成模型的性能就越好。 例如BRR+SVR的组合, RP2和RMSEP分别为0.799和0.505, 表现并不如单一的SVR模型。 预测性能最好的是PLSR+SVR+ANN的组合模型, 而不是BRR+PLSR+SVR+ANN, 这也说明了盲目的增加基学习器数量并不一定能提升集成模型的预测能力, 只有选择合适的基学习器才能带来性能的提升。

2.4.3 基学习器相关系数分析

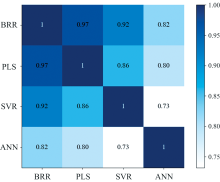
为了更好的分析Stacking集成学习算法的原理, 寻找各个基学习器的预测差异, 通过保存每个基学习器对测试集的预测值, 计算输出结果的Pearson相关系数。 计算公式如式(3)所示

r=∑i=1n(xi-x̅)(yi-y̅)∑i=1n(xi-x̅)2∑i=1n(yi-y̅)2(3)

式(3)中, x和y分别表示两个变量, n为样本总数, x̅和 y̅为变量的均值。 两个变量的协方差与各自标准差之商即为Pearson相关系数, 其值越大, 两者相关性越强, 反之则反。 各个模型所计算的相关系数如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 各基学习器相关系数矩阵Fig.7 Matrix of correlation coefficients of base learners

从相关系数矩阵可以看出各个模型之间均有0.7以上的相关系数, 属于较强的相关性, 这也是由于各个基学习器的学习能力较强所引起的。 对角线的相关系数为1, 这表示模型与自身的相关性最高。 BRR和PLSR的相关系数达到了0.97, 这是因为两者均属于线性回归模型, 而贝叶斯模型在估计的过程中引入了正则项, 相比于PLSR对数据利用得更加充分。 SVR和线性回归模型的相关系数也偏高, 但ANN与其他基学习器的相关性较低, 一方面是由于ANN属于深度学习, 训练方法和预测方式与其他模型不同; 另一方面是由于ANN本身对数据利用率不如其他模型, 训练集和预测集的准确率低于平均水平。 正因ANN与其他基学习器之间存在差异性, Stacking集成模型的性能才有显著的提高。 结合表6不同基学习器组合的预测表现可知, 在选择Stacking集成学习模型的基学习器时, 既要考虑单一模型的预测性能, 又要考虑模型之间的差异性, 选择合适的基学习器才能带来模型性能的提升。