基于连续小波变换和机器学习的小麦产量预测

引用本文

樊杰杰, 邱春霞, 樊意广, 陈日强, 刘杨, 边明博, 马彦鹏, 杨福芹, 冯海宽. 基于连续小波变换和机器学习的小麦产量预测[J]. 光谱学与光谱分析, 2024,44(10): 2890-2899.
FAN Jie-jie, QIU Chun-xia, FAN Yi-guang, CHEN Ri-qiang, LIU Yang, BIAN Ming-bo, MA Yan-peng, YANG Fu-qin, FENG Hai-kuan. Wheat Yield Prediction Based on Continuous Wavelet Transform and Machine Learning[J]. Spectroscopy and Spectral Analysis, 2024,44(10): 2890-2899.
Doi:10.3964/j.issn.1000-0593(2024)10-2890-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于连续小波变换和机器学习的小麦产量预测

樊杰杰^1,², 邱春霞¹, 樊意广², 陈日强², 刘杨², 边明博², 马彦鹏², 杨福芹⁴, 冯海宽^2,^3,^*

1. 西安科技大学测绘科学与技术学院, 陕西西安 710054

2. 农业农村部农业遥感机理与定量遥感重点实验室, 北京市农林科学院信息技术研究中心, 北京 100097

3. 南京农业大学国家信息农业工程技术中心, 江苏南京 210095

4. 河南工程学院土木工程学院, 河南郑州 451191

*通讯作者 e-mail: fenghaikuan123@163.com

作者简介: 樊杰杰, 1997年生, 西安科技大学测绘科学与技术学院及农业农村部农业遥感机理与定量遥感重点实验室, 北京市农林科学院信息技术研究中心硕士研究生 e-mail: fanjj74@163.com

收稿日期: 2024-04-02 修回日期: 2024-06-28

基金: 国家重点研发计划项目(2023YFD2000102, 2022YFD2001104), 河南省高等学校重点科研项目(24B420004), 河南省科技研发计划联合基金(应用攻关类)项目(222103810024), 河南省科技攻关项目(232102111115)资助

摘要

及时、准确的作物估产, 对作物管理决策和粮食安全评估具有重要意义。该研究在建立一种耦合连续小波变换(CWT)与机器学习准确预测小麦产量的方法。基于2020年—2021年两年小麦田间试验获取的开花期和灌浆期冠层高光谱数据及产量数据, 首先采用CWT提取三种小波特征(WFs), 分别为: 基于Bortua方法筛选的特征波段(Bortua-WFs)、提取WFs与小麦产量确定系数的前1%(1% R²-WFs)和单一分解尺度下的所有WFs(SS-WFs)。然后采用随机森林(RF)、 K最邻近(KNN)和极端梯度提升(XGBoost)三种机器学习算法构建产量预测模型。最后选取最优的光谱特征, 采用相同的方法进行建模并比较。结果表明: (1)三种WFs结合机器学习方法的模型均表现良好, 基于Bortua-WFs构建的模型具有更高的精度和稳定性。 (2)相比光谱特征模型, Bortua-WFs模型在各生育期的精度均有所提高, 开花期的 R²精度分别提高了17.5%、 4%和39.6%, 灌浆期分别提高了8.4%、 5.6%和16.9%。 (3)灌浆期的产量估算模型优于开花期, 结合Bortua-WFs和XGBoost的模型表现最佳, R²为0.83, RMSE为0.78 t·ha^-1。该研究比较了不同特征和方法相结合的性能, 确定了不同方案下的最佳模型精度, 为光谱准确预测小麦产量提供技术参考。

关键词: 连续小波变换; 高光谱; 机器学习; 小麦; 产量预测

中图分类号:S25 文献标志码:A

Wheat Yield Prediction Based on Continuous Wavelet Transform and Machine Learning

FAN Jie-jie^1,², QIU Chun-xia¹, FAN Yi-guang², CHEN Ri-qiang², LIU Yang², BIAN Ming-bo², MA Yan-peng², YANG Fu-qin⁴, FENG Hai-kuan^2,^3,^*

1. School of Surveying and Mapping Science and Technology, Xi'an University of Science and Technology, Xi'an 710054, China

2. Key Laboratory of Quantitative Remote Sensing in Agriculture of Ministry of Agriculture and Rural Affairs, Information Technology Research Center, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097, China

3. National Engineering and Technology Center for Information Agriculture, Nanjing Agricultural University, Nanjing 210095, China

4. College of Civil Engineering, Henan University of Engineering, Zhengzhou 451191, China

*Corresponding author

Abstract

Timely and accurate crop yield estimation is crucial for making informed decisions regarding crop management and assessing food security. This study aims to develop a method that combines continuous wavelet transform (CWT) with machine learning to predict wheat yield accurately. This research is based on the spectral data of canopy height and yield data obtained from two-year field trials conducted during wheat growth's flowering and filling stages in 2020—2021. Initially, CWT is employed to extract three wavelet features (WFs), namely Bortua-WFs based on the Bortua method, 1% R²-WFs representing WFs along with the top 1% determination coefficient for wheat yield, and SS-WFs encompassing all WFs under a single decomposition scale. Subsequently, three machine learning algorithms Random Forest (RF), K-nearest neighbor (KNN), and extreme gradient Lift (XGBoost) are utilized to construct the yield prediction model. Finally, optimal spectral features are selected using the same methodology for modeling and comparison purposes. The results demonstrate that: (1) all three WFs models combined with machine learning methods perform well, with higher accuracy and stability observed in the model built based on Boruta-WFs. (2) Compared to the spectral characteristic model, improved accuracy was achieved by utilizing Bortua-WFs at each growth stage; specifically, an increase in R² accuracy by 17.5%, 4%, and 39.6% during flowering stage, as well as an increase by 8.4%, 5.6%, and 16.9% during filling stage respectively were observed across different models.(3) The estimation model at the grouting stage outperformed that at the flowering stage; particularly noteworthy was the performance of XGBoost when combined with Bortua-WFs, which yielded an R² value of 0.83 accompanied by an RMSE value of 0.78 t·ha^-1. This study compared the performance of different characteristics and methods. It determined the best model accuracy under different schemes, which can provide technical references for the accurate wheat yield prediction by spectral technology.

Keyword: Continuous wavelet transform; Hyperspectral; Machine learning; Wheat; Yield forecast

文章图片

引言

粮食产量直接关系到国家粮食安全和人民生活水平^[1]。随着粮食需求量的不断增加, 粮食安全问题受到政府、企业和消费者的广泛关注。小麦作为世界主要粮食作物之一, 在中国有巨大的市场需求, 其生产状况直接影响到国家农产品的稳定性。在农业生产过程中, 对作物产量的准确预测至关重要, 有助于政府和生产者科学地制定粮食政策。

传统的产量预测方法需通过田间调查, 成本高、耗时、通量低, 易对作物造成破坏, 难以实现对大面积农田的快速和精确评估^[2]。近年来基于遥感技术的农作物估产逐渐成为一个研究热点^[3]。遥感技术可以非破坏性的方式提供大范围的高时空分辨率数据。随着遥感平台的多样化, 遥感技术已被认为是监测作物生长的有效方法^[4]。农业估产中常用的传感器包括高光谱、数码(RGB)、多光谱和热红外等^[5]。与其他传感器相比, 高光谱遥感技术可提供连续光谱信号, 进而探测作物冠层反射特征的细微变化, 越来越多地被用于作物生长监测和产量预测。肖璐洁^[6]等采用高光谱冠层反射率开发了多植被指数组合的小麦产量预测模型。崔怀洋^[7]等基于倒伏冬小麦的冠层反射率, 构建了“ 植被指数-千粒重-产量” 的模型, 较好地预测倒伏小麦的产量。 Liu^[8]等以高光谱植被指数为指标构建多元线性回归估产模型, 可为冬小麦产量估测提供快速、可靠的方法。传统回归方程的经验或统计模型, 如普通最小二乘(OLS)和多元线性回归(MLR), 在变量之间表现出很强的线性关系。然而它们无法预测非线性关系。机器学习(ML)算法借助大数据技术和高性能计算机的发展, 为数据解析带来了全新的途径^[9], 在作物估产中的应用越来越广泛。这些方法采用先进的统计技术模拟光谱信息和产量之间的复杂非线性函数。已建立的机器学习方法, 例如K最邻近(KNN)、随机森林(RF)、支持向量机(SVM)和极端梯度提升(XGBoost)等被用以建立产量预测模型, 实现更高的预测精度^[10]。有研究人员报告了机器学习算法预测方面的性能。如Li^[11]等使用6种机器学习和2种深度学习算法, 从多维特征预测作物产量。结果表明, XGBoost在产量预测方面优于五种机器学习模型(LR、 RF、 KNN、 ANN和SVR)和两种深度学习模型(LSTM和DNN), 具有较好的效果。 Abhasha Joshi^[12]等使用随机森林(RF)、支持向量机(SVM)、最小绝对收缩和选择算子(LASSO)和极端梯度提升(XGBoost)整合多个数据进行作物产量预测。结果表明, XGBoost的性能都比其他三种模型稍好。 XGBoost是一种基于决策树(DT)算法的梯度增强技术, 由于其速度、准确性和可扩展性而越来越受欢迎。众多研究表明, 应用高光谱遥感技术和机器学习算法进行作物产量预估可行, 能有效解决大范围农业生产中的挑战。

连续小波变换(CWT)是具有良好数学基础的信号处理工具, 能够充分利用冠层光谱各波段的丰富信息, 具有多重分析和时频局部优化的优点, 可以将信号分解为多个尺度上的小波系数, 从而提取出光谱信号中的微弱信息^[13]。在精准农业领域, CWT已被用于估算作物叶绿素含量^[14]和含水量^[15]等生理参数。而目前小麦产量预测模型大部分是基于光谱反射率或植被指数所构建, 采用CWT进行小麦产量预测的研究相对较少。 CWT在小麦产量预测模型中的性能有待进一步探索。

针对采用CWT进行小麦产量预测研究不足的问题, 本研究以小麦2个生育期的冠层高光谱反射率数据为数据源, 提取了3种类型的小波特征和光谱特征, 采用3种方法构建各生育期的估产模型, 探究小波特征对小麦产量预测的影响, 以期对小麦产量的产前预测提供重要的参考信息。本研究的具体目标包括: (1)探究CWT用于冬小麦产量预测的潜力; (2)评估不同类型WFs小麦产量预测模型的性能, 确定最佳WFs; (3)构建CWT和机器学习结合的最优小麦估产模型。

1 实验部分

1.1 试验设计

2020年— 2021年在中国北京市昌平区的小汤山国家精准农业研究中心(40.17° N, 116.43° E)开展冬小麦长期定位观测试验, 研究区平均海拔36 m, 属暖温带大陆性半湿润半干旱季风气候。研究区为试验田, 共32块小麦地块, 东西总长80 m, 南北总长60 m, 每块小区面积为15 m× 9 m。 2020年采用试验品种为京东18号, 2021采用试验品种2个: 中麦1062和京花11。两年试验均设4个氮素水平: 0 kg尿素· 亩^-1(N0)、 13 kg尿素· 亩^-1(N1)、 26 kg尿素· 亩^-1(N2, 正常处理)、 39 kg尿素· 亩^-1(N3); 设4次重复, 总计8次相同处理组合, 如图1所示。于开花期(2020.5.14, 2021.5.11)和灌浆期(2020.6.1, 2021.5.26)进行田间获取小麦冠层光谱数据, 产量数据于收获期获取, 共计获取64个产量数据。

	Figure Option View Download New Window
	图1 研究区位置示意图Fig.1 Location diagram of the research area

1.2 光谱数据采集与预处理

在开花期和灌浆期使用ASD公司FieldSpec4产品采集小麦冠层高光谱数据, 仪器采集的波长范围为350~2 500 nm, 重采样间隔为1 nm, 包含2 151个波段。每次测量于当地时间10:00— 14:00的窗口期间, 将传感器垂直放置在作物冠层上方60 cm处, 在每个小区地块内进行10次光谱测量, 采用全部数据的平均值作为最终结果, 每采集4个小区后采用标准白色参考板进行校准。

完成数据采集后, 使用ViewSpecPro软件对原始数据处理, 并检查数据的正确性并剔除异常数据, 最后生成反射率文件。采集到的地物光谱曲线还存在一定的噪声, 本研究采用CWT可以有效的去噪和分解。参照已有研究成果, 作物生长状态可以通过其可见光和近红外区域的光谱特性评估^[16]。本研究在450~950 nm之间的冠层光谱数据进行后续研究。

1.3 小麦产量测定

收获前, 对每个冬小麦小区进行了产量测定, 采用点抽样法获取了1 m× 1 m的籽粒样本。为避免边缘效应, 确保每个采样点距离农田边缘至少2 m。谷物脱粒和风干后, 测定其重量和含水量, 以含水率为14%时计算各样点产量。使用14%含水率作为小麦测产的标准, 有助于确保小麦品质、安全贮藏和简化计算过程, 产量计算如式(1)所示。

$\begin{array}{l} 实测产量 = 取样鲜麦重 \times [1 - 籽粒含水量] \div \\ [1 - 14 %] \div 取样面积 \end{array}$ (1)

1.4 特征提取与分析

1.4.1 光谱特征

光谱指数(vegetation indices, VIs)是通过将不同波段的反射率进行代数组合而得到的一种参数, 能够减少条件背景对光谱反射率数据的干扰, 比单波段具有更高的灵敏性。本研究在前人研究的基础上, 选择17个和产量相关性较好的高光谱指数。表1为本研究植被指数的定义、描述和来源。

表1 本研究中的植被指数 Table 1 Vegetation indices

定义		公式	来源
NDVI	normalized difference vegetation index	(R₈₀₂-R₆₈₂)/(R₈₀₂+R₆₈₂)	[17]
GNDVI	green normalized difference vegetationindex	(R₈₀₂-R₅₆₂)/(R₈₀₂+R₅₆₂)	[17]
PRI	photochemical reflectance index	(R₅₇₀-R₅₃₀)/(R₅₇₀+R₅₃₀)	[18]
CARI	chlorophyll absorption reflectance index	(R₇₀₂-R₆₇₀)-0.2(R₇₀₂+R₆₇₀)
MSR	modified simple ratio	(R₈₀₂/R₅₆₂-1)/( $\sqrt[]{R_{802} / R_{562}}$ +1)	[19]
MTCI	MERIS terrestrial chlorophyll index	(R₇₅₄-R₇₁₀)/(R₇₁₀-R₆₈₂)	[20]
GRVI	green ratio vegetation index	R₈₀₂/R₅₆₂	[21]
RVI	ratio vegetation index	R₈₀₂/R₆₈₂	[22]
VARI	visible atmospherically resistant index	(R₅₆₂-R₆₈₂)/(R₅₆₂+R₆₈₂-R₄₉₀)	[22]
TCARI	transformed chlorophyll absorption reflectance index	3[(R₇₀₂-R₆₇₀)-0.2(R₇₀₂-R₅₅₀)(R₇₀₂/R₆₇₀)]	[23]
SR	simple ratio	R₇₅₀/R₅₅₀	[24]
TVI	triangular vegetation index	0.5[120(R₇₅₂-R₅₅₀)-200(R₆₇₀-R₅₅₀)]	[25]
RDVI	renormalized difference vegetation index	(R₈₀₂-R₆₈₂)/ $\sqrt[]{R_{802} + R_{682}}$	[26]
PSRI	plant senescence reflectance index	(R₆₈₂-R₅₀₂)/R₇₅₀	[27]
ARVI	atmospherically resistant vegetation index	$\frac{R_{802} - [R_{682} - (R_{490} - R_{682})]}{R_{802} + [R_{682} - (R_{490} - R_{682})]}$	[28]
CRI	carotenoid reflectance index	1/R₅₁₀-1/R₅₅₀	[29]
MSAVI	modified soil adjusted vegetation index	0.5[2(R₈₀₂+1)- $\sqrt[]{(2 R_{802} {+ 1)}^{2} - 8 (R_{802} - R_{682})}$ ]	[30]

表1 本研究中的植被指数 Table 1 Vegetation indices

1.4.2 小波分析与特征提取

采用小波分析对数据进行去噪和分解^[31]。小波分析有两种形式: 连续小波变换(CWT)和离散小波变换(DWT)。 CWT比DWT更容易提取光谱特征和有用信息^[32], 因此采用CWT。 CWT是线性变换方法, 它利用丰富的母小波函数将高光谱反射率数据分解成不同频率的小波系数。母小波函数由式(2)定义^[33]

$Ψ_{a, b} (λ) = \frac{1}{\sqrt[]{a}} Ψ (\frac{λ - b}{a})$ (2)

式(2)中, Ψ _a_,_b(λ )是母小波函数, λ 表示频带数(λ =501), a为定义小波尺度的膨胀因子(a> 0), b表示确定小波位置的位移因子。 CWT的输出计算如式(3)

$W_{f} (a, b) = < f; Ψ_{a, b} > = \int_{-}^{\infty} f (λ) Ψ_{a, b} (λ) d λ$ (3)

式(3)中, f(λ )为450~950 nm范围内的原始光谱, W_f(a, b)为小波系数, 即由一维尺度(i=1, 2, 3, …, m, m=256)和波段(j=1, 2, 3, …, n, n=501)组成的二维小波系数尺度图(即m× n矩阵)。

CWT具有不同的小波母函数, 在实际应用中需要选择不同的小波函数进行不同的谱处理。其中Gaussian小波与其他小波函数相比, 不会出现明显的振荡或突变, 增加了信号处理和分析的稳定性。它可以更好地保留信号的局部特征, 更好地分析短期和局部特征。本研究采用CWT中的gaus2对光谱进行分解。

基于CWT提取了三种类型的小波特征: 通过Boruta对小波能量系数进行特征筛(Boruta-WFs); 采用小波能量系数与产量之间前1%的决定系数提取小波特征(1%R²-WFs); 单个分解尺度上的所有小波特征(SS-WFs)。本研究所有CWT相关分析均使用MATLAB 2021a进行, 工作流程如图2所示。

	Figure Option View Download New Window
	图2 小波特征提取流程Fig.2 Flowchart of wavelet geature extraction

(1)Boruta-WFs

Boruta是一种全相关特征选择方法, 通过计算每个输入预测器相对于阴影属性的Z-score^[34], 预测因子的重要因子由Z-score在指标中的分布决定^[35]。基于Boruta确定的重要因素, 采用最小最优特征选择策略, 进行排序和残差处理, 然后逐步建模。 Boruta算法的过程如下:

① 对特征矩阵X的每个特征值打乱, 将阴影特征与真实特征结合, 生成新的特征矩阵;

② 使用新的特征矩阵作为输入, 训练可以输出重要特征的模型;

③ 计算真实特征和阴影特征的Z值;

④ 找出阴影特征的最大Z-score, 标记为MZSA。

⑤ 将Z-score大于MZSA的真实特征标记为“ 重要” , 将Z-score明显小于MZSA的真实特征标记为“ 不重要” , 并将其从特征集中永久删除。

⑥ 删除所有阴影特征;

⑦ 重复①— ⑥, 直到所有特征都被标记为“ 重要” 或“ 不重要” 。

首先通过连续小波变换在不同的波段和尺度上得到多个结果。然后采用Boruta特征选择算法对多尺度的结果进行筛选, 该过程获得的特征被称为Boruta-WFs。本研究使用python包BorutaPy构建Boruta特征选择算法^[36]。

(2)1%R²-WFs

将计算得到的小波系数与成熟期收获的产量进行相关分析, 得到决定系数R²。不同尺度和不同波段小波系数的R²值形成相关尺度图, 表示各小波系数对产量的敏感性。通过对所有尺度上的R²值按降序排序, 保留R²值的前1%作为小波特征提取的1%R²-WFs。

(3)SS-WFs

CWT对不同位置和多尺度的光谱信息进行分解, 为了有效捕捉产量引起的光谱变化, 本研究选择了单一分解尺度下的小波系数作为小波特征: SS-WFs。

1.5 建模方法

为评估方法的有效性, 探究冠层高光谱反射率与小麦产量之间的关系, 本研究选择随机森林(random forests, RF)、 K最邻近(K-nearest neighbors, KNN)和极度梯度提升树(eXtreme gradient boosting, XGBoost)三种模型方法。机器学习模型使用Python 3.11实现, 通过随机搜索和内部5次交叉验证方法对模型的超参数进行了调整。

(1) 随机森林模型是一种以决策树为基础, 运用集成学习(ensemble learning)策略的预测模型。其中每棵树在其决策树中的每次拆分时使用预测变量的随机子集, 结合多个决策树的预测结果, 以提高整体模型的预测准确性和稳健性。其特性使其在解决多种预测问题, 包括分类和回归问题等方面具有优异的性能。其优势在于回归过程可以通过无偏估计评估每个特征的重要性, 在处理复杂的非线性关系时, 比传统的线性模型具有更高的效率^[37]。

(2) K最邻近是最典型的机器学习算法之一, 是一种非参数和惰性机器学习算法, 可用于解决分类和回归问题^[38]。其依赖于一个基于实例的学习概念, 假设一个新的预测变量和一个训练组之间的相似性, 然后将新的预测器分类到最相似的类别中^[39]。 KNN的优点在于其简单性, 有效性和处理复杂非线性关系的能力。

(3) 极度梯度提升树是一种基于梯度提升(gradient boosting)决策树用于解决分类或回归问题的增强集成算法, 在很多机器学习任务中展现出了卓越的性能。其核心思想是采用前一个弱分类器训练得到的残差作为参考, 优化下一个新的弱分类器。这种残差拟合方式可以有效减少训练样本的损失, 优化模型的复杂度, 从本质上提高模型的准确性和鲁棒性。传统的GBDT在优化中只使用一阶导数信息(负梯度), 而XGBoost使用一阶和二阶导数对成本函数进行二阶泰勒展开。

1.6 模型验证和评估

使用五折交叉验证法作为数据集划分方法, 五折交叉验证(5-fold cross-validation)是一种常用的模型验证方法, 旨在评估模型的泛化性能。五折交叉验证主要应用于小样本数据集, 最终选取平均值作为模型的最终性能。并使用选择决定系数(coefficient of determination, R²)和均方根误差(root mean squared error, RMSE)作为模型精度评价指标。上述计算方法分别见式(3)和式(4)。

$R^{2} = \frac{{(\overset{n}{\sum_{i = 1}} y_{i} - \overset{̅}{y})}^{2}}{{(\overset{n}{\sum_{i = 1}} x_{i} - \overset{̅}{y})}^{2}}$ (3)

$RMSE = \sqrt[]{\frac{\overset{n}{\sum_{i = 1, j = 1}} (x_{i} - y_{i})^{2}}{n}}$ (4)

式(3)和式(4)中: x_i为小麦产量实测值; y_i为小麦产量预测值; $\overset{̅}{y}$ 为小麦产量均值; n为样本个数。

2 结果与讨论

2.1 最优特征提取结果

2.1.1 光谱特征

对2020年— 2021年两年试验的不同生育期植被指数与小麦产量进行相关性分析, 冬小麦开花期和灌浆期构建的植被指数与产量的相关性分析结果如图3所示。除植被指数TCARI外, 所有植被指数均与产量的相关性绝对值超过0.5。大多植被指数与产量呈现较高的相关性。基于相关性结果, 选取每个时期相关性绝对值大于0.7来构建小麦产量估算模型。

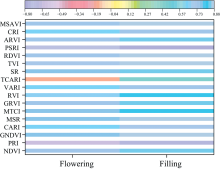	Figure Option View Download New Window
	图3 不同生育期植被指数与产量的相关系数 2.1.2 小波特征Fig.3 Correlation coefficient between vegetation indices and yield at different growth stages

(1) Boruta-WFs

首先经过连续小波变换得到不同尺度的小波系数, 通过Boruta算法对开花期和灌浆期两个生长阶段中影响产量的小波特征进行过滤, 划分为重要或不重要的特征。采用Boruta算法实施了100次迭代学习过程, 超过90%的特征被归类为不重要, 开花期选出37个重要特征, 灌浆期选出43个重要特征。采用Boruta算法的特征选择如图4(a, b)所示, 图中红点表示已选择的特征。表明随着分解尺度的增加, 小波分解所得的光谱细节逐渐变得模糊, 在第10尺度的小波系数已经出现重复性的锯齿状变化, 因此本研究只开展前10分解尺度的分析。前4个尺度的光谱变化都比较精细, 选择的特征大部分位于前4分解尺度。

	Figure Option View Download New Window
	图4 基于Boruta算法的特征选择 (a): 开花期; (b): 灌浆期Fig.4 Feature selection based on Boruta algorithm (a): Flowering; (b): Filling

(2) 1%R²-WFs

采用CWT生成的开花期和灌浆期的小波特征与产量相关的确定系数尺度如图5(a, b)所示, 其中提取的小波特征区域在图中用红色突出显示。结果表明, 开花期的R²取值范围为0~0.685, 前1%的R²值由高到低的阈值为0.582, 提取的WFs主要分布在较低的尺度, 2尺度的WFs最多, 4尺度中最少。这些特征集中在650~750 nm的红波段区域, 对映于原始光谱的敏感区域。灌浆期的R²值取值范围为0~0.794, 前1%的R²值由高到低的阈值为0.782, 提取的WFs主要分布在7尺度上的可见光区域和4尺度的近红外区域。两个生育期各选取了50个特征。所有生育期选择的50个特征均与产量呈高度显著相关(p值< 0.001)。

	Figure Option View Download New Window
	图5 开花期和灌浆期确定系数尺度图 (a): 开花期; (b): 灌浆期Fig.5 Scale diagram of determining coefficient at flowering and grouting stages (a): Flowering; (b): Filling

(3) SS-WFs

对原始反射率进行CWT, 生成10个尺度的WFs, 通过不同机器学习方法, 得到所有分解尺度下最优的单尺度模型。采用RF、 KNN和XGBoost算法, 在10个不同的分解尺度下独立构建小麦产量的预测模型, 每个模型都基于单个分解尺度下的所有小波特征。开花期和灌浆期的结果如图6(a, b)所示, 图6中展示了各生育期中不同算法的单尺度小波特征的R²和RMSE。在开花期中, RF、 KNN和XGBoost三种算法构建的模型均在第4分解尺度精度最高, R²分别为0.71、 0.49和0.72, RMSE分别为1.02、 1.36和1.00 t· ha^-1。在灌浆期中, 基于RF模型在第4尺度精度最高, R²和RMSE分别为0.75和0.95 t· ha^-1, 基于KNN和XGBoost模型均在第2尺度精度最高, R²分别为0.74和0.77, RMSE分别为0.96和0.13 t· ha^-1。

	Figure Option View Download New Window
	图6 单尺度分解所有小波特征的预测模型的精度 (a): 开花期; (b): 灌浆期Fig.6 Accuracy of the prediction model with single-scale decomposition of all wavelet features (a): Flowering; (b): Filling

2.2 小麦产量预测模型的评估

2.2.1 基于不同小波特征的模型比较

基于2020年与2021年数据, 以不同类型的小波特征作为输入参数, 分别采用RF、 KNN和XGBoost三种不同算法构建开花期和灌浆期小麦产量预测模型, 并评估和对比模型精度。针对各生育期的三种小波特征, 结合三种机器学习方法构建的小麦产量预测模型的精度如表2和表3所示。在开花期, 基于Boruta-WFs作为模型参数的输入时, 各个算法的R²分别为0.74、 0.53和0.73, RMSE分别为0.96、 1.30和0.99 t· ha^-1。在灌浆期, 基于Boruta-WFs作为模型参数的输入时, 各个算法的R²分别为0.79、 0.75和0.83, RMSE分别为0.87、 0.95和0.78 t· ha^-1。结果表明, 在相同的小波特征作为输入参数时, 两时期的Boruta-WFs结合三种机器学习方法构建的模型精度均优于1%R²-WFs和SS-WFs。由于1%R²-WFs忽略特征间非线性关系和容易受到数据中随机相关性的影响, SS-WFs对单尺度WFs中不相关特征的过滤不足, 导致模型的效率低。值得注意的是, Boruta算法通过创建阴影特征来模拟随机波动。一些看似有用但实际上不相关的随机扰动被消除, 而真正相关的特征被保留。这一特性让Boruta在特征选择中占据优势, 生成的模型可以只包含相关特征, 有助于更好地理解变量之间的复杂关系, 推动Boruta与机器学习的结合。因此选择合适的方法对小麦产量预测模型的准确性有重要影响。相比之下, Boruta-WFs在三种机器学习模型和不同生育期中始终表现出相对较高的准确性和出色的稳定性。本研究认为Boruta-WFs更适合作为小麦产量预测模型的代表性小波特征。

表2 基于开花期不同类型小波特征的小麦产量预测模型精度 Table 2 Accuracy of wheat yield prediction model based on different types of Wavelet Features at flowering stage

表3 基于灌浆期不同类型小波特征的小麦产量预测模型精度 Table 3 Accuracy of wheat yield prediction model based on different types of Wavelet Features at filling stage

2.2.2 基于最优小波特征与光谱特征模型比较

基于光谱特征中选择相关性绝对值大于0.7的植被指数, 开花期选出11个VIs(NDVI、 GNDVI、 MSR、 MTCI、 GRVI、 SR、 TVI、 RDVI、 PSRI、 ARVI和MSAVI); 灌浆期除TCARI外, 其余VIs相关性绝对值都大于0.7, 选出16个。确定Boruta-WFs作为最佳小波特征, 采用RF、 KNN和XGBoost三种不同算法, 分别以小麦不同生育期筛选后的光谱特征为输入参数, 比较最优小波特征Boruta-WFs和光谱特征小麦产量预测模型的性能。图7和图8给出了基于不同机器学习算法以各生育期的Boruta-WFs和光谱特征作为输入参数构建小麦产量模型预测值与实测值的散点图。由图7和图8可知, 以光谱特征作为输入的模型, 开花期中R²分别0.63、 0.51和0.52, RMSE分别为1.14、 1.32和1.31 t· ha^-1; 灌浆期R²分别0.71、 0.71和0.71, RMSE分别为1.01、 1.02和1.01 t· ha^-1。相比之下, 光谱特征对小麦产量的预测效果不佳, 两个不同生育期中基于Boruta-WFs的产量预测模型的精度高于光谱特征, 开花期R²分别提高了17.5%、 4%和39.6%, 灌浆期的精度分别提高了8.4%、5.6%和16.9%。因此, 灌浆期采用Boruta-WFs能够提取光谱与小麦产量之间更有效的信息, 结合XGBoost模型可实现对小麦产量的精准估测。

	Figure Option View Download New Window
	图7 开花期以Boruta-WFs(a)和VIs(b)为输入的实测产量与预测产量的散点图Fig.7 Scatterplot of measured and predicted yield with Boruta-WFs (a) and VIs (b) as inputs at flowering stage

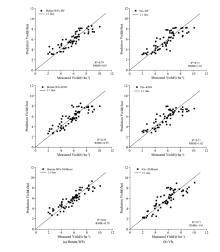	Figure Option View Download New Window
	图8 灌浆期以Boruta-WFs(a)和VIs(b)为输入的实测产量与预测产量的散点图Fig.8 Scatterplot of measured and predicted yield with Boruta-WFs (a) and VIs (b) as inputs at filling stage

由表2和表3可知, 小波特征在小麦产量预测方面表现良好, 证明了CWT与机器学习结合用于产量预测的可行性。分析基于最优小波特征和光谱特征作为预测因子模型的性能。两个生育期中, 基于Boruta-WFs的结合3种机器学习方法的精度均比光谱特征的高, 这可能是由于CWT在不同位置对光谱信息进行了多尺度分解引起的水分、形态和结构的光谱变化和Boruta算法在对位置和尺度进行了优化特征筛选。通过Boruta算法对影响产量的重要波段进行过滤, 避免特征间的共线性, 对于大多数机器学习算法, 重要波段有助于提高预测精度, 表明使用Boruta算法进行特征选择有效。

作物的生理特性随作物生长阶段的不同而变化, 灌浆期是光合作用产生的淀粉、蛋白质等有机物质从营养器官向籽粒转移的时期。灌浆期的小波特征和VIs直接反映了冬小麦的最终生长状态, 因此灌浆期的产量预测精度最高。本研究灌浆期结合Boruta-WFs和XGBoost的模型在所有生育期和模型中表现最好, R²为0.83, RMSE为0.78 t· ha^-1。

3 结论

采用小麦冠层高光谱数据, 通过CWT分别提取Boruta-WFs、 1%R²-WFs和SS-WFs三种不同类型的小波特征, 结合RF、 KNN和XGBoost三种机器学习方法构建小麦2个生育期的产量预测模型。结果表明: (1)开花期和灌浆期, 基于不同类型的小波特征, 以Boruta-WFs作为模型变量构建的小麦产量预测模型精度高于1%R²-WFs和SS-WFs。 (2)结合Boruta-WFs和XGBoost构建的模型精度比光谱特征更高, 灌浆期的R²为0.83, RMSE为0.78 t· ha^-1。 (3)基于小波特征和光谱特征构建的小麦产量估算模型均表现为灌浆期效果较好。

本研究提出了一种结合Boruta-WFs和机器学习方法的小麦产量预测模型, 结果证明模型精度优于其他WFs和光谱特征, 为小麦产量的预测提供了一种新的预测方法。值得注意的是, 未来的研究还需要获得不同地区样本作为独立的数据集进行验证, 以得到普适的小麦估产模型。

参考文献

文献列表

[1]	Xue H, Xu X, Zhu Q, et al. Computers and Electronics in Agriculture, 2024, 218: 108731. [本文引用:1]
[2]	Chaofa B, Hongtao S, Suqin W, et al. Remote Sensing, 2022, 14(6): 1474. [本文引用:1]
[3]	Wei Y, Tyler N, Ziyuan H, et al. Computers and Electronics in Agriculture, 2021, 184: 106092. [本文引用:1]
[4]	Fu Y, Yang G, Wang J, et al. Computers and Electronics in Agriculture, 2014, 100: 51. [本文引用:1]
[5]	Messina G, Modica G. Remote Sensing, 2020, 12(9): 1491. [本文引用:1]
[6]	XIAO Lu-jie, YANG Wu-de, FENG Mei-chen, et al(肖璐洁, 杨武德, 冯美臣, 等). Chinese Journal of Ecology(生态学杂志), 2022, 41(7): 1433. [本文引用:1]
[7]	CUI Huai-yang, XU Hui, ZHANG Wei, et al(崔怀洋, 徐晖, 张伟, 等). Journal of Triticeae Crops(麦类作物学报), 2015, 35(8): 1155. [本文引用:1]
[8]	Liu Y, Sun L, Liu B, et al. Remote Sensing, 2023, 15(19): 4800. [本文引用:1]
[9]	Yang L, Haikuan F, Jibo Y, et al. Remote Sensing, 2022, 14(21): 5449. [本文引用:1]
[10]	Liu Y, Sun L, Liu B, et al. Remote Sensing, 2023, 15(19): 4158. [本文引用:1]
[11]	Li Y, Zeng H, Zhang M, et al. International Journal of Applied Earth Observation and Geoinformation, 2023, 118: 103269. [本文引用:1]
[12]	Joshi A, Pradhan B, Chakraborty S, et al. Ecological Informatics, 2023, 77: 102194. [本文引用:1]
[13]	Xiaokai C, Fenling L, Qingrui C. Remote Sensing, 2023, 15(4): 997. [本文引用:1]
[14]	Haojie L, Minzan L, Junyi Z, et al. International Journal of Agricultural and Biological Engineering, 2018, 11(6): 132. [本文引用:1]
[15]	Cheng T, Riaño D, Ustin S L. Remote Sensing of Environment, 2014, 143: 39. [本文引用:1]
[16]	Fitzgerald M A, Mccouch S R, Hall R D. Trends in Plant Science, 2008, 14(3): 133. [本文引用:1]
[17]	Gitelson A A, Kaufman Y J, Merzlyak M N. Remote Sensing of Environment, 1996, 58(3): 289. [本文引用:1]
[18]	Gamon J A, PeñUelas J, Field C B. Remote Sensing of Environment, 1992, 41(1): 35. [本文引用:1]
[19]	Li Z, Li Z, Fairbairn D, et al. Computers and Electronics in Agriculture, 2019, 162: 174. [本文引用:1]
[20]	Dash J, Curran P J. IEEE International Geoscience & Remote Sensing Symposium, 2004, 25(549): 151. [本文引用:1]
[21]	Houborg R, Mccabe M F. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 135: 173. [本文引用:1]
[22]	Han L, Yang G, Dai H, et al. Plant Methods, 2019, 15(1): 1. [本文引用:1]
[23]	Hernand ez-Clemente R, Navarro-Cerrillo R M, Zarco-Tejada P J. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 5206. [本文引用:1]
[24]	Yiguang F, Haikuan F, Jibo Y, et al. Remote Sensing, 2023, 15(3): 602. [本文引用:1]
[25]	Liu Y, Liu S, Li J, et al. Computers and Electronics in Agriculture, 2019, 166: 105026. [本文引用:1]
[26]	Yue J, Yang G, Tian Q, et al. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 150: 226. [本文引用:1]
[27]	Zhang X, Zhao J, Yang G, et al. Remote Sensing, 2019, 11(23): 2752. [本文引用:1]
[28]	Kaufman Y J, Tanre D. IEEE Trans. Geosci. Remote Sens. , 1992, 30(2): 261. [本文引用:1]
[29]	Penuelas J, Baret F, Filella I. Photosynthetica, 1995, 31(2): 221. [本文引用:1]
[30]	Qi J, Chehbouni A, Huete A R, et al. Remote Sensing of Environment, 1994, 48(2): 119. [本文引用:1]
[31]	Ebrahimi H, Rajaee T. Global and Planetary Change, 2017, 148: 181. [本文引用:1]
[32]	Hongfei Y, Yurong Q, Feng Y, et al. Soil Science, 2012, 177(11): 674. [本文引用:1]
[33]	Bruce L M, Morgan C, Larsen S. IEEE Trans. Geoscience and Remote Sensing, 2001, 39(10): 2217. [本文引用:1]
[34]	Zhang N, Chen M, Yang F, et al. Remote Sensing, 2022, 14(18): 4434. [本文引用:1]
[35]	Kursa M B, Jankowski A, Rudnicki W R. Fundamenta Informaticae, 2010, 101(4): 271. [本文引用:1]
[36]	Degenhardt Frauke, Seifert Stephan, Szymczak Silke. Briefings in Bioinformatics, 2019, 20(2): 492. [本文引用:1]
[37]	Hong Y, Chen S, Chen Y, et al. Soil & Tillage Research, 2020, 199: 104589. [本文引用:1]
[38]	Tianao W, Wei Z, Xiyun J, et al. Computers and Electronics in Agriculture, 2021, 184: 106039. [本文引用:1]
[39]	Maria B, Chris C, Aris K. Remote Sensing, 2022, 14(16): 3880. [本文引用:1]