引用本文
陈恒杰, 方旺, 张家伟, 陈双扣. 2,5-二氯嘧啶振动光谱的实验和理论研究[J]. 光谱学与光谱分析, 2024,44(10): 2795-2804.
CHEN Heng-jie, FANG Wang, ZHANG Jia-wei, CHEN Shuang-kou. The Experimental and Theoretical Study of Vibrational Spectroscopy for 2,5-Dichloropyrimidine[J]. Spectroscopy and Spectral Analysis, 2024,44(10): 2795-2804.
Doi:10.3964/j.issn.1000-0593(2024)10-2795-10  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
2,5-二氯嘧啶振动光谱的实验和理论研究
陈恒杰1, 方旺1, 张家伟1,*, 陈双扣2
1. 重庆科技大学数理与大数据学院物理系, 重庆 401331
2. 重庆科技大学化学化工学院应用化学系, 重庆 401331
*通讯作者 e-mail: physics_zjw@126.com

作者简介: 陈恒杰, 1980年生,重庆科技大学数理与大数据学院物理系副教授 e-mail: nwwolfchj@gmail.com

收稿日期: 2023-05-08 修回日期: 2024-01-08
基金: 国家自然科学基金项目(12275036),重庆市科学技术局(cstc2019jcyj-msxmX0147, cstc2021jcyj-msxmX0681)和重庆市教委(KJQN202001541)资助
摘要

采用KBr压片(KBr)、 石蜡油(Nujol)、 衰减全反射(ATR)和熔融(Liquid)四种样品制备方法, 收集了2,5-二氯嘧啶(2,5-DCP)固相及液相、 400~4 000 cm-1范围内的傅里叶变换红外光谱(FTIR), 记录了80~3 200 cm-1区间内的傅里叶变换拉曼光谱(FT-Raman)和激光拉曼光谱(Laser-Raman)被记录。 为正确解释实验获得的振动光谱, 首先采用14种密度泛函理论方法(DFT)及二阶微扰理论(MP2)对2,5-DCP的结构进行优化, 获得谐性近似下的振动频率、 红外强度和拉曼活性, 并将拉曼活性转换到拉曼强度。 进一步考虑非谐效应, 在平衡结构附近展开微扰计算, 得到简振坐标下的三阶、 四阶力场, 以振动二阶微扰(VMP2)理论得到2,5-DCP的非谐振动频率和非谐振动强度, 发现B3LYP计算的非谐振动频率与实验值差异最小。 基于优选的B3LYP方法, 继续考察基组对振动频率的影响, 通过9种基组计算结果发现6-311++G(2pd, 2df)获得的非谐振动频率最佳, 其与实验值的均方根误差(RMSE)为6.75 cm-1(22个振动模下为4.63 cm-1), 6-311++G(d, p)在大大减少计算时间的同时, 精度未有多大损失(6.79 cm-1)。 综上所述, 基于B3LYP方法结合6-311++G(2df, 2pd)基组得到的非谐振动光谱是归属2,5-DCP实验光谱的最佳选择。 基于最优计算结果、 标度因子方法获得的振动基频, 结合非谐红外振动强度、 谐性近似下的拉曼强度、 简振坐标示意图以及振动势能分布(PED), 对比到实验采集的红外和拉曼光谱, 对2,5-DCP的所有基频和部分泛频进行了指认, 发现两个振动耦合, 一为3 054 cm-1与1 554以及1 540 cm-1的和频耦合导致; 二为1 132 cm-1与793+351 cm-1和频及1 370~230 cm-1差频耦合引起。 最后预期了多个同位素取代下的2,5-DCP振动谱, 同时检验了上述归属的正确性。

关键词: 2; 5-二氯嘧啶; 红外光谱; 拉曼光谱; 非谐效应; 势能分布; 同位素效应
中图分类号:O657.3 文献标志码:A
The Experimental and Theoretical Study of Vibrational Spectroscopy for 2,5-Dichloropyrimidine
CHEN Heng-jie1, FANG Wang1, ZHANG Jia-wei1,*, CHEN Shuang-kou2
1. Department of Physics, School of Mathematics, Physics and Data Science, Chongqing University of Science and Technology, Chongqing 401331, China
2. Department of Applied Chemistry, School of Chemistry and Chemical Engineering, Chongqing University of Science and Technology, Chongqing 401331, China
*Corresponding author
Abstract

Fourier transforms infrared (FT-IR) spectra in the range of 400~4 000 cm-1 was ollected for 2,5-dichloropyrimidine (2,5-DCP) in solid phase as well as in liquid phase using four sample preparation methods: KBr pressed (KBr), mineral oil (Nujol), attenuated total reflection (ATR) and melting (Liquid), while Fourier transforms Raman (FT-Raman) and laser Raman (Laser-Raman) spectra in the range of 80~3 200 cm-1 was also recorded. To correctly interpret the experimentally obtained vibrational spectra, the geometry of 2,5-DCP was first optimized by applying 14 methods from density function theory (DFT) as well as second-order perturbation method (MP2), based on which its harmonic frequency, infrared intensity and Raman activity were obtained, followed by the conversion of Raman activity to Raman intensity. To consider the anharmonic effect, the perturbation calculation is performed near the equilibrium geometry to obtain the third and fourth-order force fields in normal coordinates, and the anharmonic vibration frequency and intensity of 2,5-DCP are obtained based on the vibration second-order perturbation (VMP2) theory. It is found that the anharmonic vibration frequencies calculated by B3LYP and B3PW91 have the smallest difference from the experimental values. Based on the preferred B3LYP method, the effect of the basis sets on the vibration frequency continued to be investigated, eight basis sets were adopted, and it was found that the difference between the 6-311++G(2pd, 2df) level and the experimental values was the smallest, with a root-mean-square error(RMSE) of 6.75 cm-1 (4.63 cm-1 under 22 vibration modes), the 6-311++G(d, p) greatly reduced the calculation time, while the accuracy of 6-311++G(d, p) is not much lost (6.79 cm-1). In summary, the anharmonic vibrational spectra calculated based on the B3LYP method combined with the 6-311++G(2df, 2pd) basis set are the best choice for assigning the experimental vibrational spectra of the 2,5-DCP. Then, according to the optimal calculation results and the vibrational fundamental frequencies obtained by the scaling factor method, combined with the anharmonic vibrational intensity, the schematic diagram of the normal coordinates analysis, the potential energy distribution (PED) of the vibrations, and compared to the experimentally acquired infrared and Raman spectra, all fundamental frequencies and some overtones of the 2,5-DCP were assigned, and two vibrational couplings were found, One is caused between 3 054 cm-1 and the combination tones of 1 554 and 1 540 cm-1; the other is from the coupling between 1 132 cm-1 and the sum frequency 793+351 cm-1 and the difference frequency 1 370~230 cm-1. Finally, the anharmonic vibrational spectra of 2,5-DCP under multiple isotopic substitutions were expected and the correctness of the attribution was checked again.

Keyword: 2; 5-Dicholoropyrimidine; Infrared spectra; Raman spectra; Anharmonic effect; Potential energy distribution(PED); Isotope effect
引言

作为一类重要的杂环化合物, 嘧啶及其衍生物具有优异的物理和化学性能, 2, 5-二氯嘧啶(2, 5-DCP)常用于原材料或中间体[1], 在生物、 化工和制药等有广泛的应用, 对其结构和光谱的研究具有重要意义。 1996年, Alexander等通过电子衍射法首次测定了2, 5-二氯嘧啶的分子结构[2]; 2011年, Tran等提出了一种新颖的五步合成方法[3], 后被一种更有效的两步合成技术取代[4], 针对2, 5-二氯嘧啶振动光谱的文献研究依然空白。 众所周知, 随分子尺度增大, 振动光谱归属变得越发困难, 尽管基于谐性力场的计算可提供粗略的理论指导, 但实验光谱与计算值间仍存在较大差异, 特别在高波数段, 重要原因是模型中未考虑非谐效应和分子间相互作用。 近年, Barone等对此进行了一系列工作, 振动自洽场(VSCF)、 振动二阶微扰理论(VMP2)和振动组态相互作用(VCI)等先后建立[5], 相关研究不断报道; Yu等用VSCF结合四阶力场(QFF)对分子的非谐性进行研究[6], Anna等用同样的方法对气态甲酸的顺式和反式结构进行了报道[7], Kale等在耦合团簇理论(CC)下结合VPT2以及四阶力场对丁自由基的多种异构体进行了非谐计算, 并据此解释和归属了实验光谱[8]。 鉴于资源和效率考虑, 即使对中等尺度分子, 耦合簇理论的非谐计算亦是一项艰巨任务, 因此基于密度泛函(DFT)的非谐效应研究依然占据主流。

本工作记录了多种样品制备模式下2, 5-DCP分子的傅里叶变换红外光谱(FTIR), 收集了其傅里叶拉曼(FT-Raman)和激光拉曼 (Laser-Raman)光谱; 采用14种DFT方法和9个基组开展非谐计算, 优选出结果对解释和归属实验光谱最佳的组合; 在此基础上, 基于非谐计算、 振动势能分布(PED)、 标度因子和简振示意图等方法获得的结果对2, 5-DCP分子的振动光谱进行全面归属; 最后预测了多个同位素取代(D, 13C, 14C, 15N, 37Cl)下2, 5-DCP的振动光谱。

1 实验部分

实验用2, 5-二氯嘧啶样品纯度98%。 傅里叶变换红外光谱(FTIR)待测样品通过四种方法准备, 分别为熔融法(Liquid)、 KBr压片法(KBr)、 石蜡油法(Nujol)和衰减全反射(ATR)法, 熔融法制样时, 先将样品加热至液体状态, 快速置于两盐片间形成液膜并马上测量, 其余样品均为固体状态。 通过配备了KBr分束器和DTGS探测器的Bruker VERTEX70光谱仪, 在分辨率为2 cm-1时记录了目标分子在400~4 000 cm-1(ATR为650~4 000 cm-1)范围内的红外光谱。 波长在80~3 200 cm-1的傅里叶变换拉曼光谱(FT-Raman)通过配备了Bruker FRA 106/S组件, 工作在Ge探测器和液氮温度下的VERTEX70光谱仪记录, 激光束采用钇铝石榴石(Nd∶ YAG), 波长为1 064 nm。 激光拉曼光谱(Laser-Raman)测量时, 先将样品置于石英比色皿中, 采用波长为633 nm 的LabRAM HR激光拉曼光谱仪连续采集。

2 理论

如图1所示, 2, 5-二氯嘧啶具有C2v对称性。 计算使用电子结构程序包Gaussian 09[9], 收敛标准设置为Verytight, 积分格点采用Ultrafine。 首先, 优化获得基态下2, 5-DCP的平衡几何结构, 基于该结构计算谐性近似下的振动频率、 红外强度和拉曼活性, 并将拉曼活性转换为拉曼强度。 进一步对上述解析方法得到的谐性力场进行数值微分, 抽取关于简振坐标的三阶和四阶导数, 构建相应的非谐势能面, 在此基础上基于振动二阶微扰理论(VPT2)获得非谐振动频率及红外强度。 最后借助于势能分布(PED)等对振动光谱进行归属, PED部分由VEDA4程序完成[10]。

图1 2, 5-二氯嘧啶分子结构Fig.1 Molecular geometry of 2, 5-Dichloropyrimidine

3 结果与讨论
3.1 DFT方法、 基组优选

理论上准确的振动光谱依赖于良好的平衡几何结构, 本工作先采用14种DFT以及二阶微扰理论(MP2)方法对2, 5-DCP的结构进行优化, 结果与实验值一起列于表1。 所有DFT方法得到的键长、 键角与气相及晶体实验结果接近, LC-BLYP获得的键长总体偏小, BHandHLYP在C2-N3, N3-C4, C4-C5和C4-H8处计算的键长偏短, 但在C2-Cl7和C5-Cl9处与实验相近; 理论上, MP2具有较高的精度, 而其与实验值偏差反而最大, 主要原因是所采用的基组aug-cc-pVDZ较小; 无论键长还是键角, 来自TPSSh的计算值与气相实验结果非常吻合, B3LYP、 TPSSh间差异非常小, 例如, B3LYP计算的键长C2-N3, N3-C4分别为1.323、 1.330 Å , 对应的TPSSh值为1.326、 1.333 Å ; 包含色散项的B3LYP-D在几何结构上并没有比B3LYP有显著改善, 与2, 5-DCP色散作用不强有关; 一些其他DFT方法, 如: CAM-BLYP, M062X, WB97XD, tHCTH和M11也未得到更接近实验的几何结构, 说明对2, 5-DCP基态, B3LYP依然是行之有效的结构优化方法。

表1 不同理论方法下2, 5-二氯嘧啶分子的结构参数 Table 1 Geometrical parameters of 2, 5-Dichloropyrimidine at different methods

尽管上述结果显示B3LYP方法是基态平衡结构获取的不错选择, 而目前并没理由显示其得到的振动光谱对归属实验光谱同样最佳, 因此, 对2, 5-DCP的振动频率进行令人信服的理论计算至关重要。 表2为不同DFT水平下获得的非谐振动频率, 图2为各计算结果与实验值间的差异, B3LYP获得的非谐振动频率依然与实验符合最好, 除3 051和3 039 cm-1外的22个振动模与实验值的均方根误差(RMSE)为4.63 cm-1, 全部24个振动模的差异略有增大为6.75 cm-1, 分析认为高波段的非谐效应增加导致, 考虑了色散校正和长程校正的DFT并未改善振动频率值。 进一步采用优选的B3LYP在不同基组下考察, 结果见表3和图3, 可以看出6-311++G(2df, 2pd)基组得到的RMSE最小, 6-311++G(d, p)在大大减少计算时间的同时, 其精度仅有0.04 cm-1的损失, 是一种不错的选择, TZV的总体误差最大, 其余基组差异并不明显。 MP2与aug-cc-PVDZ组合大大增加了计算时间, 但RMSE依然巨大, 间接说明了密度泛函使用的合理和有效性。 综上所述, B3LYP方法结合6-311++G(2df, 2pd)基组为优选, 以下除特别申明, 计算值均来自于该组合结果。

表2 不同理论方法下的非谐振动频率 Table 2 Vibrational wavenumbers obtained from different methodsa

图2 不同理论方法下24个振动模的非谐振动频率与实验值偏差Fig.2 Deviation of anharmonic vibrational frequencies between different methods and experiments at 24 modes

表3 B3LYP下不同基组的非谐振动频率 Table 3 Vibrational wavenumbers obtained from different basis sets at B3LYP theoretical level

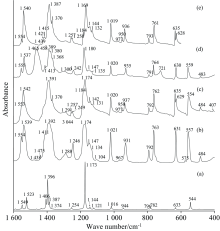
图3 不同基组下的非谐振动频率与实验值偏差Fig.3 Deviation of anharmonic vibrational frequencies between different basis sets and experiments

3.2 振动光谱及其归属

除SDBS光谱数据库中收录有一个低分辨透射谱外[11], 没有任何文献对2, 5-DCP的振动光谱进行过实验或理论报道。 图4(a— e)分别显示了该分子在2 600~3 200 cm-1范围内的红外光谱, 相应的拉曼光谱见图5(a, b, c), 400~1 600 cm-1的红外光谱、 80~1 600 cm-1的拉曼光谱分别收录于图6(a— e)和图7(a, b, c)。 计算值和多个实验结果见表4, 其中计算值包括谐性频率、 基于标度因子的校正频率(> 1 600 cm-1标度因子用0.973 73, 其余0.957 75)、 谐性近似下的红外强度和拉曼活性、 非谐振动频率、 基于非谐近似的红外强度及由谐性近似下的拉曼活性转换而来的拉曼强度。 基于简振坐标分析得到各振动模的势能分布(PED), 结合图8给出的简振示意图, 对各振动带进行全面归属。

图4 2, 5-二氯嘧啶在2 600~3 200 cm-1的红外光谱
(a): Anharmonic; (b): Liquid; (c): KBr; (d): Nujol; (e): ATRFig.4 FTIR spectra of 2, 5-Dichloropymidine at 2 600~3 200 cm-1
(a): Anharmonic; (b): Liquid; (c): KBr; (d): Nujol; (e): ATR

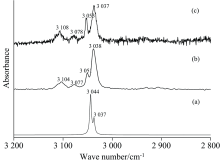图5 2, 5-二氯嘧啶在2 800~3 200 cm-1的拉曼光谱
(a): Anharmonic; (b): FT-Raman; (c): Laser-RamanFig.5 Raman spectra of 2, 5-Dichloropymidine at 2 800~3 200 cm-1
(a): Anharmonic; (b): FT-Raman; (c): Laser-Raman

图6 2, 5-二氯嘧啶在400~1 600 cm-1的红外光谱
(a): Anharmonic; (b): Liquid; (c): KBr; (d): Nujol; (e): ATRFig.6 FTIR spectra of 2, 5-Dichloropymidine at 400~1 600 cm-1
(a): Anharmonic; (b): Liquid; (c): KBr; (d): Nujol; (e): ATR

图7 2, 5-二氯嘧啶在80~1 600 cm-1的拉曼光谱Fig.7 Raman spectra of 2, 5-Dichloropymidine at 80~1600 cm-1
(a): Anharmonic; (b): FT-Raman; (c): Laser-Raman

表4 2, 5-二氯嘧啶的振动光谱归属 Table 4 Assignment of vibrational spectra for 2, 5-Dichloropymidine

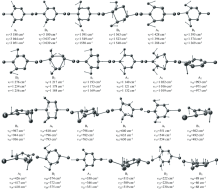图8 2, 5-二氯嘧啶简振示意图Fig.8 Vibrational schematic diagram of 2, 5-Dichloropymidine
(Symmetry, harmonic, anharmonic and experimental wavenumber)

2, 5-DCP由10个原子构成, 理论上有24个简正振动模式, 基态呈C2v对称性, 由群论知识可将其归属于9个A1、 5个B1、 8个B2和2个A2的不可约表示。 因有些带强度很小甚至禁阻, 实验中不易被观测到; 一些振动带十分接近, 重叠严重, 超出了仪器或检测水平下的分辨能力; 还有些远红外谱带不在中红外仪器检测范围; 还有部分泛频带和杂质吸收带的干扰; 欲对2, 5-DCP的振动光谱进行归属, 首先应在实验光谱中排除非目标分子的谱带。 因Nujol测量时混有石蜡油, 其主要成份为饱和长直链碳氢化合物, 图4(d)中两个强度极大的峰2 957和2 873 cm-1, 并未在其他红外和拉曼测量中出现, 分析其来自于石蜡油中甲基(CH3)的反对称和对称伸缩振动, 相应亚甲基(CH2)的反对称伸缩振动和对称伸缩振动位于2 927和2 857 cm-1; 图6(d)中的1 458 cm-1对应到CH3的不对称变角振动, 对称变角振动产生1 380 cm-1峰; CH2仅有一个变角振动, 位于1 465 cm-1, 1 300 cm-1处的弱吸收峰来自于CH2的扭曲振动, 721 cm-1处的中等吸收峰由CH2的面内摇摆引起[12], 由石蜡油中饱和烷烃引起的振动峰被全部识别, 剩余峰来自于2, 5-DCP的基频或泛频。

2, 5-DCP在2 600~3 200 cm-1的峰主要有3 039, 3 051, 3 079和3 100 cm-1。 Liquid下, 3 051和3 079 cm-1两峰因重叠被淹没, 归因于较高的液体浓度, 由比尔朗伯定律, 在其他三种方式下强度较弱的两峰2 716和2 690 cm-1改变十分明显, 同时提示为了研究某些低强度振动峰, 特别对强度普遍偏弱的泛频峰, 可通过增大样品浓度实现对应振动峰的记录, 非谐计算表明, 1 600~3 000 cm-1间并无2, 5-DCP的基频振动峰, 则其必然是该物质的泛频峰。 比较其他测量方式, Liquid下测得的3 040 cm-1峰有4 cm-1的红移, 可能由固液相分子间力的差异导致。 Nujol下, 来自石蜡油中的甲基和亚甲基具有很大的振动强度, 相比之下3 041和3 107 cm-1的强度相对较弱, 在图4(d)中并不明显, 事实上, 当局部放大该处谱图时, 依然十分清楚的显现出两峰。 谐性近似下, 该波段的两个峰均为3 180 cm-1, 不仅没能被区分, 对应的谐振频率也远离实验值, 间接说明高波段处非谐计算的必要性。 由表4非谐计算, 3 044 cm-1振动峰在2 600~3 200 cm-1波段具有最大的红外和拉曼强度, PED分析、 简振示意图均支持其来自于2, 5-DCP上CH的伸缩振动(A1, 99%), 具有B2对称性, 强度大约是CH反对称伸缩振动峰3 037 cm-1(100%)的三倍, 然而实验结果显示峰3 044 cm-1的强度远弱于峰3 037 cm-1, 在红外光谱上这种对比更加明显, 位于3 100 cm-1处的泛频峰强度却明显大于基频峰3 054 cm-1, 显然不合常理, 经分析3 079和3100 cm-1分别为1 540和1 553 cm-1的和频, 两峰对称性直积后均为A1对称性, 与波数差距不大且具有同样A1对称性的3 054 cm-1产生费米共振, 导致能量转移, 引起3 054 cm-1峰强减小, 3 100、 3 079 cm-1两峰强度增加。 截止目前, 本研究完成了2 600~3 200 cm-1内几个振动峰的归属。

计算显示, 无论红外还是拉曼光谱, 最强的几个峰出现在400~1 600 cm-1区间, 强红外峰主要有1 173和1 396 cm-1, 其次为1 523, 544和1 549 cm-1峰, 与图6实验结果一致, 对称性依次为A1, B2, B2, A1和A1; 拉曼强峰依次为346、 1 121、 796和1 549 cm-1, 图7实验中, 351与793 cm-1处计算的强度与计算结果完全吻合, 但计算对1 127和1 550 cm-1峰强有所高估。 同样由于浓度偏大, 图6(b)中的几个高强度峰(如: 1 392、 1 174 cm-1)达到饱和。 635/629 cm-1、 1 257/1 250 cm-1等峰在KBr和ATR测量中发生了分裂, 2, 5-DCP在80~1 600 cm-1间的振动光谱可归属为图6(a— e)。

3.2.1 C-H振动

图8清晰反映出非谐计算的1 396 cm-1峰由两个CH键在面内剪切振动形成(69%), 标度因子、 实验值均集中在1 390 cm-1附近。 反观谐性计算, 其结果为1 428 cm-1, 与实验值差异约40 cm-1, 由于该峰附近振动信息丰富, 极易导致归属错误, 进一步说明非谐计算的必要性。 1 388 cm-1在红外光谱中强度最大, 说明振动时偶极矩变化大, 在FT-Raman中虽然较弱, 但清晰可见, 表明该振动导致的极化率变化较小, 该峰在Laser-Raman中没有任何信号, 可能与采集时间偏少有关。 1 374和1 254 cm-1, 主要归属为两CH键的面内摇摆振动, 同时带动相连的两CN键振动引起, 但前者靠近氢键的两CN键振动相位相反, 后者一致, 即当两CN键随CH键振动时, 1 374 cm-1处的振动对应的C4N3与C6N1键长同增或同减; 相反, 1 254 cm-1 振动对应的C4N3与C6N1的键长变化互异, 两振动均属于B2对称。 计算表明, 1 254 cm-1的红外振动强度和拉曼活性都比较小, 对应的拉曼强度比1 388 cm-1更小, 实验结果支持当前计算, ATR和KBr测量, 该峰分裂成了1 249和1 257 cm-1。 经分析1 257为635 cm-1的倍频峰; CH键的面外变形形成两峰, 计算显示其位于971和944 cm-1, 对应的实验值为977和937 cm-1, 其中971 cm-1几乎为CH键的面外扭曲振动(97%), 红外强度和拉曼活性均很弱, 944 cm-1主要为CH键的面外摇摆振动(92%), 红外强度一般, 拉曼强度趋近于零, 当前计算与图6, 图7实验结果一致。

3.2.2 C-C、 C-N振动

由于C、 N同处嘧啶环上, 两者振动往往相耦合, 由嘧啶环上六个原子间相互做反对称伸缩引起的振动峰于1 184 cm-1, PED占97%, 具体振动形式见图8, 因受到附近强峰1 169 cm-1的影响, 在ATR和KBr测量中, 该振动以肩峰形式出现, Liquid测量中, 由于高浓度的影响, 1 184 cm1被淹没在1 169 cm-1中并最终融合成1 174 cm-1峰。 2, 5-DCP中, 最强的红外峰由远离氢原子侧的C2N1N3Cl7面内剪切振动引起(62%), 另外耦合了12%的CH面内剪切振动, 红外和拉曼实验均显示其位于~1 170 cm-1, FT-Raman光谱中清晰展现了1 184和1 170 cm-1峰, 非谐计算也表明最强的红外振动峰于1 173 cm-1, 其强度达278 km· mole-1, 附近1 178 cm-1处还存在一强度很弱的峰, 实验与计算完全吻合。 整个C、 N原子协同振动形成了嘧啶环的呼吸振动, 非谐计算显示其位于1 121 cm-1处, 具有最强的拉曼峰, 实验中离其最近的红外峰为1 132 cm-1, FT-Raman则移动到1 127 cm-1, 周边还有1 132和1 143 cm-1, 强度均为中等偏弱, 结合泛频理论和群论知识, 可得1 143为793和351 cm-1的和频, 1 134为1 370和230 cm-1的差频, 两者均具有A1对称性, 与1 132 cm-1处的呼吸振动产生耦合, 使得对称性相同的差频和合频振动峰强度增大, 基频振动峰1 132 cm-1强度减弱。 另外三种面内剪切振动形式分别对应到1 020、 792和633 cm-1, 前两者为A1, 633 cm-1属于B2对称性, 1 020 cm-1具有中等强度的红外峰, 对应拉曼强度非常小, 且周边无其他峰影响, 792 cm-1具有很强的拉曼强度, 结合非谐计算, 两者很容易被归属。 ATR和KBr下, 630 cm-1分裂为630和635 cm-1两个峰, 结合数值计算, 得到所有基频可能的倍频、 和频和差频组合, 考虑到实验中635 cm-1的强度和各可能组合峰的强度, 认为635 cm-1是319 cm-1的倍频。 面外扭曲形成两个振动峰, 一为由连接两Cl原子的C原子为主的面外扭曲形成, PED占86%, 具有中等红外强度, 拉曼强度很小, 与红外和拉曼实验吻合, 其峰位于762 cm-1处, 另外一个峰来自于两个碳原子和两氮原子整体的面外扭曲, 耦合有整个环的面外扭曲, 红外强度很小, 仅在KBr测量中出现, 其拉曼强度为8.38, 在Laser和FT-Raman中分别位于412和410 cm-1。

3.2.3 C-Cl振动

因Cl原子质量较大, 使与其相关的振动频率整体偏小, 对应的基频多处于远红外端, 中红外光谱中仅有CCl的一个反对称伸缩振动模式, 该波段红外实验均为一单峰, 附近也无其他峰干扰, 简振示意图和PED分析均支持上述归属。 Liquid、 KBr和Nujol测量其分别位于557、 554和559 cm-1, 非谐频率(544 cm-1)与实验值有~10 cm-1差异, 事实上, 非谐计算在高频端会降低振动频率, 使其与实验值更加吻合, 但在低频端往往会高估非谐效应, 其计算的频率值反而不及谐性近似下的估计值。 在其他几个CCl振动峰中也有所体现。 计算表明, 该振动的拉曼强度很小, 无论是激光还是傅里叶拉曼测量, 也确实未观测到该峰。 非谐计算显示CCl的对称伸缩振动峰位于346 cm-1, 具有最大的拉曼强度, 属A1对称。 Laser-Raman实验支持这一结果, FT-Raman中其强度与794 cm-1相近, 而谐性计算显示该峰在350 cm-1处, 与FT-Raman和Laser-Raman峰351和352 cm-1几乎一致。 CCl对称伸缩同时触发了整个嘧啶环面内剪切振动, PED分析显示两振动的贡献达90%, CCl的面内摇摆和面内剪切振动分别位于375和230 cm-1, 两者占简振振动的95%和91%, 319和88 cm-1为非常明显的CCl面外扭曲和面外摇摆振动。

3.3 同位素效应

为研究同位素效应引起的光谱变化, 对同位素取代后2, 5-DCP的振动光谱进行非谐计算。 计算中除同位素质量变化外, 其余参数与前完全一致, 这将排除掉因参数设置问题导致的计算结果差异, 得到取代后的24个基频, 结果见表5。 由于最丰同位素35Cl与37Cl的质量差异不大, 因此替代前后两者的基频差异很小, 均在10 cm-1以下甚至更小, 如: 35ClC的反对称伸缩振动为544 cm-1, 对应的37ClC峰在536 cm-1处。 最大的光谱差异来自于D替代产物, 这是由于H、 D质量相对变化大的原因, 如: 基频3 044 cm-1, D替代后转移到2 288 cm-1, 说明该振动峰主要由H的振动导致。 基于上述思想, 可以检验前文振动光谱的归属情况, 鉴于篇幅限制, 这里不再展开讨论。

表5 同位素取代后的非谐振动预期 Table 5 Predicted vibrational wavenumbers of substituted 2, 5-Dichloropymidine
4 结论

采用KBr压片法、 熔融法、 石蜡油法和衰减全反射法测定了2, 5-DCP的红外光谱, 同时收集了其傅里叶变换拉曼光谱和激光拉曼光谱。 利用多种密度泛函理论方法和多对基组对2, 5-DCP的振动光谱进行非谐计算, 优选出B3LYP方法和6-311++G(2df, 2pd)基组。 基于该组合计算的非谐振动频率和振动强度、 简振振动示意图、 势能分布, 结合实验红外和拉曼光谱, 对2, 5-DCP的振动光谱进行归属, 两个耦合效应被发现。 最后预测了同位素替代后的振动频率, 同时检验了本文光谱归属的合理性。

参考文献
[1] Norman J P, Larson N G, Entz E D, et al. J. Org. Chem. , 2022, 87(11): 7414. [本文引用:1]
[2] Alexand er J B, Paul T B, Hamish M, et al. J. Phys. Chem. , 1996, 100(30): 12280. [本文引用:1]
[3] Tran S B, Maxwell B D, Wu H, et al. J. Label. Compd. Radiopharm. , 2011, 54(13): 813. [本文引用:1]
[4] Cao K, Tran S B, Maxwell B D, et al. J. Label. Compd. Radiopharm. , 2012, 55(8): 300. [本文引用:1]
[5] Barone V, Puzzarini C. Annu. Rev. Phys. Chem. , 2023, 74(1): 29. [本文引用:1]
[6] Yu H, Ryosuke T, Nuwan D S, et al. J. Chem. Phys. , 2019, 151: 064104. [本文引用:1]
[7] Anna K K, Sand ra L. Phys. Chem. Chem. Phys. , 2022, 24: 28109. [本文引用:1]
[8] Kale E K, Peter R F, Gregory T P, et al. J. Chem. Phys. , 2022, 157: 084311. [本文引用:1]
[9] Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian-09, Revision D. 01, Gaussian Inc, Wallingford CT, 2013. [本文引用:1]
[10] Jamroz M H. Vibrational Energy Distribution Analysis VEDA 4, Warsaw, 2004. [本文引用:1]
[11] https://sdbs.db.aist.go.jp [本文引用:1]
[12] WENG Shi-fu, XU Yi-zhuang(翁诗甫, 徐怡庄). Analysis by Fourier Transform Infrared Spectroscopy(傅里叶变换红外光谱分析). Beijing: Chemical Industry Press(北京: 化学工业出版社), 2010. 291. [本文引用:1]