本实验以CFRP为基底, 结构如图1所示, 后续在基底上喷涂2层漆层, 分别为白漆(white)和底漆(primer), 它们的折射率在0~2 THz内均基本保持不变, 取值分别为2.35和2.27。 因为样品由树脂传递模塑成型工艺制作而成, 因此在CFRP表面还存在一个树脂层, 如图1所示。 当太赫兹脉冲E₀入射到待测样品, 不考虑多重反射时, 脉冲可以在各界面处发生反射, 得到E₁— E₃这三个反射脉冲, E₄是否存在取决于太赫兹入射点的位置与入射方向, 具体反射路径如图2所示。 当考虑多重反射时, 各个界面都会产生对应的多次反射, 如图中的虚线部分E_M所示。 各反射脉冲的光程与其时域位置存在对应关系, 多重反射脉冲E_M的部分分量可能出现在E₁— E₃之间。 对于薄涂层样件, 由于多重反射引起了回波重叠, 即E₂— E₃与E_M的部分分量波形叠加, 在时域波形里很难直接确定E₂— E₃的具体位置, 从而不能用飞行时间法来获得涂层厚度。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 CFRP结构图Fig.1 CFRP structure

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 多层结构的太赫兹传播路径Fig.2 THz propagation paths of multilayer

归因于CFRP的各向异性, CFRP涂层上最后采集的太赫兹反射信号存在差别, 具体如图3所示。 图3(a)为同一入射方向, 不同测量点的反射波形, 图3(b)为同一测量点, 不同入射方向的数据。 显然样件上不同位置、 不同方向的太赫兹反射信号存在明显差别。 而基于理论模型的优化算法求解涂层厚度时, 使用仿真信号与实际信号误差最小原则来确定厚度, 考虑到各向异性材料上的涂层反射信号具有多样性, 因此其精度有限。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 样件2不同情况下的太赫兹时域波形 (a): 不同测量点同一方向的THz波形; (b): 同一测量点不同方向的THz波形Fig.3 THz time-domain waveforms of sample 2 in different conditions (a): THz waveforms in the same direction at different measuring points; (b): THz waveforms in different directions at the same measuring point

事实上, 从理论分析与太赫兹反射信号的时域波形上看, 基底的各向异性只对反射信号后面的部分形状有影响, 前面部分的波形中已经含有E₁— E₃反射波形信息。 因此, 只要从前面波形里分解出E₁— E₃的信号, 就不用考虑基底的各向异性。 本文采用稀疏分解^[13]方法来解决薄涂层测厚所存在的问题, 定位E₁— E₃信号并使用TOF方法求取CFRP上的涂层厚度。

理论上, 多层结构的涂层作为一个物理系统, 太赫兹信号的传播路径只在分界面发生改变。 因此, 可将待测样品对太赫兹信号的响应近似看作线性系统。 则在时域上, 测量的反射信号可由入射信号与系统的脉冲响应函数卷积得到, 其数学形式为

y(t)=i(t)⊗h(t)+e(t) (1)

式(1)中, y(t)为太赫兹反射回波信号, i(t)为太赫兹入射信号, h(t)为样品的单位脉冲响应, ⊗为卷积符号, t为延迟时间, e(t)代表噪声。

太赫兹时域系统采集信号时遵循奈奎斯特-香农采样定理, 因此需要将连续卷积模型离散化, 离散卷积模型表示为

yn=∑k=0N-1in-khk+en (2)

式(2)中, y_n=y(nT_s), h_k=h(kT_s), n和k代表数据采样点的指数, T_s为采样周期, N是测量信号的长度。 实际情形下, 涂层的层数是有限的, 因此脉冲响应序列h中的大部分元素为0, 只有很少部分的非零值对应着各个涂层界面, 即脉冲响应函数是一个稀疏的序列, 将其写成矩阵形式

Y=Ah+e (3)

式(3)中, Y为N× 1维矩阵, A为N× N维矩阵, h为N× 1维矩阵。

由于h是稀疏的, 因此式(3)可看作信号Y的稀疏分解问题, 当Y和A为已知条件时, 通过式(4)可以求解稀疏向量h。

ĥ=arg minh‖h‖0 subject to ‖Y-Ah‖2≤ε (4)

式(4)中‖ h‖ ₀的求解属于NP-hard问题^[14]。 针对该问题的解决方法主要分为两大类: 第一种是求解该问题的一个近似解, 即通过不断迭代, 更新信号的支撑集, 达到逼近目标信号的目的, 该方法称为贪婪算法。 第二种是使用1范数代替0范数, 将NP-hard问题转换为一个近似问题求解, 即求解一个凸最优问题, 凸优化的模型如式(5)所示

ĥ=arg minh‖h‖1 subject to ‖Y-Ah‖2≤σ (5)

式(5)中, σ 是正则化参数, 用于平衡h的稀疏性和残余范数大小。

对于凸优化的求解方法, 正则化参数σ 非常重要, 平衡着信号重建精度与稀疏度, 它的选择与稀疏字典A的质量与信号噪声情况密切相关, 在实际使用中不易确定。 为此, 本文基于调参方便和充分利用先验知识的考虑, 选择使用能够指定稀疏脉冲个数的贪婪类算法。 贪婪算法中的代表性算法为1993年Mallat等^[15]提出的匹配追踪算法(matching pursuits, MP)和2007年Tropp和Gilbert^[16]提出的正交匹配追踪算法(orthogonal matching pursuits, OMP), 这两类算法均可用于信号稀疏表示与信号重构。 其中MP方法的方向选择是次优的, 因为残差只与当前投影方向垂直, 在后续投影中, 很可能会再次投影到原来的方向; 为此, OMP算法对所选择的全部原子正交化处理, 使得同一个原子不会被选择两次。 这两种算法都是基于局部最优策略, 并没有考虑所选原子对于最终迭代残差的影响。 为了将原子搜索从局部最优推广至全局最优, Chatterjee等提出了LAOMP算法^[17], 该算法加入了前向预测策略, 在每次迭代中先选择L个与残差内积最大的原子, 然后分别计算这L个原子在最终迭代中的性能, 最后选择使迭代残差最小的原子。 稀疏分解方法和飞行时间法结合, 实现CFRP基底上薄涂层厚度检测的整体流程图如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 稀疏分解法和飞行时间法测厚流程图Fig.4 Flow chart of thickness measurement by sparse decomposition and TOF method

实验采用Menlo System Tera K15全光纤式太赫兹时域光谱系统, 中心波长为1 560 nm, 探测频谱宽度为0.3~3 THz。 先在CFRP基底喷涂底漆, 干燥后再喷涂白漆, 制备了2个不同厚度的样件, 在样件切面用厚度仪测得油漆厚度, 具体厚度如表1所示。 在多个硅片上分别涂抹单层样漆, 采集太赫兹透射光谱, 再根据测量的厚度计算漆的折射率, white的折射率为2.35, primer的折射率为2.27。 CFRP涂层样品在正常的空气环境下, 采用反射的方式采集太赫兹信号, 太赫兹波的入射角度为35° 。

表1

Table 1

表1(Table 1)

表1 样件厚度设置 Table 1 Settings of sample thickness 样件 白漆/μ m 底漆/μ m 总厚度/μ m 样件1 30.48 35.56 66.04 样件2 66.04 35.56 101.6

表1 样件厚度设置 Table 1 Settings of sample thickness

CFRP的各向异性在光学特性方面表现为同一位置不同方向入射、 不同位置同一方向入射求得的复折射率均不同。 因此, 可以使用等效界面模型产生多层结构的太赫兹反射仿真信号, 通过改变基底的复折射率模拟各向异性特质, 从而验证测厚方法在理想情况下的有效性。

2.2.1 LAOMP算法验证

涂层厚度和折射率按样件2设置, 基底取不同厚度、 不同复折射率的THz反射仿真波形如图5所示。 LAOMP算法的稀疏度K设置为3, 对于图5中不同情况的厚度检测结果如表2所示, 其结果表明: 当涂层一样, 基底复折射率、 厚度发生变化时, LAOMP算法可准确实现对涂层厚度的检测, 并且一致性好。 白漆的厚度相对误差低于4%, 底漆的相对误差较大, 总厚度误差低于5%。 底漆误差较大的主要原因是白漆与底漆的折射率差别不明显且底漆相对较薄, 对应分界面的回波不明显。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同基底时的太赫兹时域波形Fig.5 THz time-domain waveforms of different substrates

表2

Table 2

表2(Table 2)

表2 不同基底时LAOMP算法的厚度检测结果 Table 2 The thickness result of different substrates by LAOMP 基底参数 d1/μ m d2/μ m d1+d2/μ m n=1.2, d=60 66.67 29.86 96.53 n=1.2, d=100 68.57 29.86 98.43 n=1.2, d=150 68.57 29.86 98.43 n=1.2, d=200 68.57 29.86 98.43 n=1.5, d=60 68.57 29.86 98.43 n=1.8, d=60 68.57 29.86 98.43 n=2.0, d=60 68.57 29.86 98.43 n=1.5, d=100 68.57 29.86 98.43 n=1.8, d=150 68.57 29.86 98.43 n=2.0, d=200 68.57 29.86 98.43

表2 不同基底时LAOMP算法的厚度检测结果 Table 2 The thickness result of different substrates by LAOMP

2.2.2 噪声鲁棒性分析

太赫兹时域系统在实际检测中会引入各类噪声, 尽管噪声产生的机理复杂, 但是可以近似采用高斯噪声、 脉冲噪声两者的组合表示。 在样件1、 2的仿真波形中加入0.2比例的高斯噪声和0.2比例的脉冲噪声, LAOMP算法的厚度检测结果如表3所示。 由表3可知, 无论是否加入噪声, LAOMP算法获得的单层和总厚度结果均接近于设定厚度值, 且结果稳定。 图6(a)为在样件2信号中加入噪声的波形, 图6(b)为LAOMP算法的稀疏分解效果。

表3

Table 3

表3(Table 3)

表3 LAOMP算法的厚度结果(μ m) Table 3 The result of thickness by LAOMP (μ m) 样件 厚度 设定值 LAOMP (K=3) 测量 总厚度 总厚度相对 误差/% 样件1 white 30.48 36.19 61.46 6.94 primer 35.56 25.27 white(noise) 30.48 30.48 60.34 8.63 primer(noise) 35.56 29.86 样件2 white 66.04 66.67 96.53 4.99 primer 35.56 29.86 white(noise) 66.04 66.67 96.53 4.99 primer(noise) 35.56 29.86

表3 LAOMP算法的厚度结果(μ m) Table 3 The result of thickness by LAOMP (μ m)

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 加入高斯噪声、 脉冲噪声的太赫兹时域波形和LAOMP算法重构的脉冲序列 (a): 加入高斯噪声、 脉冲噪声的信号; (b): 加入噪声后LAOMP算法重构的脉冲序列Fig.6 THz signal with gaussian, pulse noise and the reconstructed impulse response sequence by LAOMP (a): THz signal with gaussian, pulse noise; (b): The reconstructed impulse response sequence of noise signal by LAOMP

2.3.1 实测数据验证

实验室环境下测量的参考信号和样件2信号如图7所示, 考虑到实际操作过程中, 会因为技术、 环境等因素, 造成涂层不均匀, 因此, 在每个样件上选取20个不同位置的测量点, 采集20次数据, 利用算法获得20次数据的分解结果。 结合实际涂层折射率和多层涂层太赫兹反射信号理论模型的分析, 可知符合条件的稀疏脉冲规律应为正-负-负, 使用上述规律并选择绝对值最大脉冲来定位分界面。 因为实际测量数据会受到多种因素的影响, 并不是每一个实际数据都可以分解获得符合稀疏脉冲规律的结果。 同时, 考虑到实际使用中, 对于同一个样件的多个测量信号, 更希望采用相同的参数设置。 因此, 在设置相同参数的情况下, 获得的符合稀疏脉冲规律的结果称为有效分解。 LAOMP算法获得的有效分解次数和厚度结果如表4所示, 表中的单涂层以及总厚度数据均为有效分解数据的均值。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 实验室环境下的参考信号和样品信号Fig.7 Reference and sample signal in laboratory environment

从表4中的结果可知: LAOMP算法可以有效检测薄涂层, 总厚度误差控制在11%以内。 误差相对较大, 主要原因为实验中的两层涂层均为较小厚度, 折射率相差不大, 使得两层漆的分界面较难区分。 同时, 在样件的制备过程中还存在涂层不均的情况, 切口所测的漆厚度与各点实际厚度的平均值存在误差。

表4

Table 4

表4(Table 4)

表4 LAOMP方法的厚度结果 Table 4 Thickness results of the LAOMP methods 方法 实验次数 有效分解 次数 白漆 /μ m 底漆 /μ m 总厚度 /μ m 实际总厚度 /μ m 相对误差 /% 样件1 LAOMP 20 8 29.05 29.86 58.91 66.04 10.79 样件2 LAOMP 20 9 54.81 36.50 91.32 101.60 10.12

表4 LAOMP方法的厚度结果 Table 4 Thickness results of the LAOMP methods

2.3.2 与SPGL1算法对比

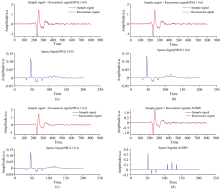
为了对比凸优化算法在本实验中的检测效果, 选择了SPGL1算法。 对于样件1组, SPGL1算法的实现效果如图8所示, 图8(a)、 (b)、 (c)分别为参数σ 设置0.8、 0.6和0.4时的重建和稀疏脉冲情况, 当参数σ 设置的越小, 信号的重建效果越好, 符合理论, 但是这几个参数对应获得的尖峰周围都存在明显波动, 直接影响后续飞行时间法的使用。 图8(d)为LAOMP算法在样件1组的处理结果, 无论是重建效果还是尖峰周围的稳定性, 均更适合用于涂层界面的分析。 对于样件2, SPGL1算法同样难以满足信号重建精度和脉冲稳定性, 而LAOMP算法可以同时实现。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 SPGL1和LAOMP算法在样件1上的结果 (a): SPGL1参数为0.8的结果; (b): SPGL1参数为0.6的结果; (c): SPGL1参数为0.4的结果; (d): LAOMP的结果Fig.8 The result of sample 1 by SPGL1 and LAOMP (a): The result of parameter 0.8 in SPGL1; (b): The result of parameter 0.6 in SPGL1; (c): The result of parameter 0.4 in SPGL1; (d): The result by LAOMP