为了研究该吸波材料反射特性, 获得更宽的频谱特性, 我们通过三套不同系统测量了吸波材料板的反射率。 有效的覆盖了微波、 太赫兹、 红外波段。 三种测量系统分别是基于矢量网络分析的微波暗室测量系统、 太赫兹时域光谱系统、 傅里叶变换光谱系统。 其中, 基于矢量网络分析仪的暗室测量频段可覆盖1 GHz~40 GHz, 而太赫兹时域光谱系统和傅里叶变换光谱都能覆盖一部分太赫兹频段, 其中太赫兹时域光谱系统在太赫兹低频段有着较好的信噪比, 在太赫兹高频(2~10 THz)以及红外波段, 傅里叶变换光谱仪更具测量优势^{[4, 5, 6]}。

1.1.1 微波段实验测量系统

在1~40 GHz波段内, 吸波涂层样件反射率测量采用雷达散射截面(RCS)测量方法, 电磁波从同一方向, 以同一功率密度入射到雷达吸波涂层和定标良导体平面, 如图1所示。 实验室测量系统以罗德施瓦茨生产的ZVA40型矢量网络分析仪(10 MHz~40 GHz)为基础构成, 主要包括发射机(E)和接收机(R)、 主反射面(M₁)、 副反射面(M₂)。 测量过程中, 电磁波会覆盖整个吸波涂层, 得到吸波涂层样件随频率变化的回波功率P_s(f), 再需要获得参考良导体随频率变化的回波功率P_c(f), 从而获得反射率

R=PsfPcf(1)

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 微波暗室测量反射率测量示意图 E: 发射天线; R: 接受天线; M1, M2: 反射面; 样品板放置于泡沫台体(白色)上Fig.1 Schematic diagram of reflectivity measurement in a microwave anechoic chamber E: The transmitting antenna; R: The receiving antenna, M1, M2: The reflecting surfaces; The sample plate is placed on the foam table (white)

1.1.2 太赫兹时域光谱的反射率测量系统(太赫兹低频部分)

太赫兹时域光谱技术的反射率测量系统如图2所示, 该太赫兹系统为美国API公司生产的T-ray 5000型光纤耦合式的太赫兹时域光谱仪, 频谱分辨率1.5 GHz, 动态范围达到80 dB, 有效工作频率覆盖0.05~2 THz。 为了保证系统能够实现多角度的反射测量制作了一个半圆形轨道框架, 框架由一个长方形外框架和内置半圆形轨道组成, 顶端放置了一个角度可调的样品支架。 外框架用有机玻璃板进行封闭, 使得系统具有一定的气密性, 测量样品材料时通过给框架内填充干燥空气, 排除测试区内的水分, 减少大气环境对太赫兹的吸收。 测量时顶端处放置参考板, 太赫兹频段的材料测量采用镀金反射镜作为参考, 获得反射功率P_ref; 撤去镀金反射镜, 换上样品, 获得样品的反射功率P_sam, 两次测量通过样品架对参考板和样品材料板的前表面进行限位, 利用样品和参考板的自身重力使其前表面紧密接触到样品架, 最大程度避免前表面放置误差给反射测量带来的影响。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 太赫兹时域光谱系统Fig.2 Terahertz time-domain spectroscopy

1.1.3 太赫兹时域光谱的反射率测量系统(太赫兹低频部分)

红外波段采用Bruker公司生产的Vertex-80v型真空傅里叶变换光谱仪进行了太赫兹高频段模块(2~20 THz)和红外波段模块(20~180 THz)绝对反射率测量。 如图3所示, 先进行参考板反射能量的测量, 该测量中太赫兹只经过一次镀金反射镜的反射; 第二步进行样品测量, 该测量中太赫兹波先后两次经过样品反射, 其间经历一次参考镀金反射镜的反射; 用样品信号除以参考信号, 可消除参考镜子反射率不为1的影响, 获得样品的绝对反射率。 由于太赫兹、 红外波段, 测量容易受到水汽和二氧化碳气体的吸收影响, 测量时系统内做抽真空处理。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 绝对反射装置示意图Fig.3 Schematic diagram of absolute reflection device

R(ν)=PsamPref=R1(ν)RM(ν)R2(ν)RM(ν)=R1(ν)R2(ν)=R2(ν)(2)

式(2)中, R_M为参考镀金反射镜的反射率, R₁(ν )和R₂(ν )分别为反射第一次经过样品和第二次经过样品的反射率。

1号样品: 使用传统磁损耗型吸收剂羰基铁粉, 加入环氧树脂、 促进剂D、 二甲苯和丙酮等, 搅拌使其溶解并混合均匀, 得到吸波涂料, 以铝合金板为基板进行喷涂, 喷涂完成后得到吸波涂层, 涂层厚度0.5 mm。 2号样品: 用球磨机研磨二氧化硅粉和羰基铁粉混合物, 加入氯磺化聚乙烯橡胶、 松香和环氧树脂等, 搅拌得到的吸波涂料喷涂到铝合金板, 涂层厚度0.5 mm, 两块样品如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 1号(左)和2号(右)吸波材料板样品Fig.4 Sample of absorbing material plate No.1 (left) and No.2 (right)

测量获得1~40 GHz波段内两个样品反射率如图5所示。 1号样品反射率在1~6 GHz表现为单调下降到R≈ 0.3, 随着频率进一步升高, 反射率也逐步提升, 吸波性能随之下降, 该涂层表现出典型的窄波段吸波性能。 在1~6 GHz频段内, 2号样品的反射率略微高于1号样品。 但是在7~37 GHz频段内, 2号样品反射率R< 0.4, 表现出良好的宽波段吸波能力, 甚至在33 GHz处有共振吸收点, 使得该频率处反射率R≈ 0.15。 当频率达到在40 GHz时, 2号样品的反射率上升至约0.7, 与1号样品吸收能力相当。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 样品1~40 GHz频段范围的反射率, 频率采样间隔0.04 GHzFig.5 Reflectance of sample in the 1 to 40 GHz frequency range, with a frequency sampling interval of 0.04 GHz

由于太赫兹时域光谱产生的太赫兹光斑直径约为5 mm, 不能一次性覆盖整个涂层平板, 因此在该样品上选择了三个位置(标记为P₁、 P₂和P₃)作为采样位置。 时域太赫兹波以入射角θ =15° 照射1号样品三个位置, 其反射率测量结果如图6(a)所示, 涂层喷涂不均导致了三个位置的反射率存在差异。 在0.6~1 THz范围, P₁和P₃处反射率接近, 而在1~1.8 THz范围, P₁和P₂差异较小, 这表明不同频率的反射率反映了吸波涂层色散特性。 在0.2 THz频点处三个位置反射率平均值约为R≈ 0.6, 与40 GHz频点处的反射率R≈ 0.65较为接近, 这表明1号样品从微波到太赫兹低频段(小于2 THz)反射率曲线随频率变化表现的较为平缓, 表明1号吸波涂层样品在太赫兹低频区间[0.1 THz, 2 THz]吸波能力较差。 利用TDS测量2号样品在0.2~2 THz反射率表现出随频率升高而下降行为如图6(b)所示, 在0.2 THz频点处反射率平均值约为R≈ 0.5, 参照40 GHz处反射率R≈ 0.7, 说明从微波到太赫兹低频段反射率曲线呈现下降趋势。 2号样品在2 THz处, 反射率下降到R≈ 0.1左右, 表明这2号样品在[0.1 THz, 2 THz]频率区间具有良好的吸波能力。 尽管三处位置的反射率对频率依赖趋势一致, 但是其细节差别明显, 来源于金属衬底上涂层厚薄的不均匀性。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 材料板在[0.1, 2]THz反射率随频率的变化关系 (a): 1号样品(No.1)上三个不同区域的测量结果; (b): 2号样品(No.2)在三个不同区域的测量结果Fig.6 Frequency dependence of reflectivity of material plates at [0.1, 2] THz (a): The measurement results of sample No.1 in three different areas; (b): The measurement results of sample No.2 in three different areas

我们测量了不同的入射角(15° < θ < 60° )下0.1~2 THz的材料板P₁处的反射率, 测量结果如图7所示, 两种材料样品的反射率随着入射角增大, 反射率逐渐变小, 这与菲涅耳公式计算的趋势一致。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同入射角反射率 (a): 1号样品; (b): 2号样品Fig.7 Reflectivity at different incident angles (a): Sample 1; (b): Sample 2

对于太赫兹高频段部分, 使用太赫兹波段测量探测器(DTGS晶体), 入射角度为θ =15° 时, 1号样品在三个不同位置的反射率测量结果如图8(a)所示。 在太兹高频段, 1号样品的三个位置反射率都随频率增加而单调下降, 且三个位置反射率差异性更为显著和稳定, 表明高频太赫兹波能有效检测出该样品吸波涂层不均特性。 当频率增加至红外波段时, 反射率继续下降至10^-2左右, 反射率曲线开始出现明显的振荡行为, 如图8(b)所示。 三个测量位置的振荡行为开始频率略有不同, 可能来源于涂层不同测量位置表面粗糙度略有差别, 但是当频率超过120 THz后, 三个位置粗糙程度对该频段的电磁波说都足够粗糙, 所以三个位置的反射率振荡行为较为类似。 2号材料的太赫兹高频段部分反射率如图8(c)所示, 反射率随频率表现为准周期(大约为4 THz)变化行为, 该行为是由于太赫兹波反射干涉叠加现象, 与涂层表面厚度不均匀有关。 当频率进一步增加至红外波段时, 多次反射干涉叠加现象依然存在, 如图8(d)所示。

图8

Fig.8

Figure Option ViewDownloadNew Window

图8 样品在太赫兹、 红外频段的反射率测量结果 (a): 1号样品在太赫兹高频段反射率, 其采样间隔0.015 THz; (b): 1号样品在红外波段的反射率, 采样间隔0.23 THz; (c): 2号样品在太赫兹高频段的反射率; (d): 2号样品在红外波段的反射率Fig.8 Reflectance measurement results of the sample in the terahertz and infrared frequency bands (a): Reflectance of sample 1 in the terahertz high-frequency range, with a sampling interval of 0.015 THz; (b): The reflectance of sample 1 in the infrared band, with a sampling interval of 0.23 THz; (c): The reflectivity of sample 2 in the terahertz high frequency range; (d): Reflectance of sample 2 in the infrared band

对于不同的入射角(15° < θ < 60° ), 太赫兹高频段和红外波段内, 1号样品的反射率都满足随频率提高而单调下降关系, 如图9(a)和(b)所示; 而2号样品反射率随频率准周期变化行为依然存在, 如图9(c)和(d)所示。 尽管不同入射角的反射率数值定量存在差异, 但是反射率随频率变化的行为特征较为一致, 也反映不同角度下吸波涂层稳定的吸波能力。

图9

Fig.9

Figure Option ViewDownloadNew Window

图9 反射率随角度频率的变化关系 一号样品在(a)太赫兹高频段部分和(b)红外频段反射率随频率、 角度变化的测量结果; 二号样品在(c)太赫兹高频段部分和(d)红外频段反射率随频率、 角度变化的测量结果Fig.9 The variation of reflectivity with angle and frequency The measurement results of the reflectivity of sample 1 in the (a) terahertz high-frequency band and (b) infrared frequency band as a function of frequency and angle; The measurement results of the reflectivity of sample 2 in the (c) terahertz high-frequency band and (d) infrared frequency band as a function of frequency and angle

为了更好的理解该吸波材料的特性, 我们将该吸波材料涂覆层从金属衬板上剥离, 对涂覆层在太赫兹的中高频段及红外段的反射率、 透射率进行了测量, 如图10所示, 并反演了其等效介电参数, 如图11, 此处材料参数反演所用的反射率区别于前面工程应用领域的雷达吸波材料板的反射率, 测量吸波材料样品时反射不再放置金属衬板。 材料参数的反演利用了Kamers-Kronigs关系^{[7, 8, 9, 10, 11]}给出的反射率的振幅R(ω )和相移θ (ω )之间的表达式

θ(ω)=ωπ∫0∞lnR(ω')-lnR(ω)ω2-ω'2dω'(3)

式(3)中, 积分范围为[0, ∞ ], 而实际测量频率测量范围为有限范围[ω ₁, ω ₂], 需要在高频段和低频段进行外推的近似处理^[4]。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 材料层的透射率和镜向反射率 (a): 1号样品涂层在太赫兹红外的透、 反射率; (b): 2号样品涂层在太赫兹红外的透、 反射率Fig.10 Transmittance and mirror reflectance of material coating (a): The transmittance and reflectance of coating No.1 in THz and infrared; (b): The transmittance and reflectance of coating No.2 in THz and infrared

图11

Fig.11

	Figure Option ViewDownloadNew Window
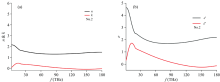
	图11 1号材料涂层材料参数 (a): 1号涂层材料的等效复折射率; (b): 1号涂层材料的等效介电参数Fig.11 Dielectric parameters of No.1 material coating (a): The complex refractive index of coating No.1; (b): The permittivity of coating No.1

根据相位和反射率的关系计算出折射率n(ω )、 消光系数k(ω ), 从而计算出介电常数实部ε _r、 虚部ε _i。

n(ω)=1-R2(ω)R2(ω)-2R(ω)cosθ+1(4)

k(ω)=2R(ω)sinθ(ω)R2(ω)-2R(ω)cosθ(ω)+1(5)

εr=n2(ω)-k2(ω)(6)

εi=2n(ω)k(ω)(7)

反射率材料参数计算结果如图11所示, 从材料层自身的透、 反射率来看, 太赫兹、 红外几乎是无法有效地穿透该厚度的吸波涂层到达金属衬板, 材料对太赫兹、 红外的吸收主要发生在反射界面处, 趋肤深度内, 同时受微波材料表面粗糙影响, 非镜向散射也是导致反射率不高的一个因素。 从两块材料板涂层的等效介电参数来看, 在太赫兹频段及远红外频段(2~20 THz), 其消光系数大于1, 这代表着样品的吸收较强。 在中红外段, 材料的折射率和消光系数均逐渐变小。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 2号材料涂层等效材料参数 (a): 2号涂层材料的等效复折射率; (b): 2号涂层材料的等效介电参数Fig.12 Dielectric parameters of No.2 material coating (a): The complex refractive index of coating No.2; (b): The permittivity of coating No.2