引用本文
唐维鑫, 丁涛, 李东鲜, 张昌华, 李萍. 高速冲击波下的高温空气辐射光谱研究[J]. 光谱学与光谱分析, 2024,44(10): 2739-2744.
TANG Wei-xin, DING Tao, LI Dong-xian, ZHANG Chang-hua, LI Ping. Study of High-Temperature Air Radiation Spectrum Under High-Speed Shock Wave[J]. Spectroscopy and Spectral Analysis, 2024,44(10): 2739-2744.
Doi:10.3964/j.issn.1000-0593(2024)10-2739-06  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
高速冲击波下的高温空气辐射光谱研究
唐维鑫, 丁涛, 李东鲜, 张昌华*, 李萍
四川大学原子与分子物理研究所, 四川 成都 610065
*通讯作者 e-mail: zhangchanghua@scu.edu.cn

作者简介: 唐维鑫, 1999年生,四川大学原子与分子物理研究所硕士研究生 e-mail: townwesssn123@163.com

收稿日期: 2023-03-29 修回日期: 2024-01-12
基金: 国家自然科学基金重大研究计划基金项目(91841301)资助
摘要

飞行器再入地球大气层过程中, 高速飞行器头部的温度可达到10 000 K以上导致飞行器气动性能的变化。 空气的辐射加热是飞行器表面传热的主要来源之一, 对高速冲击波下的空气辐射光谱进行测量研究, 是研究超高速飞行器飞行过程中辐射效应和动力学行为的重要基础。 目前高温空气辐射光谱的测量数据依旧较少, 还需要大量的实验数据对计算模型进行改进优化。 利用氢氧爆轰激波管结合瞬态光谱测量系统获得了速度在3 259~8 218 m·s-1下高温空气在紫外-可见区的辐射光谱, 并对典型高温空气辐射光谱进行了特征光谱的光谱识别和模拟, 模拟结果和实验结果吻合较好, 验证了光谱识别的准确性和可靠性; 同时探究了激波速度对于高温空气辐射特性的影响, 并对特征光谱进行了动力学行为分析。 结果表明, 在波长225~675 nm范围内, 特征光谱主要存在于波长小于500 nm的区域; 不同速度下的辐射光谱中存在不同的特征光谱, 通过光谱识别后发现随着激波速度的增加, 先后出现OH(A-X)、 NO(γ, ε, δ)、 NH(A-X)、 N2(C-B)、N2+(B-X)和Hα等特征光谱, 获得了辐射特性随激波速度的变化情况。 还根据辐射光强度随时间变化曲线获得了波后空气激发的弛豫时间, 随着速度的增加, 弛豫时间在逐渐缩短, 与速度近似呈现指数关系。 研究了激波速度对高温空气辐射特性的影响, 研究结果为飞行器热防护设计和超高声速再入大气层过程的计算模型的验证优化提供实验数据和参考。

关键词: 高温空气; 辐射光谱; 弛豫时间; 激波管; 动力学分析
中图分类号:O433.1 文献标志码:A
Study of High-Temperature Air Radiation Spectrum Under High-Speed Shock Wave
TANG Wei-xin, DING Tao, LI Dong-xian, ZHANG Chang-hua*, LI Ping
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
*Corresponding author
Abstract

During spacecraft reentry into Earth's atmosphere, the temperature of the high-speed air at the front of the spacecraft can reach over 10 000 K, leading to changes in the aerodynamic performance of the spacecraft. Radiative heating is one of the main sources of surface heat transfer for spacecraft, and measuring the radiation spectra of air under high-speed shock waves is crucial for studying radiation effects and dynamic behavior during the flight of hypersonic vehicles. There is still a lack of measurement data for high-temperature air radiation spectra, and a large amount of experimental data is required to improve and optimize computational models. This paper uses a hydrogen-oxygen detonation shock tubecombined with a transient spectroscopic measurement system to obtain the radiation spectra of high-temperature air in the ultraviolet-visible region at velocities ranging from 3 259~8 218 m·s-1. The identification and simulation of typical high-temperature air radiation spectra characteristic spectra were carried out. The simulation results were in good agreement with the experimental results, validating the accuracy and reliability of the spectral identification. The impact of shock wave velocity on the radiation characteristics of high-temperature air was also analyzed, and the dynamic behavior of characteristic spectra was analyzed. The results showed that characteristic spectra mainly exist in the 225~675 nm wavelength range and the region with wavelengths below 500 nm. Different characteristic spectra were observed in the radiation spectra at different velocities. With increasing shock wave velocity, OH(A-X), NO(γ, ε, δ), NH(A-X), N2(C-B),N2+(B-X), and Hα spectral lines appeared successively. The relative intensities of the characteristic spectra vary with shock wave velocity. Finally, the relaxation time of post-shock air excitation was determined based on the time-varying curve of radiation intensity. The relaxation time gradually shortened with increasing velocity and exhibited an exponential relationship with velocity. This study provides experimental data and references for spacecraft thermal protection design and the validation and optimization of computational models for hypersonic reentry into the atmosphere.

Keyword: High-temperature air; Radiation spectrum; Relaxation time; Shock tube; Kinetic analysis
引言

高速飞行器再入大气层的过程中, 飞行器头部会形成激波层, 激波层会压缩并加热空气, 导致局部热辐射强度迅速增加。 此时空气温度可达到10 000 K以上使得飞行器表面发生烧蚀, 并对飞行器表面的热防护设计提出了挑战[1]。 同时, 飞行器以极高的速度进入/再入大气层时, 氮分子离解产生的氮原子会发生复合反应放出大量的热, 使飞行器表面的热载荷进一步上升[2]。 高温不仅会改变激波的位置和形状, 还会改变边界层的特性, 对飞行器的流动结构气动性能影响显著, 最终导致飞行器气动性能的变化[3]。

地面试验是探究高温气体效应的重要途径, 激波管能模拟高速激波下的高空环境, 是开展高温气体动力学研究的理想设备之一。 高温气体辐射光谱测量可以对气体动力学研究以及数值计算模型的构建优化提供实验依据, 还对飞行器在高速飞行过程的目标识别和气动光学效应具有重要的意义。 美国NASA Ames研究中心利用电弧驱动激波管开展了大量行星的再入飞行高温气体辐射实验[4, 5], 之后在此基础上进行了高速飞行再入过程中气体的动力学模型和辐射模型的建模和验证[6, 7]。 日本JAXA通过测量高温空气辐射的紫外区域光谱, 利用辐射光谱的数据对空气辐射模型进行构建[8], 此外他们还针对火星气体辐射特性进行了测量研究并构建了N2-CO2的高温辐射模型[9, 10]。 俄罗斯莫斯科国立大学利用爆轰驱动激波管开展了高温空气辐射的测量实验[11, 12]。 在国内, 中国科学院力学研究所采用激波管和发射光谱测量技术, 针对典型地球和火星再入条件下的辐射强度进行了测量实验和模型计算[13, 14]。 然而, 对于高速冲击下的动力学和辐射模型还有待进一步完善。 如NASA开发的NEQAIR等模型对于预测高温空气辐射光谱虽然一些情况吻合的比较好, 但是在多数工况下依旧存在偏差, 甚至偏差高达50%[5]; 日本JAXA构建的辐射模型在实验光谱和预测值也有部分差距[15]。 到目前为止, 对于高温空气辐射光谱的实验测量数据还比较少, 而对模型的优化改进需要大量的高温气体实验数据, 因此仍需要大量可靠的实验数据对相关计算模型验证支撑。

本文利用氢氧爆轰激波管结合瞬态光谱测量系统获得了紫外-可见区的高温空气辐射光谱, 对宽激波速度范围下的空气辐射进行了特征光谱和辐射特性的研究, 能进一步了解激波速度对于高温空气辐射特性的影响, 并为超高速飞行器热防护系统设计和飞行器超高速再入过程相关计算模型的开发改进提供了参考和实验数据。

1 实验部分

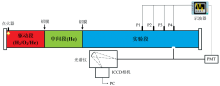
高温空气辐射光谱测量实验主要由氢氧爆轰驱动激波管和光谱测量系统组成, 实验装置如图1所示。 激波管直径为10 cm, 由驱动段、 中间段和实验段组成, 其长度分别为2、 2和6.2 m。 每段均配置独立的压力表用于检测气体压力, 各段之间通过刻有十字刻痕的铝膜片隔开。 驱动段充入H2/O2/He(混合气体摩尔比例为2∶ 1∶ 3)混合气体, 中间段加入氦气; 实验段气体为摩尔含量79%N2和21%O2的混合气体, 初始压力为200 Pa。 点火器安装在驱动段靠近端面处, 通过驱动段氢氧爆轰破膜的方式产生激波, 激波速度可以通过调节缓冲段和高压段的气体压力进行控制。 实验段沿轴向方向安装了四个间距20 cm的压电式压力传感器P1— P4(PCB 113B)用于监测激波信号, 传感器响应时间小于1 μ s, 根据四个压力传感器之间的距离和激波经过四个传感器的时间间隔用拟合法得到激波速度, 激波速度的不确定度小于0.6%。

图1 实验设备示意图Fig.1 Schematic diagram of the experimental setup

实验段最后一个压力传感器P4距端面1 m, 在P4同一截面安装了两个蓝宝石光学测量窗口, 采用两束紫外光纤将光信号分别导入ICCD光谱测量系统和光电倍增管(PMT), 一个用作采集激波波后高温空气在紫外-可见区的瞬态辐射光谱, 另一个用来监测高温空气辐射强度随时间变化的曲线。 光谱测量系统由光谱仪(Andor SR193i)和ICCD相机(Andor iStar)组成。 光谱仪焦距193 mm, 光栅刻线为150 l· mm-1, 测量范围为225~675 nm, 整个光谱测量系统分辨率为1.5 nm。 ICCD相机的像素数为1 024× 1 024, 曝光时间设置为1 μ s。 为了保证实验中光谱测量系统的可靠性, 每次实验之前对整个光学采集系统校准, 利用汞灯光源进行波长标定; 已标定的标准氘灯光源进行相对强度标定。 实验测量中, 利用压力传感器P4的压力信号触发ICCD光谱采集系统。 压力信号、 PMT信号和ICCD曝光快门信号在示波器中记录。

2 结果与讨论
2.1 特征光谱的识别

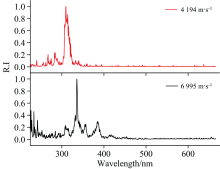
本文得到了激波速度范围在3 259~8 218 m· s-1的高温空气辐射光谱, 典型实验光谱如图2所示, 结果表明, 在所测量的紫外-可见光谱区中, 空气辐射光谱的特征光谱主要在225~500 nm范围, 因此在后面所展示的实验辐射光谱结果仅展示波长范围为225~500 nm。

图2 典型实验光谱Fig.2 Typical experimental spectra

图3展示了激波速度为4 194 m· s-1的空气辐射光谱和利用Specair软件进行OH(A-X)特征光谱(283, 309 nm)模拟的结果图。 模拟光谱是根据实验辐射光谱中特征光谱的相对强度对不同模拟特征光谱的相对强度归一化, 最后对所有模拟特征光谱叠加得到。 图3中的模拟温度为4 500 K, 实验辐射光谱和OH(A-X)模拟结果在275~325 nm范围基本吻合。

图3 激波速度为4 194 m· s-1的辐射光谱及模拟结果Fig.3 Radiation spectra and simulation results at a shock wave velocity of 4 194 m· s-1

图4为激波速度8 218 m· s-1的辐射光谱测量结果和模拟光谱结果, 因为本实验采用的瞬态实验光谱方法, 曝光时间短(~1 μ s)导致信噪比低难以对光谱的精细结构进行准确的模拟拟合。 对光谱中的特征光谱进行识别辨认, 发现模拟温度为6 000 K时和实验辐射光谱吻合较好, 结果表明该条件下主要有NO(γ , δ , ε ), N2(C-B), N2+(B-X), NH(A-X)的特征光谱, 其中NO(γ , δ , ε )为225~290 nm范围存在的特征光谱, N2+(B-X)特征光谱在388和422 nm具有明显谱线强度, 特征光谱NH(A-X)在336 nm有非常尖锐的峰。 表1中列出了本文测量得到的主要特征光谱及其波长。

图4 激波速度为8 218 m· s-1的辐射光谱及模拟结果Fig.4 Radiation spectra and simulation results at a shock wave velocity of 8 218 m· s-1

表1 高温空气辐射光谱中的特征光谱 Table 1 Characteristic spectra in high-temperature air radiation spectra
2.2 激波速度对高温空气辐射特性的影响

图5展示了对光谱强度归一化后激波速度在3 259~8 218 m· s-1范围内的高温空气辐射光谱。 在激波速度低于4 194 m· s-1时, 图5(a)和(b)中的空气辐射光谱在283和309 nm处出现非常明显的OH(A-X)特征光谱, 且速度低于4 194 m· s-1的时候只存在OH(A-X)特征光谱。 因为激波管实验段管壁内部会吸附微量H2O分子, 在激波波后的高温环境下, H2O分子热解为OH自由基和H原子, 在H2O分子的解离过程中可能会直接产生激发态OH(A)。 同时O2分子高温下解离出O原子, H2O分子与O原子发生反应生成激发态OH, H2O+O→ OH(A)+OH(X)[16]。 之后OH自由基发生A-X跃迁发出283和309 nm的光辐射。

图5 在不同激波速度下的高温空气辐射光谱Fig.5 High-temperature air radiation spectra at different shock wave velocities

激波速度到5 008 m· s-1时, 图5(c)中出现了NO(γ , ε , δ )特征光谱和NH(A-X)特征光谱。 NH(A-X)特征光谱的产生是因为实验段中H2O分子解离产生H原子, H原子与N2分子发生反应生成NH自由基, H+N2→ NH(A)+N[17], 随后NH(A)向低能级NH(X)跃迁出现NH(A-X)特征光谱; NO分子产生的主要来源是因为N2和O2分子与其他粒子(如N2, O2等)碰撞后解离为O原子和N原子, 而O原子和N2分子发生吸热反应生成NO分子, N2+O → NO+N; N原子和O2分子的放热反应生成NO分子, N+O2→ NO+O[18]。 NO(X2Π )分子激发至高能级的NO(A, B, C, D)后会发生NO(γ , β , δ , ε )能级跃迁, 但是由于激发态NO(A)、 NO(C)和NO(D)的存在时间很短, 所以NO相关辐射的主要光谱强度贡献来自于NO(γ , ε , δ )[19]。 在激波速度5 008 m· s-1的高温辐射光谱的OH(A-X)特征光谱的相对强度最大。

在图5(c)— (e)中显示随着激波速度增加, NO(γ , ε , δ )特征光谱和NH(A-X)特征光谱的相对强度逐渐增强。 在激波速度增加到5 735 m· s-1时, NH(A-X)特征光谱在336 nm处的相对强度最强, 如图5(e)所示。 在图5(f)中激波速度继续增加到6 240 m· s-1时, 辐射光谱388和422 nm处出现 N2+(B-X)的特征光谱。 这是由于N原子之间发生缔合电离反应生成 N2+离子, N+N→ N2++e- [18]。 之后随着激波速度增加, 图5[(f)-(l)]中 N2+(B-X)特征光谱的相对强度逐渐增强。 然而在激波速度7 686 m· s-1之后, N2+(B-X)特征光谱在辐射光谱中的相对强度不再增强。 Wang等[20]通过建立真实气体模型计算了纯净空气中各种粒子数密度随着温度变化曲线, 其中 N2+离子在温度超过5 530 K时出现, 随着温度的升高 N2+离子的数密度逐渐增加并在温度7 600 K达到最大, 该计算结果与本实验获得的 N2+(1-)谱峰的相对强度随激波速度的变化趋势相符合。

在图5(m)速度为8218 m· s-1的高温空气辐射光谱中, 656 nm处出现了Hα 特征光谱。 由于激波速度进一步升高导致温度升高, H2O分子的解离度越来越高, 同时OH自由基与其他粒子碰撞发生解离也会生成H原子, OH+M→ H+O+M, 这些原因会导致H原子数量增大。 在高温下的H原子激发至高能级n=3, 随后在电子态n=3向n=2的低能态跃迁并辐射出H原子特征光谱[21]。

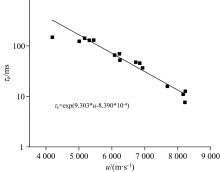
本文还测量了激波波后高温空气辐射强度随时间变化曲线, 典型结果如图6所示。 在激波波后空气辐射强度迅速增强, 然后逐渐减弱并最终到达平衡状态。 这种辐射强度的变化曲线反映了高温空气从非平衡状态到平衡状态的弛豫过程, 对应的时间即弛豫时间τ e。 在本文中, 定义弛豫时间τ e为高温辐射光强上升到最大强度10%的时刻至光强下降到斜率变化最大的时刻, 两者之间的时间间隔为弛豫时间τ e。 实验获得了不同激波速度下的高温空气的弛豫时间, 结果见图7所示。 弛豫时间τ e和速度u关系近似为指数关系, 拟合曲线拟合公式为: τ e=exp(9.303× u-8.389 77× e-4), 其中u为激波速度。 发现随着激波速度的增加, 弛豫时间也在逐渐减少, 这是因为激波速度u与温度T呈正相关关系, 即激波速度u越高波后温度T也越高, 温度T的上升导致气体分子的碰撞频率增加, 能量传递得更快, 因而分子更快的到达平衡状态, 弛豫时间减少。

图6 激波速度6 393 m· s-1的波后高温空气辐射强度随时间变化剖图Fig.6 Profile of the evolution of high-temperature air radiation intensity behind a shock wave with a velocity of 6 393 m· s-1 as a function of time

图7 弛豫时间和激波速度的关系Fig.7 Relationship between relaxation time and shock wave velocity

3 结论

利用氢氧爆轰激波管结合瞬态光谱系统测量了紫外-可见区(225~675 nm)、 激波速度为3 259~8 218 m· s-1的高温空气辐射光谱。 通过模拟结果和典型辐射光谱的对比, 对高温空气辐射光谱的特征光谱进行了识别, 同时探究了激波速度对于高温空气的辐射特性的影响。

在测量范围内, 特征光谱大多在波长小于500 nm的区域, 通过光谱模拟发现高温空气辐射中存在NO(γ , ε , δ ), OH(A-X), NH(A-X), N2(C-B), N2+(B-X)和Hα 特征光谱。

通过比较不同激波速度的高温空气辐射光谱, 研究了激波速度对辐射特性的影响。 发现在激波速度低于4 194 m· s-1的光谱中, 仅存在OH(A-X)的特征光谱; 随着速度的增加, 先后出现了NO(γ , ε , δ ), NH(A-X), N2(C-B), N2+(B-X)和Hα 的特征光谱。 经动力学分析, OH(A-X)和Hα 特征光谱的出现是由于激波管内壁附着的微量H2O分子解离导致的; H原子和N2分子发生复合反应导致NH(A-X)特征光谱; N2分子和O2分子在碰撞解离的过程中生成了NO分子; N2+离子是N原子缔合电离的产物。 其中激波速度低于5 450 m· s-1时OH(A-X)的相对强度最大, NH(A-X)特征光谱在激波速度5 008 m· s-1的时候出现, 之后随着速度的增大NH(A-X)的相对强度逐渐增加, 在激波速度5 735 m· s-1的高温辐射光谱中特征光谱NH(A-X)谱峰的相对强度最大。 随着激波速度的增加相对强度最高的依然是NH(A-X)特征光谱; 特征光谱 N2+(B-X)在激波速度6 240 m· s-1出现, N2+(B-X)特征光谱的相对强度随速度增加, 直到激波速度7 686 m· s-1之后不再增加, N2+(B-X)相对强度随速度的变化情况与计算结果基本符合。 最后分析了弛豫时间随着激波速度的变化情况, 随着激波速度增加激波波后空气激发的弛豫时间逐渐缩短, 激波速度和弛豫时间的关系近似为指数关系。

参考文献
[1] Yan X, Huang H, Fan Z, et al. Polymer Composites, 2022, 43(11): 8341. [本文引用:1]
[2] LUO Jie, MA Hao-jun, WANG Guo-lin, et al(罗杰, 马昊军, 王国林, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(7): 2135. [本文引用:1]
[3] Liu J, Li K, Liu W. Chinese Journal of Aeronautics, 2015, 28(1): 57. [本文引用:1]
[4] Cruden B A, Brand is A M. Journal of Thermophysics and Heat Transfer, 2020, 34(1): 154. [本文引用:1]
[5] Brand is A M, Johnston C O, Cruden B A, et al. Journal of Thermophysics and Heat Transfer, 2017, 31(1): 178. [本文引用:2]
[6] Johnston C O. Journal of Thermophysics and Heat Transfer, 2021, 35(2): 349. [本文引用:1]
[7] Brand is A M, Johnston C O, Cruden B A, et al. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, 121: 91. [本文引用:1]
[8] Lemal A, Nishimura S, Nomura S, et al. 54th AIAA Aerospace Sciences Meeting, 2016. [本文引用:1]
[9] Takayanagi H, Fujita K. 44th AIAA Thermophysics Conference, 2013. [本文引用:1]
[10] Dikalyuk A S, Surzhikov S T. High Temperature, 2014, 52(1): 35. [本文引用:1]
[11] Kozlov P V, Zabelinsky I E, Bykova N G, et al. Acta Astronautica, 2022, 194: 461. [本文引用:1]
[12] Kozlov P V, Zabelinsky I E, Bykova N G, et al. Russian Journal of Physical Chemistry B, 2021, 15(6): 989. [本文引用:1]
[13] LÜ Jun-ming, LI Fei, LI Qi, et al(吕俊明, 李飞, 李齐, 等). Acta Aeronautica et Astronautica Sinica(航空学报), 2022, 43(3): 626551. [本文引用:1]
[14] LÜ Jun-ming, LI Fei, LIN Xin, et al(吕俊明, 李飞, 林鑫, 等). Journal of Experiments in Fluid Mechanics(实验流体力学), 2019, 33(3): 25. [本文引用:1]
[15] Dubuet U, Nomura S, Matsuyama S, et al. Journal of Thermophysics and Heat Transfer, 2020, 34(4): 725. [本文引用:1]
[16] Krähling T, Geisler S, Okruss M, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2015, 114: 20. [本文引用:1]
[17] Volynets V, Barsukov Y, Kim G, et al. Journal of Vacuum Science & Technology A, 2020, 38(2): 023007. [本文引用:1]
[18] Kadochnikov I N, Arsentiev I V. Journalof Physics D: Applied Physics, 2018, 51: 374001. [本文引用:2]
[19] Karpuzcu I T, Jouffray M P, Levin D A. Journal of Thermophysics and Heat Transfer, 2022, 36(4): 982. [本文引用:1]
[20] Wang C, Wu Y, Chen Z, et al. Plasma Scinece and Technology, 2016, 18(7): 732. [本文引用:1]
[21] Bodewits D, Országh J, Noonan J, et al. The Astrophysical Journal, 2019, 885(2): 167. [本文引用:1]