光学常数是反映液体光学性质的重要参数, 其在液体成分的定性和定量分析、 液体的热辐射特性研究等方面具有重要应用。 液体光学常数的测量方法主要包括: 衰减全反射法^{[1, 2]}、 透射法^{[3, 4]}、 椭偏法^[5]、 双厚度透射法^{[6, 7, 8, 9, 10, 11, 12, 13, 14, 15]}。 前两种方法需联立Kramers-Kronig关系式进行求解, 但求解过程繁琐。 椭偏法可以快速精确获得液体的折射率, 但对于弱吸收液体, 椭偏法很难给出消光系数的精确结果。 双厚度透射法原理简单, 不需要采用Kramers-Kronig关系式, 对于弱吸收液体, 通过改变液体的厚度, 可获得精度较高的光学常数。

双厚度透射法由Tuntomo等^[6]提出, 其通过测量液体两个不同厚度的透射光谱, 然后反演确定了庚烷和癸烷的光学常数, 但由于忽略了液体池窗口玻璃的影响, 导致计算结果有误差。 Otanicar等^[7]利用双厚度透射法, 采用Large等^[16]提出的多层介质透射率模型测量了四种液体的光学常数, 但Large的模型在介质间引入了真空隔层, 导致Otanicar的结果也存在误差。 Li^[8]等提出了一种三层介质结构(液体池)并考虑层间多次反射的透射率模型, 该模型更适合于液体光学常数的测量。 双厚度透射法测量液体在两个不同厚度下的透射率, 建立关于光学常数的非线性方程组, 但由于三层介质结构的透射率方程极复杂, 难以求得其解析解, 因此均采用反演法来求解, 反演法的问题主要表现在计算耗时和存在迭代误差以及折射率的反演结果存在二值问题^{[7, 9]}。

当前, 直接求解三层介质结构透射率方程的尝试还未见报道。 本文在这一方面做了一些探索, 若液体的两个厚度满足整数比, 则经过代数运算, 就可得到与消光系数有关的多项式方程, 以及与折射率有关的一元二次方程。 这两个方程均可求得数值解和解析解, 从而避免了反演算法的耗时和迭代误差。 对于折射率反演的二值问题, 则引入第二液体池并测量一个厚度的透射率数据来唯一确定。 作为新方法的应用示例, 以文献[17]中水的光学常数作为“ 理论值” , 用文献[18]中的玻璃数据设定两个液体池窗口的光学常数并给定其厚度。 在不考虑仪器测量误差的情况下, 将文献数据代入透射率方程计算的透射率作为“ 实验数据” , 然后用多项式求根的方法确定了水的光学常数, 并给出了计算结果与“ 理论值” 的相对误差。

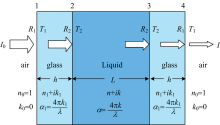
测量液体光学常数的液体池结构如图1所示, 构成液体池的两块窗口玻璃为同种材料, 厚度均为h。 玻璃的光学常数为已知量, 其折射率、 消光系数分别为n₁和k₁, 衰减系数α ₁=4π k₁/λ , 其中λ 为光在真空中的波长(下同)。 液体的厚度为L, 其折射率、 消光系数分别为n和k, 衰减系数α =4π k/λ 。 测量时将液体池置于空气中, 强度为I₀的平行光从液体池左侧垂直入射, 依次通过玻璃、 液体和玻璃, 最终从液体池右侧出射的光强为I。 由光线追迹法, 考虑光在三层结构的四个分界面(用1、 2、 3和4表示)上的多次反射和折射, 并忽略干涉效应时, 光通过液体池后的总透射率t_total=I/I₀可表示^{[8, 19]}为

$t_{\text {total }}=\frac{t_{34} t_{12} \exp (-\alpha L)}{1-r_{34} r_{21} \exp (-2 \alpha L)}$(1)

式(1)中, t₁₂为光通过左侧玻璃(考虑了光在分界面上的多次反射和折射, 脚标顺序表示光的传播方向, 下同)的透射率, t₃₄为光通过右侧玻璃的透射率; r₂₁为光从液体中入射到左侧玻璃时的反射率, r₃₄为光从液体中入射到右侧玻璃时的反射率。 由于液体池左右两侧玻璃的材料、 厚度均相同, 并考虑对称性, 有t₃₄=t₁₂, r₃₄=r₂₁, 而

$t_{12}=\frac{T_{1} T_{2} \exp \left(-\alpha_{1} h\right)}{1-R_{1} R_{2} \exp \left(-2 \alpha_{1} h\right)}$(2)

$r_{21}=R_{2}+\frac{T_{2}^{2} R_{1} \exp \left(-2 \alpha_{1} h\right)}{1-R_{1} R_{2} \exp \left(-2 \alpha_{1} h\right)}$(3)

式(2)和式(3)中, R₁、 T₁为分界面1和4上的界面反射率、 界面透射率; R₂、 T₂为分界面2和3上的界面反射率、 界面透射率。 将空气的折射率近似为1, 消光系数近似为0。 根据菲涅耳定律和斯涅耳定律有

$R_{1}=\frac{\left(n_{1}-n_{0}\right)^{2}+\left(k_{1}-k_{0}\right)^{2}}{\left(n_{1}+n_{0}\right)^{2}+\left(k_{1}+k_{0}\right)^{2}}=\frac{\left(n_{1}-1\right)^{2}+k_{1}^{2}}{\left(n_{1}+1\right)^{2}+k_{1}^{2}}$(4)

$R_{2}=\frac{\left(n-n_{1}\right)^{2}+\left(k-k_{1}\right)^{2}}{\left(n+n_{1}\right)^{2}+\left(k+k_{1}\right)^{2}}$(5)

T1=1-R1(6)

T2=1-R2(7)

令t₁₂=m(1-r₂₁), 则联合式(2)、 式(3)、 式(6)和式(7)可得

m=1-R1exp⁡exp-α1h1-R1exp⁡exp-2α1h(8)

由式(8)可知, m由液体池窗口玻璃的厚度和光学常数确定, 于是将式(1)改写为

ttotal=m2(1-r21)2exp(-αL)1-r212exp(-2αL)(9)

设光通过液体厚度为L和iL(i=2, 3, 4, …)的液体池后的透射率为t₁和t_i, 为简单计, 令a=t₁/m²、 b=t_i/m², y=exp(-α L), 则由式(9)得

a=(1-r21)2y1-r212y2(10)

b=(1-r21)2yi1-r212y2i(11)

给式(10)两侧同乘以y^i-1, 联立式(11)消去两式右侧的分子, 有

ayi-1-b=(ayi-1-by2(i-1))y2r212(12)

将式(12)中的r₂₁代入式(10), 经过代数运算可得关于y的4i次多项式方程

∑j=04ipjyj=0(13)

其中, 多项式方程的系数如表1所示, 表1仅列举了四种厚度组合, 分别为L和2L、 L和3L、 L和4L、 L和5L, 相应组合分别对应y的8、 12、 16、 20次多项式方程。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 测量液体光学常数的液体池结构Fig.1 Liquid cell structure for measuring liquid optical constants

表1

Table 1

表1(Table 1)

表1 不同厚度组合的多项式方程及其对应的多项式系数 Table 1 Polynomial equations and their corresponding polynomial coefficients of different thickness combinations L and 2L L and 3L L and 4L L and 5L ∑j=08pjyj=0 ∑j=012pjyj=0 ∑j=016pjyj=0 ∑j=020pjyj=0 p8=b2 p7=-2ab(1+b) p6=a2(1+b)2 p5=2ab(1+b) p4=-2(a2+a2b2+b2) p3=2ab(1-b) p2=a2(1-b)2 p1=-2ab(1-b) p0=b2 p12=b2 p11=-2ab2 p10=a2b2-2ab p9=2a2b p8=a2+2ab p7=2a2b+2ab2 p6=-2a2-2a2b2-2b2 p5=-2a2b-2ab2 p4=a2+2ab p3=-2a2b p2=a2b2-2ab p1=2ab2 p0=b2 p16=b2 p15=-2ab2 p14=a2b2 p13=-2ab p12=2a2b p11=2ab p10=a2+2a2b p9=2ab2 p8=-2a2-2a2b2-2b2 p7=-2ab2 p6=a2-2a2b p5=2ab p4=-2a2b p3=-2ab p2=a2b2 p1=2ab2 p0=b2 p20=b2 p19=-2ab2 p18=a2b2 p17=0 p16=-2ab p15=2a2b p14=2ab p13=2a2b p12=a2 p11=2ab2 p10=-2a2-2a2b2-2b2 p9=-2ab2 p8=a2 p7=-2a2b p6=2ab p5=-2a2b p4=-2ab p3=0 p2=a2b2 p1=2ab2 p0=b2

表1 不同厚度组合的多项式方程及其对应的多项式系数 Table 1 Polynomial equations and their corresponding polynomial coefficients of different thickness combinations

式(13)是关于y的一元多项式方程, 通过数值求解可得其根, 但只有满足0< y< 1的根才有实际物理意义。 则液体的衰减系数和消光系数分为

α=-ln(y)L(14)

k=-λln(y)4πL(15)

另由式(10)可得

r212(ay2+y)-2yr21+(y-a)=0(16)

式(16)是关于r₂₁的一元二次方程, 由于其判别式非负, 又因0< r₂₁< 1, 则方程(16)的解为

r21=1-a(a-y+1/y)ay+1(17)

则将式(17)和式(7)代入式(3)、 可得

R2=r21-R1exp(-2α1h)1+(r21-2)R1exp(-2α1h)(18)

则由式(18)和式(15)代入式(5)可得液体的折射率为

n=n1(1+R2)1-R2±4n12R2(1-R2)2+R2(k+k1)2-(k-k1)21-R2(19)

由于液体折射率与液体池窗口玻璃材料折射率的大小关系未知, 所以式(19)中的加减号不能确定, 则求解的液体折射率存在二值问题。 为此, 可另外选择一种窗口玻璃材料制作液体池, 其折射率、 消光系数分别为n₂和k₂, 衰减系数α ₂=4π k₂/λ , 要求在测量光谱范围内n₂≠ n₁。 再测量液体在此液体池中某一厚度(为简单计可取为L)时的光谱透射率, 然后结合已经确定的消光系数再作相关计算, 会另外得到液体的两个折射率值, 这样在四个折射率中, 数值相同者即为液体的折射率。

具体的实验测量和计算流程如下: 用光学常数为n₁和k₁的玻璃制作液体池1, 其两侧玻璃的厚度均为h, 用光学常数为n₂和k₂的玻璃制作液体池2, 其两侧玻璃的厚度也为h(注: 厚度也可与液体池1的不同)。 第一步: 用液体池1测量液体厚度分别为L、 iL的透射率t₁和t_i, 由式(4)计算R₁, 连同h和α ₁一起代入式(8)计算得到m, 然后计算a=t₁/m²、 b=t_i/m²; 接下来由式(13)求多项式方程的根y, 由式(14)、 式(15)计算液体的衰减系数、 消光系数, 再由式(17)、 式(18)和式(19)依次计算得到两个折射率值。 第二步: 用液体池2测量液体厚度为L时的透射率t₁, 用液体池2的光学常数代入式(4)重新计算R₁, 连同h和α ₂一起代入式(8)计算用液体池2时的m, 然后计算a=t₁/m²。 将a和第一步所求多项式方程的根y代入式(17)重新计算r₂₁, 再用式(18)重新计算R₂, 最后用n₂和k₂代替式(19)中n₁和k₁计算折射率的另外两个值。 第三步: 从四个折射率值中, 选择相同的值作为液体的折射率, 从而完成液体光学常数的确定。

上述计算避免了反演迭代过程, 所以结果中不存在反演误差。 只要液体的两个厚度满足整数比关系, 均可按照上述方法进行计算(注: 表1中未列出的其他厚度组合, 需要重新推导其多项式系数), 其中整数比越小(小厚度∶ 大厚度), 则液体两个厚度的差别越大, 光谱透射曲线的区别也越明显, 这有利于提高实验仪器测量的精确度。 如果两个厚度不是最简整数比(比如2L和4L组合的整数比为2∶ 4, L为基准厚度), 则可将其化简(如1∶ 2), 然后用相应的最简整数比所对应(如8次)多项式方程求解即可, 但相应的基准厚度为整数比的最大公约数乘以L(如2L), 在用式(14)、 式(15)计算时要用2L代替公式中的L。

由式(15)和式(19)可知, 液体的消光系数可以唯一确定, 但其折射率存在二值问题。 由式(5)可知, 当消光系数确定后, 由于式中存在折射率的平方项, 导致满足式(5)的折射率有两个值, 这也是前述反演法中折射率存在二值问题的原因所在。

反演法确定液体光学常数的一般做法为^[6]: 在开始迭代之前, 先给定待测液体光学常数的初值, 然后不断调整其取值, 直到将其代入式(1)或式(9)计算所得的透射率收敛于实验所测透射率数据, 于是终止迭代并得到光学常数。 反演法的问题首先是计算耗时; 其次是初始值的设置不当会增加迭代时间, 也会导致收敛到错误的结果从而出现折射率的二值问题; 最后还可能出现迭代不收敛导致结果有较大误差的现象。 因此, 研究者在反演法中结合其他方法如椭偏法^{[10, 11, 12]}来给定恰当初值, 以加快迭代进程并促使反演收敛到正确的结果, 来消除折射率的二值问题; 在反演法中引入遗传算法^{[9, 13]}、 共轭梯度法^{[11, 12]}、 粒子群优化算法^{[14, 15]}以加快计算效率来减少计算耗时。 上述努力为反演法带来了改进但没有从根本上解决反演法的问题。

多项式求根法通过设定液体的两个厚度满足整数比关系, 将复杂三层介质结构的透射率方程的求解转化为多项式求根问题, 而多项式求根问题是可以快速实现并能求得其高精度的数值解; 对折射率的二值问题, 通过引入第二液体池即可解决。 比较而言, 反演法是同时确定液体光学常数的两个参量, 而多项式求根法是分步确定, 即先用多项式求根法确定消光系数, 而后求解一元二次方程确定折射率。 多项式求根法简化了复杂方程的求解, 解决了反演法的上述问题, 实现了光学常数的精确确定。

选用文献[17]中水在0.5~1.0 μ m光谱范围的光学常数作为“ 理论值” , 液体池1和液体池2的窗口材料分别选用文献[18]中的石英玻璃和有机玻璃, 相应的光学常数如表2所示。

表2

Table 2

表2(Table 2)

表2 水和液体池在0.5~1.0 μ m的光学常数 Table 2 Optical constants of water and liquid cell in the spectral range of 0.5~1.0 μ m wavelength /μ m water[17] liquid cell 1[18] liquid cell 2[18] n k n1 k1 n2 k2 0.5 1.335 1.00× 10-9 1.515 0.8× 10-7 1.509 3.1× 10-7 0.6 1.332 1.09× 10-8 1.509 0.8× 10-7 1.496 3.2× 10-7 0.7 1.331 3.35× 10-8 1.517 1.1× 10-7 1.501 3.2× 10-7 0.8 1.329 1.25× 10-7 1.554 1.3× 10-7 1.536 2.8× 10-7 1.0 1.327 2.89× 10-6 1.548 0.9× 10-7 1.521 1.2× 10-7

表2 水和液体池在0.5~1.0 μ m的光学常数 Table 2 Optical constants of water and liquid cell in the spectral range of 0.5~1.0 μ m

两个液体池玻璃的厚度均为1 mm, 液体池1中待测液体的厚度可调, 分别设定为10和20 mm, 液体池2中待测液体的厚度设定为10 mm。 将表2中的光学常数代入式(1), 计算得到的透射率作为“ 实验数据” , 结果如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 水的透射率数据Fig.2 Water transmittance data

如图2所示, 在0.5~1.0 μ m的光谱范围内, 用液体池1和水的光学常数计算了水的厚度分别为10和20 mm的透射率数据, 以及用液体池2和水的光学常数计算了水的厚度为10 mm时的透射率数据。 由于液体池1所测水的两个厚度满足整数比1∶ 2, 即厚度组合为L和2L的情况, 对应的液体基准厚度L=10 mm。 该厚度组合对应的多项式方程为8次, 相应的多项式方程的系数为表1中第1列的数据。 基于多项式求根法, 首先用液体池1所计算的两个透射率数据可以唯一地确定水的消光系数, 而水的折射率会有两个值; 接下来则用已经确定的消光系数和液体池2所计算的透射率数据再得到水的折射率的两个值, 选择相同的值作为水的折射率, 从而实现水的光学常数的确定, 结果如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
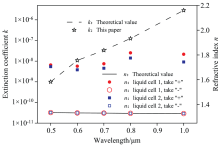	图3 基于多项式求根法确定水的光学常数Fig.3 Determination of optical constants of water based on polynomial root finding

如图3所示为0.5~1.0 μ m的光谱范围内, 用多项式求根法所确定的水的光学常数。 从图中水的消光系数可以看出, 本文方法的计算结果与表2中水的消光系数的理论值符合的很好, 其最大相对误差为1.51× 10^-8%。 而折射率的计算结果有四组值, 其中相同的两组值正是水的折射率, 其结果与表2中水的折射率的理论值符合的也很好, 其最大相对误差为9.83× 10^-11%。 模拟结果表明, 多项式求根法解决了反演法的计算耗时和迭代误差问题, 引入第二液体池也解决了折射率的二值问题, 用本文方法可以实现液体光学常数的确定。

上述模拟计算是在不考虑实验仪器测量误差的情况下, 用构造的“ 实验数据” 来展示多项式求根法的具体应用, 结果显示多项式求根法能从“ 实验数据” 精确解算出液体的光学常数, 模拟计算初步表明该方法是可行的。 实际上, 多项式求根法并未对实验测量条件(如光度计、 光谱仪的精度等)提出更苛刻的要求。 在基于双厚度透射法确定液体光学常数的实验中, 当液体的两个厚度满足整数比时, 则可用多项式求根法替代反演法来完成相关计算, 其中消光系数可直接计算得到, 但折射率的确定还需补充第二液体池的实验测量数据。

由于上述模拟计算所用的数据并非实验测量数据, 所以计算结果的相对误差极小。 但在实际测量中有各种影响因素, 比如光谱仪探测器的非线性会影响透射率数据的测量精度; 液体厚度测量不准确则会导致液体厚度组合不严格满足整数比; 液体池窗口玻璃的光学常数的精度及窗口玻璃厚度制备的精度等因素都会导致计算所得的光学常数出现误差, 这些因素的影响有待进一步的实验测量来研究。 另外需要指出的是, 液体的两个厚度组合应根据其在测量光波段的吸收大小来合理选择, 要使实验仪器能够在其灵敏度范围内测量出高精度的透射率数据。 对于液体吸收较小的光波段, 应当选择厚度的整数比较小的组合, 也即液体的两个厚度差别较大, 从而使两个厚度的透射曲线有明显的区别, 来提高实验测量的精度; 反之应选择厚度的整数比较大的组合。 例如: 由表2知水在波长为0.5 μ m处消光系数很小, 在该处用液体池1计算水厚度分别为10和20 mm的透射率的差值为0.000 23, 这一差值在模拟计算时可以得到正确的结果, 但实际测量时要考虑仪器的灵敏度是否能分辨这一微小差值。

以三层介质结构(液体池)的双厚度透射率模型为基础, 通过将液体的两个厚度设定为整数比, 实现了将复杂的光谱透射率方程转化为与消光系数有关的多项式方程, 以及与折射率有关的一元二次方程。 通过多项式方程求根的方法实现了液体光学常数的确定, 从而避免了反演法的耗时和迭代误差; 引入第二液体池则解决了折射率的二值问题。 最后用已知文献的数据进行模拟计算来展示本文所提方法的使用流程。 结果表明新的方法是可行的。 本文的工作为双厚度透射法确定液体光学常数提供了一个新选择。

当然, 本文的模拟计算是理想情况, 没有考虑实际测量当中影响透射率数据的其他因素, 如液体厚度组合不满足整数比, 液体池窗口玻璃光学常数的精度等。 考虑这些因素, 进行实验测量并对本文方法加以验证是后续的工作。 另一方面, 本文所提的多项式求根法仍稍显复杂繁琐, 进一步研究找到光谱透射率方程的解析解也是值得探索的方向。