引用本文
吴护林, 邓贤明, 张天才, 李忠盛, 岑奕, 汪家辉, 熊杰, 陈知华, 林牧春. 一种基于目标与背景特征分离模型的高光谱目标检测修正算法[J]. 光谱学与光谱分析, 2024,44(1): 283-.
WU Hu-lin, DENG Xian-ming, ZHANG Tian-cai, LI Zhong-sheng, CEN Yi, WANG Jia-hui, XIONG Jie, CHEN Zhi-hua, LIN Mu-chun. A Revised Target Detection Algorithm Based on Feature Separation Model of Target and Background for Hyperspectral Imagery[J]. Spectroscopy and Spectral Analysis, 2024,44(1): 283-.
Doi:10.3964/j.issn.1000-0593(2024)01-0283-09  
Permissions
Copyright©2024, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
一种基于目标与背景特征分离模型的高光谱目标检测修正算法
吴护林1, 邓贤明1,*, 张天才1, 李忠盛1, 岑奕2, 汪家辉1, 熊杰1, 陈知华1, 林牧春1
1.中国兵器工业第五九研究所, 重庆 401329
2.中国科学院空天信息创新研究院, 北京 100101
*通讯作者 e-mail: 15198121267@163.com

作者简介: 吴护林, 1964年生, 中国兵器工业第五九研究所研究员, 中国南方工业集团有限公司首席科技专家 e-mail: zscqforwj_mail@163.com

收稿日期: 2022-08-27 接受日期: 2022-11-15
基金: 科工局课题(HDH59030303), 装发领域基金项目(61402080404)资助
摘要

高光谱图像立方体数据可以提供成像场景中地物在可见光和近红外波长范围内的空间信息和地物属性诊断的光谱特征信息, 在目标检测与识别方面拥有得天独厚的天然优势。 然而, 基于高光谱图像数据的目标检测也存在一定缺陷, 如经典的高光谱目标检测算法仅利用光谱维度信息检测目标, 检测模型要么对背景高维特征矩阵构建的准确度不足, 要么对背景先验光谱特征的完备性要求较高, 导致算法对不同复杂度的检测场景适应性不强。 因此, 基于计算复杂度较低、 参数需求量较少且检测性能较为优异的经典多目标检测算法—多目标约束能量最小化(MCEM), 提出了一种基于目标与背景环境特征分离模型的高光谱目标检测修正算法(R-MCEM)。 首先, 设计了一个与目标形状、 尺寸相近的逐像元移动运算窗口, 依次计算窗口中的每个像元与窗口内其他像元的光谱距离之和D1, 像元与各类目标的光谱距离之和D2。 其次, 采用获得D1/D2最小值的像元替换窗口内的所有像元值。 然后, 自左向右、 自上而下逐像元移动窗口, 重复窗口内每一个像元与目标、 背景像元的光谱距离运算, 并确定窗口内与背景相似度最高、 与目标相似度最低的像元。 直到移动运算窗口遍历整个高光谱图像, 大幅提升了基于目标与背景环境特征分离的背景高维特征矩阵准确度。 分别设计了基于实测高光谱图像数据和模拟图像数据的修正检测算法性能验证试验, 并采用三维操作特征曲线(3D ROC)结合目标与背景分离度(SDBT)开展修正算法的检测精度评估。 试验结果表明, 提出的修正算法有效减少了虚警率, 提高了检测精度。 基于实测数据的检测精度、 目标与背景分离度由MCEM算法的0.937 7、 0.57提升到R-MCEM的0.993 5、 0.67, 基于模拟数据的亚像元检测能力由MCEM的20%丰度提升到R-MCEM的15%丰度。

关键词: 高光谱目标检测; 目标与背景特征分离模型; 3D ROC; SDBT
中图分类号:TP79 文献标志码:A
A Revised Target Detection Algorithm Based on Feature Separation Model of Target and Background for Hyperspectral Imagery
WU Hu-lin1, DENG Xian-ming1,*, ZHANG Tian-cai1, LI Zhong-sheng1, CEN Yi2, WANG Jia-hui1, XIONG Jie1, CHEN Zhi-hua1, LIN Mu-chun1
1. The 59th Research Institute of China Ordnance Industry, Chongqing 401329, China
2. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China
*Corresponding author
Abstract

Hyperspectral imagery cube Data can provide spatial information and diagnostic spectral characteristics, in the range of visible and near-infrared wavelength, about the attributes of materials in the scene, which contribute to the unique advantage of hyperspectral imagery for target detection. However, hyperspectral target detection has some shortcomings, such as the classical hyperspectral target detection algorithm only uses the information of spectral dimension to detect the target. The detection model either has insufficient accuracy for the construction of background high-dimensional f characteristics matrix or has high requirements for the completeness of background prior spectral characteristics, resulting in poor adaptability of the algorithm to different scenarios. Therefore, based on the classic multi-target detection algorithm-multiple target constrained energy minimization (MCEM), which has low computational complexity, fewer parameter requirements and better detection performance, this paper proposes a modified algorithm R-MCEM (revised MCEM) based on the separation model of target and background. First of all, this algorithm designs a pixel-by-pixel moving operation window that is similar to the shape and size of the target and sequentially calculates the spectral distances between each pixel and other pixels in the window, referred to as D1, and the spectral distances between the pixel and all targets,referred as D2. Next, all pixel values in the window are replaced with the pixel obtaining the minimum value of D1/D2. Then, move the window from left to right and from top to bottom and repeat the same calculation. Until the moving operation window traverses the entire hyperspectral image, all the interested targets in the hyperspectral image are eliminated as much as possible, and the accuracy of the background high-dimensional characteristics matrix is greatly improved. In this paper, the performance verification tests of the modified detection algorithm based on the true hyperspectral image data and the simulated image data are designed respectively, and the detection accuracy evaluation of the proposed algorithm is carried out by the three-dimensional receiver operation characteristics curve (3D ROC) combined with the Separation Degree Between Background and Target(SDBT). The experimental results show that the proposed algorithm can effectively reduce the false alarm rate and improve the detection accuracy. The detection accuracy and SDBT based on the actual data are increased from 0.937 7 and 0.61 of the MCEM algorithm to 0.993 5 and 0.71 of R-MCEM, and the sub-pixel detection ability based on the simulated data is increased from 20% abundance of MCEM to 15% abundance of R-MCEM.

Keyword: Hyperspectral target detection; Separation model between target and background; 3D ROC; SDBT
引言

高光谱目标检测算法充分利用高光谱图像丰富的反射光谱信息, 通过构建物体光谱特征与其空间信息的匹配分析模型[1, 2, 3]实现复杂背景中目标的空间定位与属性识别。 该领域的经典算法主要包括约束能量最小化(CEM)算法[4], 自适应一致估计(ACE)算法, 自适应匹配滤波器(AMF)算法[5], 正交子空间投影(OSP)算法[6]和异常检测算法RXD(Reed-Yu检测器)、 UTD(统一目标检测器)、 LPTD(低概率目标检测器)[7, 8, 9]。 OSP算法的准确度受目标及其背景先验信息的完整度影响较大, 且OSP算法抑制噪声和消除未知信号的性能很差[10, 11]。 异常检测算法将光谱特征不符合全局或局部背景光谱信号模型的像素认定为异常, 但这些异常不一定是感兴趣的目标[12, 13]。 此外, 这些异常很有可能包含一些干扰信息[13, 14, 15], 如能量低或丰度小的噪声和非目标。 Harsanyi提出了CEM算法, Kraut和Scharf提出了ACE算法, Fuhrmann提出了AMF算法, 与异常检测算法相比, 这些算法的目标导向性更强, 噪声抑制和未知信号消除能力远强于OSP算法。 但ACE和AMF适用于符合正态分布的高光谱数据, 而高光谱数据通常满足流形分布模型[16]。 CEM算法的性能与高光谱数据的分布模型无关, 实用性更高。 但CEM不能对具有相似特征的同类型目标进行分类, 对目标先验光谱的准确度敏感性较高。 为了解决这个问题, Chang和Du等提出了多目标约束能量最小化(multiple-target constrained energy minimization, MCEM)、 Sum CEM(SCEM)和Winner-Take-All CEM(WTACEM)[17]。 不仅解决了CEM对目标光谱的敏感性和噪声辨别能力的不足, 还突破了单目标检测的限制。 因此, 这些改进算法综合了多属性目标检测、 噪声抑制和对频谱不敏感的优点。 但是, 与CEM类似, 这些方法也存在背景高维特征矩阵构建准确度不足的缺陷。 考虑到CEM与MCEM数学原理相同, 公式形式也相似, 提出了一种基于目标与背景特征分离模型的修正MCEM算法。 由于传统2D ROC对于两个性能相近的检测器性能评估能力较弱, 采用三维操作特征曲线(three dimensional receiver operation characteristics curve, 3D ROC)[18, 19]及其生成的背景分离度(separation degree between background and target, SDBT)(背景和目标分离度)全面评估检测精度。

1 算法原理
1.1 目标与背景特征分离模型

经典算法 MCEM 的数学表达式见式(1)

DMCEM(xi)=xTiR-1DDTR-1D×1(1)

式(1)中, R=1N∑i=1NxixTi为背景自相关矩阵, D={d1, d2, d3, …, dq}为由q个光谱特征组成的目标特征矩阵, T表示矩阵转置运算, 1是值均为1的q× 1约束向量。 在没有背景先验信息的情况下, MCEM算法采用整幅图像的信息构建背景特征矩阵, 即R包括了目标信息的自相关矩阵, 导致MCEM算法对于不同应用场景的目标检测适用性不强。 为了消除R中的目标自相关矩阵, 提升高光谱图像的背景高维特征矩阵准确度与目标检测识别精度, 提出了目标与背景特征分离模型。

首先, 设计一个大于目标尺寸的移动操作窗口, 依次计算每个像元与窗口中其他像元的光谱距离D1, 以及该像元与目标之间的光谱距离D2, 如果没有目标的先验光谱信息则D2恒为常数1, D1、 D2的计算方法见式(2)和式(3)

D1=∑OPD[f(xi), f(xj)]|xi, xj∈W(2)

D2=∑OPD[f(xi), d(xj)]|xi∈W, j∈D(3)

式中, W、 D分别为移动运算窗口和目标特征矩阵的值域。 OPD(orthogonal projection divergence)为高维向量间距离的度量方法[20], 其数学表达式见式(4)和式(5)

OPD(xi, xj)=(xTiPxj⊥xi+xTjPxi⊥xj)12(4)

PxN⊥=IL×L-xN(xTNxN)-1xTN(5)

其中, N=i、 j, IL× L为L× L维单位矩阵。

然后, 在D1和D2的双重约束下, 将取得 D1/D2最小值的像元P1定义为与目标特征相似度最低而与背景特征相似度最大的像元, 并以P1替换运算窗口中的所有像元。 最后, 逐像元移动运算窗口并重复上述计算过程, 直到窗口遍历整个图像即完成目标与背景特征分离模型构建。 此时, 高光谱图像的背景特征矩阵可由式(6)或式(7)表示

R* =R-1N∑i=1m(aid)2didTi(6)

C* =C-1N∑i=1m(aid)2(di-ui)(di-ui)T(7)

式中, R* 、 R分别为背景和整幅图像的自相关矩阵, C* 、 C分别为背景和整幅图像的协方差矩阵。 m为目标个数, aid为目标占据像素的丰度, di为目标向量, ui波段均值。

基于上述目标与背景分离模型的构建, 高光谱目标检测修正算法(revised MCEM, R-MCEM)的构建流程见图1。

图1 高光谱目标检测修正算法构建流程Fig.1 Construction process of modified hyperspectral target detection algorithm

1.2 目标与背景分离度评估方法

基于目标检测精度评估方法3D ROC, 构建目标与背景分离度参数模型SDBT, 见式(8)

SDBT=pd(2)Δτ2+∑i=2n[pd(i)+pd(i+1)]Δτ2-pf(2)Δτ2+∑i=2n[pf(i)+pf(i+1)]Δτ2pd(2)Δτ2+∑i=2n[pd(i)+pd(i+1)]Δτ2(8)

式(8)中, pd为不同阈值条件下的目标检测率向量, pf为不同阈值条件下的虚警率向量, τ 表示阈值向量, 其值域范围为0到1、 向量元素数量一般不少于2 000, Δ τ 为阈值增长的步长, pd(2)Δτ2+∑i=2n[pd(i)+pd(i+1)]Δτ2表示检测率和阈值关系函数与坐标横轴(阈值)围成面积, pf(2)Δτ2+∑i=2n[pf(i)+pf(i+1)]Δτ2表示虚警率和阈值关系函数与坐标横轴(阈值)围成面积, SDBT值域范围为0到1, 通常SDBT大于0.5的检测器性能较优。

2 实验部分
2.1 实测高光谱数据

通过成像光谱仪实测了由草地、 土壤等地物组成背景, 目标包括浅绿色、 深绿色和暗绿色3种织物的高光谱图像, 如图2(a)所示。 该数据由300× 400像素组成, 其中目标包含50个像素, 目标和背景的光谱反射率曲线如图2(c)所示。

图2 实测高光谱数据
(a): 实测高光谱图像; (b): 目标分布; (c): 实测图像光谱Fig.2 true experimental data
(a): True hyperspectral image; (b): Distribution of targets; (c): Spectra of true data

2.2 模拟高光谱数据

为了定量验证本算法的目标检测性能, 将ENVI软件光谱库的三种植物光谱(blue sprush needle、 dry long grass和black brush leaves)按照不同丰度植入真实高光谱图像。 真实高光谱数据是由数字图像和遥感实验室与Spec TIR有限公司收集的美国罗彻斯特航空高光谱数据[21], 模拟高光谱数据如3(a)所示。 该数据包括413.9~2 452.8 nm范围内的360个波段, 光谱分辨率和空间分辨率分别为5 nm和1 m, 数据大小为367× 319像素, 目标像素为5× 5。 模拟高光谱数据的光谱反射率曲线见图3(c)。

图3 模拟实验数据
(a): 模拟高光谱图像; (b): 目标分布; (c): 模拟图像光谱Fig.3 Simulated experimental data
(a): Simulated image; (b): Distribution of targets; (c): Spectra of simulated data

3 结果与讨论
3.1 基于实测高光谱数据的检测

采用MCEM和R-MCEM算法开展基于真实高光谱数据的目标检测实验, 检测结果如图4所示。 由于目标与背景中草地的光谱相似性较高, MCEM算法的检测结果中, 目标周围存在较多虚警信息, 甚至一些背景区域的检测统计量大于目标区域的检测统计量, 如图5(a)所示。 相比之下, R-MCEM则极大抑制了背景干扰, 见图5(b)。

图4 真实实验数据的目标检测结果
(a): MCEM检测结果; (b): R-MCEM检测结果Fig.4 Detection results of true data
(a): MCEM detection result; (b): R-MCEM detection result

图5 真实试验数据的目标检测3D统计量
(a): MCEM检测统计量; (b): R-MCEM检测统计量Fig.5 3D detection statistics for true data detection result
(a): Detection statistics of MCEM; (b): Detection statistics of R-MCEM

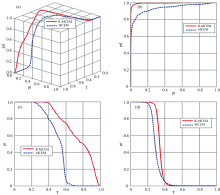
真实实验数据的检测评价结果见图6、 表1。 结果表明, 相比于MCEM算法, R-MCEM 算法的检测精度更高、 对于目标和背景的分离度更好。

图6 真实实验数据的3DROC评价结果Fig.6 3D ROC of detection result for true data

表1 真实实验数据的检测精度 Table 1 Accuracy of detection results for true data
3.2 基于模拟高光谱数据的检测

采用MCEM和R-MCEM算法开展基于模拟高光谱数据的目标检测实验, 检测结果见图7, 精度评价结果图8、 图9。 结果表明, MCEM和R-MCEM算法都具有较高的检测精度, 但与MCEM算法相比, R-MCEM算法可以进一步抑制背景值, 虚警率更低。 如图10表明两种算法对三个目标的检测率均为100%, 但R-MCEM算法检测的背景值主要分布在0.15左右, 而MCEM算法检测的背景值主要分布在0.23左右。

图7 模拟试验数据的检测结果
(a): MCEM检测结果; (b): R-MCEM检测结果Fig.7 Detection result of simulated data
(a): MCEM result; (b): R-MCEM result

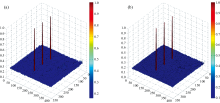图8 模拟实验数据的目标检测3D统计量
(a): MCEM检测统计量; (b): R-MCEM检测统计量Fig.8 3D detection statistics for simulated data detection result
(a): Detection statistics of MCEM; (b): Detection statistics of R-MCEM

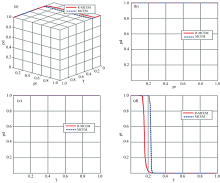图9 R-MCEM与MCEM算法检测结果的3DROC分析
注: 在(b)和(c)中, 数据点都落在坐标轴上, 如表2所示Fig.9 3D ROC curves analysis of the detection result of R-MCEM algorithm and MCEM algorithm
注: In Fig.9 (b) and (c), the data points distribute across the axis, as shown in the table 2

图10 模拟图像不同丰度目标的检测结果Fig.10 Detection results for simulated data with different targets fractions

为了进一步探索R-MCEM算法的亚像元检测性能, 我们将80%、 60%、 40%、 25%、 15%和10%等6种不同丰度的目标光谱植入真实图像中。 MCEM和R-MCEM算法的检测结果如图10所示。

图10的检测结果表明, 相比MCEM算法15%丰度的亚像元目标检测能力, R-MCEM算法能检测到丰度为10%的亚像元目标。 但不可忽视的是, 目标的形状很大程度上有助于目标的识别。 如果目标分散在整个图像中, 而不是集中在一块, 当目标的丰度很低时, 我们无法检测到目标。 事实上, 本文提出的修正算法并不能提高亚像元目标的检测精度, 原因在于本设计的运算窗口的尺寸必须大于单个像元, 否则执行R-MCEM算法时窗口内不会发生任何运算。 但是当处于亚像元状态的目标像聚集在一块时, R-MCEM算法则能发挥作用。 如图11、 表2所示, 当目标丰度不小于40%时, 两种算法的检测效果都很好, SDBT的值均大于0.452, 传统的目标检测精度评价结果2D AUC 均为1。 当目标丰度不大于25%时虚警急剧上升, 当目标丰度降至15%时MCEM算法几乎不能检测到目标, 而R-MCEM算法仍能将目标与背景分离。 但当目标丰度为10%时, R-MCEM算法的检测优势极小。 因此, MCEM和R-MCEM算法的亚像元检测能力, 分别为20%和15%的目标丰度。

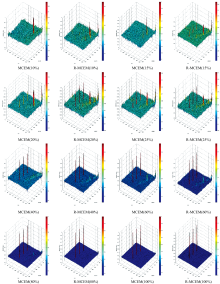图11 模拟图像不同丰度目标的3D检测统计量Fig.11 3D detection statistics for simulated data with different targets fractions

表2 不同丰度目标的检测精度 Table 2 Accuracy of detection results for targets with different fractions
4 结论

提出了一种基于目标与背景特征分离模型的高光谱目标检测修正算法R-MCEM以及目标与背景分离度评估方法SDBT, 并开展了基于实测及模拟数据的目标检测验证实验, 得到以下结论。

(1)通过构建目标与背景特征分离模型, 极大修正了原始目标检测算法MCEM的背景特征矩阵精度, 实现了目标与背景特征的分离度最大化, 通过构建目标与背景分离度评估方法, 实现了目标与背景分离度定量计算;

(2)验证实验结果表明, 基于实测数据的检测精度、 目标与背景分离度由原始算法MCEM的0.937 7、 0.57提升到修正算法R-MCEM的0.993 5、 0.67, 基于模拟数据的亚像元检测能力由原始算法MCEM的20%丰度提升到修正算法R-MCEM的15%丰度。

参考文献
[1] ZHANG Bing, GAO Lian-ru(张兵, 高连如). Hyperspectral Image Classification and Target Detection(高光谱图像分类与目标探测). Beijing: Science Press(北京: 科学出版社), 2011. [本文引用:1]
[2] TONG Qing-xi, ZHANG Bing, ZHANG Li-fu(童庆禧, 张兵, 张立福). National Remote Sensing Bulletin(遥感学报), 2016, 20(5): 689. [本文引用:1]
[3] Xie W, Zhang X, Li Y, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 5887. [本文引用:1]
[4] Harsanyi Joseph C (Won Nobel for Game Theory). Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences. Baltimore: Department of Electrical Engineering, University of Maryland Baltimore County, 1993. [本文引用:1]
[5] Kraut S, Scharf L L. IEEE Transactions on Signal Processing, 1999, 47(9): 2538. [本文引用:1]
[6] Harsanyi J C, Chang C I. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 779. [本文引用:1]
[7] PENG Bo, ZHANG Li-fu, ZHANG Peng, et al(彭波, 张立福, 张鹏, 等). National Remote Sensing Bulletin(遥感学报), 2017, 21(5): 739. [本文引用:1]
[8] Reed I S, Yu X. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(10): 1760. [本文引用:1]
[9] Yu X, Reed I S. IEEE Transactions on Signal Processing, 1993, 41(8): 2639. [本文引用:1]
[10] Qian D, Ren H. Proc SPIE, 2002, 4725: 501(doi: DOI:10.1117/12.478783). [本文引用:1]
[11] Chang C I. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1(doi: DOI:10.1109/TGRS.2021.3086768). [本文引用:1]
[12] Chang C I, Chiang S S. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(6): 1314. [本文引用:1]
[13] Hsueh M, Chang C I. IGARSS 2004. 2004 Geoscience and Remote Sensing Symposium, 2004, 5: 3222. [本文引用:2]
[14] Kwon H, Nasrabadi N M. IEEE Transactions on Geoscience & Remote Sensing, 2005, 43(2): 388. [本文引用:1]
[15] Lo E, Ingram J. Proc of SPIE, 2008, 6966: 696603. [本文引用:1]
[16] Zhai Y, Zhang L, Wang N, et al. IEEE Geoscience Remote Sensing Letter, 2016, 13(8): 1059. [本文引用:1]
[17] Ren H, Qian D, Chang C I, et al. Comparison Between Constrained Energy Minimization Based Approaches for Hyperspectral Imagery. IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data. IEEE, 2004. [本文引用:1]
[18] DENG Xian-ming, MIAO Fang, ZHAI Yong-guang, et al(邓贤明, 苗放, 翟涌光, 等). Acta Scientiarum Naturalium Universitatis SunYatseni[中山大学学报(自然科学版)], 2017, 56(1): 151. [本文引用:1]
[19] Chang C I. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(6): 5131. [本文引用:1]
[20] ZHAO Chun-hui, LI Xiao-hui, WANG Yu-lei(赵春晖, 李晓慧, 王玉磊). Journal of Electronic Measurement and Instrumentation(电子测量与仪器学报), 2014, 8: 803. [本文引用:1]
[21] Herweg J A, Kerekes J P, Weatherbee O, et al. SpecTIR Hyperspectral Airborne Rochester Experimental Data Collection Campaign. Proc. SPIE, 2012, 8390. [本文引用:1]