引用本文
梁龙, 吴珽, 沈葵忠, 熊智新, 许凤, 房桂干. 基于近红外光谱和水分校正算法的造纸木片基本密度预测[J]. 光谱学与光谱分析, 2023,43(8): 2476-2482.
LIANG Long, WU Ting, SHEN Kui-zhong, XIONG Zhi-xin, XU Feng, FANG Gui-gan. Prediction of Basic Density of Wood Chips Using Near-Infrared Spectroscopy and Moisture Content Correction Algorithm[J]. Spectroscopy and Spectral Analysis, 2023,43(8): 2476-2482.
Doi:10.3964/j.issn.1000-0593(2023)08-2476-07  
Permissions
Copyright©2023, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于近红外光谱和水分校正算法的造纸木片基本密度预测
梁龙1,2,3,4, 吴珽1,4,*, 沈葵忠1, 熊智新5, 许凤2,*, 房桂干1,*
1.中国林业科学研究院林产化学工业研究所; 江苏省生物质能源与材料重点实验室; 江苏省林业资源高效加工利用协同创新中心; 国家林业和草原局林产化学工程重点实验室; 林木生物质低碳高效利用国家工程研究中心, 江苏 南京 210042
2.北京林业大学材料科学与技术学院, 林木生物质化学北京市重点实验室, 北京 100083
3.中国林业科学研究院生态保护与修复研究所, 北京 100091
4.广西民族大学林产化学与工程国家民委重点实验室, 广西林产化学与工程重点实验室, 广西 南宁 530006
5.南京林业大学轻工与食品学院, 江苏 南京 210037
*通讯作者 e-mail: fangguigan@icifp.cn; xfx315@bjfu.edu.cn; wuting@icifp.cn

作者简介: 梁 龙, 1989年生, 中国林业科学院林产化学工业研究所助理研究员 e-mail: lianglong@icifp.cn

收稿日期: 2022-04-26 修回日期: 2022-08-16 接受日期: 2022-08-16
基金: 国家自然科学基金重大项目(31890771), 中国林业科学院林业新技术所基本科研业务费专项资金项目(CAFYBB2019SY039), 林产化学与工程国家民委重点实验室暨广西林产化学与工程重点实验室开放课题重点项目(GXFK2205)资助
摘要

基本密度是评估木材制浆造纸性能的重要指标。 采用近红外光谱技术检测造纸木片基本密度, 实时掌握原料材性变化, 能够为制定和优化制浆生产工艺提供基础理论数据。 但在实际生产中, 原料来源的复杂性造成木片水分含量波动较大, 光谱中的水分干扰信息严重影响模型预测效果, 成为制约近红外技术实际应用的主要因素。 以杨木片为研究对象, 通过对木片失水过程的近红外光谱动态监测, 结合主成分分析明确光谱中水分吸收信息的特征响应, 揭示了木片水分中结合水和自由水的变化规律。 分别采用不同水分条件下的木片光谱建立偏最小二乘回归(PLS)模型预测木片基本密度, 通过对比分析模型预测性能, 探究木片水分变化对近红外预测木片密度的影响, 并采用外部参数正交化算法(EPO)消除光谱中水分的干扰, 提高模型对水分变化的抗干扰能力。 研究结果表明, 基于饱水木片光谱的模型具有最好的预测精度, 模型的建立主要依靠近红外光谱对木片纤维结构特征信息的获取。 而光谱中大量的水分吸收信息对建模是冗余无用的, 并且会导致模型对样品水分高度敏感, 当测试集水分含量变化时, 模型预测出现严重偏差。 通过EPO算法对木片失水过程动态光谱的解析, 提取水分校正因子, 能够有效消除水分变化引起的光谱差异。 基于水分校正的基本密度预测模型对不同水分条件下的测试集均表现出稳定的预测性能, 均方根误差、 决定系数和预测相对标准偏差分别为12.23 kg·m-3、 0.883 4和2.93。 该研究将EPO算法引入对木材材性的近红外光谱分析, 构建了抗水分干扰的稳健型基本密度预测模型, 较好地解决了水分含量波动对原料材性快速检测的影响, 为近红外光谱技术在制浆造纸领域的推广应用提供了依据。

关键词: 造纸木片; 近红外光谱; 基本密度; 外部参数正交化算法
中图分类号:O657.3 文献标志码:A
Prediction of Basic Density of Wood Chips Using Near-Infrared Spectroscopy and Moisture Content Correction Algorithm
LIANG Long1,2,3,4, WU Ting1,4,*, SHEN Kui-zhong1, XIONG Zhi-xin5, XU Feng2,*, FANG Gui-gan1,*
1. Institute of Chemical Industry of Forest Products, Chinese Academy of Forestry; Key Lab of Biomass Energy and Material, Jiangsu Province; Co-Innovation Center of Efficient Processing and Utilization of Forest Resources, Jiangsu Province; Key Lab of Chemical Engineering of Forest Products, National Forestry and Grassland Administration; National Engineering Research Center of Low-Carbon Processing and Utilization of Forest Biomass, Nanjing 210042, China
2. College of Materials Science and Technology, Beijing Forestry University, Beijing Key Laboratory of Lignocellulosic Chemistry, Beijing 100083, China
3. Institute of Ecological Conservation and Restoration, Chinese Academy of Forestry, Beijing 100091, China
4. Key Laboratory of Chemistry and Engineering of Forest Products, State Ethnic Affairs Commission, Guangxi Key Laboratory of Chemistry and Engineering of Forest Products, Guangxi University for Nationalities, Nanning 530006, China
5. College of Light Industry and Food Engineering, Nanjing Forestry University, Nanjing 210037, China
*Corresponding authors
Abstract

Wood basic density is an important indicator for assessing the pulping properties of raw wood materials. Rapidly determining the basic density of wood chips using near-infrared spectroscopy (NIRS) can provide basic theoretical data for developing and optimising pulp production processes. However, the source complicacy of raw material leads to high variability within the moisture content of wood chips. These fluctuations in the raw material make it difficult for the NIRS model to give a stable prediction performance. In this paper, the moisture desorption process of poplar chips was dynamically monitored by near-infrared spectroscopy. Principal component analysis (PCA) was applied to distinguish the spectral features due to moisture content to explore the change of free water and bound water in wood fiber. In order to investigate the effect of moisture content on the NIRS prediction of wood density, the partial least square calibration (PLS) models were built using wood chips with different moisture content conditions, respectively. And then external parameter orthogonalization algorithm (EPO) was used to improve the robustness of predictive models by eliminating the influence of chip moisture. The results showed that the best prediction accuracy was obtained from water-saturated chips spectra due to full access to information about fiber structures. However, much water absorption information in the spectra was redundant and useless for modeling, and the variations in moisture content also led to unstable prediction performance. The spectral moisture correction based on EPO was an effective method for desensitizing the calibration model to the influence of moisture content, enabling robust and accurate prediction of basic density. The EPO-PLS model provided a performance with a root mean square error (RMSE) of 12.23 kg·m-3, determination coefficients ( R2) of 0.883 4, and residual prediction deviation (RPD) of 2.93 under different moisture content. This study built a robust NIR calibration model which was robustified against the influence of the variations in moisture content on the wood density prediction. This technology may facilitate the expansion of potential applications of NIR spectroscopy in the paper and pulp industry.

Keyword: Wood chips for the pulp; Near-infrared spectroscopy; Basic density; External parameter orthogonalization algorithm
引言

木材基本密度是造纸原料木片的一项重要材性指标[1]。 在制浆生产中实时监控木片基本密度, 根据原料材性变化合理调整工艺参数, 有助于保证生产线稳定运行。 传统木材密度检测方法对实验条件要求严格、 测试周期长, 无法满足生产线快速批量检测的实际需求。 近红外光谱具有分析速度快、 非破坏性、 测样方式简单灵活等优势, 在木材材性无损检测领域应用前景广阔[2]。 Santos采用近红外技术实现对黑木相思木材基本密度的快速检测[3]。 Alves结合偏最小二乘回归算法建立了预测松木密度的近红外模型, 模型精度能够满足林木育种的应用要求[4]。 Li等通过小波变换优化光谱信号, 提升了近红外模型对榆木密度的预测性能[5]。 还有采用光谱预处理、 特征变量提取和信号采集方式等方面开展模型优化研究, 以提高近红外光谱预测木材密度的精准度和稳定性[6, 7, 8]。

尽管近红外技术检测木材密度的可行性和有效性已被广泛证实, 但这些研究通常是在木材样品水分条件一致的情况下建立密度预测模型。 在制浆造纸行业, 由于原料来源复杂, 采伐、 运输、 存储条件的不同会导致木片水分存在较大差异, 而近红外光谱对样品水分非常敏感, 水分变化引起的光谱差异会严重影响对木材密度的预测。 Fujimoto通过采集样品在不同水分条件下的光谱共同用于建立全局模型, 提高模型的稳健性[9]。 还可在不同水分区间分级独立建模, 调用与待测样品水分一致的模型进行密度预测, 避免水分差异对模型的干扰[10]。 但无论是全局建模还是分级建模, 都需要足够多的建模样品, 增加了模型使用和维护的难度。

外部参数正交化算法(external parameter orthogonalization, EPO)是一种基于正交投影变换的预处理方法, 通过将原始光谱投影到与干扰信息正交的空间中, 消除外部干扰因素的影响[11, 12]。 EPO算法已成功用于消除土壤水分变化对近红外预测有机碳含量的影响, 但在针对木材材性的近红外分析中尚未得到有效应用[13, 14]。 本工作以杨木为研究对象, 探究了水分条件差异对近红外预测木片基本密度的影响。 采用近红外光谱结合主成分分析对木片失水全过程进行解析, 并结合EPO算法计算水分校正因子, 去除光谱中的水分干扰因素, 最终建立抗水分干扰的稳健型基本密度预测模型。

1 实验部分
1.1 样品制备

107速生杨木采自山东省济南市(东经116° 68', 北纬36° 58'), 树龄9年, 平均胸径35 cm。 将杨木试材剥皮后加工成2 cm(纵向)× 2 cm(弦向)× 0.5 cm(径向)木片样品, 共计77个。 首先将所有样品在105 ℃下完全干燥, 记录木片绝干质量W0(kg), 然后将样品在水中浸泡至饱和, 采用排水法测定木片饱水体积V(m3), 木片基本密度B(kg· m-3)为木片绝干质量和饱水体积的比值。

所有样品按照基本密度从小到大排列, 通过间隔取样共挑选17个样品作为EPO水分校正集。 采用Kennard-Stone算法从剩余样品中挑选45个作为训练集, 其余作为测试集。 各样品集统计信息见表1。

表1 样品集基本密度统计信息 Table 1 Statistics of basic density of sample sets
1.2 木片水分实验设计

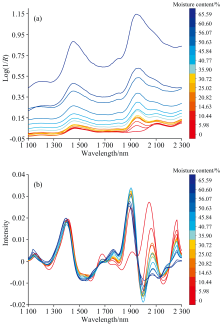
水分校正集: 将饱水木片放入烘箱, 在40 ℃下缓慢烘干并监测水分变化, 当木片水分每降低5%时采集一次近红外光谱组成动态光谱集xm。 当木片水分不再变化, 将烘箱温度升至105 ℃彻底烘干木片并采集绝干木片光谱x0, 最后共采集238条光谱(17个样× 14次)。 木片水分变化情况如图1所示。

图1 木片失水过程Fig.1 Moisture desorption process of wood chips

训练集和测试集: 将饱水木片在恒温恒湿条件下(23 ℃, 50%RH)自然风干, 风干过程中每间隔一定时间采集一次木片近红外光谱并记录水分含量, 共采集360条光谱(60个样× 6次)。 木片风干时间和水分信息见表2。

表2 不同水分条件木片样品制备 Table 2 Preparing process of wood chips with different moisture contents
1.3 近红外光谱采集

使用配备卤素灯光源和光纤探头的光栅光谱仪(NIR2500, 上海复享光学股份有限公司)采集木片近红外光谱, 光谱仪波长范围900~2 500 nm, 波长分辨率为6.3 nm。 采集光谱时, 调整探头距木片表面4 mm, 设置积分时间80 ms, 扫描次数16次, 在木片样品表面随机选择10个测量点采集漫反射信号, 然后取平均值作为该样品原始近红外光谱。

1.4 数据分析

由于原始光谱两端存在严重的噪音和杂散光干扰, 截取1 100~2 300 nm波段用于数据分析。 对光谱进行Savitzky-Golay 卷积平滑、 标准正态变换和一阶导数处理, 以消除基线漂移和表面散射影响。 计算水分校正集的动态差异光谱集D={ x1m- x10, x2m- x20, …, x17m- x170}, 对D进行主成分分析, 研究木片失水过程的光谱特征动态响应。 对不同水分条件下采集的训练集光谱分别建立偏最小二乘回归(partial least square regression, PLS)模型, 对测试集样品基本密度进行预测。 采用均方根误差(root mean square error, RMSE)、 决定系数(determination coefficients, R2)和预测相对标准偏差 (residual prediction deviation, RPD)作为模型预测性能评价指标, 探究木片水分变化对建模性能的影响。

采用EPO算法校正光谱中水分变化信息, 建立EPO-PLS模型, 消除木片水分变化对预测木片密度的影响。 根据EPO算法理论, 原始光谱矩阵X(m× n)可以表示为

X=XP+XQ+R(1)

式(1)中, P(n× n)代表有用信息投影矩阵, 即水分校正因子, Q(n× n)代表干扰信息投影矩阵, R(m× n)为残差矩阵, m是样本数, n是波长点数。

本研究采用水分校正集的失水全过程动态差异光谱集D计算水分校正因子P。

(1)对D的协方差矩阵进行奇异值分解

USVT=svd(DTD)(2)

式(2)中, U(n× n)是左奇异矩阵, S(n× m)是奇异值对角矩阵, V(m× m)是右奇异矩阵。

(2)确定EPO因子数g, 获取V的前g列子矩阵V(m× g), 计算干扰信息投影矩阵Q=Vg VTg。

(3)计算水分校正因子P=I-Q, I是单位矩阵[12]。

(4)对不同水分条件下采集的训练集光谱C和测试集光谱T进行水分校正, C* =CP, T* =TP。 采用校正光谱建立EPO-PLS基本密度预测模型, EPO因子数g和PLS潜变量数Lvs通过留一交叉验证法进行优化。

2 结果与讨论
2.1 木片失水过程的近红外光谱特征研究

木材水分包括自由水和结合水, 其中自由水以液态形式存在于细胞腔中, 而结合水则存在于细胞壁中, 并与细胞壁无定形区中的羟基形成“ 氢键结合” 。 图2(a)是水分校正集样品失水过程原始动态光谱, 随着木片中水分的离去, 所有波长的吸收率呈整体减弱趋势。 对光谱进行预处理后, 基线漂移和谱峰重叠现象得到有效改善, 水分子的OH倍频特征吸收波段(1 850~2 150 nm)发生规律性变化。 随着木片水分降低, 2 100 nm处的特征峰逐渐增强。 由图2(b)可知, 水分变化引起的光谱差异主要集中在1 850~2 150 nm波段, 提取该波段数据进行主成分分析, 结果如图3(a, b, c)所示。 第一主成分得分与水分呈线性相关, 载荷特征峰出现在1 920、 1 980和2 050 nm, 分别对应自由水、 弱氢键结合水和强氢键结合水, 表明第一主成分主要代表木片水分含量的整体变化[15][见图3(a)]。 第二主成分得分随木片失水过程呈现先减小后增大趋势[见图3(b)], 其载荷图[见图3(c)]与结合水相关的特征峰明显强于自由水的峰, 表明第二主成分包含了木材与水的相互作用信息。 根据图3可将木片失水过程分为两个阶段, 第一阶段以自由水离去为主, 第二阶段随着氢键结合被破坏, 束缚在细胞壁中的结合水开始离去, 而失水过程的拐点(30%左右)可用于表征纤维饱和点。 当木材水分高于纤维饱和点时, 水分变化对木材材性影响不大, 低于纤维饱和点时, 木材随水分含量的减少而收缩, 并引起物理力学性能的变化[16]。

图2 木片失水过程光谱变化
(a): 原始光谱; (b): 标准正态变换+一阶导数处理的光谱Fig.2 Spectral changes of chips during the moisture desorption process
(a): Raw spectra; (b): Pre-processed spectra by standard normal variate and first derivative correction

图3 水的OH倍频吸收波段主成分分析
(a): 第一主成分得分; (b): 第二主成分得分; (c): 第一、 第二主成分载荷Fig.3 Principal component analysis of the combination bands of OI from water
(a): The first principal component scores; (b): The second principal component scores; (c): The first and second principal components loadings

2.2 木片水分变化对基本密度预测模型的影响

不同水分条件下建立的基本密度预测模型性能如表3所示。 由于饱水木片最接近木片基本密度实测时的状态, 在此条件下建立的模型M1表现出最好的预测精度, 对测试集的预测均方根误差(RMSEP) 为11.49 kg· m-3, 决定系数 RP2为0.903 0, RPD值达到3.21, 能够满足检测精度需求。 随着木片水分降低, 模型M2和M3的预测性能有所下降, 虽然此时木片水分含量仍在纤维饱和点以上, 木片内部结构状态未受影响, 但由于不同样品失水速率的不同, 水分含量差异增大, 导致光谱数据中水分变异信息增多, 对模型预测造成干扰。 模型M4的预测精度最差, 此时部分样品水分降至纤维饱和点附近, 木片内部自由水和结合水分布状态更加复杂, 木材纤维结构的收缩变化对近红外光的吸收和反射作用造成干扰, 光谱中被引入更多变异信息, 因此模型性能更加不稳定。 而随着木片逐渐风干, 与空气环境的充分接触使木片内部结构和水分分布达到相对平衡状态, 光谱中水分差异信息的减少使模型性能又有所提升。 综上所述, 饱水木片更适合建立基本密度预测模型, 但过高的水分含量导致光谱包含了大量水分冗余信息, 也使模型对样品水分变化更加敏感。 采用模型M1对不同水分条件下采集的测试集光谱进行预测, 结果如图4所示。 模型M1对水分差异大的样品预测均出现不同程度的偏差, 样品水分越低, 预测偏差越大。 因此有必要进行水分校正以消除模型对水分变化的敏感性。

表3 不同水分条件下基本密度预测模型的性能 Table 3 Performances of predictive models for wood density under different moisture content conditions

图4 模型M1对不同水分条件下的测试集预测结果Fig.4 Prediction results of model M1 for the testing samples under different moisture content conditions

2.3 基于水分校正的基本密度预测模型

采用水分校正集的动态差异光谱D计算EPO水分校正因子P, 对饱水木片光谱进行水分校正, 建立EPO-PLS模型, 此外还采用不同水分条件的木片光谱共同建立全局模型作为对照。 图5展示了EPO因子数g和潜变量数Lvs的优化过程。 当g< 3时, 预测精度没有显著变化, 表明此时光谱中的水分干扰信息被扣除并未影响模型预测性能, 最终确定模型g=2, Lvs=3为最优建模参数。

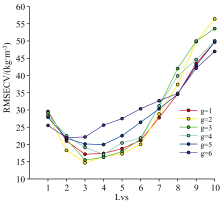图5 不同g和Lvs组合下的模型交叉验证均方根误差图Fig.5 The root mean square error of cross validation from digferent combinations of g and Lvs

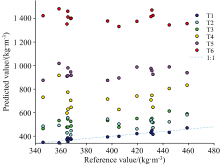
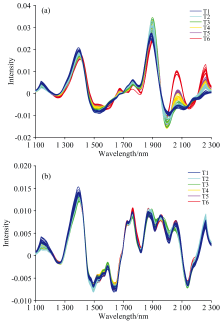
图6(a, b)为EPO水分校正的效果图。 与校正前相比, 1 900~2 100 nm波段水分变化引起的光谱差异被有效消除, 同时在1 500~1 800 nm波段显现出更多特征吸收信息。 EPO-PLS模型的预测性能在表4中列出, 模型表现出与校正水分前相似的交叉验证均方根误差和决定系数, 这表明虽然木片饱水光谱更有利于建模, 但光谱中大量水分特征吸收对预测木片密度是冗余无用的, 有用信息主要来自近红外光与木片纤维结构相互作用所加载的信息。 如图7所示, 不同水分条件下的测试集样品光谱在经水分校正后, 均能够被EPO-PLS模型准确预测, 没有出现显著偏差, RMSEP为12.23 kg· m-3, 决定系数 RP2为0.883 4, RPD为2.93, 表明该模型在预测木片基本密度时对水分变化的干扰具有较强的稳健性, 且预测性能优于全局模型。

图6 不同水分条件下的测试集光谱的EPO水分校正
(a): 水分校正前; (b): 水分校正后水分条件: T1: 61.36~67.62; T1: 44.02~56.57; T1: 38.38~56.11; T1: 26.87~41.32; T1: 19.05~24.23; T1: 9.15~10.06Fig.6 EPO moisture content correction of testing samples under different moisture content conditions
(a): Before moisture content correction; (b): After moisture content correctionMoisture content conditions: T1: 61.36~67.62; T1: 44.02~56.57; T1: 38.38~56.11; T1: 26.87~41.32; T1: 19.05~24.23; T1: 9.15~10.06

表4 水分校正后基本密度预测模型的性能 Table 4 Performances of predictive models for wood density after moisture content correction

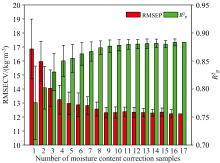
图7 EPO-PLS模型对不同水分条件下测试集预测结果Fig.7 Prediction results of EPO-PLS for the testing samples under different moisture content conditions

2.4 水分校正样品数对EPO-PLS模型的影响

随机抽取不同数量样品计算水分校正因子, 并建立EPO-PLS模型, 每次取样重复10次, 统计模型RMSEP和 RP2的平均值和标准偏差, 结果如图8所示。 当水分校正样品数目较少时, 动态光谱提供的水分变化信息有限, 影响光谱水分校正效果。 而不同样品本身的物理、 化学性质差异也会导致计算结果的不稳定。 随着水分校正样品的增多, 模型的预测精度和稳定性均得到改善。 当每次使用9个样品时, EPO-PLS模型的RMSEP和 RP2分别稳定在12.31 kg· m-3和0.876 5, 10次随机取样建模的标准偏差只有0.38 kg· m-3和0.01, 表明使用9个样品已经能够为计算水分校正因子提供足够的光谱差异信息, 并建立稳定的基本密度预测模型。 此后使用更多样品未能显著提高预测精度, 因此在实际应用中可适当减少水分校正集样品数量, 降低样品制备成本和计算工作量。

图8 水分校正样品数对EPO-PLS模型的影响Fig.8 The effect of the number of moisture content correction samples on EPO-PLS for the prediction of wood density

3 结论

通过对造纸木片失水过程近红外光谱动态监测, 揭示了木片水分中自由水和结合水的变化规律。 通过对不同木片水分条件下建立的基本密度预测模型的性能对比, 发现饱水木

片光谱建立的模型具有最好的预测性能, 但过高的水分含量会导致光谱中无用信息冗余, 对样品水分变化的高敏感度严重影响模型稳定性。 采用EPO算法进行光谱水分校正, 能够在保留光谱中木片密度相关信息的同时, 有效消除水分干扰信息, 建立稳健型的EPO-PLS预测模型。 该模型对样品水分变化具有较强抗干扰能力, 对不同水分含量的样品均表现出较好的预测精度和稳定性, 适用于制浆生产过程中在复杂环境下对原料基本密度的快速检测。

参考文献
[1] SHI Chuan-xi, YU Ying-liang, ZHU Ying-qi, et al(石传喜, 于英良, 朱莹琦, 等). Journal of Forestry Engineering(林业工程学报), 2020, 5(5): 57. [本文引用:1]
[2] FU Rui-yun, ZHANG Wen-bo, LI Dong-qing, et al(符瑞云, 张文博, 黎冬青, 等). Journal of Forestry Engineering(林业工程学报), 2021, 6(2): 114. [本文引用:1]
[3] Santos A, Alves A, Simões R, et al. Journal of Near Infrared Spectroscopy, 2012, 20(2): 267. [本文引用:1]
[4] Alves A, Santos A, Rozenberg P, et al. Wood Science and Technology, 2012, 46: 157. [本文引用:1]
[5] Li Y, Via K, Li Y. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2020, 240(15): 118566. [本文引用:1]
[6] Mora C, Schimleck L, Clark A, et al. Journal of Near Infrared Spectroscopy, 2011, 19(5): 391. [本文引用:1]
[7] YIN Shi-kui, LI Chun-xu, MENG Yong-bin, et al(尹世逵, 李春旭, 孟永斌, 等). Journal of Central South University of Forestry & Technology(中南林业科技大学学报), 2020, 40(5): 171. [本文引用:1]
[8] Diesel K, Costa F, Pimenta A, et al. Wood Science and Technology, 2014, 48: 949. [本文引用:1]
[9] Fujimoto T, Kobori H, Tsuchikawa S. Journal of Near Infrared Spectroscopy, 2012, 20(3): 353. [本文引用:1]
[10] Liang L, FangG, Deng Y, et al. Forest Science, 2019, 65(5): 548. [本文引用:1]
[11] Hans G, Allison B. Journal of Near Infrared Spectroscopy, 2019, 27(4): 259. [本文引用:1]
[12] Roger J, Chauchard F, Bellon-Maurel V. Chemometrics and Intelligent Laboratory Systems, 2003, 66(2): 191. [本文引用:2]
[13] LI Shuo, LI Chun-lian, CHEN Song-chao, et al(李硕, 李春莲, 陈颂超, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(4): 1234. [本文引用:1]
[14] Minasny B, McBratney A, Bellon-Maurel V, et al. Geoderma, 2011, 167: 118. [本文引用:1]
[15] Ma T, Schimleck L, Inagaki T, et al. Holzforschung, 2021, 75(4): 345. [本文引用:1]
[16] Huang C, Chui Y, Gong M, et al. Journal of Bioresources and Bioproducts, 2020, 5(4): 266. [本文引用:1]