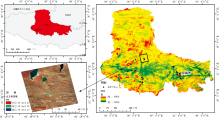
藏北高原位于西藏自治区北部、 唐古拉山脉、 念青唐古拉山脉和岗底斯之间。 选择具有显著砾石特征的那曲地区为实验数据的主要采集点(图1)。 那曲地区作为青藏高原的中心地带, 地势呈现了南北高、 中间低的特点, 绝大部分地区的海拔分布在4 000~5 100 m之间。 地貌类型由东、 中、 西三个区构成, 即为高山深谷、 高山宽谷和高原湖盆区。 实验区主要有四大土壤类型, 分别是高山草甸土、 亚高山草甸土、 高山荒漠草原土、 高山草原土。 高山草甸土多砾石, 部分区域的土壤砾石覆盖度在5%~30%之间; 亚高山草甸土草根层结构较为紧密, 其腐殖质层也较厚; 高山草原土是藏北高原主要土壤类型, 主要分布于申扎、 班戈、 尼玛和双湖县南部, 有很多石粒, 石灰反应较强; 高山荒漠草原土地地面物质粗, 有机质含量低且土层薄, 在尼玛县和双湖县北部区域较为常见。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 野外采样点示意图Fig.1 Schematic diagram of field sampling points

1.2.1 野外实验设计

在不同的海拔梯度进行样带的布设, 一个样带包括五个样区, 每个样区是30 m× 30 m的, 每个样区包括8个50 cm× 50 cm的测量样方。 其中有4个砾石样方、 2个植被样方和2个土壤样方, 每个砾石样方选取4~6块砾石测量其粒径与光谱数据。 为保障光谱测量时所需要的光照条件, 特选取藏北高原地区光照条件良好的7月— 8月来进行野外实测数据的采集, 选择在地表砾石特征显著、 地势开阔平缓的地区进行测定。

使用便携式光谱辐射计(SVC HR-1024)测量单个砾石的冠层光谱、 砾石的群落光谱, 土壤的群落光谱及植被的群落光谱。 光谱范围是350~2 500 nm, 涵盖了可见光到短波红外波段, 总共有1 024个光谱波段。 光谱测定对光照条件的要求较高, 所以要在天气晴朗的情况下测量, 同时风力对采集光谱也有一定的影响, 有风的天气不作为采集窗口。 采用两个步骤来获取砾石的群落光谱(样方内光谱值)和冠层光谱(单一物体光谱值), 先对白板进行测量校正光谱仪, 测量时将传感器探头垂直向下对准样方, 距离样方80 cm进行三次群落光谱测量, 三次测量取均值。 然后再对单个砾石进行测量, 每个砾石测量3次光谱, 取其平值作为砾石冠层光谱值。

为分析每个样方中的砾石粒径与其光谱曲线之间的关系, 在测量砾石的群落光谱时, 一并记录了每个砾石样方的覆盖度高低, 并在每个样方中选取了8块砾石用游标卡尺测量其单个砾石的Feret直径, 包括最大Feret直径与最小Feret直径; 后期的处理中选取了4~6块砾石进行砾石粒径的计算, 以估算整个样方中砾石的粒径数据。

1.2.2 高光谱数据处理

1.2.2.1 高光谱地面数据处理

实测高光谱数据在1 900 nm波段附近, 大气中的水汽吸收对光谱测量产生了极大的干扰^{[15, 10]}, 砾石的反射率变化剧烈, 数据质量差, 对于数据分析有极大的干扰。 通过对所有野外光谱数据的比较分析, 发现在980 nm附近的反射率数据出现了折返现象, 2 350~2 500 nm范围内的光谱数据由于仪器自身原因, 波段信息极不稳定, 数据波动明显。 由此将受水汽吸收影响严重的波段以及信息极不稳定的波段的光谱数据进行剔除, 即将964~1 010, 1 850~2 000和2 450~2 500 nm范围内的光谱数据进行剔除。 原始数据使用Savitzky-Golay卷积平滑算法^[11], 利用多项式最小二乘法拟合移动窗口中的数据, 计算出窗口中心点与周围点之间的加权平均数进行光谱滤波, 以达到去除噪声的效果。

采用了导数光谱变换提取原始光谱R中的隐含信息, 进行以下9种光谱变换: 一阶导数(R')、 二阶导数[(R')']、 倒数 1R、 倒数的一阶导数 1R'、 对数(Lg(R))、 对数的一阶导数((Lg(R))')、 对数的倒数 1Lg(R)、 对数的倒数的一阶导数 1Lg(R)'、 平方根的一阶导数 R'。 砾石的原始光谱反射率经过 1R, Lg(R), 1Lg(R)三种变换后, Y值随波长的变化, 有着较为明显的线性关系。 而经过一阶导数变换后, 可以看出原始光谱曲线中不能观察到的信息。 较为明显的峰值区间, 能更好的凸显样品的吸收和反射特征。

1.2.2.2 高光谱图像

高分五号卫星携带的可见光短波红外高光谱相机(advanced hyper spectral imager, AHSI)所获取的高光谱影像, 光谱覆盖范围从可见光到短波红外波段(390~2 500 nm), 总计有330个有效波段。 本研究中采用的AHSI高光谱影像是通过高分辨率对地观测系统网格平台(国家航天局对地观测与数据中心、 https://www.cheosgrid.org.cn/)获得。 高分五号高光谱数据是通过对观测数据(L0级)进行预处理和辐射校正得到的辐亮度数据(L1级)。 L1级数据是在L0级数据之上经过辐射校正、 坏像元修复、 光谱校正、 SWIR多个传感器的观测数据拼接以及生成观测几何参数所得到的。 通过上述的步骤之后L1级数据将不会有坏的像元或是其他误差。 在使用高光谱影像对砾石粒径反演之前, 对获取的影像数据进行辐射定标、 大气校正和正射校正等操作。

1.2.3 砾石数据处理

为测量砾石的粒径, 每个样方中用游标卡尺测量8块砾石的最大Feret直径与最小Feret直径。 Feret直径计算公式如式(1)

DF=(Mmin2+Mmax2)12(1)

式(1)中, D_F代表的是砾石粒径, M_min代表最小Feret直径, M_max最大Feret直径。 测量结果显示砾石的粒径分布在10~120 mm之间。 通过调查每个样方中的砾石覆盖度, 以确定每个测量样方的砾石覆盖度, 以便后续建立砾石样方的群落光谱与砾石覆盖度之间的反演模型。

根据Wentworth提出的砾石分级理论将采集的砾石粒径分为4个等级。 粒径在8~16 mm的砾石分为中砾, 粒径在16~32 mm之间的砾石分为粗砾, 粒径在32~64 mm之间的分为极粗砾, 粒径在64~256 mm之间的砾石分为卵石。 砾石分级如表1所示。

表1

Table 1

表1(Table 1)

表1 砾石粒径分级表[12] Table 1 Classification of gravel particle size[12] 粒径范围 类别名称 > 256 mm 巨砾/漂石 64~256 mm 卵石 32~64 mm 极粗砾 16~32 mm 粗砾 8~16 mm 中砾 4~8 mm 细砾 2~4 mm 极细砾

表1 砾石粒径分级表[12] Table 1 Classification of gravel particle size[12]

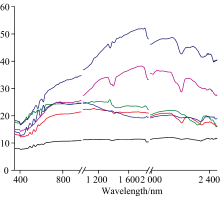
由于采集到砾石粒径主要集中在粗砾和极粗砾之间, 故本次利用高光谱遥感对砾石粒径的反演主要采用粒径在17~67 mm之间的砾石来进行。 实测砾石的光谱见图2。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 实测砾石的光谱Fig.2 Spectra of gravels

1.3.1 相关系数法

相关系数是由统计学家Karl Pearson所设计的统计量, 用于研究变量之间线性相关的统计指标, 通常用R表示。 在进行砾石粒径与导数光谱变换的相关性分析中, 拟将测得数据按照海拔梯度的变化来进行数据的划分, 并对每一个海拔梯度的数据根据Wentworth砾石分级理论来进行粒径分级。 采用相关系数法, 按照波长的顺序对每个波段与砾石粒径之间的相关性进行分析。 相关系数法的数学表达如式(2)所示

γi=Cov(R, L)D(R)D(L)=∑i=1N(Rni-R-i)(Ln-L-)∑i=1N(Rni-R-i)2∑i=1N(Ln-L-)2(2)

式(2)中, γ _i为每一个波段与砾石粒径之间的相关性系数, i是波段序号, γ _i取值范围是(-1, +1)。 γ _i越接近+1(-1), 二者之间的相关称度越高, 接近+1是正相关, 反之, 接近-1是负相关。 R_ni表示的是第n个砾石的第i个波段的光谱反射值, R-表示的是N个砾石在第i波段处的光谱反射率均值, L_n表示的是第n个砾石的粒径值, L-表示的是N个砾石的均粒径值, N表示的是砾石总数。

1.3.2 建模方法

逐步回归模型是被应用于多元线性统计模型中最为常见的回归模型。 该模型引入许多可变的因素方量作为独立变量来预测变量, 但引入中有不少变量是无意义的, 或者引起存在差异性问题, 只有将不切实际的或矛盾的因素删除, 变量和变量之间的联系才能建立的更加准确。 逐步回归技术包含3种实现方式: 前向技术、 后向技术, 因此也包括交替技术。 前向技术从一个指示变量开始, 一点点地引入新的指示变量。 而后向技术则相反, 事先将所有自由变量纳入到指令变量集中, 逐一消除了不显著的变量。 交替技术可以是二者的结合, 在引入变量和消除变量之间轮换使用, 直至没有新的解释变量被引入, 也没有无关紧要的变量被消除。

1.3.3 模型精度评价

为确保反演模型的精确性与使用性, 采取交叉验证的方法来评价模型的预测结果, 选取了相对误差(RE)、 均方根误差(RMSE)和决定系数(R²)三个指标因子来比较不同的砾石粒径模拟模型。 相应的计算如式(3)和式(4)所示

RMSE=1n∑i=1n(zi-zi* )2(3)

RE(%)=1n∑i=1n|zi* -zi|zi×100%(4)

式(3)和式(4)中, z_i为砾石粒径的观测值, zi*为砾石粒径的拟合值, n为样本数量, RMSE的值和RE的值越小, 标志着该拟合模型的结果越好。

2.1.1 基于光谱导数变换的砾石粒径与反射率光谱的模型

将9种不同形式的导数变换后的光谱值与砾石粒径进行相关性分析, 可以知道反射率光谱与砾石粒径之间存在着较为显著的相关性(表2), 砾石粒径与经过光谱变换后的某一波段光谱值在0.01水平上有显著的相关性。 与砾石粒径相关性最高的是910.5 nm处的波段。 通过不同形式的光谱导数变换后可以看出与砾石粒径呈现正相关且相关性最高的是经过一阶导数变换的371.5 nm波段(r=0.515), 一阶导数变换后的910.5 nm波段的光谱值和砾石粒径呈现负相关(r=-0.531)。 平方根的一阶导数变换后在369.9 nm处与砾石粒径呈现正相关关系, 在910.5 nm处和砾石粒径呈现负相关。 采用逐步回归法, 将敏感性高的波段与砾石粒径建立反演模型。

表2

Table 2

表2(Table 2)

表2 不同形式的光谱导数变换后反射率与砾石粒径相关系数 Table 2 Correlation coefficients between reflectance and gravel grain size based on different spectral derivative transformations 一阶导数 r 平方根的一阶导数 r 371.5 0.515 369.9 0.510 910.5 -0.531 910.5 -0.523

表2 不同形式的光谱导数变换后反射率与砾石粒径相关系数 Table 2 Correlation coefficients between reflectance and gravel grain size based on different spectral derivative transformations

2.1.2 模型反演能力评价

依据回归决定系数(R²)最大、 均方根误差(RMSE)最小和F统计量最高的原则, 对建立的砾石粒径模拟模型进行对比挑选。 通过表3显示的结果得知, 光谱曲线经过一阶导数变换后的910.5 nm波段处的反射率数据与砾石粒径建立的回归模型的效果相较于其他形式的光谱变换的回归模型的结果是最佳的。 主要是由于光谱曲线经过一阶导数变换后, 将原始光谱曲线中的隐含信息进行了更加明显的表达, 增强砾石表面的光谱信息, 为预测砾石粒径提供了更加可靠的信息。

表3

Table 3

表3(Table 3)

表3 砾石粒径回归模型参数分析 Table 3 Parameter analysis of gravel particle size regression model 光谱变换形式 F统计量 决定系数 (R2) 均方根误差 (RMSE) 系数检验 一阶导数 910.5 279.75 0.738 4.702 p< 0.001 一阶导数 371.5 190.82 0.697 5.015 p< 0.001 平方根的一阶导数 910.5 219.14 0.721 5.20 p< 0.001 平方根的一阶导数 369.9 150.19 0.66 4.328 p< 0.001

表3 砾石粒径回归模型参数分析 Table 3 Parameter analysis of gravel particle size regression model

图3和图4是原始光谱经过一阶导数变换和平方根的一阶导数变换在不同波段的光谱值与砾石粒径的散点图。 以上四幅散点图显示, 经过不同形式的光谱变换后, 砾石粒径大小与反射率之间的相关性得到了不同程度的增强。 通过一阶导数变换可以将光谱中的隐含信息得到表达, 也可以将一些背景信息隐去, 为建立砾石粒径与反射率数据的回归模型提供更精确的指标。 综上所述, 在本研究中对光谱曲线进行不同形式的光谱变换时十分有必要的, 通过不同形式的光谱变换, 可以更加精确的建立砾石粒径与光谱反射率之间的回归模型。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 一阶导数变换光谱与砾石粒径散点图Fig.3 Scatter plots of first-order derivative transformed spectra and gravel particle size at 371.5 and 910.5 nm

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 平方根一阶导数变换光谱与砾石粒径散点图Fig.4 Scatter plots of square root first order derivative transformed spectra and gravel particle size at 371.5 and 910.5 nm

2.2.1 砾石粒径与光谱吸收指数的模型

利用光谱连续统去除对野外实测砾石光谱数据进行归一化处理, 可以看出不同粒径大小砾石之间的光谱差异。 图6是连续统去除后砾石的光谱曲线。 与原始的光谱(图5)比较发现, 砾石之间先前较为微弱的吸收峰得到了增强, 可以看出其间的差异。 仔细观察经过连续统去除后的光谱(图6)可以看出(图6), 不同粒径大小的砾石在1 410、 2 210和2 340 nm附近的波段区间有着较为明显的光谱吸收特征, 且不同粒径大小的光谱吸收特征也差异较大。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同粒径大小砾石的光谱反射率曲线图Fig.5 Spectral reflectance curves of gravels with different particle sizes

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同粒径大小砾石连续统去除后光谱曲线图Fig.6 Continuum removed spectra of gravels with different particle sizes

将具有明显吸收特征区间内的光谱特征指数[吸收波波长位置(λ )、 宽度(W)、 深度(H)、 吸收对称度(d)、 吸收面积(A)]进行提取, 并利用这些指数分别与砾石的粒径值进行相关性分析, 建立遥感反演模型。 选择了6个与砾石粒径相关度高的光谱因子, 对砾石粒径进行模拟分析。 建立的砾石粒径模拟模型中, 其p值都满足p< 0.001的条件。

通过上述的光谱吸收特征指数与砾石粒径的相关性分析与下文中展示的砾石粒径与各光谱吸收特征指数的散点图, 可以明显看出砾石粒径与光谱吸收特征指数之间的关系: (1)在2 340 nm波段附近计算得到的光谱吸收深度(H)与砾石粒径有着极强的相关性关系(r=0.505, 表4), 使用砾石粒径与其建立回归模型后其决定系数R²=0.734(图9), 表明砾石粒径在17~60 mm这个区间, 随着砾石粒径的增大, 其光谱的吸收深度也是逐渐增大的, 具有较为明显的正向相关关系。 该光谱吸收区间内的吸收面积(A)与砾石粒径之间存在着负相关关系, 表明砾石粒径增大, 在该区间内的吸收面积反而减小。 (2)在1 410 nm波段附近计算所得的光谱吸收面积(A)同样也存在着砾石粒径的增大(图7), 光谱吸收面积增大的正向相关关系, 其关系在砾石粒径在17~30 mm范围内得到的较好的体现, 砾石粒径大于30 mm后预测的砾石粒径值与测量的砾石粒径值之间的残差较大。 (3)在2 210 nm波段附近计算的光谱吸收深度(H)与光谱吸收面积(A)与砾石粒径之间都存在着正相关性关系(图8)。 吸收深度(H)和吸收面积(A)与砾石粒径存在着正向相关关系, 光谱吸收深度的相关性高于光谱吸收面积的相关性, 然而他们对于某一粒径范围内的砾石的预测值的残差较大, 拟合效果不佳。

表4

Table 4

表4(Table 4)

表4 光谱吸收特征指数与砾石粒径相关性参数 Table 4 Correlation parameters between spectral absorption characteristic index and gravel particle size 1 410 nm 2 210 nm 2 340 nm 吸收 深度 (H) 吸收 面积 (A) 吸收 深度 (H) 吸收 面积 (A) 吸收 深度 (H) 吸收 面积 (A) 相关系数 (r) 0.501 0.487 0.493 0.472 0.505 -0.503

表4 光谱吸收特征指数与砾石粒径相关性参数 Table 4 Correlation parameters between spectral absorption characteristic index and gravel particle size

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 1 410 nm附近吸收面积与吸收深度与砾石粒径散点图Fig.7 Scatter plots of absorption area and absorption depth vs. gravel particle size near 1 410 nm

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 2 210 nm附近吸收面积与吸收深度与砾石粒径散点图Fig.8 Scatter plots of absorption area and absorption depth vs. gravel particle size near 2 210 nm

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 2 340 nm附近吸收面积与吸收深度与砾石粒径散点图Fig.9 Scatter plots of absorption area and absorption depth vs. gravel particle size near 2 340 nm

上述的相关性分析表明砾石粒径与其自身的光谱吸收特征指数之间存在着定性与定量的关系。 所以根据上述的两者的分析, 采用逐步回归分析建模回归模型。 其回归方程如式(5)— 式(10)所示:

1 410 nm附近光谱吸收特征区间回归方程式

Y=19.60+0.6287×A1410-0.00043×A14102(5)

Y=18.09+93.91×H1410+8.79×H14102(6)

2 210 nm附近光谱吸收特征区间回归方程式

Y=24.26+0.5311×A2210+0.008114×A22102(7)

Y=15.78+149.9×H2210-96.09×H22102(8)

2 340 nm附近光谱吸收特征区间回归方程式

Y=63.36-1.376×A2340+0.007815×A23402(9)

Y=22.36+57.29×H2340+72.75×H23402(10)

以上的回归方程中, H_{1 410}和A_{1 410}分别代表砾石在1 410 nm波段附近的光谱吸收深度和光谱吸收面积; H_{2 210}和A_{2 210}分别代表砾石在2 210 nm波段附近的光谱吸收深度与光谱吸收面; A_{2 340}和H_{2 340}别代表砾石在2 340 nm波段附近的光谱吸收深度和光谱吸收面积。

2.2.2 模型反演能力评价

采用均方根误差(RMSE)、 决定系数(R²)和F统计量对每一个回归方程进行评价, 并选出效果最好的回归方程。 评价原则是决定系数(R²)和F统计量最高且均方根误差(RMSE)最小。 依据此原则在2 430 nm波段附近的光谱吸收区间内的吸收深度(H)与砾石粒径建立的回归模型能更好的体现出砾石粒径与光谱吸收指数之间的关系(表5)。

表5

Table 5

表5(Table 5)

表5 光谱吸收指数与砾石粒径回归方程参数 Table 5 Parameters of the regression equation of spectral absorption index and gravel particle size 光谱吸收指数 光谱吸收区间 F统计量 RMSE R2 吸收深度(H) 吸收面积(A) 1 410 nm 206.42 188.07 4.564 4.825 0.721 0.697 吸收深度(H) 吸收面积(A) 2 210 nm 177.66 145.83 5.694 5.694 0.712 0.679 吸收深度(H) 吸收面积(A) 2 340 nm 266.39 230.24 5.015 6.220 0.734 0.728

表5 光谱吸收指数与砾石粒径回归方程参数 Table 5 Parameters of the regression equation of spectral absorption index and gravel particle size

采用了两种不用的方法来进行遥感反演。 一是对原始光谱曲线进行不同形式的光谱变换, 然后逐波段与砾石粒径进行相关性分析, 将跟砾石粒径敏感度最高的波段选出, 将选取的敏感波段与砾石粒径进行遥感回归模型的建立。 二是利用光谱的连续统去除技术扣除基线等, 找出砾石的光谱吸收特征区间, 计算各光谱吸收特征区间内的光谱吸收特征指数, 并与砾石粒径进行相关性分析, 选取出具有显著相关性的光谱吸收指数来建立回归模型。

两种砾石粒径遥感反演建立了不同的回归模型。 利用光谱变换法建立的最佳模型Y=41.29-1 054× b910.5+9 600× b910.5², 利用连续统去除法建立的回归模型是Y=22.36+57.29× H_{2 340}+72.75× H23402。 对比两种回归模型的决定系数(R²)以及均方根误差(RMSE), 认为采用导数的光谱变换来建立的砾石粒径拟合回归模型的是比较好的, 该模型在对于粒径范围在17~67 mm之间的砾石粒径的预测是比较好的, 因此使用高光谱吸收指数对砾石粒径的最佳预测模型是: Y=41.29-1 054× b910.5+9 600× b910.5²。

研究中发现原始光谱曲线与砾石粒径之间的相关性, 将光谱数据进行了不同形式的光谱变换, 再次与砾石粒径进行相关性分析, 寻找相关性程度最高的波段与砾石粒径进行回归分析, 建立了光谱敏感波段与砾石粒径的回归模型。 其次是将光谱曲线进行连续统去除, 分析砾石粒径与各光谱吸收特征之间的关系, 然后建立了光谱吸收指数与砾石粒径之间的回归模型。 通过对这两种类别的回归模型进行对比分析, 选择出最佳预测砾石粒径的回归模型。 图10是敏感波段与光谱吸收指数两种不同的最佳回归模型对比图。 图10左图是原始光谱曲线经过一阶导数变换后在910.5 nm出的反射率与砾石粒径的散点图; 右是连续统去除后在2 340 nm附近的光谱吸收深度与砾石粒径的散点图。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 两类回归模型散点图对比Fig.10 Comparison of scatter plots of two types of regression models

经过一阶导数变换的敏感波段与砾石粒径的回归模型和连续统去除后在2 340 nm出的光谱吸收深度与砾石粒径的回归模型分别是两种形式的砾石粒径回归模型中最佳的。 通过这两种最佳回归模型的对比分析发现。 敏感波段与砾石粒径建立的回归分析模型的F统计量是279.75, RMSE是4.702, 决定系数是0.738; 光谱吸收深度与砾石粒径的回归分析模型的F统计量是266.39, RMSE是5.105, 决定系数是0.734。 通过导数光谱变换选取的敏感波段建立的砾石粒径拟合模型效果是最佳的, 是最能准确预测砾石粒径的回归模型。 其回归分析模型如式(11)所示

Y=41.29-1054×b910.5+9600×b910.52(11)

该回归模型对砾石粒径的预测效果较好的条件是砾石的粒径分布在17~67 mm之间, 依据此回归模型结合高分五号AHSI高光谱影像计算出砾石粒径的空间分布(图11)。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 砾石粒径空间分布图Fig.11 Spatial distribution of gravel particle size

将模型得到的最佳反演的砂石粒径空间分布与野外实测的砂石粒径值进行比较, 我们发现, 利用高分五号AHSI高光谱影像来对该地区的砾石粒径进行定量反演, 其精度能达到70%, 造成误差的主要原因是由于高光谱影像包含的光谱信息较多, 存在着混合像元的现象, 所以进行砾石粒径的空间反演是会与野外实测的砾石粒径存在差异。 虽然对野外实测光谱数据进行的导数变换和连续统去除、 高光谱影像数据进行大气校正等处理获取了地物的真实反射率数据, 剔除了部分背景因素的影响, 但是由于高光谱数据的冗余和其他因素的存在, 再进行定量反演依然会存在一定的误差。

图12显示该区域的砾石粒径主要在37~43 mm, 其中粒径在39.8~40.4 mm的区域是最多的, 占比面积达到70%, 其在该研究区的分布地域也最为广泛。 通过砾石粒径的空间分布图与野外调查结果分析得知, 在道路周围的砾石粒径较大且存在砾石较多, 主要是由于道路两侧受到的人工干扰较大。 以及在湖泊周围的砾石粒径是比较大的。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 研究区粒径统计图Fig.12 Grain size statistics in the study area