遗传算法和连续投影算法结合的土壤有机碳含量高光谱估算模型

引用本文

牛芳鹏, 李新国, 白云岗, 赵慧. 遗传算法和连续投影算法结合的土壤有机碳含量高光谱估算模型[J]. 光谱学与光谱分析, 2023,43(7): 2232-2237.
NIU Fang-peng, LI Xin-guo, BAI Yun-gang, ZHAO Hui. Hyperspectral Estimation Model of Soil Organic Carbon Content Based on Genetic Algorithm Fused With Continuous Projection Algorithm[J]. Spectroscopy and Spectral Analysis, 2023,43(7): 2232-2237.
Doi:10.3964/j.issn.1000-0593(2023)07-2232-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

遗传算法和连续投影算法结合的土壤有机碳含量高光谱估算模型

牛芳鹏^1,², 李新国^1,^3,^*, 白云岗², 赵慧⁴

1.新疆师范大学地理科学与旅游学院, 新疆乌鲁木齐 830054

2.新疆水利水电科学研究院, 新疆乌鲁木齐 830049

3.新疆干旱区湖泊环境与资源实验室, 新疆乌鲁木齐 830054

4.新疆财经大学统计与数据科学学院, 新疆乌鲁木齐 830012

*通讯作者 e-mail: onlinelxg@sina.com

作者简介: 牛芳鹏, 1995年生,新疆水利水电科学研究院助理工程师 e-mail: niufp0225@163.com

收稿日期: 2022-04-01 修回日期: 2022-07-24

基金: 国家自然科学基金项目(41661047),新疆维吾尔自治区重大科技专项(2020A01022-1)资助

摘要

土壤有机碳含量是土壤肥力与土壤质量的主要决定因素, 与土壤生产力密切相关。采用高光谱模型估算土壤有机碳含量成为了解土壤肥力的重要方法。利用高光谱分析技术结合机器算法实现快速、高精度的估算土壤有机碳含量, 对土壤肥力的可持续利用至关重要。根据实测的土壤有机碳含量及其高光谱反射率数据, 运用Savitzky Golay方法对光谱波段进行平滑去噪, 采用连续投影算法(SPA)、遗传算法(GA)对原始光谱及其5种不同数学变换光谱分别进行特征波段的筛选, 并基于随机森林(RF)方法构建土壤有机碳含量的高光谱估算模型。为进一步降低模型的复杂度, 将SPA算法与GA算法相结合, 寻找最佳特征参数, 以提升土壤有机碳含量特征波段的识别率和可信度。结果表明: (1)在原始光谱中, 基于GA算法筛选SOC含量的高光谱响应波段主要集中在350~410、 827~928、 997~1 064、 1 201~1 234、 1 541~1 574、 1 667~1 710、 2 153~2 186和2 357~2 707 nm; 当RMSE为6.09时, SPA算法筛选了11个特征变量。 (2)基于GA算法筛选特征波段时, 原始光谱R、标准正态变量(SNV)、多元散射校正(MSC)、一阶微分(FD)、对数的倒数(RL)与连续统去除(CR)的维数分别降低到407、 697、 668、 667、 493、 784维, 占全光谱波段的18.93%~36.47%; 基于GA-SPA算法筛选后, 6种光谱变量的维度介于8~17维, RMSE介于4.53~6.30。 (3)在一阶微分光谱形式下, 基于GA-SPA算法挑选的12个特征变量所构建的RF模型预测效果最好, 模型的建模集Rc2为0.78, RMSE_c为5.48, 验证集Rp2为0.82, RMSE_p为4.50, RPD为2.18。研究表明, 光谱一阶微分可以增强土壤的光谱信息, GA算法结合SPA算法寻找光谱特征变量, 既简化了估算模型的复杂度, 又提高了估算模型的精度, 基于遗传算法—连续投影算法的高光谱模型具有较高的估算能力。

关键词: 土壤有机碳含量; 连续投影; 遗传算法; 高光谱估算模型; 湖滨绿洲

中图分类号:S153.6 文献标志码:A

Hyperspectral Estimation Model of Soil Organic Carbon Content Based on Genetic Algorithm Fused With Continuous Projection Algorithm

NIU Fang-peng^1,², LI Xin-guo^1,^3,^*, BAI Yun-gang², ZHAO Hui⁴

1. College of Geographic Sciences and Tourism, Xinjiang Normal University, Urumqi 830054, China

2. Xinjiang Institute of Water Resources and Hydropower Research, Urumqi 830049, China

3. Xinjiang Laboratory of Lake Environment and Resources in Arid Zone, Xinjiang Normal University, Urumqi 830054, China

4. School of Statistics and Data Science, Xinjiang University of Finance and Economics, Urumqi 830012, China

*Corresponding author

Abstract

Soil organic carbon content was a major determinant of soil fertility and soil quality and was closely related to soil productivity. The estimation of soil organic carbon content using hyperspectral models has become an important method of understanding soil fertility. Using hyperspectral analysis combined with machine algorithms to achieve rapid and highly accurate estimation of soil organic carbon contents was essential for the sustainable use of soil fertility. Using the measured soil organic carbon content and its hyperspectral reflectance data as the research object, we applied the Savitzky Golay method to smooth and demise the spectral bands, used successive projection algorithm (SPA) and genetic algorithm (GA) to screen the original spectra and its five different mathematical transformed spectra respectively for the characteristic bands, and constructed the random forest (RF) method based on the soil organic carbon content. The hyperspectral estimation model of soil organic carbon content was constructed using the random forest (RF) method. The SPA algorithm was combined with the GA algorithm to find the optimal feature parameters to improve the recognition rate and confidence in the SOC feature bands. The results showed that in the original spectrum, the hyperspectral response bands based on the GA algorithm to screen SOC content were mainly concentrated on 350~410, 827~928, 997~1 064, 1 201~1 234, 1 541~1 574, 1 667~1 710, 2 153~2 186, 2 357~2 707 nm. When the RMSE was 6.09, 11 characteristic variables were screened by the SPA algorithm. The dimension of the original spectrum, standard normal variables (SNV), multiple scattering corrections (MSC), first-order differential (FD), logarithmic reciprocal (RL) and continuum removal (CR) were reduced to 407, 697, 668, 667, 493 and 784 dimensions respectively, accounting for 18.93%~36.47% of the full spectral band when filtering the characteristic bands based of the GA algorithm. After screening based on the GA-SPA algorithm, the dimensions of the six spectral variables ranged from 8 to 17 dimensions, and the RMSE ranged from 4.53 to 6.30. In the first-order differential spectral form, the RF model constructed based on 12 feature variables selected by the GA-SPA algorithm predicted the best results from a modeling setRc2 of 0.78 and RMSE_c of 5.48, a validation setRp2 of 0.82, RMSE_p of 4.50, and RPD of 2.18. It was shown that the first-order spectral differentiation could enhance the spectral information about soil, the GA algorithm combined with the SPA algorithm to find the spectral feature variables simplifies the complexity. It improves the accuracy of the estimation model, and the hyper spectral model based on the genetic algorithm-continuous projection algorithm has a high estimation capability.

Keyword: Soil organic carbon content; Successive projection algorithm; Genetic algorithm; Hyperspectral estimation model; Lakeside oasis

文章图片

引言

土壤有机碳(soil organic carbon, SOC)在促进植物的生长和发育、改良土壤物理性质方面发挥着重要的作用, 是土壤碳库的重要组成部分。在西北干旱地区, 关于土壤有机碳的研究, 对推进绿洲农业发展与“土壤碳循环”具有重大作用与意义^[1]。关于SOC含量的研究早期都是通过经验模型法估算的, 不涉及机理过程问题, 较易实现, 但受人为因素和区域尺度影响较大。随着高光谱遥感技术的发展, 土壤反射光谱成为一种快速、高效的土壤属性估算方法, 学者们关于光谱信息的预处理^[2]、特征变量选择^[3]、建模手段^[4]等方面做了大量的研究。 Moura-Bueno等采用导数、归一化和非线性变换等六种预处理技术与偏最小二乘、多元线性回归、支持向量机和随机森林算法(random forest, RF)四种多元校正方法以确定预测SOC含量的最佳组合^[5]。 Wang等分析了澳大利亚东部半干旱牧场的SOC库存, 采用逐步回归和遗传算法(genetic algorithm, GA)来选择信息量最大的变量, 然后使用这些选定的预测变量来训练增强回归树和RF模型, 结果表明GA-RF能够可靠的预测SOC储量, 其构建的模型RMSE为7.44, R²为0.48^[6]。肖艳等采用小波变换和连续投影算法(successive projection algorithm, SPA)挑选黑土SOC含量光谱特征波段, 其构建的支持向量机模型建模集R²由土壤全谱的0.75提升至第3层小波低频系数的0.91, RMSE由7.46降低至4.12^[7]。目前, SOC含量特征波段的提取主要采用逐步回归、相关系数法或SPA等单一方法, 易受到外部环境的影响, 不能敏感的反映土壤光谱信息。如何将不同分类模型组合并应用于光谱信息的识别中, 并与机器算法结合提高模型精度逐渐成为一种高效的手段。为减少光谱信息重叠, 采用GA算法对预处理后的光谱数据进行特征波段筛选后, 结合SPA算法进一步寻找最佳特征参数, 以提升SOC含量特征波段的识别率, 最后利用RF方法建立基于特征波段的GA-SPA-RF土壤有机碳含量模型, 以期能够为准确地定量估算湖滨绿洲土壤有机碳含量提供基础支撑。

1 实验部分

1.1 研究区概况

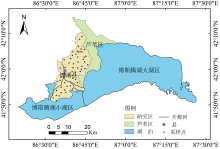
博斯腾湖西岸湖滨绿洲位于新疆焉耆盆地, 地理位置介于86°30'—86°50'E, 4l°33'—42°14'N, 海拔1 047~1 048 m。天气寒冷和干燥, 年均气温为9.0 ℃, 夏季月均温22.8 ℃, 冬季月均温9.0 ℃, 年平均降水量为83.60 mm, 地下水可利用量为9.05×10⁸ m³·a^-1, 矿化度为0.10~10.00 g·L^-1。研究区植被主要以胡杨、芦苇等为主, 土壤类型主要以草甸土与盐渍土为主。

	Figure Option View Download New Window
	图1 研究区位置图Fig.1 Location map of the study area

1.2 土壤样品采集与预处理

按照“S”型线路进行设点取样, 为保证样品代表性, 2020年10月于31个不同土地利用类型0~50 cm深度的样点, 每一采样点由上到下每10 cm取一份土样, 自然风干后研磨过100目孔筛。 SOC含量采用重铬酸钾容量法—外加热法测定, 单位为g·kg^-1。光谱数据采用美国ASD公司FieldSpec3型地物光谱仪测量。测量环境如下: 远离可能干扰土壤光谱的物体及环境, 选择云量小于5%、风力低于3级的晴朗天气, 时间为12:00—14:00; 视场角小于25°, 探头垂直于土样表面约15 cm处, 测量前对光谱仪进行预热与白板校正。采集光谱数据时采用五点梅花法, 每个土样共获得15条光谱曲线, 去除异常光谱值后, 对剩余曲线均值化得到最终的土样光谱数据。所有光谱曲线统一去除水汽影响较大的波段(1 300~1 450和1 800~1 950 nm)以及噪音影响较大的尾部波段(2 451~2 500 nm)^[8]。

1.3 土壤有机碳光谱估算模型开发

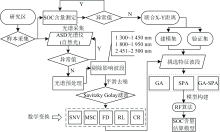
图2描述了SOC含量估算模型的构建流程: (1)对采集的土壤样品测定SOC含量与光谱反射率数据; (2)采用Savitzky Golay(SG)滤波方法对光谱曲线进行平滑和去噪, 并对原始光谱反射率(reflectivity, R)分别进行标准正态变量变换(standard normal variable, SNV)、多元散射校正(multiple scatter correction, MSC)、一阶微分(first derivative, FD)、对数的倒数(reciprocal of logarithm, RL)与连续统去除(continnum removal, CR)5种光谱数学变换; (3)基于联合X-Y距离(sample set partitioning based on joint X-Y distances, SPXY)方法划分103个样本为训练集, 52个为验证集, 并采用GA、 SPA与GA-SPA算法对原始光谱R及5种变换光谱分别进行降维处理; (4)基于RF方法构建研究区SOC含量估算模型, 决定系数R²(coefficient of determination, R²)、均方根误差(root mean square error, RMSE)和相对分析误差(ratio of standard deviation to RMSE, RPD)评价模型的精度与稳定性, 当R²取值趋于1, RMSE越接近0, RPD≥2.00时, 表明模型的拟合度越高。

	Figure Option View Download New Window
	图2 SOC含量估算模型构建流程图Fig.2 Flow chart of constructing SOC content estimation model

1.4 降维处理方法

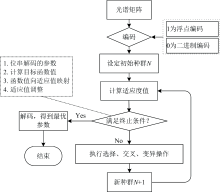
遗传算法(GA)是一种模拟学习生物界自然进化过程的算法, 旨在寻找最优种群, 能够减少谱矩阵的信息冗余和多重共线性问题, 降低陷入局部最优解的风险, 提高模型的精度。利用GA算法选择特征波段时, 种群数设置为60, 繁殖代数设置为100, 交叉概率设为0.6, 变异率设置为0.1, 采用北卡罗来纳大学gaot遗传算法工具箱。图3为GA算法过程图。

	Figure Option View Download New Window
	图3 GA算法挑选特征变量过程图Fig.3 Process diagram of selecting feature variables by GA algorithm

连续投影算法(SPA)是一种基于向前变量选择的方法, 并从光谱矩阵中选择共线性最小变量组合的算法。通过最小化矢量空间共线性, 采用向量投影分析挑选最大向量, 最后经过模型校正筛选光谱的特征波长, 减少了模型的冗余度, 提高了模型的稳定性和可靠性。算法中特征波长数的迭代范围设置为2~35, 通过建立多元线性回归模型交叉验证得到的一个均方根误差值RMSE, 选择其中最小的RMSE值对应的波长和波长数确定为最后的最优值。

(3)GA-SPA算法。为进一步简化模型, 在GA算法基础上应用SPA算法继续进行特征波段的筛选, GA算法在选择特征变量的过程中具有很强的随机性, SPA算法倾向于在选择特征波长的过程中选择具有较少共线性的波长, GA算法通过多重计算以最高精度选择变量, 结合SPA算法, 可以有效选择功能带。

1.5 模型构建方法

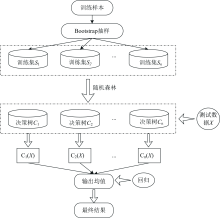
随机森林(RF)是一种采用随机森林分类器对新数据进行判别和分类的算法。在处理比较大的数据时, 运算速度快, 无需进行变量的选择; 在计算变量的非线性效应与处理连续和离散数据时, 它能够很好地容忍噪声和离群点的影响, 充分反映变量之间的相互作用^[9]。在算法模型建立过程中, 设置决策树的数量为500。图4为RF方法过程图。

	Figure Option View Download New Window
	图4 SOC含量RF模型构建过程图Fig.4 Construction process of RF model for soil organic carbon content

2 结果与讨论

2.1 光谱特征波段的挑选

2.1.1 基于GA算法挑选光谱特征波段

经GA算法处理后, 原始光谱R最终选择出407个波段作为特征变量, 占全波段的18.93%, 由图5可知, 原始光谱基于GA算法挑选的特征变量主要集中在350~410、 827~928、 997~1 064、 1 201~1 234、 1 541~1 574、 1 667~1 710、 2 153~2 186和2 357~2 707 nm。经SNV、 MSC、 FD、 RL和CR 光谱数据变换后, 光谱维数分别降低到697维、 668维、 667维、 493维、 784维, 分别占全光谱波段的32.42%, 31.07%, 31.02%、 22.93%、 36.47%。

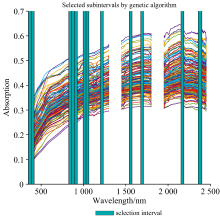	Figure Option View Download New Window
	图5 基于遗传算法挑选原始光谱特征波段的结果Fig.5 Results of selecting characteristic bands from original spectra based on Genetic Algorithm

2.1.2 基于SPA算法挑选光谱特征波段

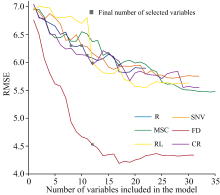
由图6可知, 基于SPA算法对原始光谱数据R进行特征波段筛选时, 当RMSE为6.09, 模型趋于稳定状态, 共挑选11个特征变量。光谱数据进行数学变换后挑选情况为: SNV、 MSC、 FD变换后光谱分别挑选了14个特征波段, RMSE值分别表现为6.00、 6.04、 4.86; RL变化光谱, 当RMSE为6.04时, 模型趋于稳定状态, 共挑选10个特征变量; CR变化光谱中, 当RMSE为6.39时, 共挑选了8个特征波段。

	Figure Option View Download New Window
	图6 利用SPA筛选光谱特征波长Fig.6 Screening of spectral characteristic wavelength by SPA

2.1.3 基于GA-SPA算法挑选光谱特征波段

由图7可知, 在原始光谱数据R中, 当RMSE为6.30时, 模型趋于稳定状态, 挑选了8个特征波段, 分别为407、 1 260、 1 700、 2 132、 2 153、 2 157、 2 186和2 360 nm; SNV光谱中, 当RMSE为6.30时, 得到了10个特征波段; MSC光谱中RMSE达到5.95时, 共挑选了17个特征波段; FD与RL光谱分别挑选了12个特征波段, RMSE值分别表现为4.53、 5.99; CR光谱中, 当RMSE为6.27时模型较稳定, 选择了11个特征波段。

	Figure Option View Download New Window
	图7 利用GA-SPA筛选光谱特征波长Fig.7 Screening of spectral characteristic wavelength by GA-SPA

2.2 构建土壤有机碳含量的高光谱估算模型

由表1可知, 原始光谱R中, 采用GA算法挑选的特征波段构建的RF模型 $R_{c}^{2}$ 为0.66, $R_{p}^{2}$ 为0.52, RPD为1.48。光谱经数学变换后, 建模效果最好的为FD、 RL光谱, $R_{c}^{2}$ 分别为0.71; 其次为MSC、 SNV光谱形式, CR效果最差, $R_{c}^{2}$ 只有0.62; 从模型的预测效果来看, 预测效果最好的为FD模型, RPD为1.64, $R_{p}^{2}$ 为0.74, RMSE_p为4.98, CR模型预测结果最差, RPD只有1.24。

表1 基于GA算法挑选特征波段构建RF模型 Table 1 Selecting characteristic bands based on GA algorithm to construct RF model

Transformation form	Train set		Validation set
Transformation form	$R_{c}^{2}$	RMSE_c	$R_{p}^{2}$	RMSE_p	RPD
R	0.66	5.56	0.52	5.74	1.48
SNV	0.68	5.73	0.53	5.28	1.43
MSC	0.70	4.83	0.51	5.30	1.57
FD	0.71	5.21	0.74	4.98	1.64
RL	0.71	5.70	0.63	5.70	1.61
CR	0.62	5.67	0.54	5.55	1.24

表1 基于GA算法挑选特征波段构建RF模型 Table 1 Selecting characteristic bands based on GA algorithm to construct RF model

由表2可知, 通过SPA算法挑选光谱数据的特征波段时, 光谱数据经数学变换后, 效果明显好于原始波段, 原始波段R建模效果最差, $R_{c}^{2}$ 仅有0.51; 基于FD光谱构建的模型效果最好, 建模集 $R_{c}^{2}$ 为0.79, RMSE_c为4.57; 其次为CR光谱, 建模集 $R_{c}^{2}$ 为0.76, RMSE_c为3.30。从预测结果来看, FD与CR光谱构建的模型验证效果最好, $R_{p}^{2}$ 分别为0.77、 0.66, 但是CR光谱的更稳定, 拟合度相对更高, RPD为1.92; RL光谱验证效果最差, $R_{p}^{2}$ 为0.52, RPD为1.60。

表2 基于SPA算法挑选特征波段构建RF模型 Table 2 Selecting characteristic bands based on GA algorithm to construct RF model

Transformation form	Train set		Validation set
Transformation form	$R_{c}^{2}$	RMSE_c	$R_{p}^{2}$	RMSE_p	RPD
R	0.51	5.84	0.62	6.24	1.63
SNV	0.68	5.23	0.63	6.39	1.65
MSC	0.70	5.16	0.59	6.72	1.64
FD	0.79	4.57	0.77	6.90	1.85
RL	0.72	6.05	0.52	6.54	1.60
CR	0.76	3.30	0.66	5.05	1.92

表2 基于SPA算法挑选特征波段构建RF模型 Table 2 Selecting characteristic bands based on GA algorithm to construct RF model

由表3可知, 在GA算法的基础上结合SPA算法构建的RF模型效果明显有所提升。建模效果最好的光谱转换为SNV, $R_{c}^{2}$ 为0.85, RMSE_c为6.30, 其次为FD、 R、 CR与RL转换, $R_{c}^{2}$ 均大于0.70, MSC转换光谱建模效果最差, $R_{c}^{2}$ 仅有0.65。模型的预测集 $R_{p}^{2}$ 均大于0.70, 效果最好的是SNV、 FD与RL转换光谱, $R_{p}^{2}$ 分别为0.82、 0.82、 0.80, 原始光谱R预测效果最差, $R_{p}^{2}$ 为0.71。综合来看, 光谱建模效果SNV光谱好于FD 光谱, 两者的预测集 $R_{p}^{2}$ 均为0.82, 但是SNV光谱RMSE_p与RPD均低于FD光谱, FD光谱的预测集RMSE_p为4.50, RPD为2.18。

表3 基于GA-SPA算法挑选特征波段构建RF模型 Table 3 Based on GA-SPA algorithm to select characteristic bands to construct RF model

Transformation form	Train set		Validation set
Transformation form	$R_{c}^{2}$	RMSE_c	$R_{p}^{2}$	RMSE_p	RPD
R	0.73	7.66	0.71	7.66	1.17
SNV	0.85	6.30	0.82	6.69	1.90
MSC	0.65	6.49	0.78	5.88	1.97
FD	0.78	5.48	0.82	4.50	2.18
RL	0.71	6.87	0.80	5.83	2.09
CR	0.73	7.26	0.72	5.72	2.00

表3 基于GA-SPA算法挑选特征波段构建RF模型 Table 3 Based on GA-SPA algorithm to select characteristic bands to construct RF model

基于GA、 SPA、 GA-SPA算法构建的RF模型中, 光谱反射率经过FD形式变换后, 模型的预测效果一直较好且稳定, $R_{p}^{2}$ 分别为0.74、 0.77、 0.82, 这表明一阶微分在光谱的信息增强中, 能够很好地分离重叠样品、减弱噪音和基线的影响, 这与张俊华等^[10]、勾宇轩等^[11]的研究结果基本一致。原始光谱与五种变换光谱通过SPA算法筛选出VIS-NIR光谱中与SOC含量相关性高的响应波段, 所构建的RF模型建模集的 $R_{c}^{2}$ 最高为0.79, 均高于GA算法构建的估算模型, 这与汪六三等^[12]研究结果基本一致, 表明SPA算法对于挑选SOC含量的特征波段是一种有效的方法。从模型的稳定性角度来说, 无论是单一的SPA算法还是GA算法挑选的特征波段, 其构建的SOC含量RF模型的RPD值均小于2.00, 这可能是由于VIS-NIR波谱范围较宽, 受到水汽、天气等因素的干扰, 增加了波谱信息的冗余程度, 同时可能因为土壤有机碳的组成成分较复杂, 加大了估算模型的复杂程度, 影响了模型预测能力。单一算法应用方面, VIS-NIR光谱数据中SPA算法优于GA算法建模, 具有更好的选择特征波长能力。 GA算法处理光谱数据时能够考虑到全局, 无论是面对离散还是连续数据都能够有效地进行全局式的搜索, 但是面对局部搜索时, 处理能力较差, SPA算法恰好能够弥补这一缺点, 消除繁杂的冗余光谱。由以上结果可知, 基于GA-SPA算法构建的RF模型, 验证集 $R_{p}^{2}$ 均高于单一的SPA与GA算法构建的模型, 这与刘燕德等^[13]研究结果基本一致, 多种算法融合能够以较少的特征波长数得到明显高于单方法的建模效果。章海亮等^[14]在原始光谱中, 基于GA-SPA算法共挑选了18个特征波段, 其构建的偏最小二乘模型 $R_{p}^{2}$ 为0.83, RMSE_p为4.50, RPD为2.45; 研究中基于GA-SPA算法共挑选了8个特征波段, 构建的RF模型 $R_{p}^{2}$ 为0.82, RMSE_p为4.50, RPD为2.18, 因此, GA-SPA算法结合RF方法建立的模型更有稳定性。 SOC的分布因受母质、地形、天气、成土年龄等不同环境因素的影响, 具有较强的变异性, 难以用固有的模型去估算不同区域的SOC含量。因此, 该模型的迁移性与普适性有待于进一步研究。

3 结论

(1)在原始光谱R中, 基于GA算法筛选SOC含量的高光谱响应波段主要集中在350~410、 827~928、 997~1064、 1 201~1 234、 1 541~1 574、 1 667~1 710、 2 153~2 186和2 357~2 707 nm。 GA算法筛选波段时原始光谱R及SNV、 MSC、 FD、 RL和CR光谱的维数分别降低到407、 697、 668、 667、 493、 784维, 占全光谱波段的18.93%~36.47%。

(2)基于SPA算法挑选特征波段, 当模型趋于稳定状态时筛选的特征变量只有8~14个, RMSE介于6.00~6.39。 GA-SPA算法筛选后, 模型的特征变量介于8~17个, RMSE介于4.53~6.30。

(3)基于GA-SPA算法构建的RF模型, 验证集 $R_{p}^{2}$ 均高于单一的SPA与GA算法构建的模型。光谱数据经FD数学变换后, 模型预测效果最好, 基于GA-SPA算法筛选的特征波段所构建的RF模型能够较好的估算SOC含量, 模型的建模集 $R_{c}^{2}$ 为0.78, 验证集 $R_{p}^{2}$ 为0.82, RMSE_p为4.50, RPD为2.18。

参考文献

文献列表

[1]	Bojko O, Kabala C. Catena, 2017, 149: 209. [本文引用:1]
[2]	LI Guan-wen, GAO Xiao-hong, XIAO Neng-wen, et al(李冠稳, 高小红, 肖能文, 等). Acta Optica Sinica(光学学报), 2019, 39(9): 361. [本文引用:1]
[3]	ZHOU Mi, XIAO Hai-bing, NIE Xiao-dong, et al(周咪, 肖海兵, 聂小东, 等). Research of Soil and Water Conservation(水土保持研究), 2020, 27(3): 391. [本文引用:1]
[4]	ZOU Hui-min, LI Xi-can, SHANG Xuan, et al(邹慧敏, 李西灿, 尚璇, 等). Science of Surveying and Mapping(测绘科学), 2019, 44(5): 146. [本文引用:1]
[5]	Moura-Bueno J M, Dalmolin R S D, Caten A T, et al. Geoderma, 2019, 337: 565. [本文引用:1]
[6]	Wang B, Waters C, Orgill S, et al. Ecological Indicators, 2018, 88: 425. [本文引用:1]
[7]	XIAO Yan, XIN Hong-bo, WANG Bin, et al(肖艳, 辛洪波, 王斌, 等). Remote Sensing for Land & Resources(国土资源遥感), 2021, 33(2): 33. [本文引用:1]
[8]	ZHANG Zi-peng, DING Jian-li, WANG Jing-zhe(张子鹏, 丁建丽, 王敬哲). Acta Optica Sinica(光学学报), 2019, 39(2): 391. [本文引用:1]
[9]	ZHANG Juan-juan, XI Lei, YANG Xiang-yang, et al(张娟娟, 席磊, 杨向阳, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2020, 36(17): 135. [本文引用:1]
[10]	ZHANG Jun-hua, JIA Ping-ping, SUN Yuan, et al(张俊华, 贾萍萍, 孙媛, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2019, 35(12): 106. [本文引用:1]
[11]	GOU Yu-xuan, ZHAO Yun-ze, LI Yong, et al(勾宇轩, 赵云泽, 李勇, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2022, 53(3): 331. [本文引用:1]
[12]	WANG Liu-san, LU Cui-ping, WANG Ru-jing, et al(汪六三, 鲁翠萍, 王儒敬, 等). Chinese Journal of Luminescence(发光学报), 2018, 39(7): 1016. [本文引用:1]
[13]	LIU Yan-de, XIAO Huai-chun, SUN Xu-dong, et al(刘燕德, 肖怀春, 孙旭东, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2018, 34(3): 180. [本文引用:1]
[14]	ZHANG Hai-liang, LUO Wei, LIU Xue-mei, et al(章海亮, 罗微, 刘雪梅, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(2): 584. [本文引用:1]

2017

0.0

... 具有重大作用与意义^[1] ...

2019

0.0

... 随着高光谱遥感技术的发展, 土壤反射光谱成为一种快速、高效的土壤属性估算方法, 学者们关于光谱信息的预处理^[2]、特征变量选择^[3]、建模手段^[4]等方面做了大量的研究 ...

2020

0.0

2019

0.0

2019

0.0

... Moura-Bueno等采用导数、归一化和非线性变换等六种预处理技术与偏最小二乘、多元线性回归、支持向量机和随机森林算法(random forest, RF)四种多元校正方法以确定预测SOC含量的最佳组合^[5] ...

2018

0.0

... 48^[6] ...

2021

0.0

... 12^[7] ...

2019

0.0

... 所有光谱曲线统一去除水汽影响较大的波段(1 300~1 450和1 800~1 950 nm)以及噪音影响较大的尾部波段(2 451~2 500 nm)^[8] ...

2020

0.0

... 在计算变量的非线性效应与处理连续和离散数据时, 它能够很好地容忍噪声和离群点的影响, 充分反映变量之间的相互作用^[9] ...

2019

0.0

... 82, 这表明一阶微分在光谱的信息增强中, 能够很好地分离重叠样品、减弱噪音和基线的影响, 这与张俊华等^[10]、勾宇轩等^[11]的研究结果基本一致 ...

2022

0.0

... 82, 这表明一阶微分在光谱的信息增强中, 能够很好地分离重叠样品、减弱噪音和基线的影响, 这与张俊华等^[10]、勾宇轩等^[11]的研究结果基本一致 ...

2018

0.0

... 79, 均高于GA算法构建的估算模型, 这与汪六三等^[12]研究结果基本一致, 表明SPA算法对于挑选SOC含量的特征波段是一种有效的方法 ...

2018

0.0

... 由以上结果可知, 基于GA-SPA算法构建的RF模型, 验证集 Rp2均高于单一的SPA与GA算法构建的模型, 这与刘燕德等^[13]研究结果基本一致, 多种算法融合能够以较少的特征波长数得到明显高于单方法的建模效果 ...

2017

0.0

... 章海亮等^[14]在原始光谱中, 基于GA-SPA算法共挑选了18个特征波段, 其构建的偏最小二乘模型 Rp2为0 ...