RF-iPLS算法的有效性验证试验采用的近红外光谱数据集为谷物蛋白质CGL_NIR, 数据来源http://eigenvector.com/resources/data-sets/。 该光谱数据集包含231个谷物样本, 117个光谱波长, 样本光谱波长范围1 104~2 495 nm。 将231个谷物样本随机划分为70%建模集和30%预测集, 建模集包含161个样本, 预测集包含70个样本。 以谷物蛋白质的含量作为因变量进行近红外光谱数据波长选择建模预测分析。 使用Python语言调用scikit-learn工具包搭建RF及PLS的回归模型。

RF通过抽样放回(Bootstrap)的方法从原始样本集N个样本中有放回地随机抽取n个样本, 原始样本集的2/3样本组成决策树的训练集, 剩余1/3未抽取的样本构成OOB, 用于计算特征重要性^[14]。 由于RF的双重随机性, 仅使用特征属性在RF决策树中的出现频率来体现特征重要性并不可取, 因此, 为了更准确地反映特征的重要性, 选择基于OOB数据的平均精度下降(mean decrease accuracy, MDA)方法计算均方误差平均值作为特征的重要性。 假设RF中有T棵决策树, 则基于OOB数据的MDA方法计算特征变量重要性过程如下:

(1)对于每棵决策树t_m(m=1, …, T), 输入OOB数据的矩阵X_OOB, 预测结果为Y_p, 预测值Y_p与真实值Y的均方误差ε _OOBm=mse(Y_p-Y)²。

(2)OOB数据的其他特征变量保持不变, 只打乱X_OOB中的第i列特征变量顺序重新排列, 即 XiOOB, 利用决策树t_m对打乱顺序重新排列后的样本进行预测, 预测结果为 Ypi, 预测值 Ypi与真实值Y的均方误差 εiOOBm=mse( Ypi-Y)²。

(3)特征变量 XiOOB对决策树t_m预测的均方误差结果为$\text{ms}{{\text{e}}^{i}}_{\text{OOB}m}\text{=}{{\varepsilon }^{i}}_{\text{OOB}m}-{{\varepsilon }_{OOBm}}$。

(4)重复(1)— (3), 遍历整个随机森林模型, 得到特征变量 XiOOB对所有决策树的均方误差$\text{ms}{{\text{e}}^{i}}_{\text{OOB}1}$ , $\text{ms}{{\text{e}}^{i}}_{\text{OOB}2}$ , …, $\text{ms}{{\text{e}}^{i}}_{\text{OOB}T}$ , 那么特征变量 XiOOB的重要性结果为

IMPi(XOOBi)=1T∑t=1TmseOOBmi(1)

通过RF特征重要性进行特征波长的初选, 得到的波长对于因变量变化最为敏感; 同时, 因模型输入的变量存在随机性, 筛选出的特征波长还存在一定的冗余, 难以保证特征波长筛选的有效性。 iPLS选择的特征波段区间建立的PLS模型效果较好, 但选择的波长较多且不能选取离散特征波长, 连续特征波段中依然存在信息冗余^[15]。 RF特征重要性筛选的离散特征波长解决了iPLS筛选的连续波段中含冗余信息的问题, 而iPLS通过对特征波长子集划分区间, 弥补了RF因自身随机性造成的无效变量问题。 因此, 提出RF-iPLS相结合的二次特征波长筛选方法, 对RF筛选出的特征子集进行改进, 结合iPLS方法, 将特征子集划分为n个子区间, 比较各个区间PLS模型的RMSEC的值, 将最小的RMSEC对应区间的波长作为最优特征波长子集, 消除特征波长的随机性, 避免无信息变量及干扰噪声。

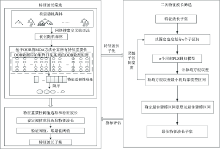
RF-iPLS算法流程如图1所示。 RF-iPLS算法主要为根据RF特征重要性筛选特征波长子集以及利用iPLS算法消除特征波长的随机性并得到最优特征子集的过程。 RF-iPLS算法的具体方法和步骤如下:

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 RF-iPLS算法流程图Fig.1 Flow diagram of the RF-iPLS

(1)建立初始RF模型, 然后使用网络搜索交叉验证方法优化RF模型, 利用式(1)对全光谱进行特征重要性计算并降序排序;

(2)设置特征重要性阈值, 若特征变量重要性大于此阈值, 则提取这部分变量, 并将特征变量按照特征重要性结果从大到小依次排列, 构成特征波长子集;

(3)将特征波长子集通过iPLS进行二次波长筛选, 调整子区间宽度, 将离散特征波长组合成局部连续特征波段, 建立局部PLSR回归模型, 以寻找RMSEC最小为目标进行iPLS二次优选特征波长。

近红外定量分析模型中, 模型评价包括建模集和预测集样本对模型的评价, 常用的评价指标包括建模集均方误差RMSEC和决定系数 Rc2, 预测集均方误差RMSEP、 决定系数 Rp2和分析相对误差(ratio of prediction to deviation, RPD)^[16]。 其中, R²值越接近1, RMSEC和RMSEP越接近0, RPD值越大, 表示预测值与参考化学值之间误差越小, 定量分析模型的预测能力越强, 精度越高。

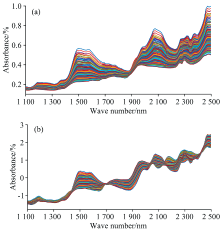
图2为231个谷物样本在1 104~2 495 nm范围内的近红外光谱图。 由图2(a)可见, 谷物蛋白质近红外光谱存在明显的基线漂移和噪声干扰引起的不平滑等问题。 为了在全光谱区域内校正光谱基线、 消除相关噪声的干扰, 减少光谱数据在一定程度上的线性相关, 利用SNV方法对原始光谱数据进行预处理, 预处理后的近红外光谱图如图2(b)所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 谷物样本近红外光谱图 (a): 原始近红外光谱图; (b): 预处理后的近红外光谱图Fig.2 Near infrared spectra of grain samples (a): Original near infrared spectra; (b): Preprocessed near infrared spectra

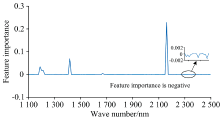
根据上述RF的MDA方法, 对117个全光谱波长计算特征重要性并排序, 图3为RF特征重要性结果与近红外光谱之间的关系, 当光谱特征变量和因变量存在强相关性时, 特征重要性结果为正值^[7]。 当某变量的特征重要性值越大时, 说明该变量在RF模型中与因变量存在强相关性^{[17, 18]}, 那么优选该变量为特征变量。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 特征重要性与近红外光谱的关系Fig.3 Relationship between feature importance and near infrared spectra

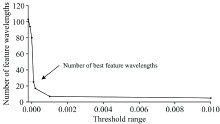
从图3可知, 多个变量的特征重要性结果为零和负值, 表明这些变量与因变量之间存在无关性和弱相关性。 因此, 特征重要性阈值选取的范围为{-0.000 2, -0.000 1, 0.000 0, 0.000 1, 0.000 2, 0.001, 0.01}, 阈值与特征波长筛选的数学关系如图4所示, 可以看出阈值与特征波长个数之间呈现反比例关系, 即特征重要性阈值越接近零, 特征波长个数越多。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 阈值与特征波长筛选的关系Fig.4 Relationship between threshold and feature wavelength selection

对上述不同阈值范围内筛选出的特征波长建立PLSR预测模型, 比较不同阈值范围内的特征波长预测结果。 如表1所示, 随着特征重要性阈值不断增大, 特征波长数和运行时间不断减小, RMSEP的结果变化整体趋势为先减小后增大, Rp2的结果呈现先增大后减小的趋势。 经过对比可知, 当阈值取值范围在-0.000 2~0.000 0之间时, RMSEP变化范围在2.47~2.51之间, Rp2变化范围是0.984~0.985, 说明此时筛选的波长子集中包含了一定的无效信息或干扰变量^[19], 这都将影响模型的精度和效率。 根据表1, 当阈值为0.000 1时, 特征波长数从117减少到25, 模型运行时间从5.373 s缩短到1.591 s; 预测集RMSEP和 Rp2分别为1.94和0.993, 此时25个特征波长构成的特征波长子集对谷物蛋白质含量预测模型具有极佳的分析性能; 因此特征波长数取25时构成的特征子集, 使RF-PLSR模型达到最佳性能。 此时, 特征波长子集的波长范围是1 104~2 472 nm。

表1

Table 1

表1(Table 1)

表1 不同阈值范围内的特征波长预测结果 Table 1 Prediction results of characteristic wavelength in different threshold ranges 阈值大小(≥ ) 特征波长数 RMSEP Rp2 账行时间/s -0.000 2 103 2.47 0.984 5.373 -0.000 1 94 2.51 0.984 4.955 0.000 0 80 2.47 0.985 4.533 0.000 1 25 1.94 0.993 1.591 0.000 2 17 2.05 0.992 1.243 0.001 7 2.16 0.988 1.197 0.01 5 2.33 0.986 1.024

表1 不同阈值范围内的特征波长预测结果 Table 1 Prediction results of characteristic wavelength in different threshold ranges

将经过RF特征重要性筛选出的25个特征波长, 按照特征重要性值的大小对其进行提取并排序, 得到特征波长子集。 采用iPLS算法对该特征波长子集完成二次特征波长筛选, 消除特征子集中因随机性产生的无效波长变量或干扰变量, 筛选出关键特征波长进行建模。 将得到的特征波长子集进行区间划分, 区间数量n从1依次增加到5, 并基于这些区间的特征变量分别构建PLSR模型, 以RMSEC最小为原则筛选最佳的建模区间。 图5为不同区间个数时, iPLS模型的最佳建模区间评估参数的变化趋势。 随着n逐渐增大, RMSEC和RMSEP值呈现先减小后逐渐增加, Rc2和RPD的值均先增加后减小, 显示出了RF特征重要性筛选的特征波长子集中含有一定的波长冗余。 结合表2可知, 当区间数为1时, PLSR模型性能最差, 说明特征子集中含有无效或干扰变量^[20]; 当区间数为2时, 特征波长数从25减少到12, 建模集的RMSEC为0.64, Rc2的值从0.984增加至0.998, 预测集的RMSEP为0.69, Rp2从0.993增加至0.997; 且该区间内有最小的RMSEC和最大的 Rc2, 分别为0.64和0.998。 根据以上结果分析可知, 当iPLS子区间数量为2时所对应的特征波段为最优特征波段, 此时该区间为第1区间且该区间内特征波长数为12个, 分别为2 160、 1 416、 1 188、 1 212、 1 200、 1 668、 1 680、 1 308、 2 412、 2 388、 1 224和2 172 nm。

图5

Fig.5

	Figure Option ViewDownloadNew Window
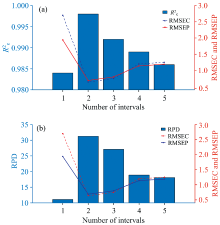	图5 不同区间个数时模型评估参数的变化趋势 (a): RMSE与R2; (b): RMSE与RPDFig.5 Variation trend of model evaluation parameters at different interval numbers (a): RMSE and R2; (b): RMSE and RPD

表2

Table 2

表2(Table 2)

表2 不同区间个数的RF-iPLS优选结果 Table 2 Optimization results of RF-iPLS model with different interval numbers 区间 个数 特征 波长数 建模集 预测集 RPD RMSEC Rc2 RMSEP Rp2 1 25 2.70 0.984 1.94 0.993 11.09 2 12 0.64 0.998 0.69 0.997 31.26 3 8 0.75 0.992 0.80 0.993 27.09 4 6 1.20 0.989 1.14 0.991 18.89 5 5 1.25 0.986 1.19 0.991 18.09

表2 不同区间个数的RF-iPLS优选结果 Table 2 Optimization results of RF-iPLS model with different interval numbers

根据表2结果可知, iPLS在挑选特征波段的过程中, 区间个数的选择在很大程度上影响RF-iPLS, 且随着区间个数的增加, RF-iPLS模型的计算量随之增大; 同样, iPLS波长筛选时也会受到区间个数的影响, 有时甚至会选入大量的无关信息^[21], 导致预测模型效果不佳。 因此, 对RF-iPLS算法, 选择合适的区间个数, 对特征波长信息的筛选及建立良好预测性能的模型至关重要。

2.4.1 波长筛选结果分析

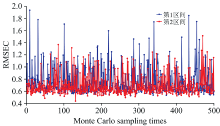
为了说明RF-iPLS算法区间划分的合理性, 将特征波长子集经过MC的500次特征波长样本随机采样后, 如前所述, 按照区间个数为2时进行二次波长筛选。 如图6所示, MC采样次数为131时, RMSEC在第2区间中有最小值, 最小值为0.44, 此时筛选的波长变量数为13个。 13个波长变量分别是2 160、 1 188、 1 212、 1 200、 1 680、 1 308、 2 388、 1 224、 2 364、 2 256、 1 692、 1 248和2 472 nm。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 MC样本采样500次后的RMSEC变化趋势Fig.6 RMSEC variation trend of MC samples after 500 sampling times

将谷物蛋白近红外光谱数据运用RF-iPLS和RF-MC-iPLS算法, 分别获取到12个和13个特征波长, 构建基于PLSR的预测模型。 结果对比如表3所示, 经过MC对特征波长子集进行波长随机采样后, RF-MC-iPLS的模型中建模集的RMSEC和 Rc2以及预测集的 Rp2略有提升, 预测效果略优于 RF-iPLS, 但是RF-iPLS比RF-MC-iPLS算法的模型运行时间缩短了约11.12倍。 从波长数量来看, RF-iPLS与RF-MC-iPLS算法的特征波长分别为12和13, 波长数量约为全谱的1/9, RF-iPLS与RF-MC-iPLS算法均能够减少波长冗余信息, 提高预测精度, 使模型更简单; 从运行时间来看, RF-iPLS模型具有快速、 高效率的优势; 从预测精度来看, RF-MC-iPLS模型在不考虑牺牲运行时间的情况下, 预测精度略高。 总体来看, RF-iPLS算法能够有效的筛选出该样本中与谷物蛋白质相关的特征波长信息。

表3

Table 3

表3(Table 3)

表3 RF-iPLS与RF-MC-iPLS结果分析 Table 3 Results analysis of RF-iPLS and RF-MC-iPLS 波长筛选方法 特征 波长数 建模集 预测集 运行 时间/s RMSEC Rc2 RMSEP Rp2 RF-iPLS 12 0.64 0.998 0.69 0.997 8.03 RF-MC-iPLS 13 0.44 0.999 0.69 0.998 89.30

表3 RF-iPLS与RF-MC-iPLS结果分析 Table 3 Results analysis of RF-iPLS and RF-MC-iPLS

RF-iPLS与RF-MC-iPLS算法筛选的波长结果对比可知, 二者相同的波长为2 160、 1 188、 1 212、 1 200、 1 680、 1 308、 2 388和1 224 nm, 主要分布在1 110~1 680 nm区域内, 该区域包含蛋白质的氨基N— H键、 水O— H键和醇O— H键的伸缩振动的一级倍频, 碳链C— H键(— CH, — CH₂和— CH₃基团)的第二组合频和二级倍频等结构光谱信息, 表明这8个特征波长可能与样品中的蛋白质浓度有较高的相关性; 同时, RF-iPLS与RF-MC-iPLS算法筛选波长的结果存在差异, RF-iPLS算法筛选出1 416、 1 668、 2 412和2 172 nm, RF-MC-iPLS算法筛选出2 364、 2 256、 1 692、 1 248和2 472 nm, 范围在1 248~1 692和2 172~2 472 nm之间, 其中在2 172~2 472 nm区域内, 对应着蛋白质的碳链C— H键的组合频和一级倍频、 C=O的伸缩振动一级倍频以及N— H伸缩振动与AmideⅡ 的合频, 基本涵盖RF-iPLS算法筛选的上述4条波长; RF-MC-iPLS比RF-iPLS算法筛选的特征波长多1条且预测结果略优于RF-iPLS模型, 原因可能是该区域中某些波长与样品中的谷物蛋白质浓度特别相关。 总体来看, 通过设置MC对特征波长子集进行随机采样, 验证了RF-iPLS算法能够筛选出有效波长, 提高模型预测能力; 同时, RF-iPLS算法筛选出的波段与图7(b)近红外光谱曲线吸收峰的位置基本一致, 符合Ridgway等^[22]的论点, 即光谱曲线上的凸起区可能对蛋白质含量预测有实际意义。

图7

Fig.7

	Figure Option ViewDownloadNew Window
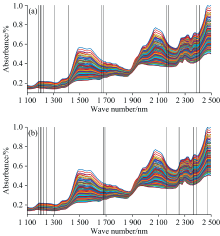	图7 特征波长分布图 (a): RF-iPLS; (b): RF-MC-iPLSFig.7 Feature wavelength distribution (a): RF-iPLS; (b): RF-MC-iPLS

2.4.2 定量分析的结果比较

为验证RF-iPLS模型的性能, 分别将全光谱和GA, SPA, RF和iPLS方法筛选的特征波长作为PLSR模型的输入。 各个波长筛选算法的特征波长数量和预测结果如表4所示, 全光谱模型的特征波长数最多, 模型运行时间最长, 预测效果最差。 相较于全光谱模型FULL-PLSR, 5种特征波长筛选算法都有效地提高模型的预测能力, 结合模型预测结果、 建立模型的波长数和谷物蛋白真实值与预测值拟合关系来看, 显然, 在近红外光谱分析过程中, 特征波长筛选是可行的、 有必要的。

表4

Table 4

表4(Table 4)

表4 不同波长筛选的预测结果比较 Table 4 Comparison of prediction results of different wavelength selection 波长筛选 方法 特征 波长数 建模集 预测集 RPD RMSEC Rc2 RMSEP Rp2 Full 117 2.61 0.987 2.63 0.982 8.72 GA 51 2.53 0.987 2.55 0.983 9.02 SPA 28 2.41 0.989 2.34 0.986 9.81 RF 25 2.71 0.984 1.94 0.993 11.09 iPLS 58 0.29 0.975 0.52 0.987 41.40 RF-iPLS 12 0.64 0.998 0.69 0.997 31.96

表4 不同波长筛选的预测结果比较 Table 4 Comparison of prediction results of different wavelength selection

模型预测结果如表4所示, 在波长筛选方法对比中, 虽然GA和SPA的建模集效果RMSEC和 Rc2均优于RF, 但RF-PLSR模型的预测集RMSEP, Rp2和RPD均优于二者, 说明其模型预测能力好于GA-PLSR和SPA-PLSR; 从特征波长数量方面来看, GA筛选出51个特征波长, 约为RF-PLSR模型的2倍; SPA筛选的特征波长数为28个, RF筛选的特征波长数有25个, 显然以上三种波长筛选方法中, RF筛选出的特征波长数最少, 表明RF特征重要性筛选出的特征波长能够消除噪声, 提高预测能力。 构建iPLS预测模型时, 区间个数设为2时, RMSEC值最小。 虽然模型的RMSEC和RMSEP均是最小值, 但 Rc2和 Rp2低于其他特征波长筛选后的模型, 且该模型的波长数约为RF-iPLS模型的4.8倍; RF模型的预测集各项参数和RPD均优于全谱、 GA及SPA模型, RF-iPLS算法模型的各项参数均优于RF。 基于RF所选的特征波长的PLSR模型的 Rp2为0.993, RMSEP为1.94, RPD为11.09, 特征波长数为25; RF-iPLS算法进行二次波长筛选后建立的预测模型中, Rp2和RMSEP分别为0.997和0.69, RPD为31.96, 特征波长数约为RF筛选的特征波长子集的1/2。 因此, 经过RF-iPLS算法二次波长筛选后, 其模型的预测精度有了明显的提升。 综上所述, RF-iPLS算法可以筛选出有效的波长信息, 减少波长冗余, 提高预测的精度。

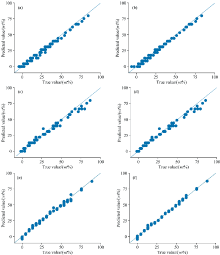
全光谱、 GA、 SPA、 RF、 iPLS和RF-iPLS方法筛选的特征波长建立谷物蛋白质预测模型, 模型的真实值与预测值的散点拟合图如图8所示。 从图8(f)中可以更直观地看出, 六个模型中RF-iPLS模型的预测效果最好, 数据点集中在拟合直线的两侧, 而其他模型的数据点分布较分散, 由此可见, 近红外光谱结合RF-iPLS算法筛选特征波长并建立预测模型, 具有很高的预测准确度, 可以实现谷物中蛋白质含量的定量分析。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 谷物蛋白质含量真实值与预测值的关系图 (a): Full; (b): GA; (c): SPA; (d): RF; (e): iPLS; (f): RF-iPLSFig.8 Relationship between true value and predicted value of grain protein content (a): Full; (b): GA; (c): SPA; (d): RF; (e): iPLS; (f): RF-iPLS