一种CEEMDAN联合双树复小波的水质紫外-可见光谱去噪算法研究

引用本文

汪仁杰, 冯鹏, 杨兴, 安乐, 黄盼, 罗燕, 何鹏, 汤斌. 一种CEEMDAN联合双树复小波的水质紫外-可见光谱去噪算法研究[J]. 光谱学与光谱分析, 2023,43(3): 976-983.
WANG Ren-jie, FENG Peng, YANG Xing, AN Le, HUANG Pan, LUO Yan, HE Peng, TANG Bin. A Denoising Algorithm for Ultraviolet-Visible Spectrum Based on CEEMDAN and Dual-Tree Complex Wavelet Transform[J]. Spectroscopy and Spectral Analysis, 2023,43(3): 976-983.
Doi:10.3964/j.issn.1000-0593(2023)03-0976-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

一种CEEMDAN联合双树复小波的水质紫外-可见光谱去噪算法研究

汪仁杰^1,², 冯鹏^1,^*, 杨兴³, 安乐³, 黄盼¹, 罗燕¹, 何鹏¹, 汤斌^1,^2,^*

1.重庆大学光电技术及系统教育部重点实验室, 重庆 400044

2.重庆市光纤传感与光电检测重点实验室, 重庆 400054

3.成都理工大学计算机与网络安全学院, 四川成都 610059

*通讯作者 e-mail: coe-fp@cqu.edu.cn; tangbin@cqut.edu.cn

作者简介: 汪仁杰, 1996年生, 重庆理工大学现代光电检测技术与仪器重点实验室硕士研究生 e-mail: 821721959@qq.com

收稿日期: 2021-11-19 修回日期: 2022-05-25 接受日期: 2022-05-25

基金: 国家自然科学基金青年科学基金项目(61805029), 重庆市研究生科研创新项目(CYS22109), 重庆市自然科学基金项目(cstc2020jcyj-msxmX0553)资助

摘要

紫外-可见吸收光谱法测量水质化学需氧量(COD), 本质是对大量水质光谱数据建模, 以此模型为基础引入待测的水质光谱数据进行预测的过程。而实测的邻苯二甲酸氢钾COD标准溶液在200~300 nm存在两个特征吸收峰, 标准溶液在不同浓度下的峰值也不同, 利用此特性对该波段进行特征波长的选择, 用其表征光谱信息, 降低数据冗余度的同时提高了预测精度。针对实测水质光谱信号容易受到仪器本身和外界干扰, 光谱数据存在大量非平稳噪声, 且特征吸收峰及其临近信号频率较高, 常规去噪算法直接舍弃高频信号以及无法准确判断信噪分量界限, 导致有效信号缺失这一实际问题。提出了一种基于完全自适应噪声集合经验模态分解(CEEMDAN)和双树复小波变换(DT-CWT)的联合去噪算法。该联合算法利用CEEMDAN将信号分解为本征模态函数(IMF), 并通过归一化自相关函数和互相关系数进行线性相关性分析, 得到各阶IMF分量之间的自相关性以及IMF分量与原始信号的互相关系数, 以确定高频含噪分量与低频信号分量的界限; 进而应用DT-CWT阈值去噪算法对含噪高频IMF分量进行处理, 将DT-CWT处理之后的IMF高频分量与CEEMDAN分解得到的IMF低频分量进行信号重构, 获得最终去噪后的水质光谱信号。实验结果表明: 基于CEEMDAN联合双树复小波变换的去噪算法适用于紫外-可见光谱水质检测的数据处理。对于化学需氧量COD标液为100 mg·L^-1的邻苯二甲酸氢钾溶液, 将实测的紫外-可见光谱数据应用该算法去噪后的SNR=24.201 5 dB, RMSE=0.024 0, NCC=0.999 4, PSNR=37.573 6, 不仅去噪效果显著优于CEEMDAN和双树复小波阈值算法, 还有效地保留了原始COD标液的吸收特征峰, 遏制了平移敏感性现象, 提高了重构信号的平滑度, 改善了重构信号质量。为紫外-可见光谱法检测水质COD提供了一种新的数据预处理方法。

关键词: 水质检测; 紫外-可见光谱; 完全自适应噪声集合经验模态分解(CEEMDAN); 双树复小波变换; 相关分析

中图分类号:X593 文献标志码:A

A Denoising Algorithm for Ultraviolet-Visible Spectrum Based on CEEMDAN and Dual-Tree Complex Wavelet Transform

WANG Ren-jie^1,², FENG Peng^1,^*, YANG Xing³, AN Le³, HUANG Pan¹, LUO Yan¹, HE Peng¹, TANG Bin^1,^2,^*

1. Key Laboratory of Optoelectronic Technology and Systems of Ministry of Education, Chongqing University, Chongqing 400044, China

2. Chongqing Key Laboratory of Optical Fiber Sensing and Photoelectric Detection, Chongqing University of Technology, Chongqing 400054, China

3. College of Computer and Cyber Security, Chengdu University of Technology, Chengdu 610059, China

*Corresponding authors

Abstract

The essence of measuring water quality COD by UV-vis absorption spectrometry is to model a large number of spectral data, and then introduce the measured spectral data to predict the process. However, there are two characteristic absorption peaks in the measured COD standard solution of potassium hydrogen phthalate at 200~300 nm, and the peak and peak values of the standard solution are also different at different concentrations. This feature is used to select the characteristic wavelength of this band and use it to characterize the spectral information, which reduces the data redundancy and improves the prediction accuracy. Because the measured water quality spectral signal is easily disturbed by the internal and external interference, resulting in a large number of non-stationary noise in the spectral data, and the characteristic absorption peak and its adjacent signal frequency is high, conventional denoising algorithms directly abandon high-frequency signals and can not accurately judge the limits of signal-to-noise components, resulting in the lack of effective signals. A joint denoising algorithm based on fully adaptive noise set empirical mode decomposition CEEMDAN (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise) and dual-tree complex wavelet transform DT-CWT (The Dual-Tree Complex Wavelet Transform) is proposed. The algorithm uses CEEMDAN to decompose the signal into intrinsic mode function IMF (Intrinsic Mode Function). It makes linear correlation analysis through normalized autocorrelation function and cross-correlation number to determine the boundary between high-frequency noise components and low-frequency signal components. Then the DT-CWT threshold denoising algorithm is used to process the noisy high-frequency IMF component, and the IMF high-frequency component after DT-CWT processing is reconstructed from the IMF low-frequency component demarcated by CEEMDAN, and the final denoised signal is obtained. The experimental results show that the denoising algorithm based on CEEMDAN combined with dual-tree complex wavelet transform is suitable for data processing of UV-Vis spectrum water quality detection. For potassium hydrogen phthalate solution whose chemical oxygen demand (COD) standard solution is 100 mg·L^-1, the denoising effect of SNR=24.201 5 dB, RMSE=0.024 0, NCC=0.999 4 and PSNR=37.573 6 denoised by the combined algorithm is significantly better than that of CEEMDAN and double-tree complex wavelet threshold algorithm. Moreover, it effectively retains the characteristic absorption peak of the original COD standard solution, suppresses the translation sensitivity and improves the smoothness of the reconstructed signal. The quality of the reconstructed signal is improved. It provides a new data pre-processing method for detecting water quality COD by UV-Vis spectrum.

Keyword: Water quality measurement; UV-Vis spectrum; CEEMDAN; DT-CWT; Correlation analysis

文章图片

引言

随着我国工业化和城镇化规模的的不断扩大, 水环境污染问题愈发严重。因此对水体环境/水质进行检测和监测, 实现实时预警, 已尤为迫切^[1]。目前, 化学需氧量(chemical oxygen demand, COD)是用以评估水体有机污染程度应用最为广泛的指标, 其被定义为由强氧化剂(如重铬酸盐、高锰酸盐)氧化水体中还原性物质所消耗的氧的当量^[2]。 COD数值与污水的有机物污染程度成正比, 数值越大, 对水环境的破坏越严重。国标法规定检测COD的方法主要为重铬酸钾氧化法和高锰酸盐指数法, 虽然检测精度较高, 但化学方法存在操作复杂、测量周期长、产出废液等缺点^[3]。近年来, 采用紫外-可见光谱法进行水质COD检测已成为研究热点, 这是一种无需化学试剂、无二次污染的绿色无损检测技术, 受到国内外广泛关注^[4]。

实测水质光谱信号会受到来自于光源、光路、光电转换器件、外界干扰等多个方面的噪声影响^[5], 严重影响光谱信号特征峰的定位与识别, 降低水质预测模型的准确性和适应性。近年来, 不少国内外学者在拉曼光谱、近红外光谱去噪领域有着广泛深入的研究。李卿等采用经验模态分解(empirical mode decomposition, EMD)方法, 不失真分解和重构拉曼光谱信号, 相比传统小波变换, 具有自适应性, 无需人为选定小波基、阈值和分解层数, 但易引起模态混叠和端点效应等问题^[6]; Wang等提出了总体经验模态分解(ensemble empirical mode decomposition, EEMD)的方法, 缓解了EMD模态混叠的问题^[7], 但增加了计算时间; Tang等提出了互补集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD), 进一步减弱模态混叠效应且提高了计算效率^[8]; Anindya等也对EEMD进行了改进, 提出了完全自适应噪声集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN), 具有更好的模态频谱分离和更高的计算效率, 同时也克服了EEMD的虚假分量缺陷; Chen等为了消除可见光与红外光谱噪声, 提出了基于改进双树复小波(dual-tree complex wavelet transform, DT-CWT)的光谱去噪算法, 相比传统小波具有近似平移不变性和抑制模态混叠的优点^[9], 但该方法仅能去除高频噪声, 无法去除混杂在低频的细节噪声。

对于水质预测模型, 紫外-可见光谱数据200~300 nm波段的两处特征吸收峰可以表征90%以上的光谱信息, 其核心就在于对其特征峰进行建模。然而特征吸收尖峰及其邻近信号频率极高, 常规去噪方法难以有效划分信噪分量分离点, 因此导致COD解算的偏离。本研究提出了一种CEEMDAN联合DT-CWT的去噪方法。 CEEMDAN具有很好的模态分离特性和信号完备性, 可以将实测信号分解为频率从高到低的一系列本征模态函数, 噪声分量在其前N阶高频分量当中; 但是前N阶同样含有少量的有用信号, 因此引入双树复小波, 对前N阶高频分量再次进行信号提取, 在消除或减弱光谱噪声的同时, 利用DT-CWT的平移不变性以保证谱峰位置检测的准确性, 进一步提升水质光谱数据的信噪比。

1 算法原理

1.1 CEEMDAN理论及去噪算法

CEEMDAN以集合经验模态分解(EEMD)为基础, 将EEMD分解得到的每一阶本征模态函数分量(intrinsic mode function, IMF)添加自适应白噪声, 并计算唯一的残差信号以获取固有模态函数。定义符号IMF_k为集合平均得到的模态分量, E_j(g)表示通过EMD产生的第j个模态分量, ω _i(t)为满足N(0, 1)分布的高斯白噪声信号, 设待处理光谱信号为x(t), 包含以下步骤:

①对原始信号x(t)添加不同的高斯白噪声ω _i(t), 则原始信号变成x_i(t)=x(t)+ε ₀ω _i(t), ε ₀表示噪声标准差, 用EMD方法对集合中每一个合成信号x_i(t)进行I次分解, 对其进行集合平均获得一阶IMF分量, 见式(1)

$IM F_{1} (t) = \frac{1}{I} \overset{I}{\sum_{i = 1}} IM F_{i 1} (t)$ (1)

去除原始信号中的模态分量IMF₁, 得到第一个残差信号r₁(t), 表示为式(2)

$r_{1} (t) = x (t) - IM F_{1} (t)$ (2)

②对信号r₁(t)+ε ₁E₁(ω _i(t))进行I次分解, 获得二阶IMF分量, 见式(3)

$IM F_{2} (t) = \frac{1}{I} \overset{I}{\sum_{i = 1}} E_{1} {(r}_{1} (t) + ε_{1} E_{1} {(ω}_{i} (t)))$ (3)

对于k=2, …, K, 计算K阶残差分量, 见式(4)

$r_{k} (t) = r_{k - 1} (t) - IM F_{k} (t)$ (4)

③提取信号r_k(t)+ε _kE_k(ω _i(t))的K阶IMF分量, 求出k+1阶模态分量, 见式(5)

$IM F_{k + 1} (t) = \frac{1}{I} \overset{I}{\sum_{i = 1}} E_{k} {(r}_{k} (t) + ε_{k} E_{k} {(ω}_{i} (t)))$ (5)

④重复步骤②, 直至残差信号分量为单调函数, 不能再分解为止, 最终可得到K个本征模态函数, 最后的残差信号, 见式(6)

$R (t) = x (t) - \overset{K}{\sum_{k = 1}} IM F_{k} (t)$ (6)

即原始信号x(t)可以表示为式(7)

$x (t) = R (t) + \overset{K}{\sum_{k = 1}} IM F_{k} (t)$ (7)

从CEEMDAN方法的原理看出, CEEMDAN可以将光谱信号模态分解成频率从高到低的一系列IMF分量, 相比EEMD具有更好的模态频谱分离能力, 进一步改善模态混叠效应和避免虚假IMF分量。其中随机噪声主要分布在前几阶高频分量中, 然而仍旧没有明确的方法来确定CEEMDAN信噪分量分界点。在去噪研究中, 常用来判定信号分量与噪声分量的方法有排列熵、 Shannon熵等^[10], 本研究将对CEEMDAN分解后的各阶IMF分量与原始信号进行相关性分析来确定。相关性原理判定与计算熵值相比, 不仅噪声层级精确, 而且更具简易性, 相关系数公式见式(8)

$ρ (i) = \frac{\overset{L}{\sum_{j = 1}} x (j) IM F_{i} (j)}{\sqrt[]{\overset{L}{\sum_{j = 1}} x^{2} (j) \overset{L}{\sum_{j = 1}} IM F_{i}^{2} (j)}}$ (8)

式(8)中: L为信号长度, ρ (i)代表第i阶IMF分量与原始信号x(t)之间的相关系数。计算得到各阶IMF分量的相关系数后, 绘制出相关系数的关系图。信号的高频噪声分量阶数与相关系数存在一定的规律: 当含噪信号x(t)信噪比非常大时, 设分解的IMF分量为M阶, 第1~N阶处相关系数均较小, 从N+1阶起相关系数会突然增大, 且N+1~M阶总体呈上升趋势, 此时可以认为1~N阶为噪声分量。最后直接舍弃掉前N阶高频IMF分量, 将N+1~M阶IMF分量重构, 得到去噪后的信号。

1.2 双树复小波变换(DT-CWT)理论及去噪算法

针对实小波变换不具有平移不变性和频率混叠的缺陷, Kingsbbury在1998年提出双树复小波变换(DT-CWT)。相较于实小波变换, 特有的抗频率混叠和平移不变性等特点, 在信号滤波降噪等方面优于许多时频分析方法。 DT-CWT是两路并行的实小波变换结构, 即实树和虚树, 进而实现对信号的分解以及重构。在信号分解与重构时, 使实树采样点比虚树采样点相隔一个采样周期, 让虚树的采样点在实树之间, 正好采集到实树因隔点采样丢失的采样值, 达到充分利用双树的小波分解系数的目的, 实现信号平移不变性, 减少有用信号的丢失。

基于双树复小波变换(DT-CWT)去噪算法: 含有大量非平稳噪声的紫外-可见光谱信号经过双树复小波变换后, 有效信号分量大多数包含在小波系数的低频部分, 含噪信号分量基本在高频部分。在信号分解过程中, 设定一个合适的阈值, 将低于该阈值的小波系数全部置零, 将高于设定阈值的小波系数保留, 最后进行小波逆变换得到重构后的信号。

阈值的选取方法主要有硬阈值法和软阈值法两种, 由于软阈值的去噪方法在连续性和去噪效果上优于硬阈值方法, 因此采用软阈值的处理方法。

软阈值表达式

$f (x) = \{\begin{array}{l} sgn (x) (| x | - γ), & | x | \geq γ \\ 0, & | x | < γ \end{array}$ (9)

式(9)中, γ 为全局阈值, 其表达式为式(10)

$γ = σ \times \sqrt[]{2 \lg N}$ (10)

f(x)为阈值处理后的小波系数, x为小波系数, N为信号长度, σ 为噪声标准差。

信号经过软阈值法处理后, 能够最大程度地保留信号有用成分, 达到去噪目的。

基本步骤是:

①将原始信号进行双树复小波变换, 设定分解层数, 对信号进行分解, 得到一组系数;

②应用软阈值法选取合适的阈值, 确定信噪分量的界限, 对每层含噪高频系数进行阈值处理;

③对信号进行重构: 将阈值处理后的高频系数与未处理的低频系数进行重构, 得到最终的去噪信号。

2 CEEMDAN联合DT-CWT的光谱去噪算法

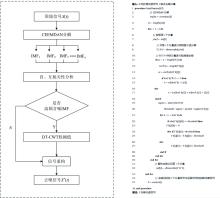
对于实测水质紫外-可见吸收光谱, 位于200~300 nm之间第一和第二特征吸收峰包含了吸收光谱的绝大部分信息, 但吸收尖峰及其临近频率极高, 传统的去噪方法难以做到信噪分离的同时保证吸收峰的信号完整性。 CEEMDAN方法相比EEMD具有良好的抗模态混叠和克服虚假分量的特点, 且计算效率大大提高, 当含噪光谱信号中包含较小幅度的有效信息时, 采用CEEMDAN分解原始信号得到的本征模态函数, 采用相关性分析分离出高频含噪分量和低频信号分量, 若直接舍弃高频含噪分量去噪会造成高频噪声压制不完全或高频有效信号损失。双树复小波变换相比传统小波, 具有良好的平移不变性和抗频率混叠的特性, 处理后的信号波形较为平滑, 且使得水质光谱信号去噪前后不会出现基线漂移等现象。鉴于此, 提出了将CEEMDAN和DT-CWT联合的方法, 通过互补的方式解决上述去噪过程中的问题。针对CEEMDAN分解出的前N阶高频IMF分量中可能含有较小幅度的有用信号, 采用DT-CWT对前N阶高频IMF分量进行再去噪, 最终将DT-CWT处理后的高频IMF分量与CEEMDAN分解的未处理IMF分量重构得到去噪后的光谱。该联合算法保证了光谱吸收特征峰在横纵向同时满足良好的完备性, 进而保证水质预测模型的准确性。同时, 因CEEMDAN算法和DT-CWT算法均具有较少的冗余性和良好的鲁棒性, 使计算效率大大提高, 更适用于水质在线监测^[10]。算法流程和伪代码图如图1。

	Figure Option View Download New Window
	图1 联合算法去噪流程及伪代码图Fig.1 Denoising flow and pseudo code diagram of joint algorithm

联合去噪算法的基本流程分为三个步骤:

①对原始信号进行CEEMDAN分解, 得到各阶IMF分量; 对IMF分量进行相关性分析, 根据相关系数大小确定含噪IMF分量和信号IMF分量的界限;

②由于前几阶高频分量中仍含有少量细节信号, 将确定为噪声分量的前几阶IMF分量分别进行DT-CWT软阈值提取细节信号, 然后小波逆变换得到重构后的IMF分量;

③将步骤②中处理之后得到的重构IMF分量与①中未处理IMF分量再次进行重构, 得到最后的去噪信号。

3 结果与讨论

3.1 实验设置

紫外-可见吸收光谱法的水质检测系统如图2所示。为了验证所提出算法的理论可行性, 分别采用(1)海洋光学(型号: Maya2000Pro)光谱仪和(2)超微光学(型号: OTO HB2030)光谱仪: (1)为标准光谱对照组, 测量波段200~1 100 nm, 测量2 068个点; (2)为原始光谱实验组, 测量波段180~850 nm, 测量1 581个点。为了排除多余的可控变量, 实验除光谱仪型号不同外, 其余实验条件均保持一致: 采用氘卤灯组合式光源(型号: Sarspec LS-DWHP)作为光谱发生器, 波长范围为200~1 100 nm; 相同的光路结构(支架型号: Ocean optics ACH* CUV-VAR), 光程为8 cm; 石英比色皿(型号: 光亮高科751-10), 容量3.5 mL, 光程10 mm; 采用抗紫外光纤(型号: Ocean optics P600-1-UV-VIS), 长度为1 m; 本实验所用样本溶液为一组邻苯二甲酸氢钾COD标液, 浓度为100 mg· L^-1。

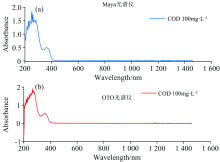
	Figure Option View Download New Window
	图2 紫外-可见光谱法水质检测系统框图Fig.2 Block diagram of water quality detection system with UV-Vis spectrometry

将上述仪器设备按照图2搭建实验系统, 两组光谱仪分别对样本溶液进行50次测量, 光谱仪采集软件设置积分时间20 ms。紫外-可见光谱波段在200~780 nm, 因此截取两组光谱仪200~780 nm区间的光谱数据为有效数据区间。图3(a)为海洋光学Maya2000pro光谱仪所测一组吸收光谱图, 图3(b)为超微光学OTO HB2030光谱仪所测吸收光谱图。

	Figure Option View Download New Window
	图3 Maya原始信号(a)和OTO原始信号(b)Fig.3 Maya raw signal (a) and OTO raw signal (b)

对于两组光谱仪对照实验, 实测COD标液的吸收光谱在200~300 nm之间出现两个特征吸收峰, 如图3(a, b)。

为了仔细观察两个吸收特征峰的波形, 将两组光谱仪在200~300 nm的光谱信息放大, 如图4(a, b)。

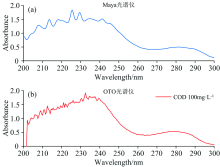	Figure Option View Download New Window
	图4 Maya原始信号(a)和OTO原始信号(b)200~300 nm对比Fig.4 Maya raw signal (a) and OTO raw signal (b) 200~300 nm comparison

可以明显观察到OTO HB2030的吸收光谱的第一特征峰出现较多毛刺和尖峰, Maya 2000pro的曲线较为平滑且在特征峰位置无较多干扰信息, 两组光谱仪的第二特征吸收峰波形均平滑且高信噪比。

以Maya 2000pro的测量结果作为标准光谱信号, 将实测的OTO HB2030吸收光谱数据分别用CEEDMAN分解、 DT-CWT阈值及本研究算法去噪处理。为了定性定量地分析实验结果, 引入去噪效果评价指标: 信噪比(signal to Noise Ratio, SNR)、均方根误差(root mean square error, RMSE)、波形相似度(normalied correlation coefficient, NCC)和峰值信噪比(peak signal to noise ratio, PSNR)。去噪后的SNR越大, 说明去噪效果越好; RMSE表示原始信号与去噪后信号之间的方差平方根, 越小测量精度越高; NCC反映的是OTO去噪光谱与Maya标准光谱的波形差异, 差异越小, 证明去噪效果越好; 则PSNR指三种去噪算法结果与Maya的标准光谱作对比, PSNR越大, 表明去噪之后的特征峰信息保留更多, 去噪效果越好。

信噪比见式(11)

$SNR = 10 \lg \frac{\overset{N}{\sum_{t = 1}} x^{2} (t)}{\overset{N}{\sum_{t = 1}} [x {(t) - \overset{*}{x (t)}]}^{2}}$ (11)

波形相似度见式(12)

$NCC = \frac{\overset{N}{\sum_{t = 1}} x (t) \overset{*}{x (t)}}{\sqrt[]{\overset{N}{\sum_{t = 1}} x^{2} (t) \overset{N}{\sum_{t = 1}} \overset{*}{x {(t)}^{2}}}}$ (12)

均方根误差见式(13)

$RMSE = \sqrt[]{\frac{1}{N} \overset{N}{\sum_{t = 1}} [x {(t) - \overset{*}{x (t)}]}^{2}}$ (13)

峰值信噪比见式(14)

$PSNR = 10 \lg \frac{x^{2} {(t)}_{\max} \times N}{\overset{N}{\sum_{t = 1}} [x (t) - x {(\overset{*}{t})]}^{2}}$ (14)

式(11)— 式(14)中, x(t)为原始光谱信号, $\overset{*}{x (t)}$ 是去噪后的光谱信号, 其中t=1, …, N, N为信号长度。 x(t)_max表示信号x(t)的最大值。

3.2 相关系数计算

通常噪声频率高于信号频率, 随机噪声主要分布在阶次较低的高频分量内, 信号主要位于阶次较高的IMF分量中, 确定噪声与信号在IMF各阶分量占比的临界阈值尤为重要。根据信号和噪声相关性质的不同, 通过各阶IMF分量的自相关函数以及原始信号与各阶IMF分量之间的相关性来确定临界阈值。通过CEEMDAN分解得到频率从高到低的一系列IMF分量, 如图5。

	Figure Option View Download New Window
	图5 CEEMDAN分解的IMF分量Fig.5 IMF components of CEEMDAN decomposition

相关函数R_x(τ )表示信号x(t)在τ 时刻的自相关值, 表征信号在不同时刻的相似程度。 ρ _x(τ )则表示归一化的自相关系数

$R_{x} (τ) = \frac{1}{N} \overset{N - 1 - | τ |}{\sum_{t = 0}} x (t) x (t + τ)$ (15)

$ρ_{x} (τ) = \frac{R_{x} (τ)}{R_{x} (0)}$ (16)

式(15)和式(16)中, N为采样点的个数, τ 表示时间差。

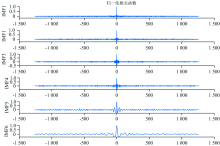
对于背景噪声, 具有不确定性以及在不同时刻的弱相关性, 其自相关函数曲线变化陡峭; 而对于有效信号, 其信号序列存在着一般变化规律以及明显的强相关性, 因此有效信号的自相关函数曲线波动缓慢。实验发现, 虽然两者都是在零点处取得最大值, 但是背景噪声自相关函数的衰减速度显著大于有效信号的衰减速度。图6罗列了前6项IMF分量的自相关函数。

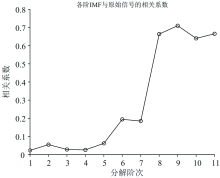
	Figure Option View Download New Window
	图6 前6阶IMF归一化自相关函数Fig.6 IMF normalized autocorrelation function of the first 6 orders

由图6各自相关函数曲线可以看出, 1~5阶IMF分量虽然在零点处取得了最大值, 但是在临近频率存在迅速衰减到很小的值的现象, 可以初步判定前5阶IMF分量为噪声分量。然而依据自相关函数波形来判断信噪分量分界点, 存在一定的主观性。因此再次求得各阶IMF分量与原始信号的互相关系数来佐证上述结论, 如图7所示。

	Figure Option View Download New Window
	图7 各阶IMF与原始信号的相关系数Fig.7 Correlation coefficient between each order IMF and the original signal

由图7可以看出, 1~5阶IMF分量与原始信号的相关性较低, 均小于0.03。 5~12阶总体呈上升趋势, 且均大于0.1。当相关系数小于0.1时, 可以判断该IMF分量为噪声主导序列, 所以判定1~5阶为噪声分量。

3.3 实验结果

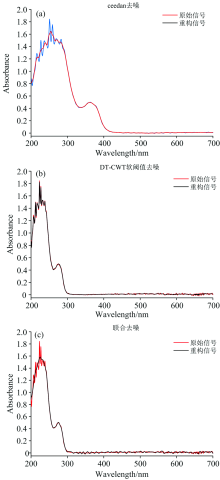
联合算法和单一去噪算法去噪的实验结果如图8(a, b, c)所示。

	Figure Option View Download New Window
	图8 三种去噪算法去噪前后对比 (a): Ceedan去噪; (b): DT-CWT软阈值去噪; (c): 联合去噪Fig.8 Comparison of three denoising algorithms before and after denoising (a): Denoising with ceedan; (b): Denoising with DT-CWT (soft thresholding); (c): Denoising with proposed method

由图8(a)不难看出, CEEMDAN的去噪效果较差, 可以观察到邻苯二甲酸氢钾溶液的第一特征峰还存在高频噪声, 波峰中心包含一个窄带尖峰, 失真比较严重; 第二特征峰经去噪后仅有轻微失真, 导致曲线不够平滑, 没有最大程度还原特征峰的有效信息; 对于DT-CWT阈值去噪[见图8(b)], 在处理特征峰时, 均达到了较好的效果。但原始信号的第二特征峰信噪比极高, 几乎没有噪声, 但实际去噪效果却反而降低了其峰值信噪比。分析认为软阈值处理时将第二特征峰的部分有效信息当作高频噪声滤除[见图8(c)]; 基于CEEMDAN和DT-CWT软阈值的去噪算法最佳, 第一、二特征峰均不存在失真现象, 较好地还原了COD标液的光谱吸收特征。

三种方法去噪后的信噪比、均方根误差等参数如表1所示。通过对比发现, 本算法在保留紫外-可见吸收光谱的吸收特征下, 提高了信噪比, 减小了均方根误差, 并具有最高的波形相似性。

表1 不同去噪效果的比较 Table 1 Comparison of denoising result with different methods

由去噪对比图8和表1中可以看出, 吸收光谱在三种方法处理之后的波形曲线均比较光滑, 噪声大大降低, CEEMDAN联合DT-CWT软阈值的去噪效果最好, 信噪比最高且均方根误差最小, 波形相似度与Maya标准光谱差异最小, 峰值信噪比达到最高。因三种方法的去噪效果均较好, 各个评价指标的数值差异不大, 为了防止偶然事件发生, 采用多次波形相似度测量取平均结果的论证方法, 图9是50次测量取平均的结果。

	Figure Option View Download New Window
	图9 NCC测量50组平均结果Fig.9 Average results of 50 groups of NCC measurements

结果表明, CEEMDAN去噪、 DT-CWT去噪、本算法去噪均获得了较好的去噪效果, 波形相似度均在0.98以上。相对而言, 本算法去噪的波形相似度最高, 去噪效果最好, 可有效抑制OTO光谱仪的随机噪声。

4 结论

去噪是水质光谱检测中必不可少的步骤。针对所采集光谱信号的非平稳性, 本文提出了CEEMDAN和DT-CWT联合的去噪算法, 并应用到水质检测系统中的紫外-可见光谱数据的预处理研究。该方法针对CEEMDAN分解之后的高频IMF分量中含有少量的信号分量, 采用自相关性和互相关系数来判别含噪高频IMF分量, 并对含噪高频IMF分量再次进行DT-CWT软阈值处理, 以获得更加细分、噪声更少的高频分量。理论分析和实测数据表明, 基于CEEMDAN和DT-CWT软阈值的去噪算法既能有效抑制光谱信号中的高频噪声, 提高了信噪比, 又能保持原始水质吸收光谱信号中的特征峰, 减少了均方根误差, 为水质检测系统的光谱数据去噪预处理提供了一种新的思路。

参考文献

文献列表

[1]	QI Wei, FENG Peng, WEI Biao(漆伟, 冯鹏, 魏彪). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(1): 194. [本文引用:1]
[2]	QI Meng-meng, HAN Yan-he, SUN Qi(齐蒙蒙, 韩严和, 孙齐). Environmental Science(环境科学), 2019, 38(11): 17. [本文引用:1]
[3]	Christian, Evelyn, Batista, et al. Water Environment Research, 2017, 89(2): 168. [本文引用:1]
[4]	ZHAO You-quan, WANG Hui-min, LIU Zi-yu(赵友全, 王慧敏, 刘子毓). Chinese Journal of Scientific Instrument(仪器仪表学报), 2010, 31(9): 1927. [本文引用:1]
[5]	Li Fengxiao, Tang Bin, Zhao Mingfu, et al. Journal of Spectroscopy, 2021, 2021: 6650630. [本文引用:1]
[6]	JIA Rong, LI Tao-tao, XIA Zhou(贾嵘, 李涛涛, 夏洲). Journal of Hydraulic Engineering(水利学报), 2017, 48(3): 334. [本文引用:1]
[7]	Wang W C, Chau K W, Xu D M, et al. Water Resources Management, 2015, 29(8): 2655. [本文引用:1]
[8]	Tang L, Dai W, Yu L, et al. International Journal of Information Technology & Decision Making, 2015, 14(1): 141. [本文引用:1]
[9]	Chen Xihui, Chen Gang, Li Hongyu, et al. Journal of Mechanical Science and Technology, 2017, 31(3): 1035. [本文引用:1]
[10]	LI Xiang-bo, GONG Jun, HU Dan(李相伯, 龚俊, 胡丹). Acta Photonica Sinica(光子学报), 2021, 50(5): 204. [本文引用:2]

2021

0.0

... 因此对水体环境/水质进行检测和监测, 实现实时预警, 已尤为迫切^[1] ...

2019

0.0

... 目前, 化学需氧量(chemical oxygen demand, COD)是用以评估水体有机污染程度应用最为广泛的指标, 其被定义为由强氧化剂(如重铬酸盐、高锰酸盐)氧化水体中还原性物质所消耗的氧的当量^[2] ...

2017

0.0

... 国标法规定检测COD的方法主要为重铬酸钾氧化法和高锰酸盐指数法, 虽然检测精度较高, 但化学方法存在操作复杂、测量周期长、产出废液等缺点^[3] ...

2010

0.0

... 近年来, 采用紫外-可见光谱法进行水质COD检测已成为研究热点, 这是一种无需化学试剂、无二次污染的绿色无损检测技术, 受到国内外广泛关注^[4] ...

2021

0.0

... 实测水质光谱信号会受到来自于光源、光路、光电转换器件、外界干扰等多个方面的噪声影响^[5], 严重影响光谱信号特征峰的定位与识别, 降低水质预测模型的准确性和适应性 ...

2017

0.0

... 李卿等采用经验模态分解(empirical mode decomposition, EMD)方法, 不失真分解和重构拉曼光谱信号, 相比传统小波变换, 具有自适应性, 无需人为选定小波基、阈值和分解层数, 但易引起模态混叠和端点效应等问题^[6] ...

2015

0.0

... Wang等提出了总体经验模态分解(ensemble empirical mode decomposition, EEMD)的方法, 缓解了EMD模态混叠的问题^[7], 但增加了计算时间 ...

2015

0.0

... Tang等提出了互补集合经验模态分解(complementary ensemble empirical mode decomposition, CEEMD), 进一步减弱模态混叠效应且提高了计算效率^[8] ...

2017

0.0

... Chen等为了消除可见光与红外光谱噪声, 提出了基于改进双树复小波(dual-tree complex wavelet transform, DT-CWT)的光谱去噪算法, 相比传统小波具有近似平移不变性和抑制模态混叠的优点^[9], 但该方法仅能去除高频噪声, 无法去除混杂在低频的细节噪声 ...

2021

0.0

... 在去噪研究中, 常用来判定信号分量与噪声分量的方法有排列熵、 Shannon熵等^[10], 本研究将对CEEMDAN分解后的各阶IMF分量与原始信号进行相关性分析来确定 ...

... 同时, 因CEEMDAN算法和DT-CWT算法均具有较少的冗余性和良好的鲁棒性, 使计算效率大大提高, 更适用于水质在线监测^[10] ...