基于多元极值优化的多光谱温度测量方法

引用本文

张璇, 曾朝斌, 刘娴雅, 陈平, 韩焱. 基于多元极值优化的多光谱温度测量方法[J]. 光谱学与光谱分析, 2023,43(3): 705-711.
ZHANG Xuan, ZENG Chao-bin, LIU Xian-ya, CHEN Ping, HAN Yan. Multi-Spectral Temperature Measurement Method Based on Multivariate Extreme Value Optimization[J]. Spectroscopy and Spectral Analysis, 2023,43(3): 705-711.
Doi:10.3964/j.issn.1000-0593(2023)03-0705-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于多元极值优化的多光谱温度测量方法

张璇¹, 曾朝斌¹, 刘娴雅¹, 陈平^1,^2,^3,^*, 韩焱^2,³

1.中北大学信息与通信工程学院, 山西太原 030051

2.山西省信息探测与处理重点实验室, 山西太原 030051

3.动态测试省部共建国家重点实验室, 山西太原 030051

*通讯作者 e-mail: pc0912@163.com

作者简介: 张璇, 1995年生, 中北大学信息与通信工程学院博士研究生 e-mail: 1094398770@qq.com

收稿日期: 2022-02-07 修回日期: 2022-05-11 接受日期: 2022-05-11

基金: 国家自然科学基金项目(61871351, 61971381, 61801437), 山西省研究生创新项目(2021Y609, 2021Y612)资助

摘要

多光谱测温依据黑体辐射定律, 通过辐射光强、多组波长即能推测出温度值, 克服了比色测温要求光谱单一和比色光谱相近的约束, 在工程实际中得到了广泛的应用。在多光谱温度反演的过程中, 光谱发射率的求解及多光谱数据处理是精确测温的关键。目前, 光谱发射率的求解大多以光谱发射率假设模型为主要的方法, 当假设模型与实际情况接近时, 反演的温度与光谱发射率精度很高, 当二者不相符时, 反演的结果与实际情况相差甚大, 对于复杂材料和燃烧过程中材料性能动态变化情况下的测温, 以光谱发射率假设模型的方法存在盲目性; 近年来, 基于神经网络的深度学习的方法应用于多光谱测温, 避免了光谱发射率假设模型, 可建立温度与多光谱的非线性统计规律关系, 但需要海量数据与超强算力支撑, 且建模过程复杂。针对上述问题, 提出了一种基于多元极值优化的多光谱温度测量方法(MEVO), 该方法利用不同温度下多光谱信号之间的关联性, 通过分析在多光谱温度反演过程中各通道测量温度之间的联系, 基于多光谱辐射测温原理以及温度反演过程中各通道数据之间的信息关联, 建立多元温差关联函数, 通过关联函数的寻优, 建立高精度测温模型。该方法将建模过程简化为多元温差函数的寻优问题, 避免了光谱发射率与其他物理量的关系假设, 降低了深度学习方法对数据样本量的要求, 简化了多光谱温度测量的过程。为了验证该方法的可行性与可靠性, 利用一套简单的8通道多谱测温装置进行实验验证, 实验中认定黑体炉发射的温度是标准值, 在1 923.15~2 273.15 K温区内对468~603 nm波段的光谱数据进行标定, 实现了基于多元极值优化的多光谱温度测量, 其测温精度在0.5%左右, 温度反演时间在2.5 s以内。与二次测量法(SMM)、神经网络方法相比反演精度有所提高; 反演速度与SMM法相比有大幅度提升。

关键词: 多光谱测温; 光谱发射率; 极值优化

中图分类号:O433.1 文献标志码:A

Multi-Spectral Temperature Measurement Method Based on Multivariate Extreme Value Optimization

ZHANG Xuan¹, ZENG Chao-bin¹, LIU Xian-ya¹, CHEN Ping^1,^2,^3,^*, HAN Yan^2,³

1. College of Information and Communication Engineering, North University of China, Taiyuan 030051, China

2. Shanxi Key Laboratory of Signal Capturing & Processing, Taiyuan 030051, China

3. State Key Laboratory of Dynamic Testing Technology, North University of China, Taiyuan 030051, China

Abstract

Multispectral thermometry is based on Blackbody radiationlaw, and the temperature value can be calculated based on the radiation intensity and multiple sets of wavelengths. This method has become widely used in engineering practice, as it overcomes the constraints of the single spectrum and similar colorimetric spectrum requirements for colorimetric temperature measurement. In multispectral temperature inversion, the solution of spectral emissivity and multispectral data processing are the keys to accurate temperature measurement. At present, the solution of spectral emissivity is mostly based on the assumption model of spectral emissivity. When the hypothetical model is close to reality, the accuracy of the inverted temperature and spectral emissivity is very high; otherwise, the inversion result deviates significantly. For the temperature measurement of complex materials and the dynamic changes of material properties during the combustion process, the method of assuming the model of spectral emissivity is groundless; In recent years, the deep learning method based on the neural network has been applied to multispectral temperature measurement, which avoids the assumption model of spectral emissivity, and can establish the nonlinear statistical relationship between temperature and multi spectrum, but it requires massive data and supercomputing power support, and the modeling process is complicated.In order to solve the above problems, this paper proposes a multispectral temperature measurement method named multi-element extreme value optimization (MEVO) measurement method. This method utilizes the correlation between multispectral signals at different temperatures, and by analyses the relationship between the measured temperatures of each channel in the process of multispectral temperature inversion, based on the principle of multispectral radiation temperature measurement and the information correlation between the data of each channel in the process of temperature inversion, establish a multivariate temperature difference correlation function, and establish a high-precision temperature measurement model through the optimization of the correlation function. This method simplifies the modeling process to the optimization problem of multivariate temperature difference function, avoids the assumption of the relationship between spectral emissivity and other physical quantities, reduces the requirement of data sample size for deep learning methods, and simplifies the process of multispectral temperature measurement. A simple 8-channel temperature measuring device was used for experimental verification. In the experiment, we determined that the temperature emitted by the Blackbody furnace was the standard value. The spectral data of the 468~603 nm band in the 1 923.15~2 273.15 K temperature zone was calibrated, and the multispectral thermometry based on the optimization of multiple extreme values was realized. The temperature measurement accuracy is about 0.5%, and the temperature inversion time is within 2.5 s. Compared with the second measurement method (SMM) and the neural network method, the inversion accuracy is substantially improved. Moreover, the inversion speed is significantly faster than the SMM method.

Keyword: Multispectral thermometry; Spectral emissivity; Extreme value optimization

文章图片

引言

非接触式辐射温度测量由于其不会与被测物体接触, 近些年来, 在诸多方面都有着广泛的应用^{[1, 2, 3, 4, 5]}。秦亚楼等人为研究激光毁伤中毁伤区域状态的变化, 基于激光毁伤目标区域的温度分布, 提出一种改进的多光谱测温方法对毁伤区域的辐射光谱进行反演分析; 通过对1 500 K温度下的目标辐射光谱的温度反演, 验证了所提方法的可行性^[6]; 张磊等基于多光谱测量理论, 设计了多通道光电探测器多光谱测温装置, 用钨标准化灯进行标定, 通过测量标准辐射源的温度验证了辐射测温方法的可行性^[7]; 邢键等人提出用外点罚函数约束优化算法处理多光谱测温数据, 分析了该算法与其他优化算法相比所具有的优势; 搭建了稻壳粉生物质锅炉炉膛火焰温度测量装置, 实验验证了测量装置及反演算法的可行性, 实现了生物质锅炉炉膛火焰燃烧温度的测量^[8]; Zhu等为了准确测量光谱发射率, 研究了309S钢样品表面氧化层生长过程中, 不同温度下光谱发射率与波长之间的解析关系, 分析对比了不同温度和不同加热时间下光谱发射率随波长的变化趋势, 建立了10种发射率模型, 利用所建立的模型在800~1 100 K温度范围内实现了不确定度在10 K以内的真温反演^[9]; Wang等通过分析光谱发射率随波长递变的变化趋势, 在约束优化算法的基础上提出了一种无需光谱发射率假设模型的测温方法, 该方法利用发射率与波长的曲线趋势来建立约束条件, 使用遗传算法作为优化工具, 在1 200~3 000 K温区内实现了相对误差小于1%的高精度温度测量^[10]; Suleiman等通过分析高强度钢(AHSS)在临界退火过程中光谱发射率的变化对高温测量的影响, 提出了一种模拟先进高强度钢光谱发射率的经验方法, 建立了一种先进高强度合金钢多变量光谱发射率模型, 用3通道的高温计对退火后样品的光谱发射率进行了拟合, 结果表明预测值与实测值能够较好的吻合^[11]; Liu等将光谱发射率和波长之间建立起多项式函数关系, 采用高光谱图像处理完成了乙烯火焰的测量, 采用牛顿迭代法求解, 实现了煤烟火焰温度和光谱发射率的反演^[12]; 赵玉清等对各种测温方法进行分析, 提出了采用多光谱测温法对爆炸过程中辐射功率的测量和光谱发射率的最佳拟合计算爆炸的真实温度, 设计了高爆弹药辐射温度及温场测试与校准设备, 利用所提测温方法在650~2 100 nm波段实现了高爆弹药辐射温度的反演^[13]; 张福才等利用多组光学探头通过光纤远传, 获取多光谱多通道的测量数据, 在无需预先假设发射率与波长之间的模型关系基础上, 通过迭代法获得表面某些点的真温, 并在2 000 K以上的温度场对所提方法进行了验证^[14]; 孙红胜等针对彩色CCD多波长成像测温的不足, 提出了一种基于光阑处非等比例滤色分光的4波长无扫描成像测温方法, 有效压缩了波段成像带宽, 并根据提出的测温方法研制了4波长成像测温仪, 在激光加热条件下对800~2 500 ℃目标高温温场进行了试验测试, 结果表明所提测温方法具有较高的准确度和较好的动态范围适应性^[15]; 席剑辉等提出了一种基于PCA-ELM的多光谱测温方法, 引入主元分析(principal component analysis, PCA)方法降低神经网络输入维数, 基于极限学习机(extreme learning machine, ELM)对样本数据充分学习, 建立PCA-ELM目标测温模型, 以黑体和未知发射率材料涂层目标为测试源, 验证了该方法的有效性^[16]。

综上所述, 在多光谱辐射测温过程中, 往往需要假定光谱发射率与其他物理量(波长或真温)之间的函数关系式才能实现真温的反演, 而且只有当光谱发射率假设模型与待测物体光谱发射率的实际情况接近时才能取得较好的反演结果, 不适用于所有材料的真温反演。然而, 在复杂结构材料燃烧温度测量中, 例如火炸药等特种能源材料, 其组成材料复杂, 一般均由多种不同配比的材料组成, 配比不同则辐射特性不同, 导致难以用静态材料的光谱发射率去描述其辐射特性; 此外在燃烧过程中, 材料的光谱发射率会动态变化, 即使能够在静态下测量其光谱发射率, 也与实际燃烧有很大的差异。针对复杂新型材料的温度测量的需求, 提出了一种基于多元极值优化的多光谱温度测量方法(multi-element extreme value optimization measurement method, MEVO), 避免了光谱发射率与其他物理量的关系假设, 简化了多光谱温度测量模型, 且反演精度较高、反演速度较快。

1 基于多元极值优化的真温反演原理

根据黑体辐射定律可知, 绝对温度为T的物体在波长λ 下的辐射亮度为

$L (λ, T) = C_{1} ε_{λ} (π λ^{5} e^{C_{2} / λT})^{- 1}$ (1)

式(1)中, L(λ , T)为物体的辐射亮度(W· m^-2· μ m^-1· sr^-1), λ 为波长(μ m), T为绝对温度(K); ε _λ为物体在温度T时的光谱发射率; C₁=3.741 5× 10⁸ W· μ m⁴· m^-2; C₂=1.438 79× 10⁴ μ m⁴· K。

由式(1)可知, 温度T的物体会在不同的波长λ _i下辐射出不同的能量L(λ _i, T), 假设探测器的输出电压信号为

$\begin{array}{l} V_{λ_{i}} = τ_{λ_{i}} S_{λ_{i}} L (λ_{i}, T) = τ_{λ_{i}} S_{λ_{i}} C_{1} ε_{λ_{i}} (π λ_{i}^{5} e^{C_{2} / λ_{i} T})^{- 1} \\ i = 1, 2, \dots, n \end{array}$ (2)

式(2)中, $τ_{λ_{i}}$ 和 $S_{λ_{i}}$ 分别表示只与波长有关而与温度无关的光学系统的透过率和光敏器件灵敏度的检定常数, λ _i是多波长测温计不同通道对应的波长, C₂是第二辐射常数, n是多波长测温计的通道数。

由比色测温的基本理论可知, 根据式(3), 选取探测器两个波长λ _i和λ _j处的电压信号作比值处理, 假设物体在相近波长处的光谱发射率 $ε_{λ_{i}}$ 和 $ε_{λ_{j}}$ 近似相等, 可得

$\frac{V_{λ_{i}}}{V_{λ_{j}}} = \frac{τ_{λ_{i}} S_{λ_{i}} L (λ_{i}, T)}{τ_{λ_{j}} S_{λ_{j}} L (λ_{j}, T)} = \frac{τ_{λ_{i}} S_{λ_{i}} λ_{j}^{5}}{τ_{λ_{j}} S_{λ_{j}} λ_{i}^{5}} \exp [\frac{C_{2}}{T} (\frac{1}{λ_{j}} - \frac{1}{λ_{i}})]$ (3)

式(3)中, $V_{λ_{i}}$ 和 $V_{λ_{j}}$ 表示探测器在相近两个波长处的电压值。根据比色测温的相关知识可知, 比色测温要求波长相近且光谱单一, 但在工程上光谱扩散导致实际测量中很难做到光谱单一的要求, 这也是比色测温引入误差的主要原因之一。为了避免这种情况, 选用基于参考温度的多光谱温度测量数学模型, 在同一波长处进行比值处理, 利用多通道光谱之间的交互耦合来弥补谱扩散带来的误差问题。

由式(2)可知, 当黑体炉产生某一标准温度T_rb时, 会在不同波长λ _i下辐射出不同的能量, 此时探测器的输出电压信号为

$V_{λ_{i} b} = A_{λ_{i}} ε_{λ_{i}} (π λ_{i}^{5} e^{C_{2} / λ_{i} T_{rb}})^{- 1}$ (4)

式(4)中, $A_{λ_{i}}$ 是与波长、光学系统透过率、光敏器件灵敏度和第一辐射常数有关的检定常数即 $A_{λ_{i}}$ = $τ_{λ_{i}} S_{λ_{i}}$ C₁。由于黑体炉产生的是标准辐射, 因此发射率近似为1即 $ε_{λ_{i}}$ =1, 式(4)可简化为

$V_{λ_{i} b} = A_{λ_{i}} (π λ_{i}^{5} e^{C_{2} / λ_{i} T_{rb}})^{- 1}$ (5)

依据基于参考温度的多光谱测温数学模型, 将式(2)和式(5)相除, 可得

$\frac{V_{λ_{i}}}{V_{λ_{i} b}} = ε_{λ_{i}} e^{C_{2} / λ_{i} T_{rb}} / e^{C_{2} / λ_{i} T}$ (6)

式(6)消除了与波长、光学系统透过率、光敏器件灵敏度和第一辐射常数有关的检定常数 $A_{λ_{i}}$ , 在多光谱真温反演过程中 $A_{λ_{i}}$ 的标定过程相对复杂且对精度的要求很高, 直接利用式(2)进行温度反演可能会引入较大的误差, 消除 $A_{λ_{i}}$ 避免了因系统标定不准带来的误差问题。

由式(6)可得多波长测温计i通道表示的测量温度 $T_{λ_{i}}$

$T_{λ_{i}} = \frac{1}{\frac{1}{T_{rb}} + \frac{λ_{i}}{C_{2}} \ln (\frac{ε_{λ_{i}} V_{λ_{i} b}}{V_{λ_{i}}})}$ (7)

1.1 多元温差函数

对于同一时刻待测物体的同一点, 其温度在理论上是唯一的, 即用式(7)表示的不同通道测量的温度 $T_{λ_{i}}$ 是相等的, 取相邻通道测量的温度差的平方和表示为

$(T_{λ_{1}} - T_{λ_{2}})^{2} + (T_{λ_{2}} - T_{λ_{3}})^{2} + \dots + (T_{λ_{n - 1}} - T_{λ_{n}})^{2} = 0$ (8)

当式(8)成立时, ( $T_{λ_{n}}$ - $T_{λ_{1}}$ )²=0也成立, 可得

$\begin{array}{l} (T_{λ_{1}} - T_{λ_{2}})^{2} + (T_{λ_{2}} - T_{λ_{3}})^{2} + \dots + \\ (T_{λ_{n - 1}} - T_{λ_{n}})^{2} + (T_{λ_{n}} - T_{λ_{1}})^{2} = 0 \end{array}$ (9)

由于在测量过程中误差是不可避免的, 导致 $T_{λ_{1}}$ ≠ $T_{λ_{i + 1}}$ 的同时等式(9)也不成立, 因此将未知数构成的多元温差函数用式(10)表示

$\begin{array}{l} F = (T_{λ_{1}} - T_{λ_{2}})^{2} + (T_{λ_{2}} - T_{λ_{3}})^{2} + \dots + \\ (T_{λ_{n - 1}} - T_{λ_{n}})^{2} + (T_{λ_{n}} - T_{λ_{1}})^{2} \end{array}$ (10)

式(10)中, 未知数 $ε_{λ_{i}}$ 包含在由式(7)表示的 $T_{λ_{i}}$ (i=1, 2, …, n)中。由误差的相关知识可知, 多元温差函数值F越小即各通道测量的温度差就越小表示温度 $T_{λ_{i}}$ 越接近真温, 测温的精度也越高, 当F取到最小值0时, $T_{λ_{i}}$ 表示的真温唯一。但由于误差的存在, F很难取到最小值, 而在理论上极小值又有无穷多个, 因此, 多光谱温度反演问题转化成了多元函数极值优化问题。

1.2 不等式约束条件

由光谱测温的相关理论可知, 待测物体光谱发射率的范围在(0, 1)之间, 关系式如式(11)所示

$0 < ε_{λ_{i}} < 1$ (11)

这种约束关系虽然简单, 但制约了式(7)中 $T_{λ_{i}}$ 的取值范围, 提高了多元函数极值优化问题求解的速度, 构成了不等式约束条件。

2 多元极值优化法

将求解多元函数在不等式约束条件下最优化问题的方法称为多元极值优化法MEVO(multi-element extreme value optimization), 其基本结构形式如式(12)

$\{\begin{array}{l} \min f = {[AX + B - CX - D]}^{T} [AX + B - CX - D] \\ s . t . a \leq φ (X) \leq b \end{array}$ (12)

式(12)中, X∈ Rⁿ, A, B, C和D分别为n× n, n× 1, n× n, n× 1的矩阵。

通过上述1原理分析可知, 建立的多元温差函数和不等式约束条件与式(12)中多元极值优化法的形式一致。其中X表示由未知数 $ε_{λ_{i}}$ 构成的n维向量, minf表示优化多元温差函数极值, α ≤ φ (X)≤ b表示光谱发射率范围, 在真温反演过程中a=0, b=1。因此, 可以使用多元极值优化法求解优化多元温差函数的极小值, 实现多光谱真温反演问题向多元极值优化问题的转化。多元极值优化法代码可借助粒子群、梯度下降、神经网络等算法实现, 求解出多元函数极值后便可计算得到光谱发射率值, 将其重新代入多元温差函数进行二次寻优, 最终实现光谱发射率和真温的反演。

3 实验验证

为了验证提出的测温方法, 以火炸药瞬态燃烧温度辐射测量为例, 搭建了一套简单的8通道多谱测温装置, 其结构如图1所示。光谱仪将黑体炉产生的辐射分解成不同波长的光谱段并转化为电信号, 把光谱仪采集的多光谱数据传输至PC端进行温度求解。基于火炸药瞬态燃烧温渡高温分布范围, 将黑体炉温度分别设定为1 923.15、 1 973.15、 2 023.15、 2 073.15、 2 123.15、 2 173.15、 2 223.15和2 273.15 K, 待其温度稳定后, 将光谱仪在距离黑体炉窗口0.5 m处采集光谱数据。实验中认定黑体炉发射的温度是标准值, 在这种情况下对光谱数据进行标定。表1所示为光谱仪8个通道的有效波长以及各通道在参考温度1 923.15 K时的电压数据, 不同测量温度下各通道的电压数据如表2所示。

	Figure Option View Download New Window
	图1 实验结构图Fig.1 Diagram of experimental design

表1 参考温度下各通道电压数值 Table 1 Voltage value of each channel at reference temperature

表2 测量温度下各通道电压数值 Table 2 Voltage value of each channel under measurement temperature

采用Electro Optical公司生产的型号为LS3000-100的黑体炉作为标准辐射源用来标定系统。该黑体炉的辐射温度范围为1 000~3 000 ℃, 发射率为0.997± 0.002, 光谱辐射范围为0.2~11 μ m, 2 700 ℃以下的温度误差为0.25%; 采用Lenovo公司生产的型号为ThinkpadE540的PC机处理数据, 其处理器为Intel(R)Core(TM)i5-4210MCPU@2.60GHz2.59GHz, 安装内存为8.00 GB。

采用多元极值寻优的温度反演方法求解光谱发射率、反演温度并记录反演时间, 取8个通道测量温度的均值作为测量结果, 由表3可知, 本方法在1 923.15~2 273.15 K温度范围内, 测量误差基本在0.5%以内, 误差范围为0.07%~0.93%; 反演时间均小于2.5 s, 最快可达0.47 s。

表3 与SMM法反演结果对比 Table 3 Comparison of inversion results between the method proposed in this paper and SMM method

将本方法与二次测量法(secondary measurement method, SMM)进行比较, 从表3可知, 本方法相对SMM法精度有所提高, SMM法测量误差范围在0.05%~2.07%之间; 而在反演时间上, SMM法所用时间都在55S以上, 而本方法在完全相同的条件下反演时间都减小到2.5 s以内, 反演速度有了大幅度提高。

表3中, 测量误差=|反演温度-黑体炉温度|÷ 黑体炉温度; SMM法在给定1个温度初值的情况下可同时获取2个温度点的测量温度, 实验中SMM法温度初值选在高于第1温度点20 K处, 即分别在1 943.15、 2 043.15、 2 143.15和2 243.15 K处4个温度点测量, 获取8个测量温度, SMM法测量数据与本方法数据均取自黑体炉辐射的光谱数据且两种方法均在同一台PC机上运行, 实验条件完全相同。

将本方法与基于神经网络的测温方法进行比较, 结果如表4所示。从表4的对比结果可知, 本方法在1 923.15~2 273.15 K温度范围内, 测量误差均小于基于神经网络方法的测量误差, 说明在1 923.15~2 273.15 K温度范围内本方法的测温精度要高于基于神经网络测温方法; 在测温时间方面, 神经网络需要大量的数据进行训练, 导致数据处理耗时过长, 不具有比较意义。

表4 与神经网络方法反演结果对比 Table 4 Comparison of inversion results between the method proposed in this paper and the neural network method

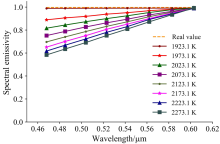
图2为不同温度下利用本方法求解的光谱发射率随波长变化的曲线图。图中Real value表示真实的光谱发射率随波长变化的曲线。

	Figure Option View Download New Window
	图2 光谱发射率随波长变化趋势Fig.2 Variation trend of spectral emissivity with wavelength

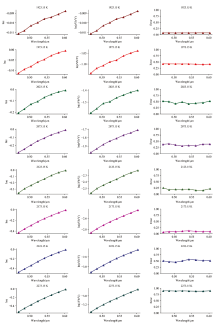由图2可知, 实验求解的光谱发射率存在较大误差, 但实验求解的温度误差却很小; 因此对本实验的结果进行误差分析, 分析结果如图3所示。图中每一列分别表示不同温度下lnε , ln $(\frac{ε V_{b}}{V})$ 和测温误差随波长变化的曲线图, 由图中可以看出不同温度下lnε 和ln $(\frac{ε V_{b}}{V})$ 随波长的变化趋势保持一致, 而测温误差基本在一个非常小的范围内波动。

	Figure Option View Download New Window
	图3 误差分析: 不同温度下lnε , ln $(\frac{ε V_{b}}{V})$ , error与波长的关系Fig.3 Error Analysis: Relationships between, lnε , ln $(\frac{ε V_{b}}{V})$ , error and wavelength at different temperatures

根据多光谱辐射测温的基本理论以及式(7)的变形公式(13)可知, 式(13)中ln $(\frac{ε_{λ_{i}} V_{λ_{i} b}}{V_{λ_{i}}}) /$ C₂为误差项, 将C₂认定是常数的情况下误差项变为ln $(\frac{ε_{λ_{i}} V_{λ_{i} b}}{V_{λ_{i}}})$ , 结合图3分析可知: 本方法测温误差主要是由光谱发射率的测量结果导致的, 但误差项ln $(\frac{ε_{λ_{i}} V_{λ_{i} b}}{V_{λ_{i}}})$ 的变化值与比值C₂的数量级相差甚大, 使得本方法的测温误差在一个很小的范围内波动。如式(13)

$\frac{1}{T_{λ_{i}}} - \frac{1}{T_{rb}} = \ln [\ln (\frac{ε_{λ_{i}} V_{λ_{i} b}}{V_{λ_{i}}}) / C_{2}]$ (13)

通过上述实验设计, 本方法的可行性得到了验证。实验结果表明该方法与其他方法相比测温精度与反演速度均有所提高, 是一种较好的测温方法。

4 结论

基于多元极值优化的多光谱温度测量方法, 避免了由光谱发射率假设模型带来的误差, 同时降低了深度学习方法对数据样本量的要求, 将复杂的建模过程简化为多光谱温差的寻优问题, 提高了建模效率, 更便于工程中的应用。通过在1 923.15~2 273.15 K温区内建模实验表明, 与二次测量法、神经网络方法相比, 本方法的测温精度均有所提高, 反演精度在0.5%左右, 与二次测量法相比反演速度有大幅度提高, 温度反演时间在2.5 s以内。

参考文献

文献列表

[1]	Araujo A. Infrared Physics & Technology, 2016, 76: 365. [本文引用:1]
[2]	Yu Kun, Guo Huige, Zhang Kaihua, et al. Applied Optics, 2021, 60(7): 1916. [本文引用:1]
[3]	Gao Shan, Zhao Chunhui, Chen Liwei, et al. Measurement Science and Technology, 2021, 32(5): 055003. [本文引用:1]
[4]	Liang Mei, Sun Bojun, Sun Xiaogang, et al. Measurement, 2017, 95: 239. [本文引用:1]
[5]	Chen Liwei, Sun Shang, Gao Shan, et al. Infrared Physics and Technology, 2020, 111: 103523. [本文引用:1]
[6]	QIN Ya-lou, LI Wei, YANG Chun-ping, et al(秦亚楼, 李伟, 杨春平, 等). Acta Armamentarii(兵工学报), 2019, 40(1): 219. [本文引用:1]
[7]	ZHANG Lei, CHEN Shao-wu, ZHAO Hai-chuan, et al(张磊, 陈绍武, 赵海川, 等). Chinese Optics(中国光学), 2019, 12(2): 289. [本文引用:1]
[8]	XING Jian, MA Zhao, BAI Yan(邢键, 马召, 白岩). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(12): 3761. [本文引用:1]
[9]	Zhu Wenjie, Shi Deheng, Zhu Zunlue, et al. International Journal of Heat and Mass Transfer, 2017, 109: 853. [本文引用:1]
[10]	Wang Nian, Shen Hua, Zhu Rihong. Measurement, 2020, 170: 108725. [本文引用:1]
[11]	Suleiman Fatima K, Lin Kaihsiang, Daun Kyle J. Journal of Quantitative Spectroscopy and Radiative Transfer, 2021, 271: 107693. [本文引用:1]
[12]	Liu H, Zheng S, Zhou H, et al. Measurement Science & Technology, 2016, 27(2): 025201. [本文引用:1]
[13]	ZHAO Yu-qing, LI Jian-qiang, SHENG Peng, et al(赵玉清, 李建强, 盛鹏, 等). Journal of Ordnance Equipment Engineering(兵器装备工程学报), 2021, 42(11): 146. [本文引用:1]
[14]	ZHANG Fu-cai, SUN Xiao-gang, XING Jian, et al(张福才, 孙晓刚, 邢键, 等). Infrared and Laser Engineering(红外与激光工程), 2016, 45(7): 39. [本文引用:1]
[15]	SUN Hong-sheng, LIANG Xin-gang, MA Wei-gang, et al(孙红胜, 梁新刚, 马维刚, 等). Infrared and Laser Engineering(红外与激光工程), 2021, 50(5): 36. [本文引用:1]
[16]	XI Jian-hui, JIANG Han, CHEN Bo, et al(席剑辉, 姜瀚, 陈博, 等). Journal of Shanghai Jiao Tong University(上海交通大学学报), 2021, 55(7): 891. [本文引用:1]

2016

0.0