引用本文
薛方家, 喻洁, 尹航, 夏戚宇, 施杰根, 侯迪波, 黄平捷, 张光新. 基于三维荧光时间序列双阈值的饮用水污染事件检测方法研究[J]. 光谱学与光谱分析, 2023,43(10): 3081-3088.
XUE Fang-jia, YU Jie, YIN Hang, XIA Qi-yu, SHI Jie-gen, HOU Di-bo, HUANG Ping-jie, ZHANG Guang-xin. A Time Series Double Threshold Method for Pollution Events Detection in Drinking Water Using Three-Dimensional Fluorescence Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2023,43(10): 3081-3088.
Doi:10.3964/j.issn.1000-0593(2023)10-3081-08  
Permissions
Copyright©2023, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于三维荧光时间序列双阈值的饮用水污染事件检测方法研究
薛方家, 喻洁*, 尹航, 夏戚宇, 施杰根, 侯迪波, 黄平捷, 张光新
浙江大学控制科学与工程学院, 工业控制技术国家重点实验室, 浙江 杭州 310058
*通讯作者 e-mail: yu_jie@zju.edu.cn

作者简介: 薛方家, 1999年生, 浙江大学控制科学与工程学院硕士研究生 e-mail: 22132007@zju.edu.cn

收稿日期: 2022-06-14 修回日期: 2022-09-29
基金: 浙江省重点研发计划项目(2021C03177, 2022C03078), 国家自然科学基金青年科学基金项目(61803333), 国家自然科学基金联合基金项目(U21A20519)资助
摘要

目前, 三维荧光技术在应急性饮用水污染事件检测中的应用越来越广泛, 但其仍存在易受水环境波动影响、 低浓度污染事件检出率较低等不足。 因此针对在线检测需求, 提出了一种基于时间序列双阈值的三维荧光饮用水异常事件检测方法。 该方法采用主成分分析法提取检测样本的三维荧光光谱主元特征值, 进行线性自回归(AR)模型训练并对未来时段水质样本主元特征值进行预测, 通过与实测样本主元特征值作差得到特征值差值, 同时结合实测特征值的变化率, 设置特征值差值-特征值变化率双阈值, 最终确定污染事件的时间起始点与结束点, 从而确定整个污染事件。 研究通过模拟高浓度污染事件、 低浓度污染事件、 供水水质波动等场景对所提方法进行了验证。 实验结果表明, 该方法不仅保持了高浓度污染事件检测的准确性, 在检测低浓度污染、 高干扰环境下的低浓度污染时, 该方法相较于常规判别方法, 检测结果准确率分别提高了9.4%和20.7%。

关键词: 水质异常事件检测; 三维荧光光谱; 时间序列双阈值; 主成分分析(PCA); 线性自回归(AR)
中图分类号:O657.3 文献标志码:A
A Time Series Double Threshold Method for Pollution Events Detection in Drinking Water Using Three-Dimensional Fluorescence Spectroscopy
XUE Fang-jia, YU Jie*, YIN Hang, XIA Qi-yu, SHI Jie-gen, HOU Di-bo, HUANG Ping-jie, ZHANG Guang-xin
State Key Laboratory of Industrial Control Technology, College of Control Science and Engineering, Zhejiang University, Hangzhou 310058, China
*Corresponding author
Abstract

Three-dimensional fluorescence technology is attracting attention in detecting emergency drinking water pollution events. However, some unsolved problems remain, such as being easily affected by water environment fluctuations, low detection rate facing low-concentration organic pollutants, etc. Therefore, in response to the demand for online monitoring, this study proposed a time series double thresholds method for anomaly detection in drinking water using three-dimensional fluorescence. This method applied principal component analysis (PCA) to extract the feature spectrum of the detected samples and trained the linear autoregressive (AR) model to predict the principal component of the water samples in the future. The eigenvalue difference was then obtained by comparing the predicted and measured ones. At the same time, combined with the change rate of the measured eigenvalues, the double threshold for time series was set to finally determine the start and end points of the pollution event to determine the entire pollution event. The research validated the proposed method by simulating high-concentration pollution events, low-concentration pollution events, and fluctuations in water background. The experimental results show that this method maintains the detection accuracy for high-concentration pollution events. Moreover, compared with conventional methods, the proposed method improved the detection performance in low-concentration pollution events and low-concentration pollution in high-interference environments. The detection accuracy is increased by 9.4% and 20.7%, respectively.

Keyword: Water pollution incident detection; Three dimensional fluorescence spectroscopy; Time series double threshold; Principal component analysis (PCA); Linear autoregression (AR)
引言

供水安全是国家安全中极为重要的一环, 它是社会正常运作的重要保障之一[1]。 近几十年来, 虽然随着公民素质的提高, 生活废水对水体的污染事件明显减少, 但是偷排工业废水仍数见不鲜, 突发性污染事故更是频频发生。 根据对国内水污染事件的统计, 污染环节主要发生在水源污染、 管网污染以及二次供水污染, 且污染原因以化学性污染为主, 其中有机物污染尤为严重[2]。 因此为了减少突发性污染产生的损失, 迫切需要一种更加快捷实时的水质检测方法。

饮用水污染检测的常用方法有化学分析法[3]、 气相色谱法[4]、 质谱法[4]、 光谱法[5]等方法。 相较于其他方法, 光谱法无需复杂且耗时的样品富集、 化学试剂添加和其他预处理操作, 具有仪器成本更低、 检测操作更简单、 检测结果获取更快速、 无二次污染等优点。 此外, 三维荧光灵敏度高、 信息丰富, 能够更有效地检测低浓度有机物污染, 并对污染物进行识别[6, 7, 8]。

近年来, 三维荧光光谱越来越多地被应用于饮用水污染检测、 城市供水突发污染检测与预警中。 Peiris[9]等利用主成分分析法(PCA)对三维荧光原始数据进行特征提取, 根据提取的特征值对超滤和纳滤饮用水的系统性能进行检测, 实现了对饮用水处理过程中膜污染事件的预警; Heibati[10]等采用平行因子法(PARAFAC)对饮用水的三维荧光数据进行特征提取, 发现溶解有机物(DOM)的荧光组分能够反映饮用水是否受到污染。 PCA和PARAFAC能够有效提取三维荧光光谱图中的信息, 使得三维荧光检测方法能够检测水体中的污染物, 但也存在一定的局限性: 由于在特征提取过程中, 对三维荧光光谱数据进行线性化处理, 会损失部分特征信息因此在检测低浓度污染物时, 难以有效区分低强度荧光峰与外界干扰[11]。 而饮用水中出现有机污染物质的浓度大多较低(μg· L-1级别), 因此常规的基于PCA和PARAFAC的水质异常检测方法较难实现饮用水突发性污染的有效检测。

为了解决PCA和PARAFAC对低浓度污染物检出率低的问题, 许多学者提出了其他荧光分析方法来弥补这一缺陷。 Huang[12]等使用2-D Gabor小波从三维荧光光谱中提取特征, 并将其与SVM结合以识别水中存在的污染物; Yu[13]等采用了对PARAFAC方法进行改进的三线性分解(ATLD)方法来分析正常饮用水样品的特征, 通过残差矩阵、 阈值方法使研究人员能够确定饮用水是否受到污染; 陈方[14]等通过设计了不同环境下的实验, 对不同水质环境得到的水样本进行分析, 对比了基于残差平方, 奇异值分解和三线性分解模型三种特征提取方法, 通过对比不同方法在不同水环境中的效果, 提高了三维荧光水质检测在不同污染环境下的准确率。 这些方法虽然有效提高了饮用水中低浓度污染物的检出率, 但是对饮用水背景波动缺乏适应性。 饮用水三维荧光光谱(背景光谱)会随着时间、 外界环境变化等各种干扰, 不断发生变化。 在检测低浓度污染时, 传统特征提取结合分类器的方法由于未考虑三维荧光光谱在时间维度上的相关性, 易受到背景波动和外界干扰, 进而造成误报和漏报。

饮用水背景变化造成的外界干扰, 可以分为周期性干扰与随机性干扰。 在时间序列上, 干扰与真正污染发生时的三维荧光特征值变化情况存在明显区别: 周期性干扰发生时, 特征值周期性超出阈值范围; 随机性干扰发生时, 特征值表现出突然上升突然下降的特点, 同时突发性污染事件特征值常存在持续上升, 趋于平稳, 持续下降的过程。 基于外界干扰与实际污染在时间维度上不同的表现, 可以对时间序列三维荧光数据进行时间序列分析, 实现污染事件的检测。 此前, 于绍慧[15]等利用时间维和光谱维的内在特性, 采用时间维补偿矩阵和相邻时段三维荧光矩阵的累计相似度, 对按时间顺序排列的三维荧光光谱数据中的异常值进行了检测。 采用时间序列累积的方法, 虽然能放大异常值的三维荧光信息, 但同样会放大外界干扰, 难以有效区分外界干扰与实际污染事件。

针对上述问题, 本文提出了一种将三维荧光与时间序列异常检测相结合的方法, 该方法不仅能检测饮用水体中的低浓度有机物污染, 更加能够解决低浓度污染事件检测过程中饮用水背景波动的问题。 本方法先采用主成分分析法提取三维荧光光谱的前两个主元特征值, 训练线性自回归(AR)模型并对未来时段主元特征值进行预测, 与实测主元特征值作差得到特征值差值, 用于排除周期性干扰的影响; 并对实测特征值变化率进行计算, 用于排除随机性干扰的影响。 最终设置特征值差值-特征值变化率双阈值确定污染的起始点与结束点, 从而确定整个污染事件。 并且设计实验, 选取苯酚作为模拟污染物, 分别模拟了高浓度有机物突发性污染、 低浓度有机物突发性污染以及饮用水背景大幅度波动下的低浓度有机物突发性污染, 并将时间序列双阈值方法与传统的三维荧光检测方法在检测准确率上进行了对比, 证明了方法的有效性。

1 实验部分
1.1 实验设计

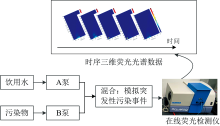
为了证实本文提出的时间序列双阈值法对饮用水特征污染物进行定性判别检测的有效性, 本文搭建了饮用水污染模拟事件检测系统, 如图1所示, 其包含了污染模拟系统和光谱检测系统。 污染模拟系统中, 饮用水和污染物分别由A、 B泵抽取混合, 模拟突发性污染事件, 并可以通过改变双泵流量, 实时控制污染物浓度; 光谱检测系统中, 荧光测量仪器采用Horiba公司的Aqualog为检测设备, 激发波长设置范围为240~800 nm, 发射波长设置范围为243.544~823.84 nm, 积分时间0.1 s, 每90 s就可以实现一次三维荧光光谱采样, 可以得到时间序列三维荧光光谱数据。

图1 实验装置示意图Fig.1 Schematic diagram of experimental device

在污染物选取方面, 苯酚作为饮用水中常见的污染物, 已经被我国《生活饮用水卫生标准》(GB5749—2022)列为生活饮用水水质的扩展指标[16], 因此实验选取苯酚作为模拟污染物, 依据《生活饮用水卫生标准》(GB5749—2022)中苯酚限值, 设计了三组不同环境下模拟突发性污染实验进行验证。

第一组实验用于模拟突发性污染发生在检测点附近的高浓度污染事件, 实验中苯酚浓度梯度设置为40~200 μg· L-1, 共5个污染事件, 实验共进行120 min, 获得三维荧光光谱数据35个。

第二组实验用于模拟突发性污染发生点距离检测点较远, 由扩散导致的低浓度污染事件, 实验中苯酚浓度梯度设置为5~20 μg· L-1, 共3个污染事件, 获得三维荧光光谱数据85个。

第三组实验选用sipper实验装置直接从管道取水, 由于sipper装置内水流量不断发生变化, 外界干扰也明显大于之前两组实验, 与真实管道相类似, 用于模拟水质背景波动下的低浓度污染事件, 实验中苯酚浓度设置为2 μg· L-1, 共1个污染事件, 获得三维荧光光谱数据137个, 其中前40个数据点用于训练AR模型, 后97个数据点用于测试算法有效性。

1.2 方法

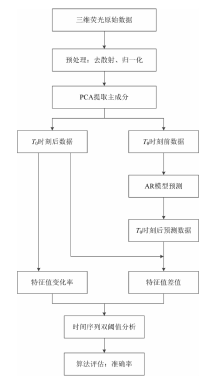
算法的流程如图2所示, 预处理实验数据得到的三维荧光在线数据, 使用主成分分析法(PCA)进行降维得到主元特征值数据, 之后通过线性自回归(AR)方法进行特征值预测, 得到特征值差值与特征值变化率, 根据设定的阈值确定污染事件起始和结束点, 从而确定整个污染事件, 并将检测的准确率与支持向量机检测结果, 以及基于支持向量机(SVM)的时间序列修正结果进行对比, 对算法进行评估。

图2 方法流程图Fig.2 Algorithm framework diagram

1.2.1 数据预处理

从三维荧光仪器中得到的数据, 需要经过去散射和归一化预处理:

(1)去散射: 在三维荧光光谱的测量中, 由于复杂的能级跃迁, 瑞利散射和拉曼散射同时发生, 散射光的干扰严重影响了光谱的灵敏度及光谱数据分析[17], 会对污染物检测造成影响, 而通过去散射可以使污染物的特征峰更加明显, 增强污染检测的精度。 本文采用插值法对原始光谱数据进行预处理来减少瑞利散射对检测的影响, 并采用扣除空白溶剂背景的方法消除拉曼散射的影响。

(2)归一化: 三维荧光仪测得的三维荧光光谱数据会出现小于0的情况, 三维荧光强度并不会小于0, 因此属于误报, 需要将三维荧光数据小于0的值改成0。 而对于不同时间获得的水样, 容易受到温度, 湿度以及其他外界环境干扰造成数据不统一, 因此在完成每组实验之前先检测纯水水拉曼值, 每组数据除以当日的水拉曼值后进行归一化处理。 在水拉曼处理后, 再进行标准化处理此处采用min-max标准化, 其数学表达式如式(1)所示

X'=X-data_mindata_max-data_min(1)

式(1)中, X'为归一化处理后的数据, X为原数据, data_max为三维荧光数据中的最大值, data_min为三维荧光数据中的最小值。

1.2.2 主成分分析法

主成分分析法(PCA)[18]是一种数据降维算法, 通过正交变换将一组存在相关性的变量转换为一组线性不相关的变量, 转换后的这组变量称为主成分, 主成分按其方差大小排序, 第一成分含有原始数据最多的信息, 第二成分含原始数据次多信息, 依次类推, 保留低阶主成分就等同于保留了原始数据主要特征信息。 假设有m个n维向量xi, 它们之间存在一定相关性, 要提取它们主要特征信息, PCA算法实现如下:

(1)将向量按行组成矩阵X=[x1, x2, ···, xm]T, 对每行进行零均值处理, X~=X- X-, 其中 X-为X的均值。

(2)计算 X~的协方差矩阵, C= X~TX~。

(3)取前k阶主成分, Y= UkTX~, 其中U为C的特征矩阵, Y为提取到的主成分, 各主成分贡献率可以通过C的对角矩阵得到。

1.2.3 特征值差值-特征值变化率双阈值方法

特征值差值-特征值变化率双阈值算法基于干扰与真实污染事件不同的特点进行设计, 在时间全维度上, 外界干扰发生时特征值表现出突然上升突然下降的特点, 而突发性污染事件发生时特征值常有持续上升, 趋于平稳, 持续下降的过程。 其具体判断流程如下:

(1)采用线性自回归模型计算得到每个时间点的特征值预测值Y't

Y't=c0+c1Y't-1+c2Y't-2+···+ciY't-i+εt(2)

式(2)中, Y't是线性自回归模型预测值, Y't-i为i个时间点之前的预测值, c0为常数项, ε t为加入的高斯白噪声。

(2)根据主成分分析法得到的特征值Yt, 得到各时间点的特征值差值 Y~t, 以及该时间点和下一时间点的特征值变化率Qt和Qt+1

Y~t=|Y't-Yt|Qt=(Yt-Yt-1)/ΔtQt+1=(Yt+1-Yt)/Δt(3)

式(3)中, Δ t为三维荧光光谱采样间隔时间。

(3)通过判断特征值差值 Y~t, 以及该时间点和下一时间点的特征值变化率Qt和Qt+1是否超过阈值, 从而确定该时间点是否发生污染, 污染起始点判断如式(4)所示

Y~t< P, 无污染Y~t> P, 判断一下参数Qt< Q1, 无污染Qt> Q1, 判断一下参数Qt+1< Q2, 无污染Qt+1> Q2, 存在污染(4)

式(4)中, P, Q1, Q2分别为特征值差值以及特征值变化率的阈值, 本文中, P=0.5, Q1=0.5 min-1, Q2=-0.5 min-1。

依照以上算法, 可以对污染发生和结束点进行准确判断, 从而确定整个污染事件, 算法对污染起始点的判断逻辑框架图如图3所示。

图3 算法逻辑框架图Fig.3 Algorithm logic framework diagram

2 结果与讨论
2.1 高浓度污染检测结果

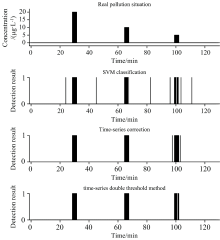
高浓度污染检测结果如图4所示, 可以看出, 由于污染物浓度较高, 各方法都能很好地检测出突发性污染事件。 该实验用于模拟突发性污染发生在污染监测点附近的情况, 苯酚浓度梯度设置为40~200 μg· L-1, 共设置5个污染事件, 各个事件苯酚浓度分别为200、 160、 120、 80和40 μg· L-1。

图4 高浓度污染检测结果Fig.4 High-level pollution test results

2.2 低浓度污染检测结果

低浓度污染检测结果如图5所示, 可以看出, 传统SVM分类由于低浓度苯酚的三维荧光光谱特征峰较低, 容易与自来水中受外界干扰出现的干扰峰相混淆, 因此出现大量低浓度苯酚污染被误报的情况。 该实验用于模拟突发性污染发生点距离检测点较远, 由扩散导致的低浓度污染事件, 实验中苯酚浓度梯度设置为5~20 μg· L-1, 共3个污染事件。

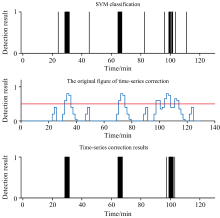
图5 低浓度污染检测结果Fig.5 Low-level pollution test results

对于低浓度的突发性污染中传统SVM分类结果进行分析后可以发现, 很多误报漏报点都以孤立的形式出现, 如图6, 在低浓度污染检测结果中, A、 B、 C点就是明显的误报漏报点。 可以根据时间序列上SVM对前后几个时间点是否发生污染的分类结果, 对该点是否存在污染进行重新判断, 如式(5)所示

rt=0.4ct+0.2ct-1+0.2ct-2+0.2ct+1rt> 0.5, 则取rt=1rt< 0.5, 则取rt=0(5)

图6 低浓度污染检测误报点Fig.6 False alarm point of low-level pollution test

式(5)中, ct为原分类结果, rt为修正值, 1代表存在污染, 0代表无污染。

时间序列修正的过程如图7所示, 经过简单的时间序列修正, 如表1所示, 低浓度污染检测结果准确率明显上升。

图7 时间序列修正过程图Fig.7 Time-series correction process

表1 修正准确率对比 Table 1 Correction accuracy comparison
2.3 水质背景波动下的低浓度污染检测结果

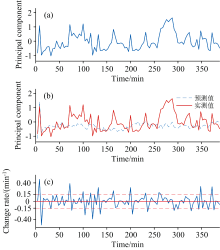
水质背景波动选取模拟真实管道作为实验对象, 在水流量不断变化、 高外界干扰的情况下, 实验中饮用水背景三维荧光光谱图在外界干扰下不断发生变化, 如图8所示, 四张图均为无污染发生时的正常饮用水背景三维荧光光谱图, 但是其特征峰明显存在不同, 因此PCA提取得到的主元特征值也随着时间不断变化, 如图10(a)所示, 无法采用SVM对污染事件和背景波动正常值进行有效区分。

图8 水质背景三维荧光光谱波动图
(a)—(d)为不同时间段的饮用水光谱图Fig.8 Three dimensional fluorescence spectrum fluctuation of water quality background
(a)—(d) are the EEM of drinking water in different time periods

在这种环境中, 各算法检测结果如图9所示, 可以看出, 在高干扰和污染物浓度很低的情况下, 传统SVM方法出现大量误报和漏报, 难以有效检测污染事件。

图9 水质背景波动下的低浓度污染检测结果Fig.9 Low concentration pollution detection results under fluctuating water quality background

因此需要对高干扰环境使用时间序列双阈值方法进一步改善准确性。 以主元贡献率最高的两个特征值为对象, 建立线性自回归模型, 综合考虑主元特征值阈值与变化率进行异常检测。 此处将前40个未发生污染的数据选作训练集, 选取其PCA贡献度最高的两个主元作为输入, 经过最小二乘法, 确定AR模型如式(6)所示, 其中贡献度最高的主元特征值预测结果与实测值对比图如图10(b)所示, 主元特征值变化率如图10(c)所示

Y't=0.4Y't-1+0.25Y't-2+0.15Y't-3+0.1Y't-4+0.1Y't-5+εt(6)

式(6)中, Y't是线性自回归模型预测值, Y't-i为i个时间点之前的预测值, ε t为加入的高斯白噪声。

图10 主元特征值图像
(a): 主元特征值变化曲线; (b): 正常水背景主元特征值预测结果; (c): 主元特征值变化率Fig.10 The image of principal component
(a): The change curve of principal component; (b): The prediction result of principal component in the normal water background; (c): The change rate of principal component

从预测与实测值曲线可以看出, 在未发生污染事件时, 预测结果与实测值拟合效果较好, 污染发生后, 两者出现了明显的偏差, 先采用阈值法对苯酚污染进行检测, 综合考虑第一主元与第二主元, 预测值与实测值差值计算公式如式(7)所示

Y~1=|Y'1-Y1|Y~2=|Y'2-Y2|Y~=(c1Y~1)2+(c2Y~2)2(7)

式(7)中, Y~1与 Y~2分别为前两个主元的特征值差值, Y~为特征值差值计算结果, c1为第一主元贡献度, 根据PCA结果取c1=7.96; c2为第二主元贡献度, 根据PCA结果取c2=0.82。 依据特征值差值与特征值变化率对突发性污染进行检测, 得到检测结果如表2所示。

表2 双阈值检测准确率对比 Table 2 Comparison of double threshold detection accuracy

如表3所示, 高干扰环境采用时间序列双阈值检测方法后, 检测准确率相较简单的时间序列修正上升了11.4%, 尤其是对非边缘的误报区有了很大程度的改善, 能够有效地将污染事件与水样本身波动区分开来, 检测背景波动较大环境下的低浓度污染事件。

表3 不同算法在不同环境下准确率对比表 Table 3 Comparison table of accuracy of different algorithms in different environments
3 结论

针对三维荧光方法检测低浓度污染物质时, 传统判别方法容易受到水样本身波动以及检测设备噪声等影响, 进而产生污染事件误报和漏报等不足, 提出了一种基于时间序列双阈值法的三维荧光水质异常事件检测模型, 通过挖掘三维荧光数据时间维度信息, 设置特征值差值、 特征值变化率阈值, 有效解决了三维荧光在污染检测过程中受水质背景波动影响等问题。 实验结果表明, 该方法不仅在高浓度污染事件中检测准确, 在低浓度污染、 水质背景波动下的低浓度污染检测中, 准确率分别达到了98.8%和99.0%, 相较于传统的判别方法, 检测准确率明显上升, 说明本方法可以有效检测水质背景波动下的低浓度污染事件, 为三维荧光在线监测饮用水的有机物突发性污染提供了帮助。

参考文献
[1] LIN Jing-xue, LI Bao-zhi, REN Da-sheng, et al(林景雪, 李宝志, 任达生, 等). Chemical Analysis and Meterage(化学分析计量), 2017, 26(1): 118. [本文引用:1]
[2] TAN Li-feng, CHU Su-chun, HUI Gao-yun, et al(谈立峰, 褚苏春, 惠高云, 等). Journal of Environment and Health(环境与健康杂志), 2018, 35(9): 827. [本文引用:1]
[3] Liu Y H, Chen Y, Feng M J, et al. Environmental Science and Pollution Research, 2021, 28(31): 42339. [本文引用:1]
[4] Vizioli B D, Hantao L W, Montagner C C. Environmental Science and Pollution Research, 2021, 28(25): 32823. [本文引用:2]
[5] Wu M F, Wang X, Niu G H, et al. Analytical Chemistry, 2021, 93(29): 10196. [本文引用:1]
[6] Quintana J B, Carpinteiro J, RodrGuez I, et al. Journal of Chromatography A, 2004, 1024(1-2): 177. [本文引用:1]
[7] WANG Xiao-xue, WU Ba-yi(王晓雪, 吴八一). Resources Economization & Environmental Protection(资源节约与环保), 2014, (3): 91. [本文引用:1]
[8] JIANG Chuan(江川). Resources Economization & Environmental Protection(资源节约与环保), 2014, (4): 59. [本文引用:1]
[9] Peiris R H, Hallé C, Budman H, et al. Water Research, 2010, 44(1): 185. [本文引用:1]
[10] Heibati M, Stedmon C A, Stenroth K, et al. Water Research, 2017, 125: 1. [本文引用:1]
[11] Yu J, Cao Y, Shi F, et al. Water, 2021; 13(19): 2633. [本文引用:1]
[12] Huang P, Mao T, Yu Q, et al. Opt. Express, 2019, 27: 5461. [本文引用:1]
[13] Yu J, Zhang X, Hou D, et al. Journal of Spectroscopy, 2017, 2017: 1485048. [本文引用:1]
[14] CHEN Fang, ZHANG Xiao-yan, HUANG Ping-jie, et al(陈方, 张晓燕, 黄平捷, 等). Journal of Zhejiang University Agriculture and Life Sciences(浙江大学学报·农业与生命科学版), 2016, 42(3): 368. [本文引用:1]
[15] YU Shao-hui, ZHANG Yu-jun, ZHAO Nan-jing(于绍慧, 张玉钧, 赵南京). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(6): 1624. [本文引用:1]
[16] National Stand ard of the People's Republic of China(中华人民共和国国家标准). GB 5749—2022 Stand ards for Drinking Water Quality(生活饮用水卫生标准). National Health Commission of the People's Republic of China(中华人民共和国国家卫生健康委员会), 2022. [本文引用:1]
[17] Yu S, Xiao X, Xu G. Journal of Applied Spectroscopy, 2016, 83(5): 786. [本文引用:1]
[18] Bro R, Smilde A K. Analytical Methods, 2014, 6(9): 2812. [本文引用:1]