引用本文
陈勇, 郭云柱, 王威, 武小红, 贾红雯, 武斌. 模糊K-Harmonic-Kohonen网络的FTIR光谱数据聚类分析. 光谱学与光谱分析, 2023,43(1): 268-272
CHEN Yong, GUO Yun-zhu, WANG Wei, WU Xiao-hong, JIA Hong-wen, WU Bin. Clustering Analysis of FTIR Spectra Using Fuzzy K-Harmonic-Kohonen Clustering Network. Spectroscopy and Spectral Analysis, 2023,43(1): 268-272.  
Doi: 10.3964/j.issn.1000-0593(2023)01-0268-05
Permissions
Copyright©2023, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
模糊K-Harmonic-Kohonen网络的FTIR光谱数据聚类分析
陈勇1,2, 郭云柱1, 王威3,*, 武小红1,2,*, 贾红雯4, 武斌4
1. 江苏大学电气信息工程学院, 江苏 镇江 212013
2. 江苏省农业装备与智能化高技术研究重点实验室, 江苏 镇江 212013
3. 浙江大学台州研究院, 浙江 台州 317700
4. 滁州职业技术学院信息工程系, 安徽 滁州 239000
*通讯作者 e-mail: wangwei2@126.com; wxh-www@163.com

作者简介: 陈 勇, 1975年生,江苏大学电气信息工程学院讲师 e-mail: chenyong945@163.com

收稿日期: 2022-01-02 接受日期: 2022-03-30
基金项目: 国家自然科学基金项目(31471413),江苏高校优势学科建设工程项目(PAPD),滁州职业技术学院校级自科重点项目(YJZ-2020-12),滁州职业技术学院院级人才项目“优秀骨干教师”项目(YG2019026, YG2019024),江苏大学大学生科研立项课题(19A083)资助
摘要

食品的品种不同则其含有营养成分和功效存在差异, 得到的傅里叶变换红外光谱也存在差异。 为了准确的实现品种分类, 设计了一种将傅里叶变换红外光谱与模糊聚类分析方法相结合的品种鉴别方法。 在模糊Kohonen聚类网络(FKCN)基础上将模糊K调和聚类(FKHM)引入到Kohonen聚类网络的学习速率和更新策略中, 提出了模糊K-Harmonic-Kohonen网络(FKHKCN)算法。 FKHKCN利用模糊C均值(FCM)聚类的模糊隶属度计算其学习速率, 以FKHM的聚类中心为基础通过推导计算得到FKHKCN的聚类中心, 可以解决模糊Kohonen聚类网络方法对于初始类中心敏感而导致聚类结果不稳定的问题。 FKHKCN作为一种模糊聚类算法, 可实现傅里叶变换红外光谱数据的聚类分析。 采用三种数据集: (1)采集产自四川的三种茶叶(优质和劣质的乐山竹叶青以及峨眉山毛峰)作为实验样本, 样本总数为96。 (2)两个品种(robusta和arabica)的咖啡样本。 (3)三个品种(鸡肉、 猪肉和火鸡)的肉类样本。 首先对三个光谱数据集进行预处理, 利用多元散射校正降低茶叶样本原始光谱数据集的散射影响, 使用Savitzky-Golay减少噪声对肉类和咖啡这两个光谱数据集的影响。 再利用主成分分析将高维的三种光谱数据集压缩至低维。 然后采用线性判别分析进行特征提取, 将光谱数据投影到求得的鉴别向量上。 最后分别采用FCM, FKCN和FKHKCN对茶叶、 肉类和咖啡进行判别。 最终结果如下: FCM, FKCN和FKHKCN对茶叶品种的聚类准确率分别为90.91%, 90.91%和93.94%; 对肉类品种的聚类准确率分别为90.83%, 0.00%和92.50%; 对咖啡品种的聚类准确率分别为89.17%, 89.17%和90.83%。 以上实验结果表明: 采用傅里叶红外光谱技术结合主成分分析、 线性判别分析和FKHKCN的方法能够较有效地对食品的品种进行鉴别, 且鉴别准确率比FCM和FKCN更高, 聚类结果更稳定。

关键词: 傅里叶变换红外光谱; 模糊K调和均值聚类; 多元散射校正; 模糊Kohonen聚类网络; 聚类分析
中图分类号:TP391 文献标识码:A
Clustering Analysis of FTIR Spectra Using Fuzzy K-Harmonic-Kohonen Clustering Network
CHEN Yong1,2, GUO Yun-zhu1, WANG Wei3,*, WU Xiao-hong1,2,*, JIA Hong-wen4, WU Bin4
1. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China
2. High-tech Key Laboratory of Agricultural Equipment and Intelligence of Jiangsu Province, Jiangsu University, Zhenjiang 212013, China
3. Research Institute of Zhejiang University-Taizhou, Taizhou 317700, China
4. Department of Information Engineering, Chuzhou Polytechnic, Chuzhou 239000, China
*Corresponding authors
Abstract

Different foods contain different nutrients and effectiveness, and there are differences in their Fourier transform infrared spectra. In order to classify varieties of foods correctly, this paper presented the way to classify varieties by combining Fourier transform infrared spectroscopy (FTIR) with fuzzy clustering analysis. Fuzzy K-harmonic Kohonen clustering network (FKHKCN) was proposed by introducing fuzzy K-harmonic means (FKHM) clustering into the learning rate and update strategy of the Kohonen clustering network. The learning rate of FKHKCN is computed by fuzzy membership values of fuzzy C-means (FCM) clustering, and the cluster centers of FKHKCN can be derived from the cluster centers of FKHM. Therefore, FKHKCN can solve the problem that the Fuzzy Kohonen clustering network (FKCN) is sensitive to the initial cluster centers, and the clustering result is unstable. FKHKCN can achieve the clustering analysis of FTIR data as a fuzzy clustering algorithm. This experiment involves three datasets: (1) Three kinds of tea samples (Emeishan Maofeng, good and poor Leshan trimeresurus) were obtained from Sichuan, China as experimental samples with a total number of 96. (2) Two kinds of coffee samples (robusta and arabica). (3)Three meat samples (chicken, pork and turkey). To start with, three datasets were preprocessed. Scattering effects in the original spectra data of tea samples were reduced by multiple scattering correction (MSC). Savitzky-Golay was used to reduce noise in FTIR spectra of coffee and meat samples. Secondly, the high dimensional FTIR data of three datasets were reduced to by the low dimensionaldata by principal component analysis (PCA). Thirdly, tea data after PCA were extracted by linear discriminant analysis (LDA) and the spectral data were projected into the obtained discriminant vectors. Finally, FCM, FKCN and FKHKCN were used to classify the three datasets, respectively. The experimental results showed that FCM, FKCN and FKHKCN achieved the clustering accuracies for the tea varieties with the values: 90.91%, 90.91% and 93.94%, respectively; the clustering accuracies for the meat varieties with the values: 90.83%, 0.00% and 92.50%, respectively; the clustering accuracies for the coffee varieties with the values: 89.17%, 89.17% and 90.83%, respectively. The above experimental results indicated that FTIR technology coupled with PCA, LDA and FKHKCN was an effective method for classifying food varieties, and its clustering accuracy was higher than FCM and FKCN, and its clustering result was stable.

Key words: FTIR; Fuzzy K-harmonic means clustering; Multiple scattering correction; Fuzzy Kohonen clustering network; Clustering analysis
引言

傅里叶变换红外光谱技术具有方便, 快捷, 适用范围广等优点。 中红外光谱的波数范围在4 000~400 cm-1之间, 大多数的无机化合物和有机化合物的化学键振动的基频均在此区域。 不同的分子中官能团、 化合物的类别和化合物的立体结构, 其中红外吸收光谱不尽相同。 不同品种的食品和农产品, 其组分及含量往往存在差别, 那么它们的中红外光谱存在差异。 根据这个原理, 可以用中红外光谱技术进行食品品种的准确分类[1, 2, 3]。

近年来, 国内外研究人员在应用傅里叶变换红外光谱进行农产品/食品检测的应用方面已经取得了一些成果。 例如: Cai等用傅里叶变换红外光谱结合偏最小二乘-自组织映射实现茶叶品种分类, 准确率达100%[4]。 Krahmer等利用ATR-FTIR光谱的聚类分析成功地将洋葱分为鲜市场洋葱、 贮藏洋葱和脱水洋葱[5]。 Cebi等利用傅里叶变换红外光谱(Fourier transform infrared spectroscopy, FTIR)、 拉曼光谱等结合化学计量学成功鉴别出真实的大黄精油样品和虚假的商业样品[6]。 Freitas等建立了用FTIR法直接测定奶粉中泰乐菌素残留量的方法[7]。 Ciursa等采用支持向量机和偏最小二乘判别分析对FTIR进行了不同的光谱预处理, 以提高真假蜂蜜的鉴别能力[8]。 Silva等利用FTIR分析法对填充乳液的水凝胶进行化学和物理结构评价, 并对水凝胶模拟消解后的形态进行评价[9]。 Labaky等通过原位FTIR的创新技术和流变仪以及结合颗粒尺寸测量、 小变形流变学, 对芒果泥及其分散相的粒径和流变性能进行了广泛的研究[10]。 Wang等利用FTIR和化学计量测量相结合的方法来区分牛奶热处理程度的新方法[11]。 以上的研究结果表明, 利用傅里叶变换红外光谱技术能够有效地对农产品或者食品的品质进行检测和分类[12, 13]。

模糊C-均值聚类(fuzzy c-means, FCM)是一种十分常用的聚类算法, 在农产品检测方面有着十分广泛的应用。 例如Wu等利用模糊C-均值聚类算法结合模糊线性判别分析算法对苹果的品种进行分类[14]。 但是, 由于FCM存在着对初始聚类中心敏感问题而导致聚类结果不稳定。 即使是将FCM引入到Kohonen聚类网络的学习速率和更新策略中后而得到的模糊Kohonen聚类网络(fuzzy Kohonen clustering network, FKCN), 同样也存在着与FCM相同的问题。 K调和均值聚类(K-harmonic means, KHM)是一种基于中心的迭代聚类方法[15]。 KHM将所有数据点到每个聚类中心的调和平均值的和作为聚类的目标函数。 由于提升函数的作用使KHM降低了对初始聚类中心敏感程度。 模糊K调和均值聚类(fuzzy K-harmonic means, FKHM)是在KHM基础上引入模糊概念。 本工作在FKCN和FKHM的基础上, 提出了模糊K-Harmonic-Kohonen网络(fuzzy K-Harmonic Kohonen clustering network, FKHKCN)算法。 FKHKCN根据模糊隶属度计算学习速率, 以FKHM的聚类中心为基础计算FKHKCN的聚类中心, 在聚类过程中降低了对初始聚类中心敏感程度, 提高了聚类准确率。

首先分别采用多元散射校正和Savitzky-Golay对茶叶, 肉类和咖啡的FTIR光谱数据进行预处理, 以消除散射影响和滤除噪声, 再用主成分分析(principal component analysis, PCA)压缩光谱数据, 用线性判别分析(linear discriminant analysis, LDA)对茶叶数据进行鉴别信息提取, 最后分别运行FCM, FKCN和FKHKCN对光谱数据聚类分析。 由实验结果表明: 傅里叶变换红外光谱和FKHKCN可以准确快速地鉴别三种数据集的品种。

1 实验部分
1.1 红外光谱数据

该实验共使用了三个光谱数据集。 第一个数据集来自茶叶样本[16], 包含了优质和劣质的乐山竹叶青以及峨眉山毛峰三种茶叶。 该数据集是在室温下利用傅里叶变换红外光谱分析仪采集的96个茶叶样本的光谱数据, 每种茶叶各32个样本, 波数范围设定为4 001~401 cm-1。

第二个数据集来自咖啡样本[17], 它是通过漫反射傅里叶变换红外光谱法采集的56个样本的光谱数据, 其中两种咖啡Robusta和Arabica分别为27个样本和29个样本, 每个光谱包含范围为5 233~12 338 nm的286个变量。

第三个数据集来自肉类样本[17], 包含了鸡肉、 猪肉和火鸡三种类型。 是利用衰减总折光率和傅里叶变换红外光谱采集的60个样本的光谱数据, 每种类型各20个样本。 每个光谱包含448个变量, 范围在5 353~11 123 nm之间。

1.2 模糊K-Harmonic-Kohonen网络算法

步骤一: 初始化过程, 确定类别数k, 测试样本数n和权重指数m0的值, 且满足n> k> 1, +∞ > m0> 1; 初始循环次数值r=1、 最大循环次数值设为rmax, 误差参数为ε ; 初始类中心设置为cj, 0。

步骤二: 计算第r次循环计算时的模糊隶属度值uij, r。

uij, r=∑t=1kdijdit2mr+1-1(1)

式(1)中: mr为第r次循环计算时的权重指数, mr=m0-rΔ m, Δ m=(m0-1)/rmax; uij, r为第r次循环计算时第j个样本隶属于第i类的模糊隶属度值, 其中dij=‖ xi-cj, r-1‖ , xi为第i个样本数据, cj, r-1为第r-1次循环计算时第j类的类中心, dit=‖ xi-ct, r-1‖ , ct, r-1为第r-1次循环计算时第t类的类中心。

步骤三: 计算第r次循环计算时的学习速率α ij, r

αij, r=(uij, r)mr(2)

步骤四: 计算第r次循环计算时的类中心cj, r

cj, r=cj, r-1+∑i=1nαij, r(xi-cj, r-1)∑l=1kαij, rdij2αil, rdil22∑i=1nαij, r∑l=1kαij, rdij2αil, rdil22(3)

式(3)中, dil=‖ xi-cl, r-1‖ , cl, r-1为第r-1次循环计算时第l类的类中心; α il, r为第r次循环计算时的学习速率α il, r=(uil, r )mr, uil, r为第r次循环计算时第l个样本隶属于第i类的模糊隶属度值。

步骤五: r+1后赋值给变量r。

当‖ cj, r-cj, r-1‖ < ε 或者r> rmax则计算终止, 否则从步骤二计算第r次循环计算时的模糊隶属度值uij, r开始重新计算。

2 结果与讨论
2.1 FTIR的预处理

用红外光谱分析仪采集茶叶样本的光谱数据时, 由于实验环境以及茶叶样本之间形状和颗粒大小的差异, 采集到的光谱数据会存在一定的散射影响。 故而采用多元散射校正对光谱数据进行预处理, 以尽可能地减少散射效应的影响。

在使用光谱仪采集咖啡和肉类样本光谱数据时, 实验外界环境的光照条件和光谱仪自身器件原因等因素的影响, 会使得光谱在采集的过程中产生随机噪声。 因此使用Savitzky-Golay来平滑这两个样本数据集的光谱数据, 最大程度上减少噪声影响。

程序设计和数据处理采用软件Matlab2014b。

2.2 FTIR的主成分分析和线性判别分析

使用FTIR-7600型傅里叶红外光谱分析仪采集得到的茶叶样本的红外光谱数据的维数达到1 868维, 需要用PCA对光谱数据的维数进行压缩。 茶叶的傅里叶光谱数据从原始数据的1 868维降至14维, PCA的累计贡献率为99.74%。 PCA处理后的数据重叠严重不利于茶叶样本的准确聚类, 因此需要再使用LDA对降维后茶叶傅里叶红外光谱数据进行特征提取。 茶叶样本的训练集总数为30个, 由每种茶叶样本中随机抽取的10个样本所构成, 剩余的66个样本作为茶叶的测试集。 利用LDA对14维的训练集计算求取LDA的鉴别向量, 然后将测试集样本投影到这些鉴别向量上实现数据空间的变换, 获得投影后的两维光谱数据。

通过漫反射傅里叶变换红外光谱法采集的咖啡样本的维数较高, 为了提高计算机的运行速率, 利用PCA将光谱数据的维数从268维降至10维, PCA的累计贡献率91.12%。

利用衰减全发射(ATR)技术和傅里叶变换红外光谱采集的肉类的光谱数据维数为448维, 通过使用PCA将样本光谱数据的维数降至15维, PCA的累计贡献率为99.55%。

2.3 计算初始聚类中心

FCM的初始聚类中心取自样本数据, 而FKCN和FKHKCN的初始类中心均为FCM聚类收敛后得到的聚类中心。

2.4 FCM, FKCN和FKHKCN的聚类分析

FCM, FKCN和FKHKCN的初始参数设置: (1)茶叶和肉类数据: 权重指数m=2, 类别数c=3, rmax=100, 循环计算最大误差参数设置为ε =0.000 01。 (2)咖啡数据: 权重指数m=4, 类别数c=2, rmax=100, 循环计算最大误差参数设置为ε =0.001。

2.4.1 聚类准确率

对三种FTIR光谱数据上运行FCM, FKCN和FKHKCN聚类算法实施模糊聚类分析, 聚类准确率如表1所示。 FKCN无法对肉类数据集进行聚类分析, FKHKCN的聚类准确率要高于FCM和FKCN的聚类准确率。

表1 FCM, FKCN和FKHKCN的聚类准确率 Table 1 The clustering accuracies of FCM, FKCN and FKHKCN

2.4.2 聚类收敛状况分析

表2显示了FCM, FKCN和FKHKCN的聚类循环迭代次数。 收敛速度和聚类循环计算次数相关, 循环迭代次数越多则聚类收敛速度越慢。 从表2中可以看出, 除了meat数据集外, FKCN的循环迭代次数最少, 而FCM在meat数据集中循环迭代次数最少。 总体而言, FKHKCN的循环迭代次数适中。

表2 FCM, FKCN和FKHKCN的聚类循环迭代次数 Table 2 The numbers of iterations in FCM, FKCN and FKHKCN clustering algorithms

2.4.3 品种判别方法

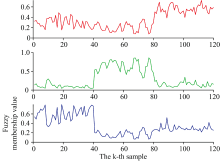
利用以下方法来确定三个数据集中的品种: 首先计算训练样本中不同品种的平均值与测试样本中未知类别的聚类中心之间的欧式距离。 某聚类中心离数据集品种中哪一类的欧式距离最小, 则可以认为该聚类中心所属的类别与该类品种属于同一类别。 鉴别第k个测试样本xk所述类别的方法是: 若样本xk的模糊隶属度uik最大, 则认为xk属于第i类。 图1显示了FKHKCN在肉类数据集的模糊隶属度。

图1 FKHKCN在肉类数据集的模糊隶属度Fig.1 Fuzzy membership value of FKHKCN for meat dataset

3 结论

将模糊K调和聚类和Kohonen聚类网络两种聚类算法结合起来, 提出了模糊K-Harmonic-Kohonen网络(FKHKCN)算法。 FKHKCN对于初始类中心不敏感。 相比于FCM和FKCN, FKHKCN的聚类准确率更高, 循环迭代次数适中。 从实验运行结果来看: 经过光谱预处理, PCA和LDA的维数压缩和特征提取, FKHKCN能够准确地实现三种数据集的品种聚类, 其聚类准确率高, 聚类速度快。

参考文献
[1] Fu H Y, Yin Q B, Xu L, et al. Chemometrics and Intelligent Laboratory Systems, 2016, 157: 43. [本文引用:1]
[2] Dinize P H G D, Barbosa M F, Milanez K D T D, et al. Food Chemistry, 2015, 192: 374. [本文引用:1]
[3] Hu L Q, Yin C L. Food Analytical Methods, 2017, 10: 2281. [本文引用:1]
[4] Cai J X, Wang Y F, Xi X G, et al. International Journal of Biological Macromolecules, 2015, 78: 439. [本文引用:1]
[5] Krahmer A, Bottcher C, Gudi G, et al. Food Chemistry, 2021, 360: 129978. [本文引用:1]
[6] Cebi N, Arici M, Sagdic O, et al. Food Chemistry, 2021, 354: 129495. [本文引用:1]
[7] De Freitas G M, Minho L A C, De Magalhaes B E A, et al. Food Chemistry, 2021, 365: 130477. [本文引用:1]
[8] Ciursa P, Pauliuc D, Dranca F, et al. Food Control, 2021, 130: 108266. [本文引用:1]
[9] Silva K C G, Bourbon A I, Pastrana L, et al. Food Research International, 2021, 141: 110059. [本文引用:1]
[10] Labaky P, Dahdouh L, Sicci J, et al. Journal of Food Engineering, 2021, 300: 110507. [本文引用:1]
[11] Wang Y T, Ren H B, Liang W Y, et al. Journal of Food Engineering, 2021, 311: 110740. [本文引用:1]
[12] Xu Y, Hassan M M, Kutsanedzie F Y H, et al. Quality Assurance and Safety of Crops & Foods, 2018, 10(4): 411. [本文引用:1]
[13] Tahir H E, Zou X B, Li Z H, et al. Food Chemistry, 2017, 226: 202. [本文引用:1]
[14] Wu X H, Wu B, Sun J, et al. Journal of Food Process Engineering, 2017, 40(6): e12355. [本文引用:1]
[15] Zhou Z P, Zhao X X, Zhu S W. Multimedia Tools and Applications, 2018, 77(12): 15139. [本文引用:1]
[16] Wu X H, Zhou J, Wu B, et al. Journal of Food Process Engineering, 2019, 42: e13298. [本文引用:1]
[17] Zheng W, Fu X, Ying Y. Chemometrics and Intelligent Laboratory Systems, 2014, 139: 42. [本文引用:2]