基于色散偏振度的乳化油光谱检测系统研究

引用本文

王晓, 刘木华, 徐将. 基于色散偏振度的乳化油光谱检测系统研究[J]. 光谱学与光谱分析, 2022,42(9): 2689-2693.
WANG Xiao, LIU Mu-hua, XU Jiang. Study on Spectral Detection System of Emulsified Oil Based on the Degree of Dispersion Polarization[J]. Spectroscopy and Spectral Analysis, 2022,42(9): 2689-2693.
Doi:10.3964/j.issn.1000-0593(2022)09-2689-05 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于色散偏振度的乳化油光谱检测系统研究

王晓, 刘木华, 徐将^*

江西农业大学工学院, 江西南昌 330045

*通讯作者 e-mail: xujiangstart@163.com

作者简介: 王晓, 1986年生, 江西农业大学工学院实验师 e-mail: wangxiao0712@sina.com

收稿日期: 2020-06-04 接受日期: 2021-12-23

基金: 国家自然科学基金项目(31271612), 江西省教育厅科技计划项目(GJJ190244)资助

摘要

以色散偏振光谱检测技术为背景, 着重研究了乳化油颗粒的偏振光学特性及米散射物理模型, 构建了色散偏振度光谱检测系统。在400~700 nm波长范围内, 分别对四种样品进行了301个波段的光谱反射率采集。结合贝塞尔函数和汉克尔函数, 推导出了入射光波长与散射光偏振振幅矢量的关系, 提取了一个新的特征参数: 色散偏振度(DODP)。在暗室条件下, 对乳化油样品ND18和ND75进行测量, 利用色散偏振公式计算出了样品在各测量波长处的偏振度值, 验证了基于DODP值检测乳化油的可行性。研究发现, 虽然米散射的解是由单个球体的衍射推导而来, 但是只要它们的直径和组成相同, 且彼此之间的距离比波长大, 也同样可以用于任意数量的球的衍射。在这种情况下, 被不同球体散射的光之间没有相干的相位关系, 总散射能量等于被一个球体散射的能量乘以它们的整数。当观测平面与入射波电矢量振动方向之间的夹角 ϕ=0或者 ϕ=π/2时, 散射光分量Eθ(s)或者Eϕ(s)消失。由于ND18的粒径比ND75的粒径小, 所以ND18的前向散射波瓣较大, 前向散射与后向散射的比值较小。在相同光照条件下, ND75的多次散射现象要比ND18严重。根据路径相关矩阵的理论, 多次散射容易引起退偏振, 二次辐射波会在角域内扩散和分布。因此, 被测乳化油表面产生的散射次数与入射光能的阻尼能力成正比。由于乳化油表面入射光的能量耗散存在差异, 因此能量耗散率与入射波矢量方向的前向散射振幅的分量成正比, 且乳化油的偏振散射程度不同于入射光的偏振散射程度。实验结果表明, DODP可以反映出乳化油由多次色散引起的去偏振能力。由于模拟光源是自然光, 所以计算散射光的偏振参数非常方便, 可以大大缩短数据处理时间, 减小实验误差。 DODP不仅能够识别海水中的乳化油, 而且能够区分不同浓度的污染物, 准确识别出乳化油的边缘扩散。

关键词: 偏振振幅矢量; 乳化油; 色散偏振度; 米散射; 路径相干矩阵

中图分类号:O4 文献标志码:A

Study on Spectral Detection System of Emulsified Oil Based on the Degree of Dispersion Polarization

WANG Xiao, LIU Mu-hua, XU Jiang^*

School of Engineering, Jiangxi Agricultural University, Nanchang 330045, China

*Corresponding author

Abstract

Based on the spectrum detection technology of dispersion polarization, the optical polarization characteristics of emulsified oil particles and the Mie scattering physical model have been emphatically studied, and the spectrum detection system of dispersion polarization degree has been constructed. In the wavelength range of 400-700nm, the spectral reflectance of 301 bands was collected for four samples. Combining the Bessel function and Hankel function, the relationship between the wavelength of incident light and the polarization amplitude vector of the scattered light has been derived, and a new characteristic parameter has been extracted: the degree of dispersion polarization (DODP). Under darkroom conditions, the emulsified oil samples ND18 and ND75 were measured, and the polarization value of the sample at each measurement wavelength was calculated using the dispersion polarization formula, verifying the feasibility of detecting emulsified oil based on DODP value. This study found that although the solution of Mie scattering is derived from the diffraction of a single sphere. As long as their diameter and composition are the same, and the distance between each other is greater than the wavelength, They can also be used to diffract any number of balls. There is no coherent phase relationship between lightly scattered by different spheres, and the total scattered energy is equal to the energy scattered by a sphere multiplied by their integers. When the angle between the observation plane and the vibration direction of the incident wave electric vector is ϕ=0 or ϕ=π/2, the scattered light componentEθ(s) andEϕ(s) disappears. Since the particle size of ND18 is smaller than that of ND75, the forward scattering lobe of ND18 is larger, and the ratio of forwarding scattering to backward scattering is small. Under the same lighting conditions, the multiple scattering of ND75 is more serious than that of ND18. According to the theory of path correlation matrix, multiple scattering is likely to cause depolarization, and secondary radiation waves will spread and distribute in the angular domain. Therefore, the number of scatterings generated on the surface of the emulsified oil measured is proportional to the damping capacity of the incident light energy. Due to the difference in energy dissipation of incident light on the surface of emulsified oil, the energy dissipation rate is proportional to the component of the forward scattering amplitude in the direction of the incident wave vector, and the degree of polarized scattering of emulsified oil is different from the degree of polarized scattering of incident light. Experimental results show that DODP can reflect emulsified oil’s depolarization ability caused by multiple dispersions. Since the simulated light source was natural light, it was very convenient to calculate the polarization parameters of scattered light, which could greatly shorten the data processing time and reduce the experimental error. DODP can identify emulsified oil in seawater and distinguish the concentration of pollutants and accurately identify the edge diffusion of emulsified oil.

Keyword: Polarization amplitude vector; Emulsified oil; Degree of dispersion polarization; Mie scattering; Path coherence matrix

文章图片

引言

海上石油运输在原油贸易中占有重要的地位, 直接影响着全球的经济和人民的生活。近年来, 海上石油运输量急剧上升。油轮等各类船舶密度不断增加, 造成溢油事故频频发生。溢油对海洋环境和海洋生物资源的污染十分严重^[1]。因此, 海洋环境面临着严峻的挑战。在溢油事故发生后, 如何科学、快速地测量溢油面积及分布浓度, 直接关系到海洋溢油污染的有效控制和回收。

在溢油检测的研究中, 遥感卫星为我们提供了宝贵的空间图像数据。例如, 美国国家航空航天局(NASA)新千年计划(NMP)的建立为仪器和航天器技术的飞行提供了有效性验证, 这些技术的提出降低了研究成本, 使得地球观测的新方法成为可能^{[2, 3]}。

谱分析是遥感检测技术中的重要组成部分, 主要的算法有简单的Beer-Lambert定律、经典的最小二乘(CLS)重建^{[4, 5]}、逐步多元线性重建(SMLR)^[6]、偏最小二乘(PLS)回归^[7]和主成分回归(PCR)^[8]。研究发现, 现有的监测方法对海上厚油膜的测量是非常有效的。然而, 这些算法是纯粹的大型数据分析工具, 并不涉及媒介的物理机制。此外, 在光谱测量的研究中, 反射模型的精度还没有满足数据处理的需求^{[9, 10]}, 特别是在溢油检测方面。在海水的强烈运动下, 边缘部分的溢油与海水混合形成乳化油颗粒, 其光学特性比油膜复杂得多, 导致测量精度明显下降。

本文通过研究微颗粒在远场的米散射特性, 将其作为目标识别模型的基础, 推导出了色散偏振度(DODP)。在远场的不同波长上, DODP可以用来描述不同粒子改变入射场内光波偏振特性的能力。此外, 还测定了不同粒径乳化油样品的光谱数据。大量实验结果证明, DODP模型可以作为海上乳化油识别监测的基础, 并且可以较好地反演出乳化油的浓度。

1 米散射测量

米散射理论是单色平面光照下均匀介质中均匀粒子麦克斯韦方程的严格数学解。根据这一理论, 可以得到在距离观测点r处的散射强度为

$I_{sca} = I_{0} (\frac{λ^{2}}{8 π^{2} r^{2}}) [| s_{1} (β) |^{2} si n^{2} φ + | s_{2} (β) |^{2} co s^{2} φ]$ (1)

式(1)中, λ 为入射光的波长, I₀为入射光的强度, I_sca为散射光的强度, β 为散射角, φ 是偏振光的偏振角。并且

$\begin{array}{l} s_{1} (β) = \overset{\infty}{\sum_{n}} \frac{2 n + 1}{n (n + 1)} [a_{n} π_{n} + b_{n} τ_{n}] \\ s_{2} (β) = \overset{\infty}{\sum_{n}} \frac{2 n + 1}{n (n + 1)} [a_{n} τ_{n} + b_{n} π_{n}] \end{array}$ (2)

式(2)中, s₁(β )和s₂(β )都为振幅函数, a_n和b_n分别是与贝塞尔函数和汉克尔函数有关的参量。 π _n和τ _n是与勒让德函数相关的物理量, 只与散射角β 有关。这几种函数之间的关系式可以表示为

$\begin{array}{l} a_{n} = \frac{φ_{n} (q) φ'_{n} (\dot{n} q) - \dot{n} φ'_{n} (q) φ_{n} (\dot{n} q)}{ε_{n} (q) φ_{n}^{'} (\dot{n} q) - \dot{n} ε'_{n} (q) φ_{n} (\dot{n} q)} \\ b_{n} = \frac{\dot{n} φ_{n} (q) φ'_{n} (\dot{n} q) - φ'_{n} (q) φ_{n} (\dot{n} q)}{\dot{n} ε_{n} (q) φ'_{n} (\dot{n} q) - ε_{n}^{'} (q) φ_{n} (\dot{n} q)} \end{array}$ (3)

式(3)中, φ _n(q)是贝塞尔函数, ε _n(q)是第一类汉克尔函数。 φ '_n(q)和ε '_n(q)分别是φ _n(q)和ε _n(q)的一阶导数。 q是一个不稳定的维度, 且q=π D/λ 。 D是粒子的实际直径, $\dot{n}$ 是散射粒子相对于周围介质的折射率。它是一个复数, 虚部表示粒子对光能量吸收的量化。

实验分别对两种乳化油样品进行了米散射测量。在30° 散射角下观察了样品表面反射率与入射光波长的关系。同时, 还对海水的瑞利散射特征进行了分析。在400~700 nm波长范围内, 301个波段的光谱反射率如图1所示。

	Figure Option View Download New Window
	图1 入射光反射率与波长的关系Fig.1 The relationship between reflectance and wavelength of incident light

为了获得稳定的实验数据, 在实验中对每个样品进行了5次信号采集, 然后对数据进行平均, 得到样品的光谱反射率。 ND75是由75%的原油和25%的海水组成的乳化油。 ND18由18%的原油和82%的海水组成。 SWB是标准的白板, 用来修正实验数据。在400~525 nm波段范围内, 乳化油和海水的反射率非常接近, 无法区分。在525~700 nm波段范围内, 海水和乳化油的反射率差异也不明显, 很难区分。在整个测量范围内, 乳化油和海水的反射率值基本相同。由此可见, 在可见光测量范围内, 仅依靠散射强度信息是无法识别出海水中的乳化油污染物的。因此, 急需一种更加有效、快速的方法来实现对海洋乳化油的鉴定和监测。

2 实验部分

2.1 装置与方法

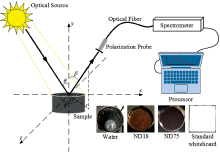
为了防止背景光对测量数据的影响, 对不同浓度乳化油样品的DODP模型试验在暗室中进行。光源为模拟太阳光的卤素灯, 入射角为90° 。探测器为分析光谱仪(FieldSpec 4 350~2 500 nm), 用于测量米散射的光谱数据, 偏振探头的视角为30° 。

如图2所示, 卤素灯发出的平行光垂直照射于样品表面。根据米散射原理, 在散射角方向, 通过光纤和偏振探针, 由光谱仪获得散射光信号。在采集偏振信息之前, 用标准白板对光谱测量环境进行校正, 然后采集5次样品信息, 进行平均处理。利用处理器的MATLAB软件对测量数据和偏振参数进行分析。应用色散偏振公式计算样品在各测量波长的偏振度。结合量子力学和波粒二象性, 对分子群样品和晶体结构进行了科学分析, 准确计算出DODP值。由于模拟光源是自然光, 所以其斯托克斯矢量较为简单, 计算散射光的偏振参数非常方便, 可以大大缩短数据处理时间, 减小实验误差。

	Figure Option View Download New Window
	图2 测量示意图Fig.2 The sketch map of measurement

2.2 光波传播路径

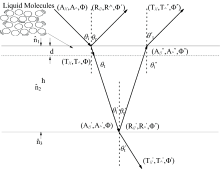
当入射光照射到液体表面时, 用偏振探针收集米散射偏振光。如图3所示, 阳光(A_∥, A_⊥, Φ )照射到石油表面时, 其厚度和复折射率分别为h和 ${\dot{n}}_{2}$ , 乳化油分子群的粒径为d。当光线穿过颗粒时, 产生米散射偏振光(R_∥, R_⊥, Φ ')和折射偏振光(T_∥, T_⊥, Φ )。根据光的弹性理论和麦克斯韦关系(n= $\sqrt[]{ε}$ ), 可以推导出

$\begin{array}{l} T_{∥} = \frac{2 n_{1} \cos θ_{i}}{n_{2} \cos θ_{i} + n_{1} \cos θ_{t}} A_{∥} \\ T_{⊥} = \frac{2 n_{1} \cos θ_{i}}{n_{1} \cos θ_{i} + n_{2} \cos θ_{t}} A_{⊥} \end{array}$ (4a)

$\begin{array}{l} \begin{array}{l} R_{∥} = \frac{n_{2} \cos θ_{i} - n_{1} \cos θ_{t}}{n_{2} \cos θ_{i} + n_{1} \cos θ_{t}} A_{∥}, \\ R_{⊥} = \frac{n_{1} \cos θ_{i} + n_{2} \cos θ_{t}}{n_{1} \cos θ_{i} + n_{2} \cos θ_{t}} A_{⊥} \end{array} \end{array}$ (4b)

	Figure Option View Download New Window
	图3 单一乳化油粒子的偏振散射理论Fig.3 Polarization scattering theory of single emulsion oil particle

将折射定律代入式(4a)和式(4b), 得到

$\begin{array}{l} T_{∥} = \frac{2 \sin θ_{t} \cos θ_{i}}{\sin (θ_{i} + θ_{t}) \cos (θ_{i} - θ_{t})} A_{∥} \\ T_{⊥} = \frac{2 \sin θ_{t} \cos θ_{i}}{\sin (θ_{i} + θ_{t})} A_{⊥} \end{array}$ (5a)

$\begin{array}{l} \begin{array}{l} R_{∥} = \frac{\tan (θ_{i} - θ_{t})}{\tan (θ_{i} + θ_{t})} A_{∥} \\ R_{⊥} = - \frac{\sin (θ_{i} - θ_{t})}{\sin (θ_{i} + θ_{t})} A_{⊥} \end{array} \end{array}$ (5b)

因为θ _i和θ _t都是实数, 所以式(5a)和式(5b)等式右边的三角因子也是实数。因此, 反射波或透射波的每个分量的相位要么等于入射波对应分量的相位, 要么相差π 。由于T_∥和T_⊥具有与A_∥和A_⊥相同的符号, 所以发射波的相位实际上等于入射波的相位。然而, 在反射波的情况下, 相位将取决于θ _i和θ _t的相对大小。在本次研究中, 第二种介质(油膜)比第一种介质(空气)在光学特征上要更为致密, 即θ _i> θ _t。根据式(4b), R_⊥和A_⊥的符号不同, 因此相位相差π 。同样, R_∥和A_∥的相位也相差π 。

2.3 色散偏振理论

研究发现: 虽然米散射的解是由单个球体的衍射推导出来的, 但是也适用于任意数量的球的衍射。只要它们的直径和组成相同, 且是随机分布的, 彼此之间的距离比波长大。在这种情况下, 被不同球体散射的光之间没有相干的相位关系, 总散射能量等于被一个球体散射的能量乘以它们的整数。因此, 在远场(r≫λ )中, 散射光偏振分量的光强可以表示为

$\begin{array}{l} I_{∥}^{(s)} = \\ \frac{λ^{(Ι) 2}}{4 π^{2} r^{2}} {|\overset{\infty}{\sum_{l}} {(- i)}^{l} [^{e} B_{l} P_{l}^{(1)'} (\cos θ) \sin θ -^{m} B_{l} \frac{P_{l}^{(1)} (\cos θ)}{\sin θ}]|}^{2} \\ I_{⊥}^{(s)} = \\ \frac{λ^{(Ι) 2}}{4 π^{2} r^{2}} {|\overset{\infty}{\sum_{l}} {(- i)}^{l} [^{e} B_{l} \frac{P_{l}^{(1)} (\cos θ)}{\sin θ} -^{m} B_{l} P_{l}^{(1)'} (\cos θ) \sin θ]|}^{2} \end{array}$ (6)

式(6)中, k是波数的平方(球面内实外复)。球体周围介质的量用上标Ⅰ 标记, 球体的量用上标Ⅱ 标记。 l是电波系列。 θ 是入射光传播的方向。

系数^eB_l和^mB_l的表达式如式(7)所示

$\begin{array}{l} ^{e} B_{l} = i^{l + 1} \frac{2 l + 1}{l (l + 1)} \frac{\dot{n} Ψ'_{l} (q) Ψ_{l} (\dot{n} q) - Ψ_{l} (q) Ψ'_{l} (\dot{n} q)}{\dot{n} ζ_{l}^{(1)'} (q) Ψ_{l} (\dot{n} q) - ζ_{l}^{(1)} (q) Ψ'_{l} (\dot{n} q)} \\ ^{m} B_{l} = i^{l + 1} \frac{2 l + 1}{l (l + 1)} \frac{\dot{n} Ψ_{l} (q) Ψ'_{l} (\dot{n} q) - Ψ'_{l} (q) Ψ_{l} (\dot{n} q)}{\dot{n} ζ_{l}^{(1)} (q) Ψ'_{l} (\dot{n} q) - ζ_{l}^{(1)'} (q) Ψ_{l} (\dot{n} q)} \end{array}$ (7)

在式(7)中

$\begin{array}{l} ζ_{l}^{(1)} (q) = Ψ_{l} (q) - i χ_{l} (q) = \sqrt[]{\frac{πq}{2}} ε_{l + 1 / 2} (q) \\ Ψ_{l} (q) = \sqrt[]{\frac{πq}{2}} φ_{l + 1 / 2} (q) \\ χ_{l} (q) = - \sqrt[]{\frac{πq}{2}} N_{l + 1 / 2} (q) \end{array}$ (8)

式(8)中, N_l₊₁_/₂(q)是纽曼常数。

此时, 勒让德多项式可以改写成

$P_{l}^{(1)} (\cos θ) = \frac{l}{\sin θ} [P_{l - 1} (\cos θ) - \cos θ P_{l} (\cos θ)]$ (9)

在远离球体处(r≫λ ), 它可以近似地表示为

$\begin{array}{l} P_{l}^{(1)} (\cos θ) = \sin θ \\ P_{l}^{(1)'} (\cos θ) \sin θ = - \cos θ \end{array}$ (10)

因此, 观测平面(由入射光传播方向和观测方向组成的平面)上的波电场矢量可以表示为

$\begin{array}{l} | E_{θ}^{(s)} |^{2} = I_{∥}^{(s)} co s^{2} ϕ \\ | E_{ϕ}^{(s)} |^{2} = I_{⊥}^{(s)} si n^{2} ϕ \end{array}$ (11)

式(11)中, ϕ 为该平面与入射波电矢量振动方向之间的夹角。根据式(11)可知, 当ϕ =0或者ϕ =π /2时, 散射光分量 $E_{θ}^{(s)}$ 或者 $E_{ϕ}^{(s)}$ 消失。所以当观察平面平行或垂直于主振动时, 散射光是线偏振的。对于任何其他方向(θ , ϕ ), 光通常是椭圆偏振的, 因此比率 $E_{θ}^{(s)}$ / $E_{ϕ}^{(s)}$ 是复杂的。

3 结果与讨论

一般来说, 自然界中的入射光是自然光, 因此散射光是部分偏振的, 并且 $I_{∥}^{(s)}$ 和 $I_{⊥}^{(s)}$ 都不为零。可以把散射光的偏振度(Dop)定义为

$Dop = |\frac{I_{⊥}^{(s)} - I_{∥}^{(s)}}{I_{⊥}^{(s)} + I_{∥}^{(s)}}|$ (12)

但是, 式(12)是对均匀光的讨论。本次研究将分析不同波长处散射偏振光的变化。当光通过介质时, 其频率不会改变, 因此可以得到

$\begin{array}{l} \dot{n} = \frac{c}{v} = \frac{c}{ωλ} = \frac{c}{ω} \frac{1}{λ} \\ \dot{n} q = \frac{c}{ω} \frac{1}{λ} \frac{πD}{λ} = \frac{πcD}{ω} \frac{1}{λ^{2}} \end{array}$ (13)

式(13)中, c是光在真空中的传播速度, ω 是光在介质中的传播频率。通过公式推导, 发现在偏振度方程中, 只有系数^eB_l和^mB_l的表达式和波长有关。因此, 将色散偏振度(DODP)定义为

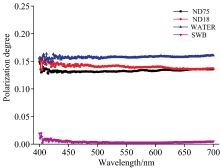
DODP(λ )= $\frac{{|\overset{\infty}{\sum_{l}} [^{e} B_{l} +^{m} B_{l} \cos θ]|}^{2} - {|\overset{\infty}{\sum_{l}} [^{e} B_{l} \cos θ +^{m} B_{l}]|}^{2}}{{|\overset{\infty}{\sum_{l}} [^{e} B_{l} +^{m} B_{l} \cos θ]|}^{2} + {|\overset{\infty}{\sum_{l}} [^{e} B_{l} \cos θ +^{m} B_{l}]|}^{2}}$ (14)

在相同的实验条件下, 对两种乳化油样品进行了DODP的测量实验。实验光谱数据如图4所示。

	Figure Option View Download New Window
	图4 不同波长处的DODP趋势图Fig.4 Trend of DODP at different wavelengths

图4中, 粉色三角形点是标准白板的DODP。因为标准白板是朗伯函数, 可见光带中的测量值几乎都为零。红色圆点为ND18的DODP, 黑色正方形为ND75的测量值。在测量过程中, 由于ND18的粒径比ND75的粒径小, 所以ND18的前向散射与后向散射的比值更小, 前向散射波瓣更大。在相同光照条件下, ND75的多次散射比ND18严重。根据路径相干矩阵理论, 多次散射容易引起退偏振, 二次辐射波会在角域内扩散和分布。被测介质表面产生的散射次数与入射光能的阻尼能力成正比^{[11, 12]}。根据光电效应, 乳化油表面入射光的能量耗散存在差异。当光照条件相同时, 能量耗散率与入射波矢量方向的前向散射振幅的分量成正比。因此, 乳化油的偏振散射程度不同于入射光的偏振散射程度。 DODP反映了乳化油由多次色散引起的去偏振能力。可作为区分不同浓度、不同粒径乳化油的重要参数。

蓝色三角点是海水的斑点。海水的粒径很小, 散射效应可视为瑞利散射, DODP公式可进一步简化为

$DOD P_{(Rayleighscattering)} = \frac{si n^{2} θ}{1 + co s^{2} θ}$ (15)

由此可见, 海水的DODP只与散射光的传播方向有关。在本次测量条件下, 它们具有固定的值。在可见光范围内, DODP可用于区分乳化油和海水, 且效果明显。图4中的DODP可用于监测海上乳化油的污染情况, 并能够准确地反映出乳化油的污染程度, 这一优势弥补了传统的光学检测技术的不足。

4 结论

建立了乳化油偏振光学检测技术的分析方法, 并通过测量不同波长下米散射光的偏振状态, 验证了被测乳化油样品的偏振特性。将偏振光分为三部分, 分别考虑分子间的路径。结合贝塞尔函数和汉克尔函数, 推导出了米散射光偏振振幅矢量与入射光波长的关系。最后, 通过实际乳化油样品的测量对检测系统进行了验证, 利用MATLAB软件计算出了色散偏振度。结果表明, DODP可以快速高效地对海水中的乳化油进行鉴别, 同时也可用于检测不同浓度的乳化油污染物。该光谱测量技术准确、高效, 适合于海面溢油的识别和评价。

参考文献

文献列表

[1]	Kessler J D, Valentine D L, Redmond M C, et al. Science, 2011, 331(6015): 312. [本文引用:1]
[2]	LU Ying-cheng, HU Chuan-min, SUN Shao-jie, et al(陆应城, 胡传民, 孙绍杰, 等). Journal of Remote Sensing(遥感学报), 2016, 20(5): 1259. [本文引用:1]
[3]	Lu Y, Zheng G, Tian Q, et al. Applied Optics, 2013, 52(4): 879. [本文引用:1]
[4]	Schleusener J, Carrer V, Patzelt A, et al. Quantum Electronics, 2019, 49(1): 6. [本文引用:1]
[5]	Ferreira A R, Fernand es L F S, Cortes R M, et al. Science of Total Environment, 2017, 583: 466. [本文引用:1]
[6]	Li Y, Liu S, Liao Z, et al. Canadian Journal of Soil Science, 2012, 92(6): 845. [本文引用:1]
[7]	Hecker C, Dilles J H, Meijde M V D, et al. Geochemistry, Geophysics, Geosystems, 2012, 13(3): 3021. [本文引用:1]
[8]	Junttila V, Laine M. Remote Sensing of Environment, 2017, 192: 45. [本文引用:1]
[9]	Xu J, Qian W, Lu D, et al. Infrared Physics & Technology, 2016, 77: 474. [本文引用:1]
[10]	Lu Y, Li X, Tian Q, et al. Optics Express, 2012, 20(22): 24496. [本文引用:1]
[11]	Qian W, Zhou X, Lu Y, et al. Optics Letters, 2015, 40(18): 4336. [本文引用:1]
[12]	XU Jiang, QIAN Wei-xian, LU Dong-ming, et al(徐将, 钱惟贤, 路东明, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(1): 183. [本文引用:1]

2011

0.0

... 溢油对海洋环境和海洋生物资源的污染十分严重^[1] ...

2016

0.0

... 例如, 美国国家航空航天局(NASA)新千年计划(NMP)的建立为仪器和航天器技术的飞行提供了有效性验证, 这些技术的提出降低了研究成本, 使得地球观测的新方法成为可能^[2,3] ...

2013

0.0

2019

0.0

... 谱分析是遥感检测技术中的重要组成部分, 主要的算法有简单的Beer-Lambert定律、经典的最小二乘(CLS)重建^[4,5]、逐步多元线性重建(SMLR)^[6]、偏最小二乘(PLS)回归^[7]和主成分回归(PCR)^[8] ...

2017

0.0

2012

0.0

2012

0.0

2017

0.0

2016

0.0

... 此外, 在光谱测量的研究中, 反射模型的精度还没有满足数据处理的需求^[9,10], 特别是在溢油检测方面 ...

2012

0.0

... 此外, 在光谱测量的研究中, 反射模型的精度还没有满足数据处理的需求^[9,10], 特别是在溢油检测方面 ...

2015

0.0

... 被测介质表面产生的散射次数与入射光能的阻尼能力成正比^[11,12] ...

2017

0.0

... 被测介质表面产生的散射次数与入射光能的阻尼能力成正比^[11,12] ...