推扫式多挡增益光谱成像模拟及噪声分析

引用本文

金鹏飞, 汤瑜瑜, 危峻. 推扫式多挡增益光谱成像模拟及噪声分析[J]. 光谱学与光谱分析, 2022,42(6): 1922-1927.
JIN Peng-fei, TANG Yu-yu, WEI Jun. Simulation and Noise Analysis of Pushbroom Multi-Gain Spectral Imaging[J]. Spectroscopy and Spectral Analysis, 2022,42(6): 1922-1927.
Doi:10.3964/j.issn.1000-0593(2022)06-1922-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

推扫式多挡增益光谱成像模拟及噪声分析

金鹏飞^1,^2,³, 汤瑜瑜^2,^3,^*, 危峻^2,³

1.中国科学院大学, 北京 100101

2.中国科学院上海技术物理研究所, 上海 200083

3.中国科学院红外探测与成像技术重点实验室, 上海 200083

*通讯作者 e-mail: tangyuyu@mail.sitp.ac.cn

作者简介: 金鹏飞, 1994年生,中国科学院上海技术物理研究所博士研究生 e-mail: j_peng_fei@163.com

收稿日期: 2021-04-22 修回日期: 2021-06-11

基金: 国家自然科学基金项目(11573049)资助

摘要

综合性遥感监测对载荷的灵敏度和动态范围都有较高的要求, 为此提出一种基于逐像元多挡增益切换的光谱成像方法。不同于帧增益或者行列增益切换的成像方式, 该方法利用4T-APS CMOS探测器无破坏读出的特点, 可以进行像元级的增益优化。这种方式可以兼顾水体、植被、云层等多要素的成像需求, 极大地提高了载荷的研制效益。其基本原理为探测器先进行全局曝光, 然后根据多级积分电容的饱和判断, 选取不饱和的最高增益信号以增益码加信号的形式下传。地面根据增益码对应的定标系数反推出像元真实辐射值。由于谱段多且为分段响应, 为保证系统的定量化应用, 建立多挡增益光谱成像模型并进行噪声分析具有重要意义。通过对噪声类型的分析, 建立了多挡增益下的泊松-高斯噪声模型。基于该模型计算了像元受噪声影响以低增益读出的概率。结果表明, 虽然噪声会影响读出增益的变化, 但影响区间极小, 入瞳辐亮度在5 mW·cm^-2·μm^-1·sr^-1以内, 信号比增益挡位辐亮度分界值小0.05 mW·cm^-2·μm^-1·sr^-1即可保证正常读出的概率大于99.6%。随着信号增强, 光子噪声增大, 增益减小, 影响区间扩大。根据多挡增益信噪比模型, 分析得出光谱模式与合并通道模式下的信噪比变化。最后, 利用宽波段成像光谱仪(WIS)数据作为入瞳辐亮度进行了四挡增益的推扫式光谱成像模拟, 分析了多挡增益光谱图像的固有特点。根据噪声模型对中心波长为0.443 μm的光谱图像添加1~3 σ的随机噪声, 分析了噪声对地物目标所处增益的影响。结果显示, 在满足信噪比指标的前提下, 该系统的单挡动态范围为74 dB, 总动态范围可达114 dB。该方法不但提高了水体等弱信号的信噪比, 而且可以保证建筑、云层等亮目标不饱和。成像模拟及噪声分析不仅有利于该载荷的后续研制, 也可以为同类光谱仪器的设计提供参考。

关键词: 遥感; 推扫式光谱成像; 逐像元; 多挡增益; 系统仿真

中图分类号:TH744 文献标志码:A

Simulation and Noise Analysis of Pushbroom Multi-Gain Spectral Imaging

JIN Peng-fei^1,^2,³, TANG Yu-yu^2,^3,^*, WEI Jun^2,³

1. University of Chinese Academy of Sciences, Beijing 100101, China

2. Shanghai Institute of Technical Physics, Chinese Academy of Sciences, Shanghai 200083, China

3. Key Laboratory of Infrared System Detection and Imaging Technology, Chinese Academy of Sciences, Shanghai 200083, China

*Corresponding author

Abstract

Comprehensive remote sensing monitoring requires high sensitivity and dynamic range of the sensor, so a spectral imaging method based on a pixel by pixel gain switching is proposed. Unlike from the frame gain or row column gain switching imaging methods, this method can optimize the gain at pixel level by using the nondestructive readout characteristics of the 4T-APS CMOS detector. This method can take into account the imaging needs of water, vegetation, cloud and other factors and greatly improve the development efficiency of the payload. The basic principle is that the detector firstly carries out global exposure and then according to the saturation judgment of the multi-stage integral capacitance, selects the unsaturated highest gain signal to be transmitted down in the form of gain code plus signal. The real radiation value of the pixel is derived from the calibration coefficient of the gain code. Due to the multi spectral segment and piecewise response, it is important to establish the multi-gain spectral imaging model and analyze the noise to ensure the system's quantitative application. Based on the analysis of noise types, the Poisson Gaussian noise model with multi-gain is established. Based on the model, the probability of low gain readout is calculated. The results show that although the noise will affect the change of the readout gain, the influence range is very small. When the radiance is within 5 mW·cm^-2·μm^-1·sr^-1, the signal is less 0.05 mW·cm^-2·μm^-1·sr^-1 than the value of the gain gear, so the probability of normal readout is greater than 99.6%. With the enhancement of the signal, the photon noise increases, the gain decreases, and the influence range expand. According to the multi-gain SNR model, the changes of SNR in spectral mode and combined channel mode are analyzed. Finally, the push broom spectral imaging simulation of four gains is carried out using the wideband imaging spectrometer (WIS) data as the entrance pupil radiance, and the inherent characteristics of the multi-gain spectral image are analyzed. Based on the noise model, add 1~3 σ random noise to the spectral image with center wavelength of 0.443 μm, the influence of the noise on the gain of ground objects is analyzed. The results show that on the premise of meeting the SNR index, the single gain dynamic range of the system is 74 dB, and the total dynamic range is 114 dB. This method improves the SNR of weak signals such as water and ensures the unsaturation of bright targets such as buildings and clouds. Imaging simulation and noise analysis are conducive to the subsequent development of the sensors and provide a reference for the design of similar spectral instruments.

Keyword: Remote sensing; Pushbroom spectral imaging; Pixel by pixel; Multi-gain; System simulation

文章图片

引言

自20世纪80年代美国喷气推进实验室(JPL)研制出第一台机载成像光谱仪, 光谱成像技术开始在遥感领域得到大量应用^[1]。光谱成像系统组成较为复杂, 定量化要求高。针对不同的搭载平台、监测目标、成像方式, 研制前的模拟仿真和研制后的定标校准具有重要意义。尤其是对于一种全新的系统结构或者成像方式, 仿真实验可以给系统搭建调试提供有力的参考。例如王建宇等根据地物目标的辐射特性和系统灵敏度方程, 分析了高光谱成像系统中的各种噪声来源, 建立了空域、时域等多种噪声模型, 谱段范围包括可见光到热红外, 具有一定的普适性^[2]; 余达等将超高速电子倍增技术和成像光谱技术相结合, 构建了基于电子倍增的成像链模型, 并利用LOWTRAN7软件进行模拟仿真, 计算出该成像系统不同条件下的SNR, 从而选择适当的电子倍增增益^[3]。

推扫式成像光谱仪是航天遥感载荷的常见类型, 例如欧空局的海陆颜色仪(OLCI), 我国天宫二号上搭载的宽波段成像光谱仪(WIS)。由于地面目标类型复杂, 综合性的遥感监测对载荷的灵敏度和动态范围都有较高的要求。但是对于单帧成像, 信噪比与动态范围为相互制约的关系。目前常见的解决方法为部分波段或者全谱段设置2~3挡增益, 通过地面指令切换每一帧图像的增益, 或者获取所有增益的数据。例如美国S-NPP卫星上搭载的可见光红外成像辐射仪(VIIRS)设置有DNB通道, 为满足成像需求, 利用三挡增益同时获取目标信号, 对应的辐射增益为119 000:477:1^[4]。显然, 目前的方法一方面会导致数据量激增, 另一方面只能做到帧切换, 无法实现单帧内各像元的高灵敏度大动态范围信号获取。本文提出一种基于逐像元多挡增益切换的光谱成像方法, 可以较好地解决以上矛盾。同时建立相应的成像噪声模型, 并利用已有遥感数据完成系统成像模拟。

1 基本原理

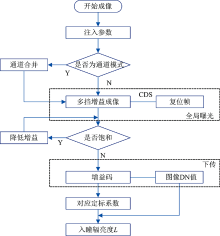
成像光谱仪主要由前端光学系统、分光组件、探测器以及电子学系统组成。推扫式是结合面阵探测器的固体扫描和搭载平台的前进运动完成二维扫描, 即一维进行空间成像, 另一维完成光谱的扫描。由于成像系统与地面之间存在高速运动, 多次曝光^[5]、光强调制^[6]等常见的动态范围拓展方法无法适用^[7]。考虑到推扫式光谱成像的特点, 一次曝光多次信号采集是提高灵敏度和动态范围的可行途径。逐像元多挡增益光谱成像方法的本质即利用4T-APS CMOS探测器无破坏读出的特点进行多次信号采集, 选取不饱和的最高增益信号进行下传, 最后地面根据该增益挡位对应的定标系数反推出真实的入瞳辐射。该方法的成像流程如图1所示。

	Figure Option View Download New Window
	图1 基于逐像元多挡增益的光谱成像流程图Fig.1 Flow chart of spectral imaging based on pixel by pixel multiple-gain

虽然该方法不但解决了多挡增益成像数据量大的问题, 而且极大地提高了系统灵敏度和动态范围, 但是也会带来增益跳变、线性度差等问题。在增益挡位衔接处必然会有一定概率出现跳变, 即高增益下的强信号变成低增益下的弱信号输出。因此, 针对该方法建立相应的系统噪声模型并进行成像模拟十分必要。

2 系统成像模型及噪声分析

2.1 成像模型

假设系统选用的探测器为光子探测器, 那么可以根据量子效率计算出像元信号电子数, 即

$N_{s} (λ) = \frac{A_{d} T_{int}}{4 F^{2} hc} \int_{λ_{1}}^{λ_{2}} π L (λ) τ_{0} (λ) η (λ) λ d λ$ (1)

式(1)中: F为光学系统F数, A_d为像元面积, T_int为积分时间, L(λ)为入瞳辐亮度, τ ₀(λ)和η (λ)分别表示系统光学效率和探测器量子效率。某挡增益对应的积分电容为C_int(i), 转换增益为G_conv(i), 产生的信号电压为

$V_{S} (λ, i) = \frac{N_{s} (λ) q}{C_{int} (i)} = G_{conv} (i) N_{s} (λ)$ (2)

信号电压V_S(λ, i)必然处于探测器工艺所限制的电压摆幅内

$V_{out} (λ, i) = \max (V_{noise} (λ), \min (V_{S} (λ, i), V_{\max} (λ)))$ (3)

对于目前主流CMOS工艺来说, V_max(λ)为1~2 V, 噪声电压V_noise(λ)为150~250 μV。从这里可以看出, 单增益成像受探测器工艺影响, 输出电压的动态范围极限为82 dB。对应ADC的选择需要考虑动态范围的匹配, 14 bit量化位数的ADC的动态范围为84 dB, 可以满足需求。因此, 某一增益挡位输出的图像DN值为

$D N_{S} (λ, i) = 2^{n} \frac{V_{out} (λ, i)}{V_{ref}}$ (4)

若 $D N_{S} (λ, i) \leq D N_{threshold}$ , 可以认为在第i挡增益下未饱和, 否则切换更小增益挡位进行成像。 $D N_{threshold}$ 的理论值为 $2^{n} - 1, n$ 为所选ADC的量化位数, 但实际情况还需根据电子学调试来决定。

2.2 噪声模型

模拟成像链路的另一组成部分为噪声, 这也是影响系统性能的重要因素。成像光谱仪的噪声包括时域噪声和空域噪声两部分。时域噪声跟每个像元自身相关, 主要包括暗电流噪声、信号涨落引起的量子噪声、热噪声等。影响单个像元信号及增益的主要为时域噪声, 这里不对空间噪声进行分析。如表1所示, 根据是否与曝光量相关, 可以将成像链路中的时域噪声分为两类^[8]。

表1 时域噪声与曝光量的关系 Table 1 Relationship between time domain noise and exposure

噪声类型		与曝光量的关系
时域噪声	量子噪声	∝ $\sqrt[]{\exp}$
时域噪声	读出噪声	无关(加性)

表1 时域噪声与曝光量的关系 Table 1 Relationship between time domain noise and exposure

其中量子噪声可近似用泊松分布描述的散粒噪声来表示。读出噪声近似为高斯分布的白噪声。假设泊松分布的均值为μ_j, j表示第j行光谱数据, 高斯分布的均值为0, 标准差为σ _i, 那么混合泊松-高斯分布的概率密度函数为^[9]

$f (x) = \overset{\infty}{\sum_{k = 0}} \frac{μ_{j}^{k}}{k!} e^{- μ_{j}} \frac{1}{\sqrt[]{2 π} σ_{i}} e^{- {(x - k)}^{2} / (2 σ_{i}^{2})}$ (5)

式(5)中, x为像元取值, 标准差σ _i取决于增益挡位。泊松-高斯模型对应的均值为μ_j, 方差为μ_j+ $σ_{i}^{2}$ 。假定μ_j为该像元不受泊松-高斯噪声影响的初始值, 当μ_j≤ DN_threshold时可以认为像元值在该增益下不饱和。那么, 像元值受噪声影响以更低增益读出的概率为

$\begin{array}{l} P (x > D N_{threshold}) = \\ \int_{D}^{N_{threshold}} \overset{\infty}{\sum_{k = 0}} \frac{μ_{j}^{k}}{k!} e^{- μ_{j}} \frac{1}{\sqrt[]{2 π} σ_{i}} e^{- {(x - k)}^{2} / (2 σ_{i}^{2})} d x \end{array}$ (6)

CMOS探测器直接输出每一行的数字值, 通道模式信号由FPGA片外进行数字合并, 然后饱和判断。通道模式下第i挡增益输出信号为

$DN {(λ, i)}_{channel} = \frac{\overset{n}{\sum_{j = m}} D N_{spec} {(λ, i)}_{j}}{n - m + 1}$ (7)

DN(λ, i)_channel在物理意义上所对应的是m~n连续谱段的中心波长辐亮度。假设合并通道下的每一个光谱行输出数据相互独立, 且数学期望和方差均为有限值, 那么在合并行数较多的情况下, 根据Lyapunov中心极限定理, 合并通道模式信号近似服从正态分布

$DN {(λ, i)}_{channel} ~ N (\frac{\overset{n}{\sum_{j = m}} μ_{j}}{n - m + 1}, \frac{\overset{n}{\sum_{j = m}} μ_{j} + σ_{i}^{2}}{{(n - m + 1)}^{2}})$ (8)

如果光子通量足够大, 离散泊松分布可认为接近连续的高斯分布。那么, 可将光谱模式信号的泊松-高斯模型简化为两个高斯分布的叠加

$D N_{spectrum} (λ, i) ~N (μ_{j}, μ_{j} + σ_{i}^{2})$ (9)

显然, 通道模式下信号标准差近似为光谱模式下的1/ $\sqrt[]{n - m + 1}$ 。通道合并滤去部分噪声, 减少跨挡读出的概率。设f(μ_j, σ _i, x)为高斯分布概率密度函数, 其中σ _i是随μ_j变化的常数值。因此, 大小为μ_j的信号跨挡位以更低增益读出的概率

$f (μ_{j}) = \int_{D}^{N_{threshold}} f (μ_{j}, σ_{i}, x) d x$ (10)

当信号大小处于每挡增益分界点时, 取得理论最大值, 极限概率为1/2。以入瞳辐亮度L为输入变量, μ_j为L在对应增益下的数字信号值。根据上述公式, 易得像元受噪声影响以较低增益读出的概率曲线图。

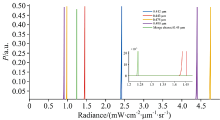
如图2所示, 以中心波长为0.412, 0.443, 0.475和0.49 μm, 带宽为2.16 nm光谱数据和中心波长为0.45 μm、带宽为70 nm的合并通道数据为例进行仿真。可以看出, 由于光学及量子效率的不同, 0.49和0.475 μm的光谱通道在辐亮度为5 mW· cm^-2· μm^-1· sr^-1以内时需要两挡增益读出, 而其余通道只需一挡增益即可满足读出需求。虽然高增益挡位信号以低增益读出的概率会在临界点急剧升高, 但影响区间极小。入瞳辐亮度在5 mW· cm^-2· μm^-1· sr^-1以内时, 信号处于临界点外0.05 mW· cm^-2· μm^-1· sr^-1即可保证正常读出的概率大于99.6%。随着入瞳辐亮度的增大, 光子噪声增大, 影响区间也会增大。由于合并通道压缩了部分噪声, 数据变异程度较小, 相应的影响区间也较小。

	Figure Option View Download New Window
	图2 像元受噪声影响以较低增益读出的概率曲线图Fig.2 Probability curve of low gain readout of pixels affected by noise

多挡增益光谱成像系统的动态范围和信噪比有如式(11)关系

$\{\begin{array}{l} R_{D} (λ, i) = \frac{N_{FW} (λ, i)}{N_{noise} (λ, i)} \\ R_{SN} (λ, i) = \frac{N_{signal} (λ, i - 1)}{\sqrt[]{N_{signal} (λ, i - 1) + N_{noise}^{2} (λ, i)}} \geq R'_{SN} \end{array}$ (11)

式(11)中, R_D(λ, i)为第i挡增益下的动态范围, R_SN(λ, i)和R'_SN分别为增益分界处的信噪比和该入瞳辐射水平下的信噪比指标。通常做法为在保证信噪比要求的前提下, 尽量提高动态范围。以上仿真的各个谱段的信噪比变化如图3所示。增益挡位分界处信噪比出现一定程度的下降, 这也是成像过程中的最极端情况。因此, 若该情形下的信噪比高于指标, 即可满足所有信噪比要求。

	Figure Option View Download New Window
	图3 各谱段的信噪比曲线图Fig.3 SNR curve of each spectrum segment

3 成像模拟实验及分析

3.1 成像模拟

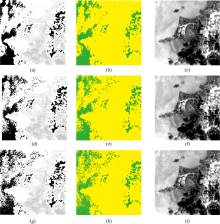
宽波段成像光谱仪(WIS)是天宫二号空间站上搭载的一台推扫式成像光谱仪^[10]。由于成像方式以及光谱通道等参数相近, 利用其L2级数据作为四挡增益成像模拟实验的入瞳辐亮度。如图4(a)—(i)所示, 第一列图像为WIS输入数据, 第二列为四挡增益光谱成像系统输出的DN值图像, 第三列为对应的增益挡位图。其中红、黄、绿、蓝分别表示高增益(满阱电荷为24 Ke^-)、中等增益(120 Ke^-)、低增益(600 Ke^-)、超低增益(2.5 Me^-)。若探测器最大电压V_max为1 V, 基底噪声电压V_noise为200 μV, 那么增益由高到低对应的噪声电子数分别为4.8 e^-, 24 e^-, 120 e^-和500 e^-。那么, 单级增益动态范围74 dB, 四挡增益的总动态范围为114 dB。通过大气传输模型MODTRAN仿真发现, 雪、积云等高亮目标的信号电子数约为7.62×10⁴~2.55×10⁶ e^-, 大洋水体等弱信号目标的信号电子数约为1.72×10⁴~1.70×10⁵ e^-。因此, 四挡增益光谱成像系统的动态范围完全满足综合性遥感监测的需求。

第一、二行图像选取的是太湖沿岸的同一区域, 中心波长分别为0.865和0.443 μm。在0.865 μm近红外波段, 水体主要处于高增益, 陆地为中等增益。而在0.443 μm蓝波段, 水体由于区域叶绿素浓度的不同处于中等和低两个增益挡位。不同于常规图像, 多挡增益图像中的白和黑不代表绝对的反射率大小。如图4(d)所示, 高叶绿素浓度的水体具有高反射率, 图中表现更亮。而在图4(e)中, 由于这部分区域超出中等增益挡位的满阱电荷, 以低增益读出的DN值反而小于低叶绿素浓度区域的水体, 图中呈现黑色。另外, 计算出0.443 μm谱段的系统响应参数低于0.865 μm, 但0.443 μm谱段地物反射率高于0.865 μm。相对于0.865 μm谱段, 0.443 μm成像需要更低的增益, 所以图4(f)为黄绿色, 图4(c)为黄红色。第三行图像选取的是上海滴水湖区域, 中心波长为0.682 5 μm, 整体处于低增益挡位。图中高亮部分为云层和建筑, 但其中只有少数高亮云层处于超低增益(蓝色)。

	Figure Option View Download New Window
	图4 逐像元多挡增益光谱成像模拟图Fig.4 Simulation image of pixel by pixel muli-gain spectral imaging

3.2 添加噪声

如图5所示, 根据噪声模型对中心波长为0.443 μm的光谱图像依次添加1~3σ 的随机噪声。 σ 包括光子噪声、读出噪声两个分量。 3σ 设置为对比需要, 实际成像结果应接近于1σ 。图5中第一列为添加噪声后的四挡增益DN值图像, 第二列为挡位图, 第三列为恢复出来的辐亮度图像。在通常系统设计指标中, 当辐亮度为7.02 mW· cm^-2· μm^-1· sr^-1(水体典型辐亮度), 光谱带宽为20 nm时, 信噪比要求大于500。经计算, 1~3σ 随机噪声下的信噪比分别为1 079.58, 539.79和359.86, 可以满足信噪比要求。

	Figure Option View Download New Window
	图5 添加1~3σ 随机噪声的成像模拟图Fig.5 Imaging simulation with 1~3σ random noise

噪声导致的增益挡位变化主要发生在水体区域, 其余区域的增益变化较小, 可见该图像中水体入瞳辐亮度较接近于中等增益(黄)和低增益(绿)的临界点。中等增益变成低增益的结果就是, 信号强度处于低增益挡位的底部, 同时具有更大的读出噪声, 导致信噪比下降。如图5(c), (f)和(i), 随着随机噪声的标准差增大, 恢复出的图像质量越差, 其中图5(i)水体区域的信噪比已经低于指标要求。

在图6中, 三幅图像均为3σ 随机噪声下放大的湖泊水体纹理特征。不同的是, 图6(a)是中心波长为0.94, 0.665和0.443 μm的三个谱段合并得到的, 图6(b)是中心波长为0.49, 0.443和0.413 μm的三个谱段合并得到的, 图6(c)是中心波长为0.443 μm的单个谱段。在同样噪声水平下, 图6(a)的纹理特征最为明显平滑, 而图6(c)几乎没有纹理特征。这是因为, 一方面多通道增加了光谱信息, 另一方面通道合并压缩了噪声。

	Figure Option View Download New Window
	图6 添加3σ 随机噪声后的水体纹理特征Fig.6 Lake texture features after adding 3σ random noise

4 结论

综合性遥感监测对于系统灵敏度和动态范围都具有较高的要求, 提出的逐像元多挡增益光谱成像方法可以很好地解决这一矛盾。在该方法的基础上建立了推扫式多挡增益光谱成像系统模型, 基于泊松-高斯噪声模型进行了跨挡读出的概率分析以及信噪比仿真。利用WIS数据作为入瞳辐射完成四挡增益的光谱成像模拟, 验证了该方法的可行性。四挡增益光谱成像系统总动态范围可达114 dB, 入瞳辐亮度为7.02 mW· cm^-2· μm^-1· sr^-1时的信噪比为1 079, 远高于一般指标。不足的是, 本文仅是基于理论模型进行仿真分析, 实际成像效果还要取决于系统搭建和辐射定标。这二者带来的误差对多挡增益光谱成像系统的影响还需进一步研究。

参考文献

文献列表

[1]	WANG Hong-bo(王宏博). Doctoral Dissertation(博士论文). University of Chinese Academy of Sciences(中国科学院大学), 2016. [本文引用:1]
[2]	WANG Jian-yu, WANG Yue-ming, LI Chun-lai(王建宇, 王跃明, 李春来). Journal of Remote Sensing(遥感学报), 2010, 14(4): 607. [本文引用:1]
[3]	YU Da, LIU Jin-guo, HE Xin, et al(余达, 刘金国, 何昕, 等). Acta Optica Sinica(光学学报), 2018, 38(11): 1104002. [本文引用:1]
[4]	ZHANG Yuan-tao(张元涛). Doctoral Dissertation(博士论文). University of Chinese Academy of Sciences(中国科学院大学), 2018, 13. [本文引用:1]
[5]	Qi Guanqiu, Chang Liang, Luo Yaqin, et al. Sensors, 2020, 20(6): 1597. [本文引用:1]
[6]	ZHOU Wang(周望). Acta Optica Sinica(光学学报), 2009, 29(3): 638. [本文引用:1]
[7]	SUN Wu, HAN Cheng-shan, JIN Xue-fei, et al(孙武, 韩诚山, 晋学飞, 等). Optics and Precision Engineering(光学精密工程), 2018, 26(4): 944. [本文引用:1]
[8]	Campana S B. Passive Electro-Optical Systems, The Infrared and Electro-Optical Systems Hand book, Volume 5, Environment Research Institue of Michigan & SPIE, 1993. [本文引用:1]
[9]	ZHOU Hong-chao, ZHU Ju-bo, WANG Zheng-ming(周宏潮, 朱炬波, 王正明). Chinese Space Science and Technology(中国空间科学技术), 2005, 4(2), 1. [本文引用:1]
[10]	He Xianqiang, Bai Yan, Wei Jun, et al. Optics Express, 2017, 25(20): 23955. [本文引用:1]

0.0

... 引言自20世纪80年代美国喷气推进实验室(JPL)研制出第一台机载成像光谱仪, 光谱成像技术开始在遥感领域得到大量应用^[1] ...

2010

0.0

... 例如王建宇等根据地物目标的辐射特性和系统灵敏度方程, 分析了高光谱成像系统中的各种噪声来源, 建立了空域、时域等多种噪声模型, 谱段范围包括可见光到热红外, 具有一定的普适性^[2] ...

2018

0.0

... 余达等将超高速电子倍增技术和成像光谱技术相结合, 构建了基于电子倍增的成像链模型, 并利用LOWTRAN7软件进行模拟仿真, 计算出该成像系统不同条件下的SNR, 从而选择适当的电子倍增增益^[3] ...

2018

0.0

... 例如美国S-NPP卫星上搭载的可见光红外成像辐射仪(VIIRS)设置有DNB通道, 为满足成像需求, 利用三挡增益同时获取目标信号, 对应的辐射增益为119 000:477:1^[4] ...

2020

0.0

... 由于成像系统与地面之间存在高速运动, 多次曝光^[5]、光强调制^[6]等常见的动态范围拓展方法无法适用^[7] ...

2009

0.0

... 由于成像系统与地面之间存在高速运动, 多次曝光^[5]、光强调制^[6]等常见的动态范围拓展方法无法适用^[7] ...

2018

0.0

... 由于成像系统与地面之间存在高速运动, 多次曝光^[5]、光强调制^[6]等常见的动态范围拓展方法无法适用^[7] ...

1993

0.0

... 如表1所示, 根据是否与曝光量相关, 可以将成像链路中的时域噪声分为两类^[8] ...

2005

0.0

... _i, 那么混合泊松-高斯分布的概率密度函数为^[9] ...

2017

0.0

... 1 成像模拟宽波段成像光谱仪(WIS)是天宫二号空间站上搭载的一台推扫式成像光谱仪^[10] ...