渭干河-库车河三角洲绿洲位于塔里木盆地北缘, 为典型的干旱区扇形平原绿洲, 辖区包括新疆维吾尔自治区阿克苏地区的库车市、 沙雅县和新和县, 北纬39° 30'-42° 40', 东经81° 27'-84° 07'。 土壤类型以潮土、 棕漠土、 灌淤土, 草甸土, 沼泽土和盐土等为主^[11]。 2019年7月中下旬以遥感影像及地形图为参考底图在研究区进行合理布点(图1)。 利用GPS系统对样点进行精准定位和现场调查。 每个采样点采集020 cm土层的土壤500 g左右, 共采集98个土壤样品。 将土壤样品带回实验室后经自然风干, 挑出杂物, 研磨并过筛后送至中国科学院新疆生态与地理研究所测试分析中心, 由工作人员通过重铬酸钾容量-外加热法对土壤有机质含量进行测定。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 采样点分布图Fig.1 Distribution of sampling points

采用ASDFieldSpec3光谱仪对土壤样品进行光谱采集, 其有效光谱范围为350~2 500 nm。 首先进行光谱仪的白板校正, 并尽量排除干扰土壤光谱的物体。 测量时, 按照标签顺序将土壤样品均匀摊开并完全覆盖在50 cm× 50 cm的牛皮纸上, 探头位于采样点的垂直上方, 距离为15 cm。 每个样品重复测量10条光谱曲线, 取其平均值作为该样品的光谱反射率。 为了避免所测光谱受背景干扰以及仪器等因素的影响而产生较大噪声, 剔除光谱曲线的两端数据, 同时考虑到水分对光谱反射率的影响, 又剔除了1 3411 400和1 8111 950 nm的水分吸收波段, 最终每份土样选取4002 450 nm范围内的1 901个光谱数据用于后续处理和分析。 进一步对原始光谱反射率(R)进行Savitzky-Golay (S-G) 5点平滑处理, 再采用倒数对数lg(1/R)、 一阶微分R'和倒数对数一阶微分[lg(1/R)]'以及连续小波变换(CWT)处理, 可有效减少外界因素对原始光谱反射率的干扰, 旨在快速寻找对土壤有机质含量敏感的有效波段。

连续小波变换(CWT)作为一种线性变换方法, 常应用于各类噪声信号的处理上, 具有一定程度的高分辨性和适应性, 其变换公式如式(1)和式(2)

Wf(a, b)≤fΨ(a, b)≥∫-∞+∞f(λ)Ψa, b(λ)dλ(1)

Ψa, b=1aΨλ-ba(2)

式中: λ 为高光谱波段数; a为尺度因子; b为平移因子; f(λ )为土壤光谱反射率; Ψ _{a, b}为小波基函数; W_f(a, b)为小波系数, 包含二维, 分别为波长(4002 450 nm)与分解尺度(1, 2, …, 10)。

通过The Unscrambler X软件使用偏最小二乘和支持向量机回归方法构建土壤有机质含量的估测模型, 其中偏最小二乘模型的最佳潜在变量依入选波段和小波系数的数量而定; 支持向量机回归函数可通过多次构建模型和模型调试后最终确定, 其中Cost惩罚参数为1, Gamma参数为0.01。 采用决定系数(R²)、 均方根(RMSE)和相对分析误差(RPD)检验模型的拟合效果和估测精度。 R²越大, RMSE越小, 则模型的精度越高, RPD越大则说明模型的预测能力越好^[12]。

依据全国第二次土壤有机质分级标准, 对研究区98个土壤样品按有机质含量的高低分为3个等级(< 6 g· kg^-1为极缺乏、 610 g· kg^-1为很缺乏、 1020 g· kg^-1为缺乏)。 通过分析有机质含量的基本特征(表1), 可以看出研究区总体样品土壤有机质含量在1.15017.582 g· kg^-1范围内变化, 即研究区土壤有机质含量在极缺乏和缺乏类别之间, 土壤有机质平均含量为8.574 g· kg^-1, 属于很缺乏水平。 分析认为研究区气候干旱、 降水稀少等因素导致土壤中微生物活性较低, 从而使有机质在土壤中的积累较慢, 土壤养分匮乏。 为了对研究区耕层土壤有机质含量的离散程度进行深入分析, 经计算土壤有机质的变异系数为41.86%, 属于中等程度的空间变异, 说明研究区土壤有机质含量的空间变异程度较高, 构建模型可具有代表性。

表1

Table 1

表1(Table 1)

表1 土壤样品的基本统计特征 Table 1 Basic statistical characteristics of soil samples 样品类型 样品数 /个 有机质含量/(g· kg-1) 变异系 数/% 最大值 最小值 平均值 标准差 总体样品 98 17.582 1.150 8.574 3.589 41.86

表1 土壤样品的基本统计特征 Table 1 Basic statistical characteristics of soil samples

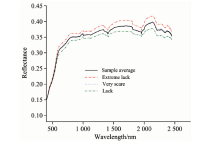
由于影响土壤光谱数据的因素较多, 在野外采集光谱数据后剔除较明显的受干扰波段, 并求出每个等级的光谱反射率平均值, 按照每个等级的平均光谱反射率做出不同等级的土壤光谱反射率曲线(图2)。 不同等级有机质含量的光谱曲线具有以下特征: (1)三个不同肥力级别的土壤光谱反射率曲线大致走向类似, 在4001 000 nm区间, 随着波长的增加, 反射率呈现上升趋势; 在1 000 nm以后, 除了水分吸收谷外, 曲线整体上较为平稳。 (2)在1 400, 1 900和2 200 nm附近存在水分吸收谷。 (3)土壤有机质含量与土壤的光谱反射率R呈负相关, 有机质含量越高, 土壤反射率越低。 本研究样品的平均值为8.57 g· kg^-1属于很缺乏级别, 故土壤样品平均值的光谱反射率与很缺乏曲线基本吻合, 说明土壤的光谱反射率与有机质含量具有明显的相关性, 土壤光谱反射率可准确反映有机质含量信息。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同等级有机质含量的光谱曲线Fig.2 Spectral curves of organic matter content in different grades

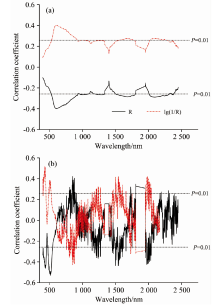
分别对原始光谱反射率R以及经lg(1/R)、 R'和[lg(1/R)]'转换的光谱反射率与土壤有机质含量进行相关性分析(图3)。 从图中可看出, R和lg(1/R)在可见光和近红外波段范围内有较多光谱波段可通过p< 0.01显著性检验, 其中大部分显著波段分布在可见光范围内。 通过对R和lg(1/R)与土壤有机质含量进行相关分析发现, 这两种光谱反射率与有机质含量之间的相关性并不高。 究其原因可能是土壤光谱数据在收集过程中无法避免会受到周围环境中的植被、 云层、 风力以及光照强度等因素的影响, 使得光谱信息被不同程度的干扰。 通过对原始光谱进行R', [lg(1/R)]'变换处理后, 其光谱反射率与土壤有机质含量之间的相关性有所提高, 通过p< 0.01显著性检验的波段零散分布在4302 100 nm范围内(表2)。 通过一阶微分变换可有效进行混合光谱的分解, 降低背景噪声的干扰或消除基线漂移, 有助于扩大样品之间的微小光谱特征差异, 提升光谱的识别能力以及有效波段的获取。 以4种光谱的特征波段反射率作为自变量, 土壤有机质含量作为因变量, 构建传统数学变换下的土壤有机质含量的偏最小二乘回归PLSR和支持向量机回归SVMR估测模型。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 土壤有机质含量与光谱反射率及其变换的相关性分析Fig.3 Correlation analysis of soil organic matter content with reflectance spectra and spectral transformations

表2

Table 2

表2(Table 2)

表2 不同变换下的特征波段 Table 2 The characteristic bands selected by different transformations 光谱变换 特征波 段数量 对应波段范围/nm 显著性水平 (p值) R 1 135 529933, 2 3512 382 < 0.01 lg(1/R) 1 137 526934, 2 3492 378 < 0.01 R' 318 431538, 800889, 1 4511 660, 1 9742 035 < 0.01 [lg(1/R)]' 293 431538, 795881, 1 7312 042 < 0.01

表2 不同变换下的特征波段 Table 2 The characteristic bands selected by different transformations

为了进一步探索土壤光谱与有机质含量之间的相关性, 对原始光谱反射率R进行连续小波变换, 光谱数据可分解成不同尺度, 有效去除了土壤高光谱数据中的白噪音。 由于小波基函数的选择对于原始光谱进行CWT较为重要, 相关学者选择不同小波母函数作为基函数对原始光谱反射率进行CWT处理, 从而得到了较好的预测结果^{[13, 14]}。 研究采用Bior1.3, db4, Gaus4和mexh等基函数, 对原始光谱反射率R进行多次小波变换实验, 其中以Bior1.3为基函数的小波变换结果较为理想, 故选择小波变换基函数为Bior1.3函数。 通过MATLAB编程, 对原始光谱反射率R进行CWT处理, 为了减少数据冗余, 尺度分别选择2¹, 2², 2³, …, 2¹⁰, 并对生成的小波变换后的光谱数据(即小波系数)与土壤有机质含量进行相关性分析(见图4)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 土壤有机质含量与小波系数的相关性Fig.4 The correlation between soil organic matter content and wavelet coefficients

通过对CWT分解后的10种尺度的小波系数与土壤有机质含量进行相关分析, 发现各尺度的小波系数与土壤有机质含量之间的相关性较传统数学变换处理有所提高, 相关性较高的区域主要位于410525, 790890, 1 2441 274和2 0082 038 nm处。 从不同尺度来看, CWT分解后的光谱反射率与有机质含量之间的相关性较高的区域出现在14尺度的可见光波段和57尺度的近红外波段, 第810尺度下的CWT处理对提升光谱与有机质含量之间的关联性无明显作用。 经各分解尺度变换后, 通过p< 0.01显著性水平检验的小波系数总数为2 719个。 同时, 从图4中可以看出原来与土壤有机质含量只存在负相关关系的原始光谱反射率R, 通过CWT处理后各尺度都存在一定的正负相关性。 分析说明, CWT处理能有效放大光谱中的微妙信号, 更有利于获取土壤中有机质含量信息。

分别以特征波段的原始光谱反射率R和三种传统数学变换下的光谱反射率以及经过CWT分解后选取的敏感小波系数作为自变量, 土壤有机质含量作为因变量, 通过偏最小二乘回归(PLSR)和支持向量机回归(SVMR)方法构建土壤有机质含量估测模型。 为了找出原始光谱反射率R经CWT变换后建模的最佳尺度, 把各个尺度上的敏感小波系数单独作为自变量建立估测模型。 通过建模软件选取约30%的样品作为交叉验证样品集, 用于检验模型的估测精度。 因CWT处理后, 以2⁸, 2⁹, 2¹⁰尺度下的小波系数作为自变量建立的反演模型精度低且不稳定, 决定系数小于0.4, 故在最终结果中没有展示。 分别以不同变换下的特征波段与不同尺度下的敏感小波系数作为自变量建立的反演模型, 其建模和验证结果如表3所示。

表3

Table 3

表3(Table 3)

表3 土壤有机质含量反演模型的建模集与验证集结果 Table 3 Inversion results of modeling set and validation set for soil organic matter content 模型 建模集 验证集 RPD R2 RMSE R2 RMSE R-PLSR 0.59 2.29 0.46 2.96 1.55 R-SVMR 0.61 2.90 0.32 2.92 1.23 lg(1/R)-PSLR 0.58 2.31 0.46 2.64 1.54 lg(1/R)-SVMR 0.63 2.23 0.31 2.99 1.60 R'-PSLR 0.61 2.24 0.46 2.64 1.59 R'-SVMR 0.69 2.05 0.48 2.59 1.74 [lg(1/R)]'-PLSR 0.61 2.23 0.46 2.62 1.60 [lg(1/R)]'-SVMR 0.72 1.93 0.53 2.44 1.85 R-CWT-21-PLSR 0.68 2.02 0.46 2.63 1.77 R-CWT-21-SVMR 0.79 1.68 0.52 2.48 1.92 R-CWT-22-PLSR 0.61 2.23 0.48 2.64 1.72 R-CWT-22-SVMR 0.82 1.56 0.56 2.38 1.98 R-CWT-23-PLSR 0.63 2.18 0.46 2.62 1.73 R-CWT-23-SVMR 0.84 1.49 0.53 2.38 2.11 R-CWT-24-PLSR 0.65 2.11 0.52 2.57 1.86 R-CWT-24-SVMR 0.87 1.37 0.50 2.44 1.91 R-CWT-25-PLSR 0.65 2.11 0.55 2.40 1.89 R-CWT-25-SVMR 0.85 1.44 0.47 2.53 1.99 R-CWT-26-PLSR 0.65 2.12 0.56 2.39 1.88 R-CWT-26-SVMR 0.85 1.45 0.50 2.53 1.86 R-CWT-27-PLSR 0.60 2.25 0.51 2.50 1.58 R-CWT-27-SWMR 0.80 1.64 0.41 2.74 1.97

表3 土壤有机质含量反演模型的建模集与验证集结果 Table 3 Inversion results of modeling set and validation set for soil organic matter content

通过分析表3可知, 以原始光谱反射率R与倒数对数lg(1/R)为自变量的PLSR和SVMR模型的决定系数R²较小, 而通过一阶微分变换后模型的精度显著高于前者, 其中[lg(1/R)]'-SVMR模型的建模集和验证集决定系数R²分别为0.72和0.53, 均方根误差RMSE分别为1.93和2.44, 相对分析误差RPD为1.85, 说明以倒数对数一阶微分变换处理后构建的模型拥有较高的估测精度, 但是模型的预测能力一般。 以CWT处理下的不同尺度(2¹, 2², 2³, …, 2⁷)敏感小波系数为自变量的估测模型, 其建模集和验证集的估测精度较传统数学变换有所提高, R²和RPD增大, RMSE减小, 预测能力提升明显。 且经CWT处理后的SVMR模型在第2, 3, 4, 5, 6和7分解尺度下的建模集决定系数均可达0.8以上, 相对分析误差RPD大于1.8, 说明这些模型均具有较高的估测能力和稳定性。 其中, 第3尺度R-CWT-2³-SVMR模型的估测精度最高, 稳定性最好。 综合分析各模型估测结果认为, 经CWT处理后的模型精度明显优于传统数学变换后的模型, SVMR模型的精度高于PLSR模型。

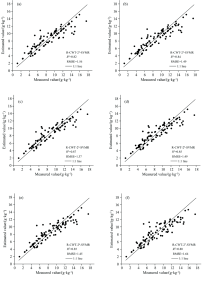
为了更好地展示模型的估测结果, 选择第2, 3, 4, 5, 6和7分解尺度下估测效果较好的SVMR模型, 分别以样本实测值与估测值作为横纵坐标做出散点图(见图5)。 从图中可清晰地看到模型的估测值和实测值基本分布在1:1拟合线附近, 散点分布较为集中, 模型估测精度较高。 综合分析认为, 利用CWT分解后的高光谱数据结合SVMR方法建立的模型估测精度较高, 可有效反演土壤有机质含量信息。 在以第3尺度敏感小波系数为自变量建立的R-CWT-2³-SVMR模型中, 决定系数R²相较于原始光谱建模结果提升了0.23, 均方根误差RMSE降低了1.41, 模型的相对分析误差RPD达到了最大(值为2.11), 预测能力很好。 分析说明, 经CWT第3尺度分解处理后的SVMR模型可作为研究区土壤有机质含量的有效估测模型。 通过多种变换处理, 在不同程度上可有效提高光谱反射率与土壤有机质含量的相关性以及反演模型的估测精度; 相较于传统变换方法, 多种分解尺度下的连续小波变换处理能明显消除不确定性因素对光谱信息的干扰, 从而快速提升反演模型的预测能力和适用性^{[15, 16]}。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 CWT下的土壤有机质含量实测值与估测值比较Fig.5 Comparison of measured and estimated values of soil organic matter content using CWT