In this study, 140 soil samples were collected in Shanxi Province (Taigu, Guandishan, Youyu, Loufan, Ningwu) at a depth of 5~15 cm above the ground. All soil samples were air-dried and divided into two groups evenly. One group was used for SOM content detection. The other was used to prepare soil samples with a moisture content of 0%, 5%, 10%, 15%, and 17%. The SOM content is tested by the potassium dichromate method(National standard method of China, GB9834— 88). The statistic results show thatthe maximum content of organic matteris 63.98, the minimum is 4.02, the average is 19.475, and the standard deviation is 14.043.

The Field Spec3 spectrometer developed by the American ASD company was used to collect the spectral data of the soil samples. The main working parameters of the instrument are: spectral scanning range is 350~2 500 nm; data interval is 1 nm. After the spectrometer was preheating and stabilizing, soil sample was placed in a petri dish and scraped flat for spectrum collection. The whole spectral scanning process was carried out at room temperature. MATLAB_R2014b software was used for data analysis.

Extraction of characteristic wavelengths can simplify the model, and more importantly, it can eliminate irrelevant or nonlinear variables. However, the wavelength obtained by different extraction methods always fluctuates within a range, and the space with a small fluctuation range is always the effective characteristic band. Therefore, this paper proposes an algorithm that takes the integral absorbance value at characteristic wavelength as the independent variable and establishes the model. It eliminates the local optimization defect of the characteristic wavelength extraction algorithm to a certain extent. The specific steps are as follows:

(1) Obtain the sensitive wavelength by using spectral characteristic wavelength extraction algorithm;

(2) Take the extracted characteristic wavelength value as the center, and calculate the approximate area surrounded by the spectral curve by taking a left and right n nm. The area of the rectangle is obtained by taking the difference of adjacent wavelengths as one side of the approximate rectangle and the corresponding absorbance value as the other side;

(3) Sum of all areas and take it as an independent variable.

The integration algorithm can be expressed as follows:

∫Aλ=∑i=-mi=mAλ+i×r(1)

This formula, A_λ represents the absorbance value of the spectrum at the wavelength λ , i is the integration variable, mis the integration range, and ris the data interval of the spectrum curve measured by the spectrometer, here is 1 nm.

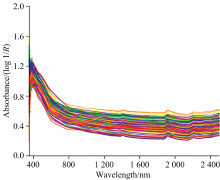
ASD company’ s software View Spec Pro 6.0 was used for spectral preprocessing, and the spectra were obtained after the mean, splicing correction and spectral reflectance logarithm operation.The spectral data of 140 dry soil samples are shown in Fig.1. It can be seen that all samples have typical soil spectral characteristics, the visible light range (350~780 nm) curve shows a clear downward trend, the near-infrared band (780~2 500 nm) spectral curve is relatively flat, and there are obvious absorption peaks near 1 400, 1 950 and 2 200 nm.

Fig.1

	Figure Option ViewDownloadNew Window
	Fig.1 Spectra of all the 140 soil samples

2.1.1 Characteristic Wavelength Extraction

Successive projections algorithm(SPA) is a common and effective method of extracting characteristic wavelengths. This method uses projection analysis of vectors to select effective wavelengths with minimum redundancy and minimum collinearity^[13]. Since the noise in the initial range of the instrument is generally high^[1], the absorbance value in the range of 400~2 500 nm is selected as the research object in this paper.

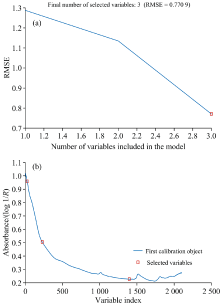
The root means square error (RMSE) distribution curve obtained by extracting characteristic wavelength with SPA and the extraction result of characteristic wavelength are shown in Fig.2. The red block in Fig.2 indicates the number and value of selected characteristic wavelength respectively. The extracted characteristic wavelengths are 627, 425, and 1 796 nm in order of importance, of which 627 nm is consistent with Wang’ s two-dimensional spectral extraction results^[11], 425 nm is mainly due to the influence of goethite and hematite in soil components^{[14, 15]}, and 1 796 nm is affected by the content of lignin in soil^[16].

Fig.2

	Figure Option ViewDownloadNew Window
	Fig.2 The RMSE and characteristic wavelengths distribution curves after SPA

2.1.2 SOM prediction model

According to the extracted characteristic wavelengths, the absorbance value of characteristic wavelength and the integral absorbance values at characteristic wavelength are used as independent variables for modeling. The SPXY (sample set partitioning based on joint x-y distance) algorithm divides 110 dry samples for modeling and 30 dry samples for prediction. Since only three characteristic wavelengths are extracted in this study, multiple linear regression (MLR) is selected as the modeling method. In addition, MLR has more advantages in the later instrument development for its simple calculation.

The equations fitted by the two methods are as follows, which model (Ⅰ ) is used the absorbance value of characteristic wavelength and model (Ⅱ ) is used the integral absorbance values at a characteristic wavelength. The statistical parameters are shown in Table 1.

Table 1

Table 1

Table 1 Comparison of statistical parameters in wavelength and integration modeling Modeling method independent variable RC RMSEC/ (g· kg-1) RP RMSEP/ (g· kg-1) SPA+MLR(model Ⅰ ) Absorbance value at characteristic wavelength 0.935 0 3.382 0.901 4 4.104 SPA+MLR(model Ⅱ ) Absorbance integral value at characteristic wavelength (integration range is 5 nm) 0.935 8 3.343 0.902 2 4.020 y=34.898+369.206A637-189.129A452-176.623A1796(Ⅰ)y=35.443+33.553∫A627-17.242∫A452-16.068×∫A1796(Ⅱ)

Table 1 Comparison of statistical parameters in wavelength and integration modeling

Where y represents the SOM content. A₆₂₇, A₄₅₂, A_{1 796} respectively represent the absorbance values of soil samples at the wavelengths of 627, 452 and 1 796 nm. ∫A627, ∫A452, ∫A1796are the integral absorbance values of soil samples at the wavelengths of 627, 452, and 1 796 nm respectively.

It can be seen from the statistical parameter table that R_P is increased and RMSEP is reduced when the absorbance integral value at characteristic wavelength is taken as the independent variable. Sousing the integral value as an independent variable can make the model more robust.

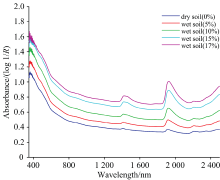
The average spectra of 140 wet soil samples with different moisture contents are shown in Fig.3. It can be seen from the figure that with the increase of soil moisture, the absorption peaks that appear near the water-sensitive bands of 1 415, 1 929, and 2 210 nm are quite obvious, which is consistent with the research results of Wang^[11].

Fig.3

	Figure Option ViewDownloadNew Window
	Fig.3 Average spectra of wet soil samples with different moisture content

2.2.1 Reconstruction of wet soil spectrum

As soil moisture has obvious absorption peaks around 1 415, 1 929, and 2 210 nm^[11], the absorbance values at these three wavelengths construct the soil moisture correction coefficient. The specific algorithm of the correction coefficient is as follows:

MCC=A2210A1929+A1415×∫A1929+∫A1415∫A2210(2)

Where MCC represents the moisture correction coefficient, A_{2 210}, A_{1 929} and A_{1 415} respectively represent the absorbance values of the wet soil samples at the wavelengths of 2 210, 1 929, and 1 415 nm, ∫A1929, ∫A1415and ∫A2210are the integral absorbance values of the wet soil samples at the wavelengths of 1 929, 1 415, and 2 210 nm respectively, and the corresponding integer values are obtained by formula (1).

Reconstruct the spectrum of wet soil using the following formula:

RWSλ=WSλ-MCC×∑(WSλ-DSλ)n(3)

Where RWS_λ is absorbance values at wavelength λ of samples with different moisture content after correction; WS_λ and DS_λ are the absorbance values of wet soil and dry soil under corresponding wavelength λ , andnis the number of samples.

The reconstructed spectral curves are shown in Fig.4(a)— (d) (taking the organic matter content of 32.57 g· kg^-1 as an example). It can be seen that the peak value of the reconstructed spectra in the water-sensitive band decreases significantly and is closer to the spectral curve of dry soil. In addition, when the moisture content is high (such as 15%, 17%), the correction effect of this method is better than Hu^[17]. The results show that this method can solve the influence of different moisture content on the change of soil spectral absorbance.

Fig.4

	Figure Option ViewDownloadNew Window
	Fig.4 Spectra of reconstructed soil sample in different moisture content (taking the organic matter content of 32.57 g· kg-1 as an example) (a): 5%; (b): 10%; (c): 15%; (d): 17%

2.2.2 Prediction model and evaluation of wet soil

In order to verify the prediction effect of the two models for wet soil samples, the measured and predicted values of organic matter in wet soil were fitted and analyzed (Fig.5). Among them, Fig.5(a) is model Ⅰ , Fig.5(b) is model Ⅱ . In Fig.5, wet soil samples are marked red, and the corrected wet soil samples are marked with blue. The closer the fitting result is to 1∶ 1 (line in the figure), the higher the accuracy of model prediction is, and the related statistical parameters are shown in Table 2.

Fig.5

	Figure Option ViewDownloadNew Window
	Fig.5 Wavelength modeling (a) and integral modeling (b) comparison of SOM measured and SOM predicted values

Table 2

Table 2

Table 2 Comparison of prediction model parameters of SOM in wet soil Modeling method independent variable predicted samples RP RMSEP/(g· kg-1) SPA+MLR(model Ⅰ ) Absorbance value at characteristic wavelength Original wet soil Reconstructed wet soil 0.781 7 0.864 8 5.325 3.697 SPA+MLR(model Ⅱ ) Absorbance Integral value at characteristic wavelength Original wet soil Reconstructed wet soil 0.788 3 0.871 1 5.260 3.609

Table 2 Comparison of prediction model parameters of SOM in wet soil

It can be seen from Fig.5 that the soil moisture correction algorithm can effectively eliminate the moisture affection on SOM prediction. The R_P increased by about 0.08 and RMSEP decreased by about 1.63 g· kg^-1 in both model Ⅰ and model Ⅱ . Compared with using the absorbance value at characteristic wavelength as the independent variable, the model established by using the integral value as the independent variable has better correlation (R_P) and lower error (RMSEP) for prediction results. It shows that model Ⅱ contains more effective information about the SOM than model Ⅰ .