引用本文
奚亮, 司福祺, 江宇, 周海金, 邱晓晗, 常振. 基于权重变分模型的地基IDOAS条带噪声去除[J]. 光谱学与光谱分析, 2022,42(2): 627-633.
XI Liang, SI Fu-qi, JIANG Yu, ZHOU Hai-jin, QIU Xiao-han, CHANG Zhen. Ground-Based IDOAS De-Striping by Weighted Unidirectional Variation[J]. Spectroscopy and Spectral Analysis, 2022,42(2): 627-633.
Doi:10.3964/j.issn.1000-0593(2022)02-0627-07  
Permissions
Copyright©2022, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于权重变分模型的地基IDOAS条带噪声去除
奚亮1,2, 司福祺1,*, 江宇1, 周海金1, 邱晓晗1, 常振1
1.中国科学院合肥物质科学研究院, 安徽光学精密机械研究所, 安徽 合肥 230031
2.中国科学技术大学, 安徽 合肥 230026
*通讯作者 e-mail: sifuqi@aiofm.ac.cn

作者简介: 奚 亮, 1991年生, 中国科学院安徽光学精密机械研究所博士研究生 e-mail: lxi@aiofm.ac.cn

收稿日期: 2021-01-11 修回日期: 2021-02-24 接受日期: 2021-02-24
基金: 国家重点研发计划项目(2018YFC0213201, 2019YFC0214702)资助
摘要

成像差分吸收光谱技术是成像光谱技术和差分吸收光谱技术的结合, 能够采集图谱合一的数据立方, 并通过光谱反演得到痕量气体浓度的二维分布信息。 地基IDOAS仪器通过安装平台的水平旋转实现摆扫成像, 可用于识别污染气体的排放源和监测气体的扩散情况。 然而和所有的成像光谱技术相类似, 地基IDOAS也容易出现条带噪声的问题, 会产生相应的伪结构, 影响后续的信息提取和数据分析。 目前星载和机载IDOAS中常见的条带噪声去除算法有均匀区域校正法、 传输模型模拟法、 傅里叶变换频域滤波法、 多项式拟合法等, 应用到地基仪器中均存在不适用的问题。 介绍了一种基于权重变分模型的条带噪声去除算法, 该算法首先通过分块自适应阈值分割得出表征遮挡区域的权重矩阵, 然后利用条带噪声的方向性和稀疏性建立各向异性的变分模型, 最后通过交替方向乘子算法迭代求解。 为检验去条带算法的可靠性, 使用稀疏、 稠密、 周期、 随机、 整行、 部分、 单行、 多行等多种模拟噪声进行了性能测试。 测试结果证明权重变分算法能够有效去除各种常见的条带噪声, 目视效果和四种全参考评价指标均有良好的表现。 地基IDOAS于2018年夏季在四川乐山进行了外场实验, 实验中仪器的水平扫描范围覆盖360°全方位角, 扫描间隔为1°, 垂直方向仪器同时采集0°~30°仰角内的光谱。 仪器的积分时间设置为500 ms, 每组全景扫描的工作时间约为15 min。 利用DOAS技术对采集到的太阳散射光谱进行反演, 最终得到的NO2和SO2气体的二维浓度分布图的像素大小为360×48。 从反演结果来看, 条带噪声对不同时间和不同气体的观测结果的影响大小均不同。 经权重变分算法处理后, 多组NO2和SO2浓度分布中的条带噪声情况得到极大的改善, 并且没有出现过度平滑的情况。 结果表明, 该算法适用于地基IDOAS数据的条带噪声去除。

关键词: 成像差分吸收光谱; 条带噪声; 变分法; 光学遥感
中图分类号:O433 文献标志码:A
Ground-Based IDOAS De-Striping by Weighted Unidirectional Variation
XI Liang1,2, SI Fu-qi1,*, JIANG Yu1, ZHOU Hai-jin1, QIU Xiao-han1, CHANG Zhen1
1. Anhui Institute of Optics and Fine Mechanics, Hefei Institutes of Physical Science, Chinese Academy of Sciences, Hefei 230031, China
2. University of Science and Technology of China, Hefei 230026, China
*Corresponding author
Abstract

Imaging differential optical absorption spectroscopy technology (IDOAS) combines imaging spectroscopy and differential optical absorption spectroscopy. The acquired data of IDOAS instruments are so-called hyperspectral cube with two spatial dimensions and a spectral one. After DOAS analysis of the original data, two-dimensional trace gas distributions can be resolved. For ground-based IDOAS instruments, the imaging capability is achieved through the stepwise rotation of the motor in the horizontal direction, which can be used to identify the emission sources of polluting gases and monitor the transmission of pollution. However, similar to other imaging spectroscopy instruments, ground-based IDOAS instruments are also prone to stripe noise, producing corresponding pseudo-structures and affecting subsequent information extraction and data analysis. Several de-striping algorithms have been applied for space-borne and airborne sensors, including homogeneous reference area correction method, transmission model simulation method, frequency domain filtering method, polynomial fitting method, which are not fully applicable to ground-based instruments. Here we present a de-striping algorithm based on a weighted unidirectional variation model. This algorithm first obtains a weight matrix that characterizes the blocked area through adaptive threshold segmentation, then utilizes the unidirectionality and sparsity of the strip noise to establish the optimization model, which is solved iteratively by using the alternating direction method multipliers technique. To test the performance of the de-striping algorithm, simulated experiments were performed using various cases including sparse, dense, periodic, random, whole-line, partial, single-line, multi-line stripe noise. Corresponding results prove that this algorithm can effectively remove typical stripe noise, with good performances in visual and four full-reference evaluations. Ground-based IDOAS observations were carried out in Leshan, Sichuan province, in the summer of 2018. In this experiment, the IDOAS instrument provided a full-azimuthal coverage (360°) and a 30° vertical coverage around the measurement site. The acquisition time of a full-panoramic image was about 15 min when the integration time was set to 500 ms. The final panoramic views of NO2 and SO2 columns consist of 48 vertical and 360 angles on the horizontal axis. According to the real data results, the stripe noise changed greatly for different gases at different times. After de-striping by this weighted variation algorithm, the stripe noise in the NO2 and SO2 columns reduced greatly without over-smoothing. Experimental results of the real data demonstrate that this algorithm is suitable for de-striping of ground-based IDOAS data.

Keyword: Imaging differential optical absorption spectroscopy; Stripe noise; Variation; Optical remote sensing
引言

成像差分吸收光谱技术(imaging differential optical absorption spectroscopy, IDOAS)是成像光谱技术和差分吸收光谱技术的结合, 作为一种测量大气痕量气体(SO2, NO2, O3等)的有效方法, 能够获取痕量气体二维浓度分布信息, 近年来在地基、 机载和星载平台均有较大的发展[1, 2, 3]。 受到传感器不均匀性和外界环境变化等因素的影响, IDOAS仪器容易出现条带噪声。 作为一种在成像光谱技术中常见的数据降质问题, 条带噪声会覆盖目标物的空间分布特征并产生相应的伪结构, 影响后续的反演分析和信息提取, 最终降低了数据的可用性。

为解决条带噪声问题, 国内外已有学者提出了有效的处理算法。 在星载方面, Boersma等利用洁净均匀区域的平均值作为真值, 计算不同探测像元和真值的差值来消除OMI NO2柱浓度中的条带噪声[4]; Cheng等为去除EMI NO2产品中的条带噪声, 使用了二维傅里叶变换加频率滤波的方法[5]; 杨太平等将SICATRAN模型的模拟值作为参考, 实现了EMI O4产品穿轨方向的条带校正[6]; Geffen等在TROPOMI NO2算法中, 将太平洋赤道地区的斜柱浓度与CTM/DA模型计算值的差异作为去条带的校正系数[7]。 在机载方面, Popp等假定APEX观测结果在穿轨方向上平滑变化, 对沿轨方向的均值进行多项式拟合后, 最后从NO2柱浓度中减去残差结构以去除条带[8]; Nowlan等在GeoTASO NO2柱浓度的去条带算法中, 利用洁净海湾区域的观测值与CMAQ模拟值的偏差作为校正量[9]。

以上算法均有良好的去条带效果, 然而在应用到地基IDOAS中却存在一些不适用的问题, 如均匀参考区域难以获得, 地面遮挡物造成的异常区域较多, 条带噪声变化较大等。 本文将图像处理中常用的变分模型应用到地基IDOAS仪器的条带去除中[10], 在考虑了条带噪声的分布特性和地基仪器的的遮挡问题后, 提出了基于权重变分模型的去条带算法。 经过模拟实验和外场实验的测试, 该算法能够有效去除地基IDOAS仪器中气体浓度分布的条带噪声问题。

1 基本原理
1.1 地基IDOAS原理

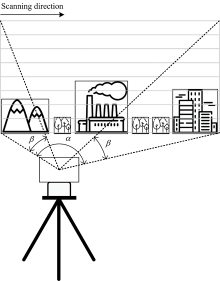
如图1所示, 地基IDOAS通过二维转台的水平旋转实现摆扫成像, 其中箭头表示扫描的方向, α 表示水平方向上扫描的角度, β 表示垂直方向上的视场角。 仪器采集天空中的太阳散射光, 并利用DOAS方法处理光谱得到痕量气体沿光路的积分浓度。 DOAS技术的原理是Lambert-Beer定律[11], 利用痕量气体的窄带吸收特性, 将其与Mie散射、 Rayleigh散射、 气溶胶作用等宽带信号相分离。 图2为一组外场实验的观测结果, 实验中IDOAS仪器水平扫描360° , 垂直方向覆盖30° 。 图2(a)为360 nm处探测器接收到的数字值(digital number, DN), 图2(b)为地面障碍物分布, 图2(c)和(d)为NO2和SO2的观测结果, 图2(e)和(g)为NO2观测结果的垂直和水平梯度图, 图2(f)和(h)为SO2观测结果的垂直和水平梯度图。

图1 地基IDOAS仪器示意图Fig.1 Scheme of ground-based IDOAS instrument

图2 地基IDOAS一组观测结果
(a): 360 nm处DN值; (b): 权重矩阵; (c): NO2浓度; (d): SO2浓度; (e): NO2浓度的垂直梯度; (f): SO2浓度的垂直梯度; (g): NO2浓度的水平梯度; (h): SO2浓度的水平梯度Fig.2 A set of patlerns observed by ground-based IDOAS observations
(a): DN values at 360 nm; (b): Weight matrix; (c): NO2 columns; (d): SO2 columns; (e): Vertical gradient of NO2 columns; (f): Vertical gradient of SO2 columns; (g): Horizontal gradient of NO2 columns; (h): Horizontal gradient of SO2 columns

1.2 条带噪声特性

从图2(c)和(d)可以看出, NO2和SO2观测结果有明显的条带噪声, 需要进行去条带处理。 与随机噪声相比, 条带噪声具有明显的空间分布特性, 如图2(e)— (h)所示, NO2和SO2观测结果在垂直方向的梯度远远大于水平方向的梯度。 同时条带噪声也具有稀疏性, 即条带噪声没有覆盖整幅图像, 且在很多区域接近于零。 此外, 对比图4中另外两组的观测结果, 可发现地基IDOAS中条带噪声不是固定的偏差值, 条带噪声的变化性较大。

图2(b)为观测点附近地表障碍物的分布, 障碍物的遮挡会造成光谱结构的改变, 使图2(c)和(d)中DOAS反演结果出现异常, 并使条带噪声的结构遭到破坏。 地基IDOAS测量中受到障碍物遮挡和气体空间分布的影响, 常见去条带算法中所需的均匀参考区域可能难以获得。 本文采用基于权重变分模型的去条带算法, 该算法利用条带噪声本身的分布特性, 不需要均匀的参考区域, 并使用权重矩阵解决了障碍物遮挡的问题。

1.3 权重变分去条带算法

假设条带噪声为加性噪声, 去条带算法的各向异性变分模型为

S^=argmin{‖∇hS‖1+λ1‖∇v(Y-S)‖1+λ2‖S‖0+λ3‖∇hS‖0}(1)

式(1)中: S为条带噪声; Y为观测到的实际图像; ∇h为水平梯度算子, ∇v为竖直梯度算子; ‖ · ‖ 1为l1范数, 能够在最小化的过程中接受较大的突变, 适合刻画条带边界。 ‖ · ‖ 0为l0范数, l0范数能控制S的估算过程, 避免无条带区域信息的丢失; 式(1)中右边第一项表示条带噪声在水平方向的连续性, 第二项表示图像在垂直方向上的连续性, 第三和第四项表示条带噪声及其水平梯度的稀疏性; λ 1, λ 2和λ 3为平衡方向性和稀疏性的参数。

式(1)利用图像的全局特性来估算条带噪声, 但在地基测量中由于异常区域的存在, 使得基于全局特性的算法不适用。 该异常区域由地表障碍物遮挡造成, 而在遮挡区域探测器的DN值通常要小于天空背景, 因此可通过阈值分割实现天空背景和地表障碍物的区分。 本文使用分块自适应阈值分割算法, 可得到表征遮挡区域的权重矩阵W。 如图2(b)所示, W在遮挡区域值为0, 在正常区域值为1。 在遮挡区域, 图像的方向特性遭到破坏, 因此可在式(1)中的前两项添加权重因子, 使其在遮挡区域的贡献为零。 结合以上分析, 权重变分模型可表示为

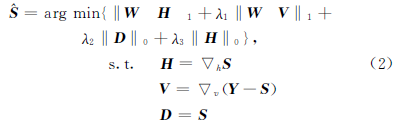
式(2)中: W为权重矩阵; °为元素乘法; H, V和D为引入的变量, 使式(2)转化为有约束的优化问题。 为求解式(2), 本文采用交替方向乘子算法(alternating direction method of multipliers, ADMM)[12], 其对应的增广拉格朗日展开为

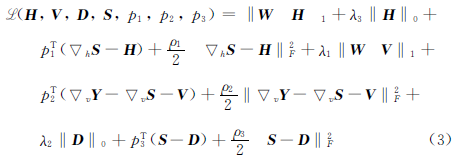
式(3)中: p1, p2和p3为拉格朗日乘子; ρ 1, ρ 2和ρ 3为惩罚参数。 原问题被分解为H, V, D和S四个相对简单的子问题, 并在迭代中交替求解

H(k+1)=cshrink∇hS(k)+p1(k)ρ1, Wρ1, 2λ3ρ1(4)

V(k+1)=softshrink∇vY-∇vS(k)+p2(k)ρ2, λ1Wρ2(5)

D(k+1)=hardshrinkS(k)+p3(k)ρ3, 2λ2ρ3(6)

式中cshrink, softshrink和hardshrink分别为复合阈值收缩、 软阈值收缩和硬阈值收缩算子[13], F和F-1分别表示二维快速傅里叶变换和逆变换; °为元素乘法; * 为复共轭算子。

在每轮迭代的最后, 需要按以下公式对拉格朗日乘子进行更新

p1(k+1)=p1k+ρ1(∇hS(k)-H(k))(8)

p2(k+1)=p2k+ρ2(∇vY-∇vS(k)-V(k))(9)

p3(k+1)=p3k+ρ3(S(k)-D(k))(10)

当迭代次数大于上限Nmax或S的变化量‖ S(k+1)-S(k)‖ /‖ S(k)‖ 小于阈值ε 时迭代停止。 从上述模型中估计出S后, 用实际图像Y减去S即可获得所需的去条带图像。

2 实验部分

为检验去条带算法的性能, 利用四种不同类型的模拟条带噪声进行了测试。 实验中理想图像为二维Savitzky-Golay滤波后模糊但无条带的实测数据, 图3展示了受不同模拟条带影响后的理想图像以及去条带结果, 其中图3(a)和图3(c)为位置周期、 强度随机的条带, 图3(a)中的条带较稀疏, 图3(c)中的条带较稠密; 图3(e)和图3(g)为位置周期、 强度随机的条带加上位置随机、 强度随机的条带, 图3(e)中的位置随机条带为部分条带, 即条带没有贯穿整行, 图3(g)中的位置随机条带为宽条跌, 即带宽度超过两行。 图3(a)— (h)中的底部灰色像元表示由遮挡所致的异常区域。

图3 不同模拟条带噪声和去条带结果
(a): 位置周期, 稀疏; (c): 位置周期, 稠密; (e): 位置周期+位置随机, 部分; (g): 位置周期+位置随机, 多行; (b), (d), (f), (h)为(a), (c), (e), (g)去条带结果Fig.3 Different simulated stripes and de-striping results
(a): Periodic position, sparse; (b): Periodic position, dense; (c): Periodic position+random position, partial; (d): Periodic position+random position, multi-line; (b), (d), (f), (h) are de-striping results of (a), (c), (e), (g)

在模拟实验中, λ 1, λ 2和λ 3分别设置为0.2, 0.001和0.2, ρ 1, ρ 2和ρ 3设置为100倍的λ 1, 最终去条带结果可见图3(b), (d), (f)和(h)。 从目视效果来看, 对四种不同类型的条带噪声, 权重变分算法都展现了良好的去条带性能。 采用四种常用的全参考评价指标对算法进行定量评价, 包括图像改善因子(improvement factor, IF)、 峰值信噪比(peak signal-to-noise ratio, PSNR)、 结构相似函数(structural similarity index, SSIM)和平均绝对误差(mean absolute error, MAE)[14]。 其中IF反映算法的降噪能力, 而PSNR, SSIM和MAE评价算法的保真能力。 一般来说, IF, PSNR的值越大, SSIM的值越接近于1, MAE的值越接近于0, 表明该算法的去条带效果越好。 表1列出了模拟实验中四种全参考指标计算结果, 不难发现权重变分算法都有良好的表现。 目视效果和评价指标均说明, 权重变分算法能够有效去除常见类型的条带噪声。

表1 模拟实验的评价结果 Table 1 Quantitative assessment of simulated data
3 结果与讨论

地基IDOAS于2018年夏季在四川乐山进行了外场实验, 图2(b)中从左到右的障碍物分别为信号塔、 山丘、 工厂烟囱以及其他建筑物。 工业园区位于仪器的西南方位, 分布着多个污染气体的排放源。 外场实验中仪器的扫描间隔为1° , 最终每组观测图像的像素大小为360× 48。 仪器的积分时间设置为500 ms, 每组全景扫描的总工作时间约为15 min。 在每组光谱采集完成后, 利用DOAS技术分别对NO2和SO2气体的斜柱浓度进行了反演, 具体的参数设置见表2。 图4展示了实验中两组观测的结果, 其中图4(a)和图4(c)为12:59开始采集的NO2和SO2浓度分布, 图4(e)和图4(g)为13:14开始采集的NO2和SO2浓度分布。 比较图4(a), (c), (e)和(g)可以发现, 条带噪声具有很大的变化性: 对于不同时间的观测结果, 条带噪声的空间分布和强度均不同; 对于不同反演气体, 条带噪声的空间分布和强度也不同。

表2 NO2和SO2 DOAS反演中的参数设置 Table 2 Main analysis parameters for NO2 and SO2 DOAS retrievals

图4 乐山实验中两组NO2和SO2的实际观测和去条带结果
(a): NO2浓度, 12:59开始采集; (c): SO2浓度, 12:59开始采集; (e): NO2浓度, 13:14开始采集; (g): SO2浓度, 13:14开始采集; (b), (d), (f), (h)为(a), (c), (e), (g)去条带结果Fig.4 Two groups of NO2 and SO2 observing and de-striping results in the Leshan experiment
(a): NO2columns, started at 12:59; (c): SO2 columns, started at 12:59; (e): NO2 columns, started at 13:14; (g): SO2 columns, started at 13:14; (b), (d), (f), (h) are de-striping results of (a), (c), (e), (g)

在权重变分模型中, λ 1, λ 2和λ 3用于平衡各个约束条件, 在实际应用中需根据图像的具体情况加以调整。 一般来说, 条带噪声的强度越大, λ 1应设置越大; 条带噪声越稀疏, 需使用更大的λ 2; 条带噪声越均匀, 适合用更大的λ 3。 在外场实验中为达到最佳的去条带效果, 经多次测试后λ 1, λ 2和λ 3分别设置为0.4, 0.001和0.2, ρ 1, ρ 2和ρ 3设置为100倍的λ 1。 去条带后的结果可见图4(b), (d), (f)和(h), 总体上去条带算法取得了令人满意的效果。 如图4(a)方框所示的多个浓度高值区域, 在去条带之后保留了各自的空间分布信息; 图4(c)方框所示的观测区域有大量的随机噪声, 在去条带之后没有变得模糊。 结果表明, 权重变分算法能够有效去除条带噪声, 能够保留污染气体分布信息, 且未出现过度平滑的情况。

图5展示了去条带前后的权重列均值曲线, 其中虚线为去条带前的权重列均值, 实线为去条带后的权重列均值。 权重列均值表示在计算图像X(大小为m× n)的列均值c时, 需考虑权重因子W, c的第i行分量为

ci=∑j=1nWi, jXi, j∑j=1nWi, j(11)

在低仰角区域会出现完全遮挡的情况, 此时定义分量ci为0。 从图5可以看出, 权重变分算法可以获得平滑的权重列均值曲线, 并且能保留原始曲线的变化趋势。

图5 去条带前后的NO2和SO2权重列均值对比
(a): NO2, 12:59开始采集; (b): SO2, 12:59开始采集; (c): NO2, 13:14开始采集; (d): SO2, 13:14开始采集Fig.5 Weighted mean cross-track profiles of NO2 and SO2 results before and after de-striping
(a): NO2, started at 12:59; (b): SO2, started at 12:59; (c): NO2, started at 13:14; (d): SO2, started at 13:14

由于实测数据没有理想图像作为参考, 为评估外场实验中去条带算法的有效性, 采用Borsdorff等提出的方法对结果进行定量评价, 参量γ 定义为[15]

γ=σ(∇vX)σ(∇hX)(12)

式(12)中, ∇vX和∇hX表示图像X的垂直梯度和水平梯度, σ 为计算标准差的算子。 ∇hX主要体现图像中像元之间的自然差异, 而∇vX会受到条带噪声的影响。 两者的标准差比值能反应去条带的效果, 当γ =1表示图像的像元间差异是各向同性的, 即条带噪声得到完全的去除。 表3列举了去条带前后, 考虑权重因子的γ 值。 不难发现, 去条带后四组图像的γ 值都普遍接近与1, 证明了权重变分去条带算法的有效性。

表3 去条带前后的γ 值 Table 3 γ values before and after de-striping
4 结论

针对地基IDOAS仪器中存在的条带噪声问题, 提出了基于权重变分模型的去条带算法。 该算法基于条带噪声的方向性和稀疏性, 不需要均匀的参考区域, 并充分考虑了地基成像中障碍物遮挡的问题。 在测试算法性能的模拟实验中, 对四组不同类型条带的降噪效果证明了该算法具有良好的有效性和保真性。 在2018年夏季的外场实验中, 地基IDOAS反演结果为痕量气体斜柱浓度的二维分布。 运用该算法后, 多组NO2和SO2浓度分布中的条带噪声得到了有效去除。 结果表明, 该算法适用于多种气体以及变化条带的情况, 提高了地基IDOAS观测数据的可用性。

参考文献
[1] Peters E, Ostendorf M, Bösch T, et al. Atmospheric Measurement Techniques, 2019, 12(8): 4171. [本文引用:1]
[2] LIU Jin, SI Fu-qi, ZHOU Hai-jin, et al(刘进, 司福祺, 周海金, 等). Acta Physica Sinica(物理学报), 2015, 64(3): 034217. [本文引用:1]
[3] Zhang C, Liu C, Chan K L, et al. Light: Science & Applications, 2020, 9(1): 66. [本文引用:1]
[4] Boersma K F, Eskes H J, Dirksen R J, et al. Atmospheric Measurement Techniques, 2011, 4(9): 1905. [本文引用:1]
[5] Cheng L, Tao J, Valks P, et al. Remote Sensing, 2019, 11(24): 3017. [本文引用:1]
[6] YANG Tai-ping, SI Fu-qi, Ping Wang, et al(杨太平, 司福祺, Ping Wang, 等). Acta Optica Sinica(光学学报), 2020, 40(9): 0901001. [本文引用:1]
[7] Geffen J V, Bosersma K F, Eskes H, et al. Atmospheric Measurement Techniques, 2020, 13(3): 1315. [本文引用:1]
[8] Popp C, Brunner D, Damm A, et al. Atmospheric Measurement Techniques, 2012, 5(9): 2211. [本文引用:1]
[9] Nowlan C R, Liu X, Leitch J W, et al. Atmospheric Measurement Techniques, 2016, 9(6): 2647. [本文引用:1]
[10] Chang Y, Yan L, Wu T, et al. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7018. [本文引用:1]
[11] Platt U, Perner D, Patz H. Journal of Geophysical Research, 1979, 84(10): 6329. [本文引用:1]
[12] Wahlberg B, Boyd S, Annergren M, et al. IFAC Proceedings Volumes, 2012, 45(16): 83. [本文引用:1]
[13] Song Q, Wang Y, Yan X, et al. Remote Sensing, 2018, 10(7): 998. [本文引用:1]
[14] Liu X, Shen H, Yuan Q, et al. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(2): 808. [本文引用:1]
[15] Borsdorff T, Brugh J A D, Schneider A, et al. Atmospheric Measurement Techniques, 2019, 12(10): 5443. [本文引用:1]