作者简介: 李明亮, 1995年生, 长春理工大学理学院硕士研究生 e-mail: 690617379@qq.com
为了提高铝合金定量分析的精度, 将激光诱导击穿光谱技术与多变量线性回归、 中值高斯核支持向量机回归及标准化偏最小二乘回归等方法相结合, 建立铝合金中 Cu元素定量分析模型。 对采集的LIBS光谱进行三阶极小值去背景和小波阈值降噪处理, 从而提高LIBS光谱的信背比。 将处理后数据筛选最佳训练集、 预测集并用多变量线性回归、 中值高斯核支持向量机回归法和标准化偏最小二乘拟合回归等建立定标模型。 选用 Cu Ⅰ 324.80 nm, Cu Ⅰ 327.43 nm两条特征谱线以及323~329 nm范围内的LIBS光谱数据进行定量分析, 对比分析三种LIBS定量分析模型的拟合系数( R2)、 定标均方根误差(RMSEC)、 预测均方根误差(RMSEP)和平均相对误差(ARE)等。 结果表明, 相对于多变量线性回归和中值高斯核支持向量机回归法两种LIBS定量分析模型, 对于铝合金中的Cu元素定量分析, 标准化PLSR模型的精度和准确度都有明显的提高, 并且LIBS定标曲线的 R2, RMSEC, RMSEP和ARE分别为0.997, 0.014 Wt%, 0.129 Wt%和3.053%。 研究结果表明在提高定标模型精确度与泛化性方面, 标准化PLSR方法更具有优势, 能够有效地减小参数波动和自吸收效应对铝合金定量分析的影响。
In order to improve the accuracy of quantitative analysis of aluminum alloy, a quantitative analysis model of Cu element in aluminum alloy was established by combining laser-induced breakdown spectroscopy with multivariate linear regression, median Gaussian kernel support vector machine regression and standardized partial least squares regression. Third order minimum background removal and wavelet threshold denoising were performed on the collected LIBS spectra to improve the SNR of LIBS spectra. The optimal training set and prediction set were selected from the processed data. The calibration model was established using multi variable linear regression method, medium Gaussian kernel support vector machine regression method and normalized partial least squares fitting regression method. Two characteristic lines of Cu Ⅰ 324.80 nm and Cu Ⅰ 327.43 nm and Libs spectral data in the range of 323~329 nm were used for quantitative analysis. The fitting coefficient ( R2), root mean square error (RMSEC), root mean square error of prediction (RMSEP) and average relative error (ARE) of the three Libs quantitative analysis models were compared and analyzed. The results show that compared with the multivariable linear regression method and medium Gaussian kernel support vector machine regression method, the precision and accuracy of the standardized PLSR model are significantly improved for the quantitative analysis of Cu element in aluminum alloy, and the R2, RMSEC, RMSEP and ARE of the Libs calibration curves are 0.997, 0.014 Wt%, 0.129 Wt% and 3.053%, respectively. The results show that the standardized PLSR method has more advantages in improving the accuracy and generalization of the calibration model, and can effectively reduce the influence of parameter fluctuation and self-absorption effect on the quantitative analysis of aluminum alloy.
铝合金是世界上用量和产量仅次于钢铁的有色金属, 其以强度高、 可塑性好等较多特点, 被广泛应用于航空航天、 建筑装饰、 电子通信等较多行业[1, 2, 3], 是国民经济发展的重要基础材料。 铝合金中的各种元素对其性能都有重要的影响, 如铜元素可以增强铝合金的硬度, 因此对铝合金中的组成元素进行定量分析是铝合金铸造过程中的重要环节。
传统的铝合金检测方法有电感耦合等离子体的原子发射光谱法、 质谱分析方法和原子吸收光谱法[4, 5, 6]等, 然而对于现场、 在线和离线分析, 这些方法都不是十分有效的。 激光诱导击穿光谱技术(laser induced breakdown spectroscopy, LIBS)具有实时在线、 快速检测、 无需样品预加工及多组分分析等优点, 被广泛用于土壤重金属污染及大气污染检测、 金属定量、 医学病症等分析领域[7, 8], LIBS技术可以实现对固、 液、 气三种形态样品的组成成分进行定性及定量分析[9, 10, 11]。 然而, 目前LIBS的实验重复性差问题, 极大地限制了其应用。 为了提高LIBS定量分析检测精度, Yao[12]等采用传统单变量方法及多变量偏最小二乘法(PLS)对污染猪肉中Cr, Pb元素进行定量分析, 发现LIBS技术结合PLS建模的方法有效降低了基质效应, 相比单变量方法预测精度有较大提升。 Owolabi[13]等提出极限学习机(ELM)与支持向量机回归(SVR)结合的方法对七块标准青铜样品进行定量分析, 通过引力搜索方法(GSA)进行参数优化, 发现ELM-SVR模型的浓度预测结果优于SVR-ELM, SVR及ELM。 为了进一步优化变量选取, Wang[14]等采用变量重要性度量结合随机森林(VIM-RF), 偏最小二乘法(PLS)及最小二乘支持向量机(LS-SVM)三种方法对酸性铁矿石进行定量分析, 发现VIM-RF方法相比PLS, LS-SVM模型具有更高的拟合系数值为0.910 3, 及更低的均方误差值为0.055 4 Wt%。 研究结果表明, 通过多个定标算法的结合可以提高LIBS检测精度, 对检测精度的进一步提高可以通过对原光谱数据的处理及定标函数内部的优化来实现。
本工作主要通过对原数据预处理及LIBS定量分析算法内部函数寻优来提高定标模型的精度和准确性。 对采集的LIBS光谱进行三阶极小值去背景和小波阈值降噪处理, 从而提高LIBS光谱的信背比。 将处理后数据筛选最佳训练集、 预测集并用多变量线性回归、 中值高斯核支持向量机回归法和标准化偏最小二乘拟合回归等, 建立铝合金中Cu元素的LIBS定量分析模型, 对比LIBS定量分析的拟合系数, 平均相对误差及均方误差值确定最优的LIBS定量分析模型。
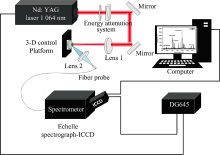
铝合金激光诱导击穿光谱实验装置如图1所示, 实验采用重复频率10 Hz、 脉宽10 ns、 输出波长1 064 nm的调Q Nd∶ YAG激光器(Continuum Power8000), 激光光束经二分之一波片和格兰棱镜组成的能量衰减系统后, 由焦距为120 mm的石英透镜聚焦到铝合金样品表面产生等离子体。 铝合金等离子体发射光谱由45° 放置的焦距75 mm的石英透镜进行光谱收集, 经光纤探头耦合进中阶梯光栅光谱仪(Andor, Mechelle 5000)光谱仪, 光谱分辨率为0.05 nm。 使用数字脉冲延时发生器DG645同步触发激光器和ICCD工作以及光谱采集时间延时。 实验参数设置如下, 脉冲能量为80 mJ, 光谱采集延时为800 ns, ICCD相机门宽为1 μs。 为防止铝合金靶材表面过度激光烧蚀, 靶材由三维平移台控制呈光栅式匀速扫描运动。 每组LIBS数据采集50发脉冲做平均, 相同实验条件下重复十一组。 所有的实验在标准大气压、 环境温度25 ℃、 相对湿度为40%参数下开展。 实验中所用样品为铝合金标样(购买于西南铝业集团有限责任公司, LD7.8系列), 物质含量符合国家标准, 表1为铝合金标样中Cu元素的质量浓度参数。
| 表1 LD7.8系列铝合金中铜元素的质量含量 Table 1 Copper concentration in aluminum alloy of LD 7.8 set |
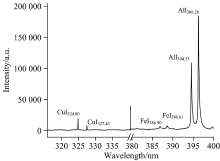
铝合金LIBS光谱如图2所示。 为减少仪器不稳定性及环境干扰等因素影响, 采用极小值背景扣除、 小波阈值法进行LIBS光谱基线去除和平滑降噪处理, 从而提高LIBS光谱的信背比, 并提高铝合金元素的LIBS探测精度。
2.2.1 多变量线性回归法
外标法属于传统的LIBS定标方法, 可以建立强度和浓度线性关系的LIBS定标曲线。 为了提升LIBS元素检测精度, 引入特征因子, 利用梯度下降法对两条Cu特征分析谱线 Cu Ⅰ 324.80 nm和 Cu Ⅰ 327.43 nm进行多变量线性回归, 见式(1)
2.2.2 支持向量机回归法
支持向量机法是建立超平面并对目标函数、 约束条件寻优从而实现线性划分。 当处理非线性回归问题时, 通过特征映射将非线性转为线性问题再进行分析, 引入核函数进行快速计算, 表示为
式(2)中, $ϕ[x^{(i)}]^{T}$与$ϕ[x^{(j)}]$为n维特征$x^{(i)}, x^{(j)}$映射到$\bar{n}$维的特征。 选用高斯核进行LIBS定量分析建模, 其核函数如式(3)所示
式(3)中, σ 为核宽, γ 为变换后的核尺度参数。 选用Medium Gaussian(高斯中值)核函数, 其对应核尺度参数表达式为γ mG=
2.2.3 标准化偏最小二乘回归法
偏最小二乘回归(PLSR)是一种多自变量X对多因变量Y的回归建模方法, 采用Z-score标准化PLSR模型进行浓度预测, 根据原LIBS光谱数据均值和标准差进行运算, 处理后的数据总体呈现标准正态分布。 将标准化后的数据代入到由传统偏最小二乘法(NIPALS)改进的简化偏最小二乘法(SIMPLS)中, 进行协方差矩阵信息提取及多次正交分解, 即可进行浓度预测, 如式(4)— 式(6)
其中E, F为Z-Score标准后的数据, tn和un分别为E和F的主成分对, wn和vn分别为E和F的主成分轴向量, 根据算得的W和R值代入新数据即可进行浓度预测。
基于LIBS技术在对元素含量进行定量分析时, 需要对LIBS定标模型的分析结果进行评价。 对于实验系统的精密程度或者实验的重复性, 用相对标准偏差(RSD)来表示; 元素的测量精度用均方根误差(root mean squared error, RMSE)表示, RMSEC为训练集均方根误差, RMSEP为预测集均方根误差。 平均相对误差(average relative error, ARE)用来表示元素测量浓度的准确度。
根据图2选用共振强度较高的Cu Ⅰ 324.80 nm和Cu Ⅰ 327.43 nm两条特征谱线进行定量分析, 根据均方根误差筛选得到编号1#, 3#, 4#, 5#, 7#, 8#, 9#, 11#的LIBS光谱数据作为训练集, 2#, 6#, 10#的LIBS光谱数据作为预测集, 采用多变量线性回归方法, 建立铝合金中Cu元素的LIBS定量分析模型, 得到由Cu Ⅰ 324.80 nm及Cu Ⅰ 327.43 nm两条谱线共同建立的Cu元素定标曲线如图3所示。
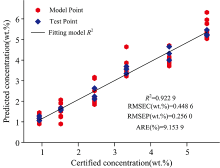 | 图3 多变量线性回归法建立的Cu元素定标曲线Fig.3 The calibration curve of Cu element used multivariable linear regression method |
图3定标曲线利用Cu Ⅰ 324.80 nm及Cu Ⅰ 327.43 nm两条谱线建立线性回归模型, 在保留LIBS光谱原信息基础上, 可提高LIBS定量分析的精确度, 获得的R2, RMSEC, RMSEP和ARE分别为0.922 9, 0.448 6 Wt%, 0.256 0 Wt%和9.153 9%。
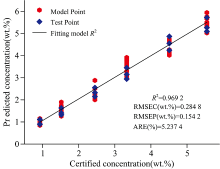
在多变量线性回归基础上, 选择Cu Ⅰ 324.80 nm及Cu Ⅰ 327.43 nm两条特征谱线, 采用中值高斯核SVR算法, 通过十倍交叉验证进行训练, 获得铝合金中Cu元素的LIBS定标曲线如图4所示。 由图4可知, SVR定标模型的离散程度变小, 定标曲线的相关拟合系数R2提高到0.969 2, RMSEC, RMSEP和ARE分别为0.284 8 Wt%, 0.154 2 Wt%和5.237 4%。
考虑增加提取光谱数据的变量数对LIBS定标分析精度的影响, 提取323~329 nm范围区间的 LIBS光谱谱段信息建立标准化PLSR定标分析模型, 获得铝合金中Cu元素的LIBS定标曲线如图5所示。 相比于多变量线性回归和中值高斯核SVR定标模型, 标准化PLSR的LIBS定标曲线的R2有了明显的提高, 提高到了0.996 61, 同时, RMSEC, RMSEP和ARE分别下降到了0.013 5 Wt%, 0.128 7 Wt%和3.052 8%。 多变量线性回归法、 中值高斯核SVR和标准化PLSR的三种LIBS定标模型参数对比如表2所示。
| 表2 多变量法、 中值高斯核SVR和标准化PLSR的三种LIBS定标模型参数对比 Table 2 Multivariable linear regression method, Medium Gaussian Kernel SVR method and the standardized PLSR method parameter comparison |
由表2可知, 铝合金中Cu元素的定量分析结果中, LIBS定标模型的线性拟合系数R2值满足
采用激光诱导击穿光谱技术对铝合金样品中的Cu元素进行定量分析。 在最佳实验条件(脉冲能量为80 mJ, 光谱采集延时为800 ns)下收集光谱信息, 针对与铜元素特征光谱信息并存的连续背景及噪声信息, 采用极小值背景扣除, 小波阈值法进行谱线基线去除、 平滑降噪。 将样品编号2#, 6#, 10#作为预测集, 其余组作为训练集进行定标, 将预处理后的数据分别代入到多变量线性回归、 中值高斯核函数SVR及标准化PLSR模型。 根据定标训练模型参数R2和RMSEC可以看出标准化PLSR得到的拟合系数R2最高, RMSEC最小, 说明该模型稳定性及拟合效果最佳。 根据定标预测模型参数RMSEP, ARE可以看出标准化PLSR具有最小的模型预测误差, 说明标准化PLSR模型具有相对较好的泛化性。 因此, 通过数据预处理及参数寻优后, 采用LIBS与标准化PLSR法相结合可以有效提高元素检测精度, 为工业铝合金多元素定量分析提供了一种参考方法。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|