作者简介: 谢林江, 1993年生, 重庆大学大数据与软件学院硕士研究生 e-mail: 584283862@qq.com
在近红外光谱数据分析中, 全光谱数据具有波长点多、 冗余量大、 共线性关系严重的特点, 导致了部分波长点对建立校正模型没有积极作用, 甚至还会降低模型的预测能力。 波长选择被证明是有效避免上述问题的重要方法。 针对近红外光谱的特性, 提出了一种基于直接正交信号校正(DOSC)与蒙特卡罗方法(Monte Carlo, MC)结合的波长选择算法。 与大多数根据波长的“重要性”进行选择的方法不同, MC-DOSC依据波长的“不重要”性进行选择。 波长“不重要”性通过DOSC的权重 w来度量。 首先将 w归一化作为波长被滤除的概率, 以此建立波长选择的概率模型, 并使用蒙特卡罗随机抽样得到 N个波长子集的集合。 在每一次抽样过程中, 用选择的波长点建立PLS模型, 计算相应的交叉验证均方根误差(RMSECV)。 经过 N次随机抽样后, 以RMSECV最小时的PLS模型对应的波长子集作为备选子集。 将备选子集包含的光谱数据作为新的光谱阵, 重复上述过程直到RMSECV不再下降为止。 迭代停止后, 将RMSECV最小的备选子集作为最佳波长子集。 采用玉米数据集和汽油数据集对该算法进行测试, 同时与蒙特卡罗无信息变量消除法(MCUVE)、 遗传算法(GA)、 竞争性自适应权重取样法(CARS)三种算法进行比较。 实验结果表明: 该算法能大幅度减少波长点个数, 并且相应的PLS模型的预测能力也提高了。 玉米数据集的实验运行结果, 波长点个数从全光谱的700个减少到15个, 预测集相关系数从0.828 2提高到0.931 4, RMSEP从0.109 8减少到0.071 3。 汽油数据集的实验运行结果, 波长点个数从全光谱的301个减少到31个, 预测集相关系数从0.987 5提高到0.993 9, RMSEP从0.255 5减少到0.178 8。 该算法在2个数据集中的表现均优于对比的三种算法。
In the analysis of near-infrared spectroscopy data, full-spectrum data has the characteristics of multiple wavelength points, large redundancy, and serious collinearity. This leads to some wavelength points that have no positive effect on the establishment of the correction model and even reduce the model's predictive ability. Wavelength selection has proven to be an important method to avoid above problems effectively. Aiming at the characteristics of near-infrared spectroscopy, a wavelength selection algorithm based on the combination of Direct Orthogonal Signal Correction (DOSC) and Monte Carlo (MC) is proposed. Unlike most methods of selecting wavelength according to its “importance”, MC-DOSC selects wavelength according to its “unimportance”. The “unimportance” of wavelength is measured by the weight W of DOSC. Specifically, first, normalize was the probability of wavelength being filtered to establish the probability model of wavelength selection, and Monte Carlo random sampling is used to obtain the set of N wavelength subsets. The selected wavelength point is used to establish a PLS model in each sampling process, and the corresponding cross-validation root mean square error (RMSECV) is calculated. After N times of random sampling, the wavelength subset corresponding to the PLS model with minimum RMSECV is selected as the candidate subset. The spectral data contained in the candidate subset is used as a new spectral matrix, and the above process is repeated until the RMSECV no longer drops. After the iteration stops, the candidate subset with the smallest RMSECV is taken as the best wavelength subset. And compared with the three algorithms of Monte Carlo Uninformative Variable Elimination (MCUVE), Genetic Algorithm (GA) and Competitive Adaptive Weight Sampling (CARS). Experimental results show that the algorithm can greatly reduce the number of wavelength points, and the prediction ability of the corresponding PLS model is also improved. In the experimental results of the corn data set, the number of wavelength points is reduced from 700 in the full spectrum to 15. The correlation coefficient of the prediction set is increased from 0.828 2 to 0.931 4, and the RMSEP is reduced from 0.109 8 to 0.071 3. In the experimental results of the gasoline data set, the number of wavelength points was reduced from 301 in the full spectrum to 31. The correlation coefficient of the prediction set was increased from 0.987 5 to 0.993 9, and the RMSEP was reduced from 0.255 to 0.178 8. The performance of this algorithm in the two data sets is better than the three algorithms compared.
近红外光谱分析技术因为其分析速度快、 无损、 无污染和成本低等优点, 在农业、 制药、 石化、 环境和医学等领域有着广泛的应用[1]。 近红外光谱也有波长点多、 谱峰重叠、 吸光强度低、 波长点之间共线性严重等特点。 采用全光谱数据进行分析和建模, 不但会增加模型的运算时间, 也会增加模型的复杂度, 其中部分波长点还会降低模型的预测质量[2]。 选择出有效的波长点参与建模有着重要的实际意义。
为了有效选出合适的波长点, 基于不同原理的波长选择算法先后被提出。 主要有蒙特卡罗无信息变量消除法(Monte Carlo uninformative variable elimination, MCUVE)[3]、 遗传算法(genetic algorithms, GA)[4]、 连续投影算法(successive projections algorithms, SPA)[5]、 协同间隔偏最小二乘法(synergy interval PLS, SiPLS)[6]、 向后间隔偏最小二乘法(backward interval partial least square, B-iPLS)[7]、 变量迭代空间收缩算法(variable iterative space shrinkage approach, VISSA)[8]、 竞争性自适应权重取样法(competitive adaptive reweighted sampling, CARS)[9]、 随机蛙跳(random frog, RF)[10]和最小绝对收缩和选择算法(least absolute shrinkage and selection operator, LASSO)等。 基于PLS回归系数为波长重要性指标进行波长筛选是一类常用方法[11, 12, 13], 如MCUVE, VISSA, CARS等。 但是, 基于回归系数“ 重要性” 进行选择的方法存在两个问题: ①由于光谱容易受到噪声和仪器测量误差的影响, 回归系数并非总是体现波长“ 重要性” 的真实信息。 ②利用回归系数选择波长有着主因子个数选取的困难, 不同的主因子个数对应的回归系数往往有着较大的不稳定性。
针对上述问题, 提出一种通过滤除“ 不重要” 波长进行选择的新方法。 首先用直接正交信号校正(direct orthogonal signal correction, DOSC)提取光谱中与物质浓度阵无关的信息, 将其权重向量绝对值归一化后作为波长被筛除的概率, 然后用Monte Carlo方法进行迭代, 逐步剔除不重要的波长。 通过玉米和汽油数据集对MC-DOSC进行了验证, 并与MCUVE, GA和CARS三种算法进行了对比, 验证MC-DOSC的有效性。
1.1.1 玉米数据集
玉米数据集包含玉米近红外光谱及其植物油(oil)的含量, 此数据集是80个玉米样本在m5, mp5和mp6三台不同光谱仪采集得到。 实验采用的光谱由mp5光谱仪采样得到。 波长采集范围为1 100~2 498 nm, 采集间隔为2 nm, 共700个波长点。 使用duplex方法将样本分成60个训练集样本和20个验证集样本。 数据集可从http://www.eigenvector.com/data下载。
1.1.2 汽油数据集
汽油(gasoline)数据集[14]包含汽油的近红外光谱及其辛烷值(octane)。 此数据集含有60个样本, 波长采集范围为900~1 700 nm, 采集间隔为2 nm, 由于其前100个波长(900~1 100 nm)几乎不携带有效信息, 故提前将其删除。 使用duplex方法将样本分成45个训练集样本和15个验证集样本。
正交信号校正方法(OSC)通常用于光谱预处理, 核心原理是将光谱阵X和浓度阵Y进行正交, 扣除光谱中与浓度无关的信息。 当光谱和浓度的相关性不大或者光谱中背景噪声太大时, 使用OSC方法可以有效减少PLS模型的主因子个数, 降低模型的复杂度, 增强模型的稳健性以及预测能力。
根据扣除方式的不同, 衍生了多种OSC算法, 包括Wold-OSC、 DO(direct orthogonal)、 Fearn-OSC、 O-PLS(orthogonal projects to latent structure)、 DOSC等。 大部分OSC算法, 需要选择主因子个数, 然后通过迭代逐步扣除。 而DOSC算法可以只用一个主因子扣除光谱中与浓度无关的信息, 避免了主因子个数选择的问题[15]。 因此, 采用DOSC提取波长不重要的度量信息。
DOSC首先提取浓度阵Y在光谱阵X所张开的线性空间的投影M, 如图1所示
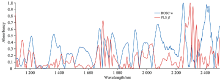 | 图1 DOSC权重向量和PLS回归系数对比, 其中w和β 来源于玉米数据集Fig.1 The comparison of PLS regression coefficients and DOSC weights, where w and β come from the corn data set |
计算X在M的正交补空间的投影Z, 见式(2)
再对ZZT进行主成分分析, 提取前k个需正交处理的主成分得分矩阵T, 再计算权重矩阵W, 见式(3)
得到权重矩阵W。 由DOSC只需一个主因子可知, 仅需取W中第一个权重向量w来度量波长的“ 不重要” 性, 与PLS利用回归系数β 度量波长的重要性有互补关系。 将DOSC权重向量w与PLS回归系数β 作对比, 如图1所示。 可以看出, DOSC的权重向量和PLS的回归系数具有明显的互补关系。
将DOSC的权重向量w作为度量波长“ 不重要” 性的依据, 并以此选择波长。 由于近红外光谱受到吸光度低、 谱峰重叠和噪声等因素的影响[16], 严格根据DOSC权重向量w的绝对值大小进行波长筛选一般不会得到最佳波长点子集。 针对这个问题, 将权重向量w绝对值归一化后作为波长点被滤除的概率, 绝对值越小, 对应的波长点被保留的概率越大。 选择正态随机分布函数进行大量的蒙特卡罗模拟, 得到RMSECV最小时对应的波长点作为备选子集, 再对以上过程进行迭代, 得到一系列备选子集, 然后从中选出RMSECV最小的作为最佳子集。 MC-DOSC波长选择算法的主要步骤如下:
Step1: 将光谱阵X与浓度阵Y进行DOSC, 得到权重向量w;
Step2: 对权重向量w求绝对值并归一化得到相应的概率pj;
Step3: 初始化k=1, 生成正态分布随机向量R~N(0, 1), 将R求绝对值并归一化得到rj;
Step4: 滤除波长点{j|pj> rj, j=1, 2…, n}, 其余波长点用PLS建模, 使用十折交叉验证(10-fold cross-validation)计算RMSECV, 并确定主因子数;
Step5: 当k< N时, k=k+1, 回到Step3, 当k=N时, 进入Step6;
Step6: 在N个RMSECV中选择最小的RMSECV所对应的波长点作为备选子集;
Step7: 将备选子集作为新的光谱阵Xnew代回Step1进行迭代, 直到备选子集波长点个数等于1, 执行Step8;
Step8: 从所有的备选子集中, 选出RMSECV最小的备选子集作为最佳波长子集。
在该算法中, Step5中的蒙特卡罗模拟次数N取500; 最大主因子数由全谱的蒙特卡罗交叉验证(MCCV)确定。 为了提高算法运行效率, 同时尽量保留关键波长, 在第一次迭代时, 进行波长粗筛, 直接剔除掉“ 不重要” 性pj大于δ 的波长点, 为了确定δ , 以0.05为间隔, 取值范围为0到1, 通过RMSECV确定最优值; 在玉米数据集上, δ 取0.5; 在汽油数据集上, δ 取0.6; 之后进行波长精选, 用蒙特卡罗方法滤除波长点。
将MC-DOSC得到的最佳波长子集建立PLS模型, 并同MCUVE, GA和CARS三种方法所建PLS模型进行对比, 以此验证MC-DOSC算法的有效性。 采用预测集相关系数R和预测均方根误差(RMSEP)来评价模型的性能。 所有算法均在Matlab 2015b软件中实现。
2.1.1 玉米数据集
以玉米数据集的MC-DOSC波长选择过程为例, 如图2所示。 图2(a)展示了每一次迭代中滤除“ 不重要” 性较大的波长点这一过程, 第一次筛选直接剪掉“ 不重要” 性大于δ =0.5的波长点, 达到粗选的目的; 然后用蒙特卡罗方法进行细选, 直到波长点不能再减少为止。 从图2(b)可以看出, 随着迭代的不断进行, 备选子集所建模型的RMSECV逐步减小到最小值, 然后在34次迭代后迅速增大。 分析认为RMSECV达到最小值前, 滤除的是干扰波长点或者对模型贡献很小的波长点; 在达到最小值后, 滤除了对模型贡献很大的关键波长点。 将第34次迭代的备选子集作为最佳波长子集。 图2(c)为最佳波长子集所建PLS模型与全光谱所建PLS模型的RMSEP对比图, 由图2(c)可知, 经过MC-DOSC波长筛选后, 模型的预测能力大幅度提高了。
2.1.2 汽油数据集
在汽油数据集中, 波长选择过程与玉米数据集类似, 如图3(a)、 图3(b)所示, 在第16次迭代后, RMSECV达到最小值, 最终选择第16次迭代时对应的波长点建立PLS模型。 从图3(c)可以看出, 相比于全谱的PLS模型, 经过MC-DOSC波长筛选后, 模型的预测能力同样提高了。
为了验证MC-DOSC算法的有效性, 将MCUVE, GA, CARS和MC-DOSC 4种不同方法选择的波长点建立PLS模型, 然后对比不同方法所建模型预测能力的差异, 以验证MC-DOSC算法的有效性。
2.2.1 玉米数据集
4种方法在玉米数据集选择的波段如图4所示, 可以看出, 4种方法均选择了1 700和2 300 nm附近的波长点, 对应着C-H键的伸缩振动区域。 GA, CARS和MC-DOSC几乎都仅选择了1 650~2 498 nm波段的波长点, 此波段对应着C— H键的一级倍频与合频。 说明对于玉米油分含量的预测, 1 650~2 498 nm波段有着关键作用。
从表1可知, 相比于全光谱, 用4种不同方法筛选波长后, 模型的预测能力都有一定程度的提升。 其中MCUVE选择的波长点最多, 预测结果也最差。 这主要是因为, MCUVE滤除了噪声波长点, 保留了不是噪声但对模型没有贡献的波长点。 CARS选择了较少的波长点, 预测结果也较好。 MC-DOSC选择了15个波长点, 略少于CARS。 MC-DOSC预测结果是4种方法中最好的, 这是因为, MC-DOSC滤除了噪声波长点, 也滤除了对模型没有贡献的波长点。 相较于全光谱的PLS模型, 经过MC-DOSC算法筛选波长后, PLS模型的预测能力大幅度提高。 验证相关系数Rp从0.828 2提高到0.931 4, RMSEP从0.109 8减少到0.071 3。
| 表1 不同模型在玉米数据集预测能力的对比 Table 1 Comparison of prediction ability of different models in corn dataset |
2.2.2 汽油数据集
4种方法在汽油数据集选择的波段如图5所示, 可以看出, 4种方法选择的波长点数相差不大, 均选择了1 410 nm附近的波段, 这对应着芳烃和C— H的合频吸收区域。 MCUVE选择的波段较为集中, 几乎没有选择1 450~1 700 nm波段的波长点, 而这个区域是各种C— H基团以及N— H基团、 O— H基团的伸缩振动的一级倍频吸收区域, 因此MCUVE对映的预测误差也最大。 而CARS和MC-DOSC都选择了其他方法没有选择的1 700 nm附近的波段, 这对映着甲基C— H的一级倍频吸收区域。
从表2可知, 尽管MCUVE选择了最多的波长, 但预测结果并不理想。 MC-DOSC选择了最少的波长, 预测结果也是最好的。 相较于全光谱PLS模型, 经过MC-DOSC算法筛选波长后, 验证相关系数Rp从0.987 5提高到0.993 9, RMSEP从0.255 5减小到0.178 8。
| 表2 不同模型在汽油数据集预测能力的对比 Table 2 Comparison of prediction ability of different models in gasoline data sets |
针对近红外光谱的特性与光谱分析存在的问题, 提出一种新的波长选择算法MC-DOSC。 该算法利用直接正交校正(DOSC)得到的权重向量w度量波长的“ 不重要” 性, 再结合蒙特卡罗方法进行波长筛选。 用MCUVE, GA和CARS 在两个数据集上的实验进行了对比, 验证了MC-DOSC算法的有效性。 实验结果表明, MC-DOSC是一种有效的波长选择算法, 具有广泛的应用价值。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|






