作者简介: 卢启鹏, 1964年生, 中国科学院长春光学精密机械与物理研究所研究员 e-mail: luqipeng@126.com
在近红外光谱分析过程中, 单台仪器在不同时间的波长变化及多台仪器间的波长一致与否会对化学计量学定标模型的校正及传递效果产生影响, 上述问题可以统一为波长漂移对定标模型的影响。 以分析小麦粉中粗蛋白含量为例, 首先结合不同谱区光谱数据, 利用偏最小二乘回归(PLSR)方法建立了两个定标模型。 再由计算机生成不同类型、 不同幅度的波长漂移信息, 并叠加至验证集样品光谱中, 使新光谱相对于定标集光谱产生波长漂移信息。 通过考察原定标模型对新光谱的预测与校正情况, 研究了波长漂移对PLSR定标模型的影响。 结果表明: 相对于定标集样品光谱, 验证集光谱中无波长漂移信息时, 模型的预测标准差(RMSEP)不超过0.3%, 预测相关系数不小于0.98; 验证集样品光谱在不同波长处的波长漂移信息为一恒定值时, 模型的RMSEP会随波长漂移幅度的增大而增大, 波长漂移量为-32 cm-1时对应RMSEP为3.69%, 预测相关系数变化不大; 当验证集样品光谱在不同波长处的波长漂移信息随机变化时, 基于长波区光谱所得原始模型的预测结果几乎不受影响; 当含有不同波长漂移信息的一系列样品光谱加入到定标集对长波区PLSR分析模型进行校正时, 校正后模型的RMSEP为0.3%, 几乎不受波长漂移信息的影响, 但模型的回归因子数从3显著增大到8, 其稳健性变弱; 总的来说, 当仪器存在波长漂移且幅度不大时, 模型预测相关系数几乎不受影响, 可通过对预测结果的校正来改善RMSEP, 以保证分析结果的准确性。 该研究为确定仪器设计参数及分析方法的操作规程, 提高近红外光谱分析结果的可靠性提供了实验依据。
Partial least squares regression (PLSR) calibration model will be effect by the wavelength change of a single instrument at a different time and the wavelength consistency of multiple instruments. The process of near-infrared spectroscopy analysis, this problems can be unified as the effect of wavelength drift on chemometric calibration model. In this paper, taking the analysis of crude protein in wheat flour as an example, two calibration models I and II were established by partial least squares regression (PLSR) method within different spectral regions. Different types and amplitudes of wavelength shift information were generated by computer and superimposed into the spectra of the validation set to produce wavelength shift information relative to the spectra of calibration set, the effect of wavelength drift on PLSR calibration model was studied by adding different types and amplitude of wavelength drift information to the spectra of the validation set samples. The results show that the RMSEP of every model is no more than 0.3% and the corresponding Rp is no less than 0.98 when there is no wavelength drift information in the spectra of validation set samples. When the wavelength drift at different wavelengths is constant, the RMSEP increases as the wavelength drift amplitude increases, the RMSEP increases to 3.69% when the wavelength drift is -32 cm-1, and the Rp is almost constant; When the wavelength drift varies randomly at different wavelengths, the prediction results of model II based on long wavelength regions are almost not affected. The model II is corrected by a series of spectra added to the calibration set with different wavelength drift information, the RMSEP of the corrected model is 0.3%, The influence of wavelength drift information on RMSEP has been almost eliminated, but the number of regression factors used to establish corredted model increases significantly from 3 to 8, the robustness of the model varies greatly. In general, the RMSEP can be polished by correcting the prediction results to ensure the accuracy of the analysis results if the amplitude of wavelength drift is slight. This study provides an experimental basis for determining the design instrument parameters and operating procedures to improve the reliability of NIR analysis results.
与传统湿法化学分析手段不同, 近红外光谱分析技术无需化学试剂、 分析速度快、 操作简便、 可多通道同时测量[1], 已被广泛应用于食品、 农业、 烟草、 制药、 化工等行业的品质控制[2, 3, 4, 5, 6], 展现了非常广阔的应用前景。
在获取待测物的近红外光谱过程中, 由于光电、 机械零部件的松动、 老化等原因, 会导致仪器波长发生变化[7]。 同样, 同型号多台仪器之间, 由于零部件加工误差的存在, 波长一致性成为仪器出厂检验的重要指标之一[8]。 仪器波长的变化与不一致性会影响化学计量学分析模型的校正及传递效果[9, 10, 11]。 单台仪器波长变化与多台仪器间波长不一致性可以统一为仪器在不同条件下的波长漂移问题, 利用先前仪器所得光谱建立的校正模型分析波长漂移后所测得的样品光谱时, 会对分析结果产生影响。 因此, 研究波长漂移对定标模型的影响对确定仪器的设计参数及确认仪器的工作状态具有十分重要的意义。
针对以上问题, 以小麦粉为研究对象, 获取其近红外光谱, 利用偏最小二乘回归(partial least square regression, PLSR)算法建立分析小麦粉中粗蛋白干基含量的定标模型。 根据波长漂移数据实际分布区间, 向原始光谱叠加波长漂移信息, 利用先前建立的定标模型, 对叠加波长漂移信息的光谱进行分析预测, 研究波长漂移对定标模型的影响。
收集不同产地的小麦样品70个, 经粉碎机磨碎后, 据GB/T5511— 2008规定的方法测量其粗蛋白质干基含量。
光谱采集使用Nicolet公司的Nexus870型FT-NIR光谱仪, 配备卤钨灯光源、 InGaAs探测器、 镀金积分球及旋转样品池采样部件; 光谱测试环境温度为(25± 2) ℃, 仪器开机预热30 min, 设置光谱扫描范围为4 000~10 000 cm-1, 光谱分辨率为8 cm-1; 以空气为背景, 每30 min更新一次; 样品光谱扫描次数为100。
数据处理程序采用MathWorks公司Matlab7编写, 生成波长漂移信息并叠加至原始光谱中; 针对处理后的光谱数据, 结合光谱仪器自带软件TQ Analyst建立PLSR定标模型。
为了更科学地表达波长漂移信息, 根据某品牌近红外仪器公开数据, 其波长范围为900~1 700 nm, 256像元铟镓砷阵列探测器, 波长校准数据统计结果如表1所示。
| 表1 某型号仪器波长校准结果 Table 1 Statistical results of wavelength calibration of a certain type of instruments |
表1统计结果中, 波长漂移幅度最大值1.22 nm, 在900~1 700 nm波长区间, 对应波数约为8~16 cm-1。 本研究设定的波长漂移量为-32, -24, -16, -8, 8, 16, 24和32 cm-1等8个数据。 这里规定, 当波长漂移量为负时, 吸光度值向短波方向偏移; 当漂移量为正时, 吸光度值向长波方向偏移。 采用两种方法生成波长漂移信息并向原始光谱中叠加, 具体方法如下: (1)针对不同波长漂移量, 分别使原始光谱所有波长下的吸光度值按照相应波长漂移量进行偏移。 (2)首先用计算机分别生成与波长点个数相同的、 均值为0、 方差σ 为波长漂移幅度(8, 16, 24和32 cm-1)的随机数序列, 以相应随机数序列中的随机数作为对应波长下的波长漂移量, 原始光谱对应波长下的吸光度值按照对应波长漂移量所处位置相邻两波长处的吸光度进行线性插值进行确定。
通过以上处理, 可用所得光谱表征原始仪器在对应波长漂移量下获取的一系列小麦粉样品的光谱数据。 为方便数据处理, 光谱数据两端不能处理的吸光度值与原始光谱保持一致, 后续定标过程, 按照“ 掐头去尾” 的方式剔除无偏移处理的光谱数据。
含氢基团在近红外谱区的吸收带一般可分为合频区、 倍频区, 结合铟镓砷探测器光谱响应上限1 700 nm(5 882.35 cm-1)及数据处理过程中使用到的“ 掐头去尾” 操作, 基于短波区9 900~6 000 cm-1、 长波区6 000~4 100 cm-1两光谱区间数据分别建立定标模型。
本研究从所有样品中随机挑选40个作为定标集, 另30个为验证集, 同时为保证验证集样品化学值分布区间在定标集样品化学值分布区间内, 可二次对定标集、 验证集样品进行调整。 利用PLSR方法建立分析小麦粉中粗蛋白干基含量的定标模型, 对进行波长漂移处理后的验证集数据进行分析预测, 研究波长漂移对定标模型的影响。
利用设计的两种方法生成波长漂移信息分别对原始光谱进行处理。 方法(1)叠加32和-32 cm-1波长漂移信息后的两样品光谱及按照方法(2)叠加σ 32 cm-1波长漂移信息后的一样品局部光谱分别如图1(a, b)所示。
 | 图1 叠加不同波长漂移信息的小麦粉近红外光谱Fig.1 NIR spectra of wheat flour with different types of wavelength drift informantion |
图1(a)中, 两样品的原始光谱间的纵坐标吸光度强度差异明显, 这主要是由于光谱中携带的散射信息差异导致; 而两原始光谱分别与各自叠加波长漂移信息后相比, 光谱形状沿横坐标波长点存在明显的偏移。 当参与定标的光谱数据与待预测光谱数据中的波长漂移量存在差异时, 会对预测结果产生影响。
图1(b)中, 由于样品原始光谱中每个波长点处叠加了呈随机分布的波长漂移信息。 叠加的波长漂移信息表现为随机噪声。 与原始光谱相比, 叠加后的光谱虽存在较多噪声, 但整体特征与原始光谱保持一致。
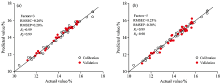
利用PLSR方法, 分别基于短波区9 900~6 000 cm-1、 长波区6 000~4 100 cm-1建立分析粗蛋白干基含量的定标模型Ⅰ 、 定标模型Ⅱ 。 为了得到最优的定标模型, 建立模型Ⅰ 、 模型Ⅱ 时, 组合采用了多元散射校正、 一阶导数光谱两种光谱预处理方法, 最终所得模型结果如图2所示。
图2中, 针对验证集样品, 基于两不同光谱区间数据所得两分析模型的预测相关系数都在0.9以上, RMSEP均不大于0.3%, 具有较好的性能。 不同的是, 模型Ⅱ 比模型Ⅰ 使用较少的因子数, 说明近红外长波段光谱数据中与待分析化学成分含量有关的有效信息能更容易地被PLSR提取解析。
当波长漂移信息叠加到验证集样品的原始光谱后, 分别利用前述两个PLSR定标模型进行预测分析, 结果如表2所示。
| 表2 对叠加不同波长漂移信息光谱的预测结果 Table 2 Prediction results based on the spectra with different types of wavelength drift information |
表2中, 从预测结果来看, 模型的RMSEP相差较大, 说明波长漂移信息会使PLSR模型预测值与参考值产生偏差, 但考虑到此时预测相关系数较大, 均不低于0.97, 预测值与参考值间的偏差存在通过调整回归方程的常数项进行校正的可能性, 进而改善RMSEP值, 在一定程度上消除波长漂移带来的影响。
待分析样品光谱中不同波长处的波长漂移量恒定时, 基于长波区数据所得模型的预测结果普遍优于基于短波区所得模型的预测结果, 且基于相同波段所得模型对叠加波长漂移信息光谱的预测能力随波长漂移幅度的增大而减弱。 波长偏移量为-32 cm-1时, 对应模型的RMSEP最大为3.69%, 且定标相关系数降至0.97; 波长偏移量为8 cm-1时, 对应模型Ⅱ 的RMSEP最小为0.51%。
待分析样品光谱中不同波长处的波长漂移量随机分布时, 模型Ⅰ 的预测能力随随机数序列方差的增大而减弱, 但预测相关系数同样不低于0.97。 进一步分析发现, 建立模型Ⅱ 时, 仅使用了前3个成分进行回归, 利用模型Ⅱ 分析待测样品光谱数枯时, 与化学成分无关的波长漂移信息基本不影响前3个成分的计算, 预测结果也几乎不受影响。
为了进一步研究PLSR模型处理叠加波长漂移信息光谱数据时的可校正性, 需重新划分光谱数据集, 并利用叠加不同类型波长漂移信息的样品光谱混合建模。 原始30个验证集样品被平均分为5组, 利用模型Ⅱ 预测相关系数不低于0.99时对应的5种波长漂移信息8, -8, -24, σ 8及σ 16 cm-1, 分别叠加到上述5组光谱数据中。 并分别从每组选取2个样品共计10个样品加入定标集, 相应从原始40个定标集样品中随机出10个样品为加入验定集, 最终组成包含样品数分别为40和30的定标集与验证集, 利用PLSR方法建立蛋白质干基分析模型, 结果如图3所示。
 | 图3 基于不同类型波长漂移信息光谱定标结果Fig.3 Calibration results based on the spectra with different types of wavelength drift |
明显地, 图3所示模型与模型Ⅱ 相比, 除因子数从3增加到8之外, 其他参数基本没有变化, 说明当波长偏移幅度不超过24 cm-1情况下, 通过加入含有波长漂移信息的样品数据进行定标, 可以对原始模型进行校正, 且校正后的模型的预测精度基本不受波长漂移信息的影响, 但参与PLSR模型建立的最优因子数大幅度增加, 模型的稳健性降低。
近红外光谱仪器在研发和使用过程中, 无论是不同仪器之间, 还是同一仪器的不同状态, 仪器的波长参数很难保证恒定, 这会导致光谱吸收强度与波长间的对应关系发生变化, 进而对模型的分析结果、 校正及传递效果产生影响。 仪器厂家通过严格的出厂标准检验及在仪器中内置波长校准单元来保证波长的准确性和重复性, 但波长漂移具有系统性的原因, 针对不同的波段, 不同的分析对象及分析要求, 对仪器波长的一致性要求也是有差异的。
在本研究使用的数据范围内, 光谱中叠加的波长漂移信息对所得模型的RMSEP影响显著, 但由于预测相关系数较大, 存在通过对预测结果的校正在一定程度消除波长漂移对定标模型影响的可能性; 在长波段, 验证集样品光谱数据在不同波长处叠加随机波长漂移信息后, 由于建立PLSR模型时用到的前3个因子几乎不包含波长漂移信息, 以致PLSR模型的预测能力基本不受波长漂移信息影响; 当包含不同类型波长漂移信息的样品光谱数据加入到定标集对PLSR分析模型校正时, 建立新模型用到的因子数显著增大, 模型的稳健性降低。 本研究为确定仪器的出厂参数的和制定仪器的操作规程, 提高近红外光谱分析结果的可靠性提供了实验依据。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|