引用本文
孙学辉, 赵冰, 骆震, 孙培健, 彭斌, 聂聪, 邵学广. 近红外光谱判别分析滤波器的设计与应用[J]. 光谱学与光谱分析, 2022,42(2): 399-404.
SUN Xue-hui, ZHAO Bing, LUO Zhen, SUN Pei-jian, PENG Bin, NIE Cong, SHAO Xue-guang. Design and Application of the Discrimination Filter for Near-Infrared Spectroscopic Analysis[J]. Spectroscopy and Spectral Analysis, 2022,42(2): 399-404.
Doi:10.3964/j.issn.1000-0593(2022)02-0399-06  
Permissions
Copyright©2022, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
近红外光谱判别分析滤波器的设计与应用
孙学辉1, 赵冰2, 骆震2, 孙培健1, 彭斌1, 聂聪1,*, 邵学广3,*
1.中国烟草总公司郑州烟草研究院, 河南 郑州 450001
2.河南中烟工业有限责任公司, 河南 郑州 450000
3.南开大学化学学院分析科学研究中心, 天津 300071
*通讯作者 e-mail: congnie@aliyun.com; xshao@nankai.edu.cn

作者简介: 孙学辉, 女, 1981年生, 中国烟草总公司郑州烟草研究院高级工程师 e-mail: xuehui_sun1234@aliyun.com

收稿日期: 2020-09-01 修回日期: 2021-01-09 接受日期: 2021-01-09
基金: 中国烟草总公司重点实验室项目(110201803001), 国家自然科学基金项目(21775076)资助
摘要

近红外光谱(NIRS)在定量和判别分析中已得到广泛应用, 化学计量学在其中发挥了重要作用, 但仍需要建立基于新原理的方法, 简化数据处理和建模过程, 使近红外光谱分析更加方便、 更加快速。 多元光学计算(MOC)技术通过设计合适的光学滤波器可以在光谱测量的同时, 根据光谱的整体形状得到定性定量结果。 作为一种新的测量和计算方式, 近年来在光谱分析领域逐渐得到应用。 基于多元光学计算的原理, 基于主成分分析和Fisher判别准则设计了近红外光谱的判别滤波器, 将近红外光谱投影到二维空间, 并在二维空间中计算每一类样品的置信椭圆作为模型进行判别分析。 预测样本在二维空间的投影与模型的距离可以作为判别参数, 判别值小于等于1时预测样品与模型样品判别为同一类别, 否则判别为不同类别, 且距离越大, 差异性越大。 采用460个不同部位的烟叶样品和73个不同生产厂家的药品对所建立的方法进行了测试, 表明了方法的准确性。 对于三类不同部位烟叶样品和四类不同厂家生产的药品, 预测结果的真阳性率可以达到90%以上(除上部烟叶样品外), 药品的真阳性率高达95%以上。 但烟叶样品的假阳性率仍有些偏高, 对于光谱极为相似的实际生产样品结果仍属可接受范围。 所建立的方法可推广到其他应用领域, 广泛用于基于近红外光谱的质量控制、 产品检测、 生产一致性监控等。

关键词: 近红外光谱; 化学计量学; 滤波器设计; 置信椭圆; 判别分析
中图分类号:O657.3 文献标志码:A
Design and Application of the Discrimination Filter for Near-Infrared Spectroscopic Analysis
SUN Xue-hui1, ZHAO Bing2, LUO Zhen2, SUN Pei-jian1, PENG Bin1, NIE Cong1,*, SHAO Xue-guang3,*
1. Zhengzhou Tobacco Research Institute of China National Tobacco Corporation, Zhengzhou 450001, China
2. China Tobacco Henan Industry Co., Ltd., Zhengzhou 450000, China
3. Research Center for Analytical Sciences, College of Chemistry, Nankai University, Tianjin 300071, China
*Corresponding authors
Abstract

Chemometrics has been widely applied in near-infrared (NIR) spectroscopic analysis for quantitative detection and discrimination. However, new methods are still needed to simplify data processing and modeling to speed up the analysis and improve the convenience in practical uses. As a new type of technique for spectroscopic measurement and computation, the multivariate optical computing (MOC) technique is employed in spectroscopic analysis. The technique uses multivariate information in the spectrum to achieve quantitative computation and discrimination through the designed filters. In this work, the filters for discrimination analysis of near-infrared spectroscopy was designed based on principal component analysis (PCA) and Fisher's discrimination criterion. The spectra of the calibration samples can be projected into a two-dimensional space by the two filters to achieve an optimized classification, and a confidence ellipse can be obtained for each class of the samples. The ellipse can be used as a model for the discriminating the prediction samples. The distance of a prediction sample to the model is a good measurement of its classification. The samples with a distance less or equal to 1 are classified into the same class of the model, but those with a distance larger than 1 is excluded from the class, and the larger the distance, the bigger the dissimilarity. The proposed method was tested with the NIR spectra of 460 samples of tobacco leaf in three different parts of the plant and 73 samples of the medicinal capsules (amoxicillin granules) produced by four producers. The true positive rate can be higher than 90%, except for the tobacco samples and even higher than 95% for the capsule samples. However, the false-positive rate of the tobacco samples is still not so satisfactory due to the similarity of the NIR spectra. Using near infrared spectroscopy, the proposed method may provide a good technique for quality control, product detection and production monitoring in different fields.

Keyword: Near infrared spectroscopy; Chemometrics; Filter design; Confidence ellipse; Discrimination analysis
引言

由于近红外光谱(NIRS)技术可用于快速、 无损、 在线/在位分析等, 近年来在许多领域的科学研究及各行业的应用研究得到快速发展[1]。 但是, 由于近红外光谱在光谱分辨率、 信号强度、 谱峰重叠等方面的不足, 化学计量学方法是很多应用的关键。 所涉及的化学计量学方法可归纳为与定量和定性建模相关的两大类方法, 前者建立光谱与含量之间的定量模型, 后者包括基于光谱数据的聚类分析及判别模型的建立。 为了建立准确、 稳定、 实用的模型, 在信号处理、 变量选择、 建模方法等方面开展了大量的研究工作[2, 3]。 信号处理一般采用MSC、 SNV进行散射校正, 采用导数光谱技术校正或扣除变动的背景。 由于小波变换在近似导数计算时同时具有平滑效果, 并且可以进行任意阶导数的计算, 在近红外光谱的导数计算中得到了广泛应用, 特别是在高阶导数计算方面发挥了积极作用[4, 5, 6]。 变量选择对于精简和改善近红外光谱模型具有显著作用, 提出并建立了大量变量选择方法用于模型性能的提高[7], 其中基于统计学的变量评价方法得到了较好的应用[8, 9, 10]。 在建模方法研究方面, 除针对定量模型的各种探索外[11, 12], 针对聚类分析和判别分析的方法也得到了广泛研究[13, 14, 15]。 化学计量学方法的发展与进步为近红外光谱在各领域和行业中的应用提供了技术支撑与保障。

近年来, 以多元光学元件(MOE)为滤波器的多元光学计算(MOC)技术在光谱仪器的设计中得到应用与发展。 多元光学计算的基本思想是20世纪70年代提出的“ 光学信号处理(OSP)” , 即采用光谱的整体形状进行定性定量分析, 并且在光学空间中实现计算[16, 17]。 多元光学计算作为一种新的测量和计算方式, 已在光谱分析中得到应用, 如浮游植物的判别[18]、 血迹识别[19]、 高温高压下的原油检测[20]等。 基于多元光学计算的原理, 可以通过滤波器的设计实现近红外光谱的快速分析, 即将光谱数据通过滤波器的“ 过滤(投影)” 直接得到分析结果。 在以往研究工作中, 曾分别实现了用于定量和判别分析的数字滤波器。 通过优化小波函数的组合得到滤波器, 将滤波器作用于近红外光谱得到小波系数, 然后建立小波系数与分析物含量之间的多元线性回归模型, 使用由4个Symlet小波函数与多元线性回归模型的系数结合构造的滤波器实现了对谷物、 小麦和血液三种样品的定量分析, 滤波器的预测效果明显优于传统的PLS模型, 并且建模时不再需要背景扣除、 变量选择等光谱处理[21]。 将主成分分析与线性判别分析的结合建立了基于主成分投影与判别函数融合的滤波器, 实现了不同类别药品的聚类和判别分析[22]。

本工作在构建基于Fisher准则的线性判别滤波器的基础上, 提出了一种基于置信椭圆的判别方法, 将两个正交的滤波器直接作用于近红外光谱, 得到二维空间的数据点。 通过校正集样品的数据点得到置信椭圆作为模型, 通过待测样品的数据点与置信椭圆的相对位置(内、 外)及距离判别待测样品与校正集的类属关系和相似性评价。 通过不同部位烟叶样品的判别和不同厂家药品一致性的判别证明了该方法可提取不同样品在近红外光谱中的微弱差异, 为基于近红外光谱的快速判别分析提供了一种良好算法。

1 实验部分
1.1 样品

研究中采用了两组样品的近红外光谱。 第一组是460个烟叶样品, 由上(X)、 中(C)、 下(B)三个不同部位的烟叶构成, 分别56, 246和158个样品, 制备成烟末(60目)进行光谱扫描。 第二组是阿莫西林颗粒剂, 共73个样品, 分为A(17个)、 B(20个)、 C(18个)、 D(18个)四类, A和B为同一公司不同厂家生产, 且已知B类的配方与A类有所区别, C和D为同一公司不同厂家生产。

1.2 光谱测量

光谱的测量采用漫反射方式。 烟叶样品使用的是AntarisTM Ⅱ 傅里叶变换近红外光谱仪(热电, 美国), 药品光谱的测量仪器是MPA傅里叶变换近红外光谱仪(布鲁克, 德国)。 光谱测量的光谱分辨率为8 cm-1, 波数范围分别是3 999.6~10 001.0和3 999.8~11 995.3 cm-1, 数据点之间的波数间隔约为3.86 cm-1。 每个烟叶样品测量一条光谱, 但药品光谱的测量中每个样品进行了6次重复。

1.3 数据集

计算中, 两组光谱数据分别使用了波数在3 999.6~10 001.0和3 999.8~9 997.5 cm-1的光谱数据, 分别为1 557和1 556个数据点。 校正集和预测集的划分按照样品的测试顺序(随机)间隔取样, 即奇数序号样品为校正集, 偶数序号样品为预测集。 因此, 除药品A类校正集样品数为9, 预测集样品数为8外, 其他各类别的校正集与预测集样品数均相同。

2 计算原理与步骤
2.1 原理与算法

工作目标是定义一个判别参数, 根据参数的数值对样本的类别进行判别。 首先需要根据校正集的近红外光谱进行聚类分析, 然后建立每一类样本的判别模型, 再分别使用每一类的模型对待测样本进行判别。 首先将校正集样本的近红外光谱投影到具有最佳分类效果的二维空间, 然后在二维空间中计算每类样本的置信椭圆, 最后利用置信椭圆作为模型对待测样本进行判别。 所涉及的计算主要是滤波器的构建和置信椭圆模型的建立与运用。

滤波器的构建采用了Fisher准则, 即通过式(1)的最大化确定判别向量d,

dTkBdkdTkWdk(1)

式(1)中B和W分别是类间方差和类内总方差, 计算时采用了光谱在主成分空间的得分(T), dk是判别向量。

根据主成分分析的模型, 得分(T)可由光谱X和载荷(P)得到, 见式(2)

T=XP(2)

因此, 光谱在二维投影空间的数值, 见式(3)

K=XPd(3)

将Pd记为F, 即为将光谱投影到二维空间的滤波器, 见式(4)

K=XF(4)

根据每一类校正集样本的Ki值(i=1, …, N, N为类别数)可以计算每一类的置信椭圆(即模型), 记为(x0, y0, a, b, θ ), 即椭圆的中心、 长短轴及主轴的方向。 判别时, 根据式(3)计算光谱x的判别值k(k1, k2), 即在二维空间中待测样本的位置, 然后计算与模型(置信椭圆)的距离v, 即判别参数。 v< 1, > 1或=1分别表示待测样本的投影点在椭圆内、 外或落在椭圆上, 即v≤ 1时判别为与模型类型相同, 否则判别为不同, 并且数值越大, 表示差异越大。

2.2 计算过程

对于已知N类样品的校正集光谱X和待预测样本的光谱Xp, 计算过程为:

(1)对X主成分分析, 得到得分T与载荷P。

(2)由得分T计算B和W并根据式(1)计算判别向量d。 为了方便后续的判别分析, 采用两个正交的判别向量, 必要时可采用多个以增加判别的维度。

(3)由P和d计算滤波器F。

(4)根据式(4)计算校正集光谱的投影K(k1, k2)。

(5)根据每一类样本的Ki得到每一类样品的判别模型(x0, y0, a, b, θ )。

(6)对于每一个预测样本, 由光谱x和滤波器F计算投影k(k1, k2), 再利用判别模型得到判别参数值v。 根据v的数值得到判别结果。

3 结果与讨论
3.1 数据处理与常用方法的判别结果

图1(a)和(b)分别是烟叶样品和药品的近红外光谱图, 其中蓝色为校正集光谱, 红色是预测集光谱。 首先, 从光谱很难直接看出不同类别样品之间的差异, 直接采用光谱进行聚类和判别分析十分困难。 其次, 两组样品的光谱图中均有较大的背景且样品之间的差异较大。 因此, 必须依靠数据处理和化学计量学方法进行信息提取, 才能突出光谱之间的差异, 实现聚类和判别。 为了尽量减少信号处理步骤, 充分利用判别滤波器实现样品光谱差异的提取, 只对光谱进行了导数计算。 图2(a)和(b)分别是采用Savitzky-Golay(SG)方法计算的一阶导数光谱, 计算中多项式阶数和窗口宽度分别设置为2和17。 导数光谱图使变动的背景得到了校正, 但依然难以看出不同类别样品之间的光谱差异。

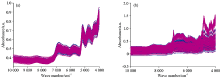图1 烟叶样品(a)和药品(b)的近红外光谱
蓝色: 校正集; 红色: 预测集Fig.1 NIR spectra of tobacco leaves (a) and medicine capsules (b)
Blue: Calibration set; Red: Prediction set

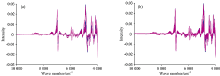图2 烟叶样品(a)和药品(b)的一阶导数光谱
蓝色: 校正集; 红色: 预测集Fig.2 Derivative spectra of tobacoo leaves (a) and medicine capsules (b)
Blue: Calibration set; Red: Prediction set

为了进一步考察不同类别样品光谱之间的差异, 对校正集光谱的导数光谱进行了主成分分析。 图3(a, b)分别为烟叶、 药品两组数据的分析结果, 即样品在PC1和PC2空间的分布情况, 两个主成分所解释的方差率标注在各自的坐标轴上。 从方差解释率(87.23%和99.07%)可以看出, 两个主成分解释了绝大部分光谱的方差, 但聚类效果很不理想。 图3(a)中上、 中、 下三类烟叶的置信椭圆(99%)大部分重叠, 基本无法区分, 图3(b)中的药品只能区分不同公司的产品, 对于配方差异的区分能力有限, 对于配方相同的不同厂家的产品基本没有区分能力。

图3 主成分分析聚类结果(在PC1和PC2空间中的分布)
(a): 烟叶样品; (b): 药品Fig.3 Clustering in principal component space (the distribution in PC1 and PC2 space)
(a): Tobacco leaves; (b): Medicine capsules

3.2 滤波器的构建与判别结果

为了使校正集的样品得到最优的聚类效果, 按照本方法, 即计算过程中的第(1)— (3)步, 分别利用烟叶与药品两组样品校正集的近红外光谱计算了滤波器F, 如图4(a, b)所示。 可以看出, 对于组成较为复杂的烟叶样品, 整个光谱区间的光谱变量对聚类都有作用, 甚至是8 000 cm-1以上的高倍频变量, 而对于化学组成相对较为简单的药品, 对聚类具有较大作用的波数变量主要集中在CH和OH的倍频和合频区。

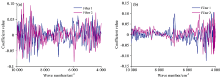图4 烟叶样品(a)和药品(b)近红外光谱的判别滤波器Fig.4 Descrimination filters for the tobacoo leaves (a) and the medicine capsules (b)

得到滤波之后, 根据计算过程的第(4)步即可计算校正集光谱的投影值, 将两个滤波器直接作用于预测光谱即可得到预测集样品在二维空间的位置。 图5绘制了校正集和预测及样品的近红外光谱经滤波器投影在二维空间的分布情况, 图中的置信椭圆根据校正集光谱的投影值得到, 即计算过程的第(5)步。 首先可以看出, 与主成分分析的结果相比较, 各类样品的聚类情况得到了很大程度的改善。 图5(a)中上部烟叶与中、 下部烟叶得到了很好的区分, 中部烟叶与下部烟叶之间也得到了一定程度的分离。 图5(b), 两个公司的产品相距很远, 对于配方有一定的差异的A和 B两类也基本得到了完全分离。 从图5(b)中的局部放大图可以看出, 即使对于同一公司两个厂家的产品(C和D), 也得到了较好的分离。 尽管两个置信椭圆还有部分重叠, 只有极少数的几个数据点存在交叉。

图5 二维空间投影图
(a): 烟叶样品; (b): 药品, 虚线内为局部放大图, 空心点为校正集样品, 实心点为预测集样品Fig.5 Projection in the two-dimensional space of the filters
(a): Tobacoo leaves; (b): Medicine capsules; The insets circled by the dot-line show the enlarged graphs. The calibration and prediction samples are plotted by blind and solid points, respectively

利用图5中的置信椭圆(模型)和预测样品的投影值即可根据计算过程的第(6)步计算每个预测样品的别参数值v, 并利用v值进行判别。 当v值小于等于1时判别为与模型同类, 否则判别为不同。 表1列出来两组数据预测集样品中各类样品的数目及判别的真阳性率(TP)和假阳性率(FP), 前者是某类样品判别正确的百分数, 后者是将不属于本类的样品错误地判别为本类的百分数。 从TP参数看, 基本都达到了很好的效果, 上部烟叶样品的TP值偏低可能是由于此类的样品数较少, 模型的代表性不足。 从FP参数看, 药品的判别结果非常满意, 只有几条光谱(每个样品6条光谱)被错误判别, 但中部和下部烟叶样品的判别结果稍差。 从图3中主成分分析的结果可以看出, 烟叶样品的近红外光谱差异很小, 另外, 烟叶样品是生产过程中的实际样品, 此结果已达到可接受的水平。

表1 烟叶样品和胶囊颗粒剂样品的判别结果 Table 1 Discrimination results for the prediction samples of tobacco leaf and medicinal capsule
4 结论

基于多元光学计算的思路, 提出并建立了一种设计近红外光谱判别分析滤波器的方法和基于置信椭圆的判别参数计算方法。 采用所建立的滤波器可以直接从近红外光谱得到具有最优聚类效果的二维空间投影, 且基于校正集光谱的投影可以得到类别的判别模型(置信椭圆)。 利用预测集的光谱和滤波器可以计算预测光谱的投影值并计算出预测光谱与模型的距离, 即判别参数值。 根据判别值(> 1, < 1, =1)可以方便地对预测集光谱进行判别。 将所建立的方法应用于烟叶样品的部位判别和药品的生产厂家判别, 除个别类别的准确性仍有待提高外, 模型的判别准确率可达到90%以上, 而且计算方便, 判别依据明确。 相对于常用的PCA方法, 判别结果的准确性有明显提高。 所建立的方法有望在基于近红外光谱的判别分析中推广应用, 用于质量控制、 产品检测、 生产一致性监控等的快速分析。

参考文献
[1] Moros J, Garrigues S, de la Guardia M. V Trends in Analytical Chemistry, 2010, 29(7): 578. [本文引用:1]
[2] Pasquini C. Analytica Chimica Acta, 2018, 1026: 8. [本文引用:1]
[3] Shao X G, Bian X H, Liu J J, et al. Analytical Methods, 2010, 2(11): 1662. [本文引用:1]
[4] Shao X G, Leung A K M, Chau F T. Accounts of Chemical Research, 2003, 36(4): 276. [本文引用:1]
[5] Shao X G, Ma C X. Chemometrics and Intelligent Laboratory Systems, 2003, 69(1-2): 157. [本文引用:1]
[6] Shao X G, Cui X Y, Wang M, et al. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2019, 213: 83. [本文引用:1]
[7] Zou X B, Zhao J W, Povey M J W, et al. Analytica Chimica Acta, 2010, 667(1-2): 14. [本文引用:1]
[8] Cai W S, Li Y K, Shao X G. Chemometrics and Intelligent Laboratory Systems, 2008, 90(2): 188. [本文引用:1]
[9] Xu H, Liu Z C, Cai W S, et al. Chemometrics and Intelligent Laboratory Systems, 2009, 97(2): 189. [本文引用:1]
[10] Zhang J, Cui X Y, Cai W S, et al. Science China-Chemistry, 2019, 62(2): 271. [本文引用:1]
[11] Li Y K, Shao X G, Cai W S. Talanta, 2007, 72(1): 217. [本文引用:1]
[12] Jing M, Cai W S, Shao X G. Chemometrics and Intelligent Laboratory Systems, 2010, 100(1): 22. [本文引用:1]
[13] Shan R F, Mao Z Y, Yin L H, et al. Analytical Methods, 2014, 6(13): 4692. [本文引用:1]
[14] Mancini M, Taavitsainen V M, Toscano G. Journal of Chemometrics, 2019, 33(7): e3145. [本文引用:1]
[15] Band ara D, Hirshfield L, Velipasalar S. Journal of Near Infrared Spectroscopy, 2019, 27(3): 206. [本文引用:1]
[16] Bialkowski S E. Analytical Chemistry, 1986, 58: 2561. [本文引用:1]
[17] Nelson M P, Aust J F, Dobrowolski J A, et al. Analytical Chemistry, 1998, 70(1): 73. [本文引用:1]
[18] Faulkner S T, Rekully C M, Lachenmyer E M, et al. Applied Spectroscopy, 2019, 73(3): 304. [本文引用:1]
[19] Brooke H, Baranowski M R, McCutcheon J N, et al. Analytical Chemistry, 2010, 82(20): 8427. [本文引用:1]
[20] Jones C M, Price J, Dai B, et al. Analytical Chemistry, 2019, 91(24): 15617. [本文引用:1]
[21] Li X Y, Xu Z H, Cai W S, et al. Analytica Chimica Acta, 2015, 880: 26. [本文引用:1]
[22] Liu Y, Cai W S, Shao X G. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 22. [本文引用:1]