引用本文
李妍妍, 罗海军, 罗霞, 范鑫燕, 覃睿. 近红外光谱的阵列扫描式灵敏度法探测颅脑血肿[J]. 光谱学与光谱分析, 2022,42(2): 392-398.
LI Yan-yan, LUO Hai-jun, LUO Xia, FAN Xin-yan, QIN Rui. Detection of Craniocerebral Hematoma by Array Scanning Sensitivity Based on Near Infrared Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2022,42(2): 392-398.
Doi:10.3964/j.issn.1000-0593(2022)02-0392-07  
Permissions
Copyright©2022, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
近红外光谱的阵列扫描式灵敏度法探测颅脑血肿
李妍妍1,2, 罗海军1,2,*, 罗霞1,2, 范鑫燕1,2, 覃睿1,2
1.重庆师范大学物理与电子工程学院, 重庆 401331
2.重庆师范大学光电功能材料重庆市重点实验室, 重庆 401331
*通讯作者 e-mail: luohaijun@cqnu.edu.cn

作者简介: 李妍妍, 1998年生, 重庆师范大学光电功能材料重庆市重点实验室硕士研究生 e-mail: 877176124@qq.com

收稿日期: 2020-12-02 修回日期: 2021-02-23 接受日期: 2021-02-23
基金: 国家自然科学基金项目(51507023), 重庆市自然科学基金(面上项目)(cstc2020jcyj-msxmX0726), 重庆市教委科学技术研究项目(KJ1703063), 重庆市研究生科研创新项目(CYS19298), 重庆师范大学研究生科研创新项目(YKC20027)资助
摘要

利用近红外光谱技术对脑组织进行检测实现脑血肿的定位一直以来都是无损光学诊断的研究热点。 为了实现开放式全方位的精准探测, 基于功能性近红外光谱技术提出一种新的方法—阵列扫描式灵敏度法, 即建立全方位阵列探测器, 通过单边阵列式扫描检测来获取不同探测位置的光通量, 计算每个探测器的探测灵敏度, 就能得到全方位的探测信息。 首先, 建立单层有限元模型, 设置光学参数、 光源、 探测位置及边界条件, 将仿真结果与蒙特卡洛的运行结果进行对比, 验证有限元模型条件设置的准确性。 其次, 根据人脑组织结构建立脑部模型, 在模型中插入血肿, 选择波长为850 nm的近红外光作为光源, 设置该波长下各层生物组织的光学参数, 模拟光子在正常脑组织与含血肿脑组织中的传播, 在距光源不同位置的探测器处检测到多组光通量数据, 处理数据后发现有限元仿真软件在图像、 数据方面反映了血肿对光的传播有极大影响。 为研究探测到的光通量信息与血肿位置之间的关系, 基于近红外光谱技术采用阵列扫描式灵敏度法分别改变组织内血肿的方位、 横向位置与纵向深度, 在距光源不同的探测位置处检测到多组光通量数据, 处理数据后建立血肿位置与对应探测灵敏度之间的关系图进行分析。 结果显示采用阵列扫描式灵敏度法, 近红外光谱技术能准确探测血肿的方位信息与横向信息, 且血肿位于源—探测距离中间时, 探测效果最佳, 而纵向深度只影响光子穿过较深层组织的概率, 位置越深, 光子的穿过率越小, 探测灵敏度越小。 由此得出, 基于阵列扫描式灵敏度法可以实现颅脑组织内一定深度处血肿的快速准确定位, 为近红外光谱技术的光学成像、 检测组织内部肿瘤等提供了新思路和有效参考。

关键词: 阵列扫描式灵敏度; 近红外光谱技术; 脑血肿检测; 有限元法
中图分类号:Q63 文献标志码:A
Detection of Craniocerebral Hematoma by Array Scanning Sensitivity Based on Near Infrared Spectroscopy
LI Yan-yan1,2, LUO Hai-jun1,2,*, LUO Xia1,2, FAN Xin-yan1,2, QIN Rui1,2
1. College of Physics and Electronic Engineering, Chongqing Normal University, Chongqing 401331, China
2. College of Physics and Electronic Engineering, Chongqing Key Laboratory of Optoelectronic Functional Materials, Chongqing 401331, China
*Corresponding author
Abstract

The localization of brain hematoma by using functional near-infrared Spectroscopy has always been a research hotspot in the field of nondestructive optical diagnosis. To achieve open and all-around accurate detection, this paper proposes a new method based on functional near-infrared spectroscopy, the Array scanning sensitivity method. Namely to establish an omni-directional array detector, unilateral array scanning tests to get the fluence rate of different probe locations. By calculating the detection sensitivity, we can get a full range of detection information. Firstly, establish the monolayer finite element model, set optical parameters, light source, detection position and boundary conditions. The simulation results are compared with Monte Carlo to verify the accuracy of the conditions. Secondly, build a brain model with hematoma based on the structure of the brain, the light source selects near-infrared light with a wavelength of 850 nm, the optical parameters of biological tissue at this wavelength are set, simulate the propagation of photons in normal brain tissue and brain tissue with hematoma, and multiple sets of luminous flux data are detected at different locations. After processing the data, it is found that the finite element simulation software can reflect the significant influence of hematoma on the transmission of light in images and data. To study the relationship between luminous flux and the location of the hematoma, the azimuth, horizontal position and depth of the hematoma were changed respectively. Multiple sets of luminous flux data were also detected, the relationship between sensitivity and hematoma location was established for analysis. The results show that the azimuth and horizontal position of the hematoma can be accurately detected by the array scanning sensitivity method, and the detection effect is the best when the hematoma is located between the source and the detection distance. The depth only affects the overall luminous flux, and the deeper the position, the smaller the sensitivity. It is concluded that the array scanning sensitivity method can be used to quickly and accurately locate hematoma in a certain depths of brain tissue, which provides a new way of thinking and an effective reference for detecting tumors and optical imaging in tissue by near-infrared spectroscopy.

Keyword: Array scanning sensitivity; Functional near-infrared spectroscopy; Brain hematoma detection; Finite element method
引言

脑血肿多发生于颅脑损伤(traumatic brain injury, TBI)之后, 是损伤后常见且最为严重的继发性病变之一, 具有发病率高、 死亡率高等特点, 目前临床的检测手段主要是磁共振成像(magnetic resonance imaging, MRI)和计算机断层扫描(computed tomography, CT)等影像学方法, 虽然检测结果准确率高, 但是设备体积大、 成本高, 不适合连续的动态检测, 且影像学方法具有放射性[1]。 而功能性近红外光谱技术(functional near-infrared spectroscopy, fNIRS)具有无创、 实时、 可连续检测等优点, 且近红外光在“ 光学窗” 波段内(650~950 nm), 对皮下几厘米的生物组织具有良好的穿透性, 通过测定脑组织的入射光强度和出射光强度, 分析光的衰减信息可实现脑部疾病的快速检测, 因此功能性近红外光谱技术已被广泛应用于食品、 农业、 药物、 临床医学等各大领域, 成为众多学者的研究重点[2]。 自美国宾夕法尼亚大学的Chance[3]等利用光在组织内的传输特性判断脑血肿的发生取得较好效果后, Salonia[4]等利用近红外光对儿童颅脑出血进行研究, Sultan[5]等利用三维有限元法对光子在人类头部的传播行为进行数值模拟并取得可观效果; 国内王金海[6]等利用多通道差分吸光度法研究了组织内异物的快速检测。 为了能够进行头部的全方位探测, 在前人的研究基础上基于近红外光谱技术提出一种阵列扫描式灵敏度法, 结合单源多探测器建立脑组织的有限元模型, 光源发射光子进入脑组织, 在组织中进行吸收、 散射后, 可在全方位的阵列探测器处获取出射光信息, 处理信息得到灵敏度矩阵, 建立灵敏度与血肿位置的关系图。 分析得出结论: 通过开放式全方位的阵列灵敏度扫描获得灵敏度曲线图, 可以预测一定深度下的颅内血肿的位置信息, 为近红外无损诊断提供了新思路。

1 模型建立与仿真
1.1 扩散方程与灵敏度

辐射传输方程(radiative transfer equation, RTE)为光在组织中的传播提供了精确描述, 由于计算复杂, 变量较多, 一般情况下使用其近似解分析光在组织中的传播[7]。 扩散方程(diffusion equation, DE)是RTE的一阶球谐展开近似, 如式(1)

1c∂Φ(r, t)∂t-∇D(r)∇Φ(r, t)+μa(r)Φ(r, t)=S(r, t)(1)

式(1)中, Φ (r, t)是光通量, c是介质中的光速, t是时间, r是光源到探测器的距离, μa是吸收系数, S(r, t)是光源, D是扩散系数, 其表达式如式(2)

D(r)=13(μa+μ's)(2)

式(2)中, μ's是约化散射系数, 数值为(1-g)μs, g是平均散射余弦。

对于测得的光通量, 计算光的吸收信息

ΔI=I0-I(3)

式(3)中, I0为入射光强度, I为出射光强度。 本研究定义灵敏度为出射光强度相对入射光强度的变化率, 即相对吸收率

ΔS=I0-II0(4)

1.2 有限元建模

采用有限元(finite element method, FEM)仿真软件对光子在正常脑组织和含血肿脑组织中的传输进行模拟仿真, 通过求解偏微分方程或偏微分方程组来实现各种物理过程的仿真。 本工作是研究光源在稳定条件下的传播, 不考虑时间, 因此采用Helmholtz方程对光在组织中的传播进行有限元数值分析[8], 如式(5)

∇(-c∇u)+au=f(5)

式(5)中, u为光通量。 与式(1)对比, a是吸收系数, c是扩散系数, f是光源。 模型的边界条件采用Dirichlet和Neumann边界条件, 用来设置边界处的期望通量率u[9], 如式(6)和式(7)

u=r(6)

-n⃗(-c∇u)=g-qu(7)

其中, n⃗是边界上向外的单位法向量, g是边界上的源项, 稳态下为0, q是与内反射相关的正数, 用于空气与介质及介质界面的匹配边界下, q=0。

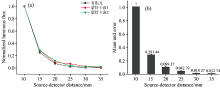
为验证有限元仿真的准确性, 建立一单层有界模型, 根据式(6)和式(7)设置边界条件, 将仿真结果与汪立宏[10]的蒙特卡洛(Monte Carlo, MC)模拟结果对比。 其模型光学参数为: 组织厚度h=2 cm, 相对折射率n=1, 吸收系数μa=0.19 cm-1, 约化散射系数μ's=6.4 cm-1, 平均散射余弦g=0.75, 仿真光子数为3× 105。 在不同探测位置得到光通量信息, 取有限元仿真结果与蒙特卡洛的两次仿真结果进行归一化, 并做平均处理与误差分析, 如图1所示。

图1 有限元与蒙特卡洛的仿真数据与平均比例
(a): 有限元与蒙特卡洛的仿真对比; (b): 仿真结果的平均比例与误差Fig.1 The simulation data and average ratio of finite element and Monte Carlo methods
(a): Simulation comparison between finite element and Monte Carlo methods; (b): The average detection ratio and error of the simulation results

由图1可知, 有限元与蒙特卡洛的仿真结果误差很小, 近乎吻合, 对数据做平均与误差处理如图1(b)所示, 得到平均探测比例, 误差棒表明误差范围。 该对比实验证明有限元仿真的数据可靠, 可研究光子在脑组织中的传播。

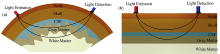
根据脑部结构, 脑组织模型可分为五层: 头皮(scalp)、 颅骨(skull)、 脑脊液(cerebrospinal fluid, CSF)、 灰质(gray matter)和白质(white matter), 如图2(a)所示, 部分结构的几何形状较为复杂, 可以认为组织之间是平行的, 以几何模型来代替头颅模型, 其大小为100 mm× 100 mm× 50 mm, 如图2(b)所示。

图2 脑组织模型
(a): 正常模型; (b): 简化模型Fig.2 Models of brain tissue
(a): Normal model; (b): Simplified model

根据相关文献[6]得知, 由于颅脑外伤造成的脑部血肿多为硬膜位置血肿, 即颅脑遭受创伤后, 血红蛋白细胞聚集于脑脊液层, 形成血肿, 因此设置血肿位于脑脊液层, 且血肿产生时对近红外光的吸收系数较周围组织强10倍以上。 表1是颅脑组织在波长为850 nm时的光学参数。

表1 颅脑组织在波长为850 nm的光学参数[11] Table 1 Optical parameters of the head model at 850 nm

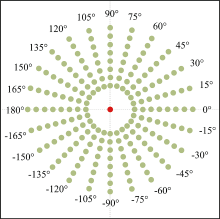
单源多检测器是由单个光源, 全方位阵列探测器包围组成, 其设置如图3所示, 中间红色部分为光源, 周围的浅色部分为探测器, 以横向正方向为0° , 逆时针为正, 顺时针为负, 每一相邻阵列的探测器间隔为15° , 光源与探测器半径均为1 mm, 设置源-探测器距离d为10~45 mm, 以5 mm为间隔。

图3 单源多检测器阵列Fig.3 Single-source multi-detectors array

设置光源发射光通量u为105, 即I0=105, 为减少误差提高精确度, 构建网格时设置全部域为极细化。 为探讨血肿对光通量、 探测灵敏度的影响, 在正常组织模型中插入血肿进行仿真计算。

2 结果与讨论

设置光源坐标为(0, 0, 50), 在组织中插入一个球状血肿, 坐标为(10, 0, 39) , 半径为4 mm, 对正常脑组织模型与含血肿的脑组织模型进行仿真, 其光子在组织中传播的仿真效果图及组织不同层的光通量分布如图4所示。

图4 光子在脑组织中传播的仿真
(a): 仿真图(正常脑组织); (b): 不同组织层的光通量分布(正常脑组织); (c): 仿真图(含血肿脑组织); (d): 不同组织层的光通量分布(含血肿脑组织)Fig.4 Simulated photons travel through brain tissue
(a): Diagram of simulation (normal brain tissue); (b): Distribution of light flux in different layers of brain tissue (normal brain tissue); (c): Diagram of simulation (brain tissue containing hematoma); (d): Distribution of light flux in different layers of brain tissue (brain tissue containing hematoma)

图4(a)和(c)是光子穿过组织的仿真图, 与图4(a)对比, 图4(c)有一圆环形状, 结合图例发现该位置的光通量比周围组织大约低7个单位。 图4(b)和(d)是光子传播时不同组织层的光通量分布图, 横坐标表示组织模型的横向总长度, 纵坐标是光通量u取自然对数, 其中第一层(即头皮表层)的峰值处A是光源, 纵坐标约为11.51, 宽度为2 mm, 其他层的峰值均位于光源正下方。 与图4(b)对比, 图4(d)在弧长为60 mm附近, 即插入的血肿位置处, 光通量有明显变化。

综上, 有限元仿真软件在图像与数据方面反映了血肿对光的传播有极大影响。 因此, 我们猜测: 利用探测光强度的灵敏度, 采取单边扫描的方法可以进行血肿定位。 为了确定这一判断, 改变血肿的方位、 横向位置与纵向深度验证猜测是否正确。

2.1 血肿的方位与灵敏度的关系仿真与结果

血肿在横向、 纵向位置相同的情况下, 改变其方位。 设置血肿横向、 纵向距离分别为10和11 mm, 方位设为0° , 30° 和60° , 仿真计算每个阵列的探测灵敏度如图5所示。

图5 血肿位置与部分方位阵列的探测灵敏度曲线图
(a): 血肿位于0° 阵列; (b): 血肿位于0° 时的部分探测灵敏度曲线图; (c): 血肿位于30° 阵列; (d): 血肿位于30° 时的部分探测灵敏度曲线图; (e): 血肿位于60° 阵列; (f): 血肿位于60° 时的部分探测灵敏度曲线图; 图注: d表示源-探测器距离Fig.5 The location of the hematoma and detection sensitivity curves of partial azimuth arrays
(a): Hematoma located at 0° ; (b): Sensitivity curves of the hematoma at 0° ; (c): Hematoma located at 30° ; (d): Sensitivity curves of the hematoma at 30° ; (e): Hematoma located at 60° ; (f): Sensitivity curves of the hematoma at 60°
Note: d is the source-detector distance

图5(a), (c)和(e)分别表示血肿位于0° , 30° 和60° 方位, 图5(b), (d)和(f)分别是对应血肿位置下部分方位阵列的灵敏度曲线图, 这里选取的方位阵列在图5(a), (c)和(e)中标记为橙色。 当血肿位于0° 方位时, 如图5(a), 扫描各方位角的灵敏度得到图5(b), 发现0° 方位阵列的灵敏度最大, 随着与0° 方位阵列的距离增加, 灵敏度逐渐减小, 处于血肿对称位置的180° 方位阵列的灵敏度最小, 接近0。 当血肿位于30° 和60° 方位时, 如图5(c)和(e), 分析对应的灵敏度线图, 发现血肿所在的方位灵敏度最大, 距离血肿方位越远, 灵敏度越小; 其中还可以得到源-探测器距离越大, 灵敏度越大, 这一结果符合文献[12]表述。 因此可以确定: 采用灵敏度的阵列式扫描, 可以准确预测血肿的方位。

2.2 血肿的横向位置与灵敏度的关系仿真与结果

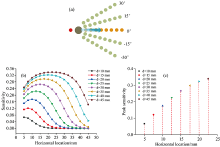
血肿在同一深度的情况下, 改变其横向位置。 设置血肿位于0° 方位, 其纵向位置距离表层11 mm, 横向坐标为5~45 mm, 以2.5 mm为间隔, 仿真结果如图6所示。

图6 血肿在不同水平位置下的灵敏度曲线图
(a): 血肿的水平位置; (b): 不同水平位置下的灵敏度曲线图; (c): 不同探测点的峰值灵敏度图Fig.6 Sensitivity curves of hematoma at different horizontal locations
(a): Horizontal position of the hematoma; (b): Sensitivity curves at different horizontal positions; (c): Peak sensitivities at different detection points

由图6(b)可看出当血肿水平移动时, 每个探测点的灵敏度发生不同趋势的改变, 随着血肿的横向位置增加, d=10 mm处的探测灵敏度逐渐减小, d=15, 20, 25, 30, 35, 40和45 mm处的探测灵敏度增加到一定峰值后又逐渐减小。 从线图中提取出每个探测点的灵敏度峰值, 如图6(c)所示, 发现各探测点的灵敏度峰值出现时, 血肿的水平位置是该探测距离的1/2。 即在某一方位上, 当血肿位于源与某一探测器距离中间时, 该探测点的灵敏度最大, 探测效果最好。 因此可以确定: 采用灵敏度的阵列式扫描, 可以探测光的横向位置信息。

2.3 血肿的纵向深度与灵敏度的关系仿真与结果

血肿在同一位置的情况下, 改变其纵向深度。 血肿在脑组织中会渗透到上下层组织, 设置血肿与表层的距离为7, 9, 11和13 mm, 仿真结果如图7所示。

图7 血肿在不同深度下的灵敏度曲线图
(a): 血肿的纵向深度; (b): 灵敏度曲线图
图注: 图中白色部分表示血肿Fig.7 Sensitivity curves of hematomas at different depths
(a): The depth of the hematoma; (b): Sensitivity curves
Note: The white area in Fig.7(a) indicates a hematoma

由图7可以得到: 随着血肿的纵向深度的增加, 探测灵敏度逐渐减小, 且不同深度的灵敏度改变趋势整体相同。 即血肿的纵向位置越深, 光子经过的概率越小, 但是深度并不影响整体趋势, 因此采用灵敏度的阵列式扫描, 可以定位到一定深度下的血肿。

3 结论

利用有限元仿真软件模拟了光在正常脑组织和含血肿脑组织中的传输, 通过改变血肿的方位、 横向位置与纵向深度, 采用阵列扫描式灵敏度法获取全方位的灵敏度矩阵, 分析位置信息与灵敏度的关系图, 结果显示该方法可以准确探测血肿的方位与横向信息, 且血肿位于源与探测距离中间时, 探测效果最佳, 而纵向深度只影响整体光通量, 随着深度增加, 探测灵敏度逐渐减小, 因此可探测一定深度下的血肿信息。 确定了阵列扫描式灵敏度法能够帮助近红外光谱技术实现开放式全方位的血肿探测, 为该领域的无创检测与应用起到了一定的参考意义与推进作用。

参考文献
[1] Wang J, Lin J, Chen Y, et al. Journal of Biomedical Optics, 2019, 24(4): 1. [本文引用:1]
[2] Paola Pinti, Ilias Tachtsidis, Antonia Hamilton, et al. Annals of the New York Academy of Sciences, 2020, 1464(1): 5. [本文引用:1]
[3] Robertson C S, Gopinath S P, Chance B. Journal of Biomedical Optics, 1997, 2(1): 31. [本文引用:1]
[4] Salonia R, Bell M J, Kochanek P M, et al. Journal of Neurotrauma, 2012, 29(3): 1047. [本文引用:1]
[5] Sultan E, Pourrezaei K, Ghand jbakhche A, et al. International Journal for Numerical Methods in Biomedical Engineering, 2014, 30(3): 353. [本文引用:1]
[6] WANG Jin-hai, LIU Dong-yuan, WANG Hui-quan, et al(王金海, 刘东远, 王慧泉, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2018, 38(10): 3205. [本文引用:2]
[7] XU Ke-xin, GAO Feng, ZHAO Hui-juan(徐可欣, 高峰, 赵会娟). Biomedical Photonics(生物医学光子学). Beijing: Science Press(北京: 科学出版社), 2011. 49. [本文引用:1]
[8] Sultan E, Najafizadeh L, Gand jbakhche A H, et al. Journal of Biomedical Optics, 2013, 18(1): 17008. [本文引用:1]
[9] Sultan E, Gand jbakhche A H, Pourrezaei K, et al. BioMedical Engineering OnLine, 2018, 17(1): 176. [本文引用:1]
[10] Wang L, Jacques S L, Zheng L. Computer Methods and Programs in Biomedicine, 1995, 47(2): 131. [本文引用:1]
[11] Eggebrecht A T, White B R, Ferradal S L, et al. NeuroImage, 2012, 61(4): 1120. [本文引用:1]
[12] Feng W, Haishu D, Fenghua T, et al. Physiological Measurement, 2001, 22(1): 201. [本文引用:1]