表面粗糙样品的太赫兹光谱参数提取方法研究

引用本文

于洋, 张朝晖, 赵小燕, 张天尧. 表面粗糙样品的太赫兹光谱参数提取方法研究[J]. 光谱学与光谱分析, 2022,42(2): 386-391.
YU Yang, ZHANG Zhao-hui, ZHAO Xiao-yan, ZHANG Tian-yao. Study on Extraction Method of Terahertz Spectral Parameters of Rough Surface Samples[J]. Spectroscopy and Spectral Analysis, 2022,42(2): 386-391.
Doi:10.3964/j.issn.1000-0593(2022)02-0386-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

表面粗糙样品的太赫兹光谱参数提取方法研究

于洋¹, 张朝晖^1,^2,^*, 赵小燕¹, 张天尧¹

1.北京科技大学自动化学院仪器科学与技术系, 北京 100083

2.北京市工业波谱成像工程技术研究中心, 北京 100083

*通讯作者 e-mail: zhangzhaohui@ustb.edu.cn

作者简介: 于洋, 1992年生, 北京科技大学自动化学院控制科学与工程专业博士研究生 e-mail: ustbyuyang@sina.cn

收稿日期: 2021-02-01 修回日期: 2021-05-05 接受日期: 2021-05-05

基金: 国家自然科学基金项目(62005014)和中央高校基本科研业务费专项资金项目(FRF-TP-20-015A1)资助

摘要

很多物质在太赫兹波段内的光谱参数具有指纹特征, 这是太赫兹技术在安检等众多领域有所应用的基础。但是, 目前常用的太赫兹时域光谱(THz-TDS)技术提取物质光学参数的Duvillaret算法, 要求样品上下表面平行且充分光滑。然而在很多有潜力的实际应用场合中, 尤其是对于固体样品, 表面粗糙度不可避免, 并且不能使用模具压片等实验室制样手段来保证其表面的平行光滑特性, 由此需要一种不受样品表面粗糙度影响且更具有普适性的光学参数提取算法来增加太赫兹时域光谱技术在实际场合下的应用能力。分析了太赫兹波透射表面粗糙样品的光程, 建立了包含有样品粗糙度、折射率和消光系数的表面粗糙样品太赫兹透射模型, 在已知粗糙度及平均厚度的条件下, 提取出在太赫兹波段有特征吸收的表面粗糙样品的折射率和吸收系数, 验证了此透射模型的适用性。首先, 选择在太赫兹波段有特征吸收的α-乳糖和L-组氨酸作为实验材料, 制作了质量分数和密度相同的表面粗糙样品和光滑样品, 并在太赫兹时域光谱系统中获取它们的太赫兹透射实验数据; 然后, 利用建立的透射模型从实验数据中提取出了表面粗糙α-乳糖和L-组氨酸样品的折射率和吸收系数; 最后, 为衡量透射模型提取结果的优劣性, 把Duvillaret算法作为另一种光学参数提取的参照方法, 将本模型算法、 Duvillaret算法对表面粗糙样品的提取结果分别与从平行光滑样品中提取的标准结果进行比较, 计算两种提取方式与标准值之间的均方根误差(RMSE)。比较结果表明, 相比于Duvillaret算法, 本透射模型方法所提取出的表面粗糙样品的折射率和吸收系数与标准值之间偏差更小, 在一定程度上减少了粗糙度对提取结果的影响, 具有更高的精确度。因此, 在已知表面粗糙样品的粗糙度以及平均厚度的条件下, 利用此模型可较为精确地在太赫兹时域光谱系统中提取出物质的光学参数。此研究结果将有力推进太赫兹波光学参数提取技术的实际应用。

关键词: 太赫兹时域波谱技术; 透射模型; 粗糙度; 光学参数

中图分类号:O657.61 文献标志码:A

Study on Extraction Method of Terahertz Spectral Parameters of Rough Surface Samples

YU Yang¹, ZHANG Zhao-hui^1,^2,^*, ZHAO Xiao-yan¹, ZHANG Tian-yao¹

1. School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China

2. Beijing Engineering Research Center of Industrial Spectrum Imaging, Beijing 100083, China

Abstract

The spectral parameters of many substances within the terahertz band have fingerprint characteristics, which is the basis of the application of the terahertz technology in many fields such as security inspection. However, it is required that the upper and lower surfaces of samples should be parallel and smooth for the Duvillaret algorithm, which is commonly used to extract the optical parameters of materials in terahertz time-domain spectroscopy (THz-TDS). Moreover, surface roughness is inevitable, and laboratory sample preparation methods such as mold pressing can not be utilized to ensure the parallelism and smoothness of the surface in many potential practical applications, especially for solid samples. Therefore, a universal optical parameter extraction algorithm that is not easily affected by the surface roughness of samples is needed to increase the application ability of THz-TDS in different situations. In this paper, the optical path of the transmission of the terahertz wave through rough samples is analyzed, and a terahertz transmission model of rough samples, including roughness, refractive index and extinction coefficient parameters, is established. Under the condition of known roughness and average thickness, the applicability of the transmission model is verified by extracting the refractive index and absorption coefficient of rough samples with characteristic absorption peaks in the terahertz band. -----The α-Lactose and L-Histidine which have typical absorption features at terahertz frequencies are selected as experimental material. Pellets at the same concentration are prepared and further separated into the rough surface group and smooth surface group. The refractive index, as well as absorption coefficient, are calculated with both our proposed model and conventional Duvillaret algorithm. The comparison between the results is further analyzed for evaluating our method, the root-mean-square error (RMSE) between the two extraction methods and the standard value is calculated, and the extraction results of the transmission model, the Duvillaret algorithm and the standard value extracted from the parallel and smooth sample are compared at the same time. The comparison results show that, compared with the Duvilaret algorithm, the refractive index and absorption coefficient of the rough sample extracted by the transmission model method has smaller deviations from the standard value, which reduces the influence of roughness on the extraction result to a certain extent and has higher accuracy. Therefore, under the condition of known roughness and average thickness of the surface rough sample, this model can be used to more accurately extract the optical parameters of the substance in the terahertz time-domain spectroscopy system. The research results will greatly promote the practical application of terahertz optical parameter extraction technology.

Keyword: Terahertz time-domain spectroscopy; Transmission model; Roughness; Optical parameters

文章图片

引言

由于太赫兹时域光谱的探测具有相干特性^{[1, 2, 3]}, 能同时记录样品的幅值和相位信息, 因此已经广泛用于物质光学参数的定量计算中^{[4, 5, 6, 7]}。然而在测试固体样品之前, 需要通过研磨及压片等手段来获得表面平行且光滑的样品^{[8, 9]}, 只有透射过平行且光滑样品的太赫兹波才能使用常用的Duvillaret算法来对物质的光学参数进行定量计算^[10]。但是在很多实际应用场合如考古研究, 机场安检等, 样品表面形态各异, 且不可对检测对象表面进行处理, 因此需要一种更贴近实际并能适应样品表面粗糙的光学参数提取模型, 来增加太赫兹时域光谱技术在实际场合下的应用能力。

在我们的前期工作^[11]中, 主要研究了单粗糙面样品的太赫兹透射问题, 建立了包含有样品表面粗糙度、消光系数和折射率参数的太赫兹透射模型, 选择在太赫兹波段没有特征吸收的聚四氟乙烯样品来验证了模型的适用性。但是, 它并不适用于双粗糙面样品的太赫兹透射过程及光学参数的提取。本文改进了文献[11]的方法, 建立了更贴合实际应用的双表面粗糙样品的太赫兹透射模型, 可在已知的上下表面粗糙度及平均厚度的条件下提取出反映物质特征的光学参数。

1 Duvillaret光学参数提取算法

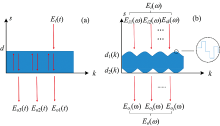
在太赫兹时域波谱系统中, 理想样品指的是表面光滑且平行的样品, 理想样品光学参数提取算法是由Duvillaret等^[10]在1996年提出的。如图1(a)所示, 时域太赫兹波E_i(t)垂直入射到厚度为d, 复折射率为 $\tilde{n}$ (ω )的光滑样品表面, 复折射率 $\tilde{n}$ (ω )=n(ω )-iκ (ω ), n(ω )与κ (ω )分别为折射率与消光系数。入射太赫兹波在样品内部发生多次反射。将回波截断只留取主波之后, 对时域信号和参考信号进行傅里叶变换分别得到E_s(ω )与E_r(ω ), 则折射率n(ω )与消光系数κ (ω )分别为

$n (ω) = 1 - \frac{c}{ωd} ∠ H (ω)$ (1)

$κ (ω) = - \frac{c}{ωd} \ln \{| H (ω) | \frac{[1 + n {(ω)]}^{2}}{4 n (ω)}\}$ (2)

其中, ω 和c分别为角频率和真空中的光速, 光滑样品的厚度为d, H(ω )为传递函数, 由E_s(ω )与E_r(ω )相除得到。

	Figure Option View Download New Window
	图1 表面平行光滑样品的太赫兹透射示意图(a)表面粗糙样品的太赫兹透射示意图(b)Fig.1 Transmissive schematic diagram of THz through a sample with parallel and smooth surfaces (a); Transmissive schematic diagram of THz through a sample with rough surfaces (b)

在测量固体样品时, 为使用此算法进行样品折射率和吸收系数的提取, 通常需要使用研钵和压片机等工具制得表面平行且光滑的样品后才能进行太赫兹波谱测试, 这使得利用太赫兹波谱技术对样品进行折射率和吸收系数的定量分析时需要平行且表面光滑的样品为前提, 这大大减弱了太赫兹波谱技术在实际场合中的应用能力, 然而Duvillaret光学参数提取算法对于粗糙样品的适用性需要进一步讨论与分析。在此次研究中, 将粗糙样品的平均厚度作为参数d代入式(1)和式(2)中提取出表面粗糙样品的折射率和吸收系数, 并将此方式提取的结果与透射模型的提取结果进行优劣性比较。

2 透射模型光学参数提取算法

由图1(a)可见, 对于入射太赫兹波来说, 每一个入射点所对应的样品厚度都相同, 因此各入射点太赫兹波在样品内部的传输光程相同。对于平行且光滑样品而言, 此算法有着较高的精确度。但是当入射表面粗糙时, 不同太赫兹入射点所对应的样品厚度各不相同, 太赫兹在样品内部的传播光程也会各不相同。此时在提取样品的吸收系数及折射率时需要考虑样品表面粗糙度参数, 以下为表面粗糙样品透射模型的建立过程。

假设待测样品满足如下条件^[11]: (1)粗糙表面高度分布符合高斯型分布; (2)样品均匀且各向同性, 太赫兹光斑尺寸远大于样品表面相关长度; (3)样品表面粗糙度稍小于入射波波长。

建模过程如上图1(b)所示, 将入射太赫兹波E_i(ω )平均分为N个入射波微元, 每个入射波 $E_{i_{k}}$ (ω )入射点对应不同的粗糙表面高度d(k)和透射波 $E_{o_{k}}$ (ω ), 则探测器接收到的透射波E_o(ω )可表示为所有透射波之和。将粗糙样品的上下表面分割为宽度相同、高度不同的平行微元表面, 则每个入射太赫兹微元垂直入射到上表面后, 沿垂直下表面方向透射出样品表面, 则透射太赫兹波可以表示为

$E_{o} (ω) = \overset{N}{\sum_{k = 1}} \frac{E_{i} (ω)}{N} \frac{4 n (ω)}{(1 + n {(ω))}^{2}} \exp (- \frac{i \tilde{n} (ω) ωd (k)}{c})$ (3)

式(3)中, ω 和c分别为角频率和真空中的光速, 复折射率 $\tilde{n}$ (ω )=n(ω )-iκ (ω ), n(ω )与κ (ω )分别为折射率与消光系数, d(k)为 $E_{i_{k}}$ (ω )对应的入射点表面厚度。粗糙样品上表面不同点高度为d₁(k), d₁(k)是均值为μ₁(μ₁> 0), 方差为 $δ_{1}^{2}$ 的高斯分布。粗糙样品下表面不同点的高度为d₂(k), d₂(k)是均值为μ₂ (μ₂> 0), 方差为 $δ_{2}^{2}$ 的高斯分布。 d₁(k)与d₂(k)的分布相互独立, 则由统计学规律可知d(k)=d₁(k)-d₂(k)是均值为μ=μ₁-μ₂, 方差为δ ²= $δ_{1}^{2}$ + $δ_{2}^{2}$ 的高斯分布。将式(3)表示成集合平均形式后可得到

$E_{o} (ω) = E_{i} (ω) \frac{4 n (ω)}{(1 + n {(ω))}^{2}} < \exp (- \frac{i \tilde{n} (ω) ωd (k)}{c}) >$ (4)

如果样品表面高度分布d(k)符合高斯分布, 那么式(4)中的集合平均项可以写成如式(5)形式^[11]

$\begin{array}{l} < \exp (- \frac{i \tilde{n} (ω) ωd (k)}{c}) > = \exp (- \frac{i \tilde{n} (ω) ωμ}{c}) \cdot \\ \exp (- \frac{{\tilde{n}}^{2} (ω) ρ^{2} ω^{2} δ^{2}}{2 c^{2}}) \end{array}$ (5)

将样品信号E_o(ω )与参考信号E_r(ω )=E_i(ω )exp(-iω μ/c)相除后, 得到表面粗糙样品的传递函数H(ω )

$\begin{array}{l} H (ω) = \frac{4 n (ω)}{(1 + n {(ω))}^{2}} \cdot \\ \exp [\frac{(κ^{2} (ω) - n^{2} (ω)) ρ^{2} ω^{2} δ^{2} - 2 cκ (ω) ωμ}{2 c^{2}}] \cdot \\ \exp [i \frac{n (ω) κ (ω) ρ^{2} ω^{2} δ^{2} + (1 - n (ω)) cωμ}{c^{2}}] \end{array}$ (6)

式(6)中, ρ 为等于0.2的参数^[11], 则传递函数H(ω )的幅值A(ω )和相位φ (ω )分别为

$\begin{array}{l} A (ω) = \frac{4 n (ω)}{(1 + n {(ω))}^{2}} \cdot \\ \exp [\frac{(κ^{2} (ω) - n^{2} (ω)) ρ^{2} ω^{2} δ^{2} - 2 cκ (ω) ωμ}{2 c^{2}}] \end{array}$ (7)

$φ (ω) = \frac{n (ω) κ (ω) ρ^{2} ω^{2} δ^{2} + (1 - n (ω)) cωμ}{c^{2}}$ (8)

3 实验部分

3.1 样品制备及数据采集

实验选择McLean公司生产的纯度99.5%的α -乳糖一水合物和沪试公司生产的纯度99.0%的L-组氨酸作为实验材料, 稀释剂为由Micro-Powders公司生产的粒度在13~21 μm之间的聚四氟乙烯(PTFE)。由于在样品上下两表面两次剥离砂纸的过程中容易造成样品碎裂及表面粗糙度测量问题等限制原因, 所以在实验部分以制得的单表面粗糙样品为实验样品, 即样品上表面粗糙, 下表面光滑。以制作单粗糙面α -乳糖样品为例。首先, 将2.34 g的PTFE和0.12 g乳糖放入研钵中进行充分的混合研磨。然后, 将砂纸放入磨具后倒入混合物粉末进行压片, 所有样片的压片时间和压强统一为3 min和6 MPa。从磨具中取出样片后, 用镊子将砂纸从样片中剥离, 即可得到一面粗糙一面光滑的样品。同时按照传统标准方式制得与单粗糙面样品质量分数相同, 质量为0.44 g, 厚度为1.58 mm的双表面光滑样品。由于压片的时间和压强相同, 因此样片的密度可认为近似相同, 平均每克乳糖样品的厚度为1.58 mm/0.44=3.59 mm, 由此根据粗糙乳糖样品的质量可得到粗糙样品的平均厚度。重复上述步骤制得粗糙L-组氨酸样品。样品的粗糙度由型号为OLS4100的奥林巴斯激光共聚焦显微镜扫描获得。样品的具体信息参见表1。

表1 α -乳糖及L-组氨酸样品信息 Table 1 Information on the α -Lactose and L-Histidine sample

本文中所使用的太赫兹透射式时域谱仪具体工作原理和光路图详情请参考文献[12]。所有样品的太赫兹透射时域数据采集流程是相同的。首先进行空载情况下参考信号的测量, 之后为了降低随机误差的影响, 连续采集三次信号后求取其平均值作为样品的时域透射信号。充入干燥氮气后当湿度降低到5%开始进行实验, 所有采集过程都是在密闭环境中进行。

3.2 数据处理

完成信号采集后, 首先对时域中的参考信号和样品信号进行傅里叶变换后分别得到频域信号。然后, 提取出频域信号的幅值信息。其中针对相位信息中的解扰卷误差传递问题, 参照文献[13]的方法对相位进行处理, 处理后得到相位信息。由于样片表面上表面粗糙, 下表面光滑, 则利用激光共聚焦显微镜测得的上表面粗糙度即为参数δ 。利用幅值和相位信息分别按照透射模型[式(7)和式(8)]和Duvillaret算法[式(1)和式(2)]分别提取出吸收系数和折射率, 再计算它们与标准值之间的均方根误差。吸收系数α (ω )由消光系数κ (ω )按照α (ω )=2κ (ω )ω /c计算得到。

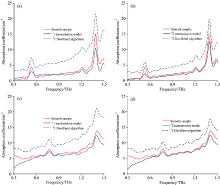
在利用透射模型公式进行表面粗糙样品的折射率和消光系数提取时, 令实验数据的幅值和相位分别与式(7)和式(8)相等, 在MATLAB软件中解方程即可获得表面粗糙样品的折射率和消光系数。最后计算两种方法提取结果与标准值之间的均方根误差, 由于质量分数和密度相同, 从双表面光滑的α -乳糖和L-组氨酸样品中提取的吸收系数和折射率可当作标准值。均方根误差按 $S = {\{\overset{N}{\sum_{i = 1}} (y_{i} - x_{i})^{2} / N\}}^{1 / 2}$ 计算得到。其中, y_i为提取值, x_i为标准值, N为数据点个数。

4 结果与讨论

按照上述顺序进行数据处理过后, 按照两种方法提取出表面粗糙α -乳糖和L-组氨酸样品的吸收系数和折射率分别如图2和图3所示, 其中红色曲线为从光滑样品中得到的标准值。 α -乳糖和L-组氨酸的吸收峰位置分别与文献[14, 15]中一致。

	Figure Option View Download New Window
	图2 #1α -乳糖样品吸收系数曲线(a); #2α -乳糖样品吸收系数曲线(b); #1L-组氨酸样品吸收系数曲线(c); #2L-组氨酸样品吸收系数曲线(d)Fig.2 Absorption waveforms of the #1 α -Lactose sample (a) and the #2 α -Lactose sample (b); Absorption waveforms of the #1 L-Histidine sample (c) and the #2 L-Histidine sample (d)

	Figure Option View Download New Window
	图3 #1α -乳糖样品折射率曲线(a); #2α -乳糖样品折射率曲线(b); #1L-组氨酸样品折射率曲线(c); #2L-组氨酸样品折射率曲线(d)Fig.3 Refractive index waveforms of the #1 α -Lactose sample (a) and the #2 α -Lactose sample (b); Refractive index waveforms of the #1 L-Histidine sample (c) and the #2 L-Histidine sample (d)

4.1 吸收系数

两种不同方式提取出的单粗糙面样品的吸收系数曲线如图2所示。对于Duvillaret算法来说, 样品表面粗糙度越大, 探测器接受到的样品幅值越小。而幅值主要影响到样品吸收系数的提取。 Duvillaret算法中主要针对表面平行且光滑的样品, 没有考虑到样品表面粗糙度参数及由粗糙度造成的幅值衰减作用, 所以导致由粗糙度引起的幅值衰减被当成是样品的吸收, 使得吸收系数曲线明显高于标准值。 #1 α -乳糖和#1 L-组氨酸样品的粗糙度值分别为145.2和131.2 μm, 从图2可见, Duvillaret算法对于粗糙度在145.2 μm以下的α -乳糖和L-组氨酸能够实现定性识别, 但是不能实现精确度较高的定量计算。而物质在太赫兹频段吸收峰的强弱与该物质在某一频率分子的共振频率强弱等微观因素有关, 因此Duvillaret算法并不一定能对粗糙度在145.2 μm以下的所有物质进行特征识别。

根据表2中均方根误差数值可以判断出, 由Duvillaret算法提取出的表面粗糙样品的吸收系数与标准值之间的均方根误差要明显高于同种样品中由透射模型提取值的均方根误差, 且粗糙度对于Duvillaret算法的影响趋势为: 粗糙度越大, 均方根误差越大, 对定量计算的精确程度影响越大。利用Duvillaret算法提取出的α -乳糖和L-组氨酸的均方根误差分别从53.63升高到88.57, 从46.36升高到73.38。而对于同种粗糙程度的样品而言, 从表2中的均方根误差数据可以看出, 相比于Duvillaret算法, 透射模型的提取方法精确度更高, 可有效减少因为样品表面粗糙度而造成的幅值衰减问题, 例如#1和#2 α -乳糖样品的均方根误差分别从88.57降低到21.89, 从56.63降低到13.51。因此对于表面粗糙样品的吸收系数提取而言, 透射模型提取方法相比于Duvillaret算法有着更高的精确度。

表2 透射模型方法和Duvillaret算法提取出的吸收系数的均方根误差 Table 2 The root-mean-square error (RMSE) of absorption coefficient extracted by the transmission model and the Duvillaret algorithm

4.2 折射率

对于Duvillaret算法来说, 粗糙度参数对于吸收系数提取的影响较为明确, 提取值相对于标准值明显偏高。但从图3可以看出, 粗糙度对于Duvillaret算法的折射率的提取具有不确定性。提取值可能会高于标准值, 也可能会低于标准值。按照Duvillaret算法, 折射率的提取与平均厚度和相位差有关, 而相位差是一个与样品表面粗糙度无关的参数, 因此难以确定粗糙度对样品折射率提取结果的影响。

从表3中可以看出, 对于Duvillaret算法来说, 提取结果的均方根误差随着粗糙度增大而增大, 例如Duvillaret算法提取出的L-组氨酸的均方根误差从0.26升高到0.33。但对于相同样片的不同提取方法所获得的折射率数值来说, 透射模型的提取结果与标准值之间的均方根误差更小, 精确程度更高。例如对于L-组氨酸的#1样品, 透射模型提取结果的均方根误差为0.05, 远低于由Duvillaret算法所提取结果的均方根误差0.33。因此对于粗糙样品的折射率提取而言, 透射模型提取方法相比于Duvillaret算法有着更高的精确度。

表3 透射模型方法和Duvillaret算法提取出的折射率的均方根误差 Table 3 The root-mean-square error (RMSE) of refractive index extracted by the transmission model and the Duvillaret algorithm

5 结论

建立了表面粗糙样品的太赫兹透射模型, 选择在太赫兹波段有特征吸收的α -乳糖和L-组氨酸作为实验材料, 通过利用此透射模型提取出表面粗糙样品的吸收系数和折射率, 验证了此透射模型对于在太赫兹波段有特征吸收物质的适用性。为比较透射模型提取效果的优劣程度, 选择在太赫兹时域光谱领域中最常用的Duvillaret算法作为参照, 分别计算了两种不同方式提取结果与从双表面光滑样片中获得的标准值的均方根误差。相比于Duvillaret算法, 无论是吸收系数还是折射率的提取, 透射模型与标准值之间的偏差更小, 有着较高的精确度。在此篇研究中, 展示了一种适用于太赫兹时域光谱技术的表面粗糙样品光学参数的提取方法, 弥补了相关提取算法缺失的空白, 为全表面粗糙样品的光学参数提取提供了参考, 进一步增加了太赫兹时域光谱技术在实际应用领域的适用性。

参考文献

文献列表

[1]	Zhang T, Zhang Z, Arnold M A. Applied Spectroscopy, 2019, 73(3): 253. [本文引用:1]
[2]	Liebermeister L, Nellen S, Kohlhaas R, et al. Journal of Infrared, Millimeter, and Terahertz Waves, 2019, 40(3): 288. [本文引用:1]
[3]	Kong D Y, Wu X J, Wang B, et al. Optics Express, 2018, 26(14): 17964. [本文引用:1]
[4]	Peretti R, Mitryukovskiy S, Froberger K, et al. IEEE Transactions on Terahertz Science and Technology, 2019, 9(2): 136. [本文引用:1]
[5]	Mumtaz M, Mahmood M A, Shahzad A, et al. Journal of Infrared, Millimeter, and Terahertz Waves, 2020, 41(10): 1181. [本文引用:1]
[6]	Bernier M, Garet F, Kato E, et al. Journal of Infrared, Millimeter, and Terahertz Waves, 2018, 39(4): 349. [本文引用:1]
[7]	Zhang H, Zhang Z, Zhao X, et al. Chinese Optics Letters, 2018, 16(10): 103001. [本文引用:1]
[8]	ZHANG Tian-yao, ZHANG Zhao-hui, et al(张天尧, 张朝晖, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(6): 1689. [本文引用:1]
[9]	Yi W, Yu J, Xu Y, et al. Instrumentation Science & Technology, 2017, 45(4): 423. [本文引用:1]
[10]	Duvillaret L, Garet F, Coutaz J L. IEEE Journal of Selected Topics in Quantum Electronics, 1996, 2(3): 739. [本文引用:2]
[11]	Yu Y, Zhang Z, Zhang T, et al. Optical and Quantum Electronics, 2020, 52(5): 240. [本文引用:5]
[12]	Zhang T, Zhang Z, Zhao X, et al. Applied Optics, 2020, 59(16): 4775. [本文引用:1]
[13]	Withayachumnankul W, Naftaly M. Journal of Infrared, Millimeter, and Terahertz Waves, 2014, 35(8): 610. [本文引用:1]
[14]	Komand in G A, Gavdush A A, Goncharov Y G, et al. Optics and Spectroscopy, 2019, 126(5): 514. [本文引用:1]
[15]	Zong S, Ren G H, Li S, et al. Journal of Molecular Structure, 2018, 1157: 486. [本文引用:1]

2019

0.0