耦合多种特征的森林蓄积量反演方法比较——以雅鲁藏布江流域森林为例

引用本文

李子朝, 毕守东, 崔玉环, 郝泷. 耦合多种特征的森林蓄积量反演方法比较——以雅鲁藏布江流域森林为例[J]. 光谱学与光谱分析, 2022,42(10): 3263-3268.
LI Zi-zhao, BI Shou-dong, CUI Yu-huan, HAO Shuang. Comparison of Forest Stock Volume Inversion Methods Coupled With Multiple Features——A Case Study of Forest in Yarlung Zangbo River Basin[J]. Spectroscopy and Spectral Analysis, 2022,42(10): 3263-3268.
Doi:10.3964/j.issn.1000-0593(2022)10-3263-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

耦合多种特征的森林蓄积量反演方法比较——以雅鲁藏布江流域森林为例

李子朝, 毕守东, 崔玉环, 郝泷^*

安徽农业大学理学院, 安徽合肥 230036

*通讯作者 e-mail: haoshuang@ahau.edu.cn

作者简介: 李子朝, 1997年生, 安徽农业大学理学院硕士研究生 e-mail: 691039258@qq.com

收稿日期: 2021-06-29 修回日期: 2022-01-28 接受日期: 2022-01-28

基金: 国家自然科学基金项目(41801332)资助

摘要

森林资源遥感监测是遥感的重要应用方向之一。传统的统测方法花费大量的人力、物力, 科学的森林资源预测可以提升工作效率并降低测算成本。森林蓄积量是评价森林生态系统质量的重要指标。蓄积量反演模型是用来估测蓄积量的数学模型, 具有学习和预测的功能。同样的地物在不同光照或阴影区域有较大的差别, 利用波段比值可以在一定程度上减小光照和阴影区域在建模时得出结果的误差。森林蓄积量的预测模型通常选取光谱信息和纹理特征作为主要建模因子, 但未充分考虑选取波段比值、植被指数、地形因子等多特征变量时不同模型对预测精度的影响。针对不同模型的精度问题, 以西藏自治区米林县为研究区域, 以Landsat OLI影像、 DEM数据以及森林资源二类调查数据为数据源, 对光谱信息、纹理特征和地形因子等进行提取与分析, 并建立了三种基于多特征的森林蓄积量的反演模型, 分别是多元逐步回归模型、 BP神经网络模型和随机森林模型。旨在研究不同模型对森林蓄积量反演的影响。采用可决系数( R²)、平均绝对误差(MAE)和均方根误差(RMSE)来对模型进行拟合度和精度的评价。结果显示随机森林模型的拟合度和精度均为最优( R²=0.739, MAE=55.352 m³·ha^-1, RMSE=63.195 m³·ha^-1), 高于多元逐步回归模型( R²=0.541, MAE=58.317 m³·ha^-1, RMSE=71.562 m³·ha^-1)和BP神经网络模型( R²=0.477, MAE=67.503 m³·ha^-1, RMSE=73.226 m³·ha^-1)。模型预测值的范围为121.3~372.8 m³·ha^-1, 与实际值较为接近。结果表明基于多特征的森林蓄积量反演在实际应用中是有效的, 且不同的模型对森林蓄积量的反演精度有一定的影响。随机森林回归模型的反演精度最高, 能够较好地应用于森林资源的遥感监测中。该研究可以为森林蓄积量反演方法的选取提供参考和借鉴, 有助于森林资源遥感监测体系的不断完善。

关键词: 蓄积量反演; 多元逐步回归; BP神经网络; 随机森林; Landsat OLI

中图分类号:TP79 文献标志码:A

Comparison of Forest Stock Volume Inversion Methods Coupled With Multiple Features——A Case Study of Forest in Yarlung Zangbo River Basin

LI Zi-zhao, BI Shou-dong, CUI Yu-huan, HAO Shuang^*

School of Science, Anhui Agricultural University, Hefei 230036, China

*Corresponding author

Abstract

Remote sensing monitoring of forest resources is one of the important application directions of remote sensing. Traditional measurement methods cost a lot of workforce and material resources. Scientific forest resource prediction can improve work efficiency and reduce measurement costs. Forest stock volume is an important index to evaluate the quality of forest ecosystems. The forest stock volume inversion model is a mathematical model used to estimate the forest stock volume, which has the functions of learning and prediction. The same ground features are quite different in different light or shadow areas. The band ratio can be used to reduce the error of the results in modeling light and shadow areas to a certain extent. The forest stock volume prediction model usually selects spectral information and texture features as the main modeling factors. It does not fully consider the impact of different models on the prediction accuracy when selecting multi-characteristic variables such as band ratio, vegetation index, and topographic factors. In order to compare the accuracy of different models, this article takes Milin County in Tibet Autonomous Region as the research area, and uses Landsat OLI images, DEM data and forest resource survey data as data sources to extract analyze spectral information, texture features and topographic factors. Three forest volume inversion models based on multi-features are established. The three models are multiple stepwise regression models, BP neural network models and random forest models. The effects of different methods on the inversion of forest stock are studied. The coefficient of determination ( R²), mean absolute error (MAE), and root mean square error (RMSE) are used to evaluate the fit and accuracy of the model. The results showed that the fit and accuracy of the random forest model are the best ( R²=0.739, MAE=55.352 m³·ha^-1, RMSE=63.195 m³·ha^-1). The result is higher than the multiple stepwise regression model ( R²=0.541, MAE=58.317 m³·ha^-1, RMSE=71.562 m³·ha^-1) and BP neural network model ( R²=0.477, MAE=67.503 m³·ha^-1, RMSE=73.226 m³·ha^-1). The predicted value range of the model is 121.3~372.8 m³·ha^-1 and it is relatively close to the actual value. The results showed that the inversion of forest stock volume based on multi-features is effective in practical applications, and different models have different effects on the inversion accuracy of forest stock volume. The random forest regression model has the highest accuracy in this inversion study of forest stock volume, and it can be better applied to remote sensing monitoring of forest resources. This study can provide a reference for selecting forest stock volume inversion methods and help continuously improve the forest resource remote sensing monitoring system.

Keyword: Inversion of stock volume; Multiple Stepwise Regression; BP Neural Network; Random Forest; Landsat OLI

文章图片

引言

森林是地球之肺, 也是地球的基因库和能源库。在当今工业化时代, 大量二氧化碳和有害气体排放到空气中, 森林植被通过光合作用吸收二氧化碳并制造氧气的作用变得尤为重要, 净化空气的同时, 也起到了保护人类及其他动物生命健康的重要作用。随着交通运输业和工业的发展, 噪声污染对环境的影响越来越严重, 森林可以有效降低噪声的分贝, 改善人们的生活环境。森林还可以调节气候, 增加湿度的同时降低温度, 提高降水量。森林蓄积量是指一定区域里, 各种树木的木材总量, 是判断该区域森林茂盛程度的重要指标之一。

传统的森林资源的数据获取方法是实地勘察测量, 需要花费大量的人力、物力, 且调查结果误差较大。计算机、卫星和各种科学技术的发展, 使得遥感技术对森林蓄积量的反演研究成为国内外研究人员越来越熟悉的话题。例如郝泷等^[1]利用Landsat OLI影像估算了西藏林芝市的森林蓄积量, 菅永峰等^[2]以GF-2和SPOT-6数据为基础对湖北省太子山林场的森林蓄积量进行了研究, 曾伟生等^[3]利用机载激光雷达数据建立了东北林场的森林蓄积量估算模型, 朱思名等^[4]利用无人机影像对天山云杉林蓄积量进行了研究。遥感技术可以快速且准确地获取研究区域的森林光谱信息, 在大面积和人力难以到达区域的森林蓄积量的方向上有着明显的优势。例如郝泷等^[1]研究了地形因子和纹理特征对蓄积量反演的影响, 杨柳等^[5]估算了不同树种的蓄积量, 该方法的综合精度高于传统的实地测量, 且更适合于广泛应用。

常见的利用遥感技术对森林蓄积量进行反演的方法有很多。多元线性回归作为最经典的回归模型之一, 有着简单实用的优点, 但当自变量存在明显的线性相关时, 模型的精度可能不尽人意, 因此可以使用多元逐步回归分析, 按照自变量对因变量影响从大到小引入回归方程, 并剔除影响不显著的自变量, 从而建立最优回归方程。 BP神经网络有非线性映射能力和一定的自学习能力, 适用于内部机制复杂的问题。随机森林模型有着抗过拟合和擅长处理高维度数据的优点, 但运行速度较其他方法慢, 且需要根据不同的数据设置不同的参数^[6]。例如Ernest William Mauya等^[7]用多元线性回归估测了坦桑尼亚小规模人工林的蓄积量, 周俊宏等^[8]利用神经网络算法对普达措国家公园进行了遥感估算, 菅永峰等^[2]使用随机森林回归模型估测了湖北省太子山林场的森林蓄积量, 蒋馥根等^[9]利用KNN方法估测了旺业甸林场的森林蓄积量, 张超等利用偏最小二乘回归法估测了三峡水库区域的蓄积量。

本研究以西藏林芝市米林县为研究区域, 以Landsat OLI的多光谱数据、 DEM数据和森林资源二类调查数据为基础^[10], 采用多元线性逐步回归法、 BP神经网络和随机森林回归三种方法分别建立模型, 根据实际数据来设置相应的模型参数, 以达到每个模型的最优精度。将数据集分为训练集和测试集, 在模型建立后对其进行精度验证, 再将三种模型的精度进行比较, 分析并选择精度最高的模型。目的是通过不同模型对同一区域森林蓄积量的反演精度的比较, 为我国森林蓄积量反演研究模型选择提供参考。

1 实验部分

1.1 研究区概况

研究区域为西藏自治区林芝市米林县, 米林县位于西藏自治区的东南部, 地理坐标为: 北纬28° 39'— 29° 50', 东经93° 07'— 95° 12'。我国最长的高原河流雅鲁藏布江横穿全县, 米林县西高东低, 为山河谷地形。地球上最大、最深的峡谷— — 雅鲁藏布大峡谷坐落在米林县, 大峡谷景色壮阔, 地势险要, 堪称“ 人间秘境” 。米林县总面积为9 471 km², 平均海拔达到3 700 m, 森林覆盖率达48.11%, 年降水量600 mm以上, 拥有以雅鲁藏布江为主的天然水资源优势, 孕育了沿江两岸繁荣的森林生态系统, 物种多样性之丰富堪称生物基因库。

1.2 遥感影像数据获取及处理

选取Landsat OLI多光谱影像数据, 空间分辨率为30 m, 遥感影像的获取时间为2015年11月, 选取积雪覆盖面积较少的遥感影像, 可以更准确地获取地面植被的光谱信息, 有效减少模型预测结果的误差。对遥感影像进行预处理, 主要包括辐射定标、大气校正、正射校正等。

1.3 样地数据调查及处理

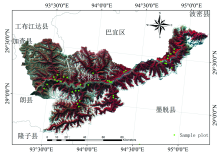
研究区共设样地35个, 地面实测数据采样完成时间为2015年9月— 11月, 样地调查的主要内容包括: 林种、优势树种、龄组、郁闭度、树高、胸径等林分信息, 及样地中心坐标、海拔、坡度、坡位等地形因子。研究区主要由针叶林、阔叶林、针阔混交林组成, 利用二元材积表^[11]对样地的蓄积量进行计算。由于研究区范围较大, 地形较复杂, 样地数据无法满足全区域的森林蓄积量估算, 因此在通过样地调查数据与森林二类资源调查数据准确性的验证后, 依据米林县的森林二类资源调查数据构建基于多特征的森林蓄积量反演模型。经过预处理后的研究区Landsat OLI假彩色影像和样地分布情况如图1所示。

	Figure Option View Download New Window
	图1 研究区范围及样地分布图Fig.1 Location and sample plots of the study area

异常值的存在会对分析结果平均值与标准差产生重要影响, 异常值的检验与正确处理是保证原始数据可靠性、平均值与标准差计算准确的前提。本研究使用Excel软件将样本点的数据全部导入, 首先将数据标准化, 再将极端离群值剔除(比如蓄积量为0的林地矢量点等), 再根据拉依达准则法(3δ )将小于μ -3σ 或者大于μ +3σ 的异常值按行删除, 保证样本数据总体接近正态分布。

1.4 多源数据处理及自变量筛选

单波段的信息比较单一, 为了能够提高模型的精度, 备选参数主要包括Landsat OLI遥感影像的7个单波段光谱数据、 5个植被指数、 11个波段比值、 DEM数据、森林资源二类调查数据和基于灰度共生矩阵(GLCM)的8种纹理特征。使用ArcGIS将以上数据提取至对应的样本点。将全部自变量引入构建的模型中不仅会使模型过于复杂, 而且也无法保证模型的精度, 通过皮尔森(Pearson)相关性分析, 筛选出与因变量蓄积量之间存在显著相关性的自变量因子, 利用这些变量因子构建模型可以有效提升模型构建的效率与精度。最终筛选出的变量包括郁闭度、 RVI、海拔、坡度、 Band5/Band4、 Band7/Band4、 Homogeneity_B1、 Entropy_B1、 SecondMoment_B1、 Correlation_B1。

1.5 基于多元逐步回归森林蓄积量反演

多元线性回归是最常见的分析多个自变量与一个因变量之间线性关系的回归方法。其优点是简单、实用。

假设样本数据中因变量为Y, 自变量为X₁, X₂, X₃, ..., X_n, 并且两者之间存在线性关系, 则多元线性回归模型的公式为

$Y = a_{0} + a_{1} X_{1} + a_{2} X_{2} + a_{3} X_{3} + ... + a_{n} X_{n} + ε$ (1)

式(1)中, a₀为常数项, a₁, a₂, a₃, ..., a_n为每个自变量对应的系数, ε 为回归方程的随机误差。

实际应用发现, 并不是自变量个数越多, 回归模型的精度越高, 在将一些与因变量相关性较低的自变量引入后, 回归模型的精度反而会降低。同时当自变量之间存在自相关的情况时, 简单的多元线性回归模型会出现多重共线性问题, 影响构建模型的准确性。

为了解决以上问题, 采用逐步回归的方法。多元逐步回归方法的因子挑选是逐个进行的, 首先通过相关性分析找出与因变量相关性最大的自变量因子, 建立最简单的线性回归方程, 并在每一步引入一个自变量进行F检验, 若通过检验则引入该自变量, 否则剔除。重复以上步骤, 直到变量子集中没有可进入或剔除的变量时, 回归过程停止。

使用Python软件进行多元逐步回归分析, 建立因变量与自变量的多元线性回归模型。按照分析结果最终保留了郁闭度、海拔、坡度、 Band5/Band4、 Band7/Band4、 Homogeneity_B1、 Entropy_B1、 SecondMoment_B1、 Correlation_B1。综合特征的回归模型方程为

$Y = - 835.523 + 751.527 X_{1} + 0.368 X_{2} + 1.904 X_{3} - 1.928 X_{4} + 8.829 X_{5} - 2326.276 X_{6} + 382.012 X_{7} + 1566.208 X_{8} - 58.810 X_{9}$ (2)

式(2)中, Y为蓄积量, X₁, X₂, ..., X₉依次为郁闭度、海拔、坡度、 Band5/Band4、 Band7/Band4、 Homogeneity_B1、 Entropy_B1、 SecondMoment_B1、 Correlation_B1。

1.6 基于BP神经网络的森林蓄积量反演

人工神经网络是以生物神经网络为基础来进行发展的, 其中最成熟和受到广泛应用的是采用误差反向传播算法(error back-propagation algorithm)的多层感知器, 也就是BP神经网络。其特点有: 分布式信息管理; 大规模并行处理; 自学习能力; 鲁棒性和容错性。

BP算法获得梯度的核心概念为局部梯度

$δ^{(i)} = \frac{\partial L (x)}{\partial u^{(i)}}$ (3)

式(3)中, L(x)为损失函数, u⁽ⁱ⁾为第i层的输入。

计算损失函数的梯度

$δ^{(m)} = \frac{\partial L (y, v^{(m)})}{\partial v^{(m)}} ϕ'_{m} (u^{(m)})$ (4)

式(4)中, y为空间中的向量, v⁽^m⁾为第m层的输出, v⁽^m⁾=ϕ _m(u⁽^m⁾)。

局部梯度的反向传播过程

$δ^{(i)} = δ^{(i + j)} \times W^{(i) T} ϕ'_{i} (u^{(i)})$ (5)

式(5)中, W⁽ⁱ⁾为第i层到下一层的权值矩阵^[12]。

使用Python软件对筛选出的10个自变量和1个因变量建立BP神经网络模型。

1.7 基于随机森林的森林蓄积量反演

随机森林(random forests)是基于决策树的机器学习方法, 其特点是利用有放回的抽样方法(Bootstrap)从样本数据中抽取n个数据作为训练集, 并基于这些数据构建CRAT分类树。由于在数据的选取上具有随机性和决策树数量参数的可调节性, 随机森林回归模型有明显的抗过拟合的特点, 因此在处理分类和回归的任务上, 该模型有良好的表现。随机森林(random forests)作为目前预测效果最好的非参数回归模型之一, 与参数回归方法相比, 该算法无需对变量的正态性和独立性等假设条件进行检验, 同时也不需要考虑多变量的共线问题。

基尼指数在随机森林回归中可以用来计算各特征在模型中的重要性, 其计算公式为

$Gin i_{m} = \overset{| K |}{\sum_{k = 1}} \overset{m}{\sum_{k' \neq k}} P_{mk} P_{mk'} = 1 - \overset{| K |}{\sum_{k = 1}} P_{mk}^{2}$ (6)

式(6)中, K为类别数, P_mk表示第m个节点中k所占比例。

特征x_j在第m个节点的Gini变化量计算公式为

$\begin{array}{l} V_{jm}^{Gini} = \overset{n}{\sum_{i = 1}} V_{ij}^{Gini} \\ (V_{jm}^{Gini} = Gin i_{m} - Gin i_{L} - Gin i_{R}) \end{array}$ (7)

式(7)中, Gini_L和Gini_R分别为第m个节点前后的Gini指数, 将所有特征的基尼指数做归一化处理即可得到各特征的重要性。

使用Python软件对上述筛选出的10个自变量和1个因变量建立随机森林回归模型(random forest regression model)。

2 结果与讨论

以森林蓄积量作为因变量, 多源特征为自变量, 根据各自变量与森林蓄积量之间的相关关系, 选择最优因子构建基于多源特征的森林蓄积量反演模型。为验证不同模型对森林蓄积量反演的精度高低, 采用多元线性逐步回归法、 BP神经网络和随机森林回归三种方法分别建立模型, 根据实际数据来设置相应的模型参数, 以达到每个模型的最优精度。

决定系数R²能够反映因变量y的总变异中可由回归模型中自变量解释的部分所占的比例, 用来衡量所建立模型效果的好坏。其取值范围为0≤ R²≤ 1, 决定系数越接近1, 表示样本数据对所选用的线性回归模型拟合越好^[13]。平均绝对误差MAE表示实际值与预测值之间绝对误差的平均值, 可以避免误差正负相抵的问题。均方根误差RMSE是实际值与观测值偏差的平方和与样本数比值的平方根, 常用作对模型精度进行评价的指标。选取可决系数(R²)、平均绝对误差(MAE)和均方根误差、 (RMSE)作为比较三种模型精度的指标。 R², MAE和RMSE的计算公式分别为

$R^{2} = 1 - \frac{\sum (y_{i} - {\hat{y}}_{i})}{\sum (y_{i} {- \hat{y})}^{2}}$ (8)

$MAE = \frac{1}{n} \overset{n}{\sum_{i = 1}} | y_{i} - {\hat{y}}_{i} |$ (9)

$RMSE = \sqrt[]{\frac{\overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i})^{2}}{n}}$ (10)

式(8)— 式(10)中: ${\hat{y}}_{i}$ 为像元蓄积量的预测值, y_i为像元蓄积量的实际值, $\hat{y}$ 为像元蓄积量的平均值。

2.1 不同反演模型的精度对比与分析

为了验证不同特征对模型精度的贡献, 本研究以单波段信息和样地数据为基础, 设置了3种不同的特征组合。通过上述步骤建立模型, 得到的R², MAE和RMSE如表1。

表1 建模结果 Table 1 Modeling result

结果显示地形、波段和纹理特征的组合精度最高, 其中随机森林回归模型(R²=0.739, MAE=55.352 m³· ha^-1, RMSE=63.195 m³· ha^-1)的精度优于多元逐步回归模型(R²=0.541, MAE=58.317 m³· ha^-1, RMSE=71.562 m³· ha^-1)和BP神经网络模型(R²=0.477, MAE=67.503 m³· ha^-1, RMSE=73.226 m³· ha^-1)。表明在多特征的森林蓄积量反演研究中, 随机森林回归模型的估测效果最好, 这是由随机森林回归擅长处理高维度数据和抗过拟合等特点决定的。

在加入波段比值后, 多元逐步回归的R²提升了0.039, MAE和RMSE分别下降了3.68和3.386 m³· ha^-1。 BP神经网络的R²提升了0.034, MAE和RMSE分别下降了0.755和4.638 m³· ha^-1。随机森林回归的R²提升了0.035, MAE和RMSE分别下降了3.511和4.517 m³· ha^-1。加入纹理特征后, 多元逐步回归的R²提升了0.105, MAE和RMSE分别下降了10.408和6.45 m³· ha^-1。 BP神经网络的R²提升了0.08, MAE和RMSE分别下降了2.666和6.777 m³· ha^-1。随机森林回归的R²提升了0.122, MAE和RMSE分别下降了8.523和9.262 m³· ha^-1。这说明波段比值和纹理特征的参与可以有效提升预测模型的精度。

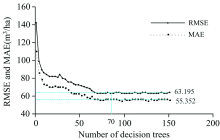
实验发现随机森林回归模型的决策树数量设置为70时, 模型的平均绝对误差MAE和均方根误差RMSE逐渐趋于平稳, 且运算速度较更多决策树时更快。运算过程如图2。

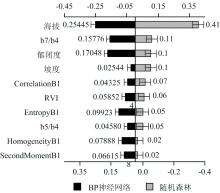
	Figure Option View Download New Window
	图2 决策树数量与RMSE, MAE的关系Fig.2 Relationship of the number of decision trees and the error

根据测试结果可知, 海拔在BP神经网络和随机森林回归中的贡献率均为最高, 分别是25%和41%。各特征重要性如图3。

	Figure Option View Download New Window
	图3 各特征的重要性Fig.3 The importance of each feature

3种模型对森林蓄积量都有一定的预测能力, 其中随机森林模型的散点分布更集中, R²为0.739, 说明随机森林模型在本研究中预测能力更强。本次蓄积量反演预测值的范围为121.3~372.8 m³· ha^-1, 森林资源二类调查数据的实测值为50.7~482.9 m³· ha^-1, 结果显示在蓄积量较小时预测值偏大, 蓄积量较大时预测值偏小, 该现象表明在蓄积量的预测中波段值的饱和现象不能完全消除。 3种模型的预测散点图如图4。

	Figure Option View Download New Window
	图4 不同反演模型的散点图Fig.4 Scatter plots of different inversion models

2.2 模型精度的比较

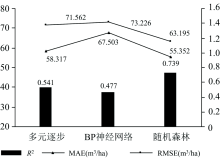
由表1可知, 三种模型中拟合效果最好的是随机森林模型, R²为0.739; 随机森林模型的MAE和RMSE均为最低, 分别是55.352和63.195 m³· ha^-1。三种模型的R², MAE和RMSE的比较如图5。

	Figure Option View Download New Window
	图5 精度比较Fig.5 Comparison of accuracy

3 结论

以Landsat OLI遥感卫星的影像数据、 DEM数据和森林资源二类调查数据为基础, 选择西藏自治区林抓市米林县全县的林地区域为研究区进行蓄积量的反演研究。

(1)基于多特征的蓄积量反演中, 随机森林模型的预测精度最高。

(2)合理选择建模变量的个数可以有效提升模型的精度与构建效率。

(3)纹理特征和波段比值参与建模可以有效提升建模精度。

本研究结果表明:

(1)高分辨率的影像数据具有更丰富的纹理信息, 可以有效提升模型的精度。本研究采用空间分辨率为30 m的Landsat OLI遥感影像数据, 模型精度R²达到了0.739。郝泷等^[1]利用Landsat OLI对西藏林芝市进行森林蓄积量的反演, 精度为0.708。菅永峰等^[2] 利用更高分辨率的GF-2和SPOT-6数据对太子山林场的森林蓄积量估测, 精度R²达到了0.88。蒙诗栎等^[14]利用WorldView-2对凉水自然保护区进行了蓄积量的反演, 精度R²为0.85。在此基础上, 曾伟生等^[3]和朱思名等^[4]利用机载雷达和无人机影像对蓄积量进行研究并取得了成功。因此选用先进的设备获取更高分辨率的影像建模在今后的研究中还可进一步探索。

(2) 研究区是位于西藏自治区东南部的米林县, 其气候为高原温带半湿润性季风气候, 海拔较高且降水较多, 该地区的气候属性和地理特征具有明显的特点。竹万宽等^[15]认为海拔影响植被的生长环境, 在蓄积量的反演中具有重要作用, 与本工作的建模变量重要性结果一致。气温、光照、降水等对植物的地上部分生长具有显著影响, 因此对气候条件和地理特征区别较大地区的蓄积量反演需要根据实际情况, 对变量因子和模型参数进行合理的选取与设置。

(3)研究结果显示, 波段比值和纹理特征参与建模后, 随机森林模型精度R²分别提升了0.035和 0.122。蓄积量反演预测值的范围为121.3~372.8 m³· ha^-1, 森林资源二类调查数据的实测值为50.7~482.9 m³· ha^-1, 在蓄积量较小时预测值偏大, 蓄积量较大时预测值偏小, 表明在蓄积量的预测中波段值的饱和现象不能完全消除, 与菅永峰等^[2]对波段饱和现象的研究结论一致。为了降低饱和现象对蓄积量预测的影响, 可加入具有更丰富信息的纹理特征和贡献率更高的波段比值来提升模型的精度, 以期在实际预测中效果更佳。

参考文献

文献列表

[1]	HAO Shuang, LIU Hua, CHEN Yong-fu, et al(郝泷, 刘华, 陈永富, 等). Mountain Research(山地学报), 2017, 35(2): 246. [本文引用:3]
[2]	JIAN Yong-feng, HAN Ze-min, HUANG Guang-ti, et al(菅永峰, 韩泽民, 黄光体, 等). Acta Ecologica Sinica(生态学报), 2021, 41(6): 2161. [本文引用:4]
[3]	ZENG Wei-sheng, SUN Xiang-nan, WANG Liu-ru, et al(曾伟生, 孙乡楠, 王六如, 等). Scientia Silvae Sinicae(林业科学), 2021, 57(2): 31. [本文引用:2]
[4]	ZHU Si-ming, WANG Zhen-xi, PEI Yuan, et al(朱思名, 王振锡, 裴媛, 等). Journal of Arid Land Resources and Environment(干旱区资源与环境), 2020, 34(10): 160. [本文引用:2]
[5]	YANG Liu, FENG Zhong-ke, YUE De-peng, et al(杨柳, 冯仲科, 岳德鹏, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(7): 2140. [本文引用:1]
[6]	Obata S, Cieszewski C J, Lowe R C, et al. Remote Sensing, 2021, 13(2): 218. [本文引用:1]
[7]	Mauya E W, Koskinen J, Tegel K, et al. Forests, 2019, 10(3): 279. [本文引用:1]
[8]	ZHOU Jun-hong, WANG Zi-zhi, LIAO Sheng-xi, et al(周俊宏, 王子芝, 廖声熙, 等). Transactions of the Chinese Society for Agricultural Engineering(农业工程学报), 2021, 37(4): 216. [本文引用:1]
[9]	JIANG Fu-gen, SUN Hua, ZHAO Feng, et al(蒋馥根, 孙华, ZHAO Feng, 等). Journal of Forest and Environment(森林与环境学报), 2019, 39(5): 497. [本文引用:1]
[10]	TANG Yu, SHI Tie-mao, BU Ying-jie, et al(汤煜, 石铁矛, 卜英杰, 等). Chinese Journal of Ecology(生态学杂志), 2020, 39(4): 1387. [本文引用:1]
[11]	CHENG Wen-sheng, FENG Zhong-ke, YU Jing-xin(程文生, 冯仲科, 于景鑫). Transactions of The Chinese Society for Agricultural Machinery(农业机械学报), 2017, 48(3): 245. [本文引用:1]
[12]	LI Xu-qing, LI Long, ZHUANG Lian-ying, et al(李旭青, 李龙, 庄连英, 等). Transactions of The Chinese Society for Agricultural Machinery(农业机械学报), 2019, 50(6): 226. [本文引用:1]
[13]	LIU Yan-jun, XIA Kai, FENG Hai-lin, et al(刘彦君, 夏凯, 冯海林, 等). Acta Scientiae Circumstantiae(环境科学学报), 2019, 39(4): 1241. [本文引用:1]
[14]	MENG Shi-li, PANG Yong, ZHANG Zhong-jun, et al(蒙诗栎, 庞勇, 张钟军, 等). Journal of Remote Sensing(遥感学报), 2017, 21(5): 812. [本文引用:1]
[15]	ZHU Wan-kuan, XU Yu-xing, WANG Zhi-chao, et al(竹万宽, 许宇星, 王志超, 等). Scientia Silvae Sinicae(林业科学), 2020, 56(5): 1. [本文引用:1]

2017

0.0

... 例如郝泷等^[1]利用Landsat OLI影像估算了西藏林芝市的森林蓄积量, 菅永峰等^[2]以GF-2和SPOT-6数据为基础对湖北省太子山林场的森林蓄积量进行了研究, 曾伟生等^[3]利用机载激光雷达数据建立了东北林场的森林蓄积量估算模型, 朱思名等^[4]利用无人机影像对天山云杉林蓄积量进行了研究 ...

... 例如郝泷等^[1]研究了地形因子和纹理特征对蓄积量反演的影响, 杨柳等^[5]估算了不同树种的蓄积量, 该方法的综合精度高于传统的实地测量, 且更适合于广泛应用 ...

... 郝泷等^[1]利用Landsat OLI对西藏林芝市进行森林蓄积量的反演, 精度为0 ...

2021

0.0

... 例如Ernest William Mauya等^[7]用多元线性回归估测了坦桑尼亚小规模人工林的蓄积量, 周俊宏等^[8]利用神经网络算法对普达措国家公园进行了遥感估算, 菅永峰等^[2]使用随机森林回归模型估测了湖北省太子山林场的森林蓄积量, 蒋馥根等^[9]利用KNN方法估测了旺业甸林场的森林蓄积量, 张超等利用偏最小二乘回归法估测了三峡水库区域的蓄积量 ...

... 菅永峰等^[2] 利用更高分辨率的GF-2和SPOT-6数据对太子山林场的森林蓄积量估测, 精度R²达到了0 ...

... ha^-1, 在蓄积量较小时预测值偏大, 蓄积量较大时预测值偏小, 表明在蓄积量的预测中波段值的饱和现象不能完全消除, 与菅永峰等^[2]对波段饱和现象的研究结论一致 ...

2021

0.0

... 在此基础上, 曾伟生等^[3]和朱思名等^[4]利用机载雷达和无人机影像对蓄积量进行研究并取得了成功 ...

2020

0.0

... 在此基础上, 曾伟生等^[3]和朱思名等^[4]利用机载雷达和无人机影像对蓄积量进行研究并取得了成功 ...

2017

0.0

2021

0.0

... 随机森林模型有着抗过拟合和擅长处理高维度数据的优点, 但运行速度较其他方法慢, 且需要根据不同的数据设置不同的参数^[6] ...

2019

0.0

2021

0.0

2019

0.0

2020

0.0

... 本研究以西藏林芝市米林县为研究区域, 以Landsat OLI的多光谱数据、 DEM数据和森林资源二类调查数据为基础^[10], 采用多元线性逐步回归法、 BP神经网络和随机森林回归三种方法分别建立模型, 根据实际数据来设置相应的模型参数, 以达到每个模型的最优精度 ...

2017

0.0

... 研究区主要由针叶林、阔叶林、针阔混交林组成, 利用二元材积表^[11]对样地的蓄积量进行计算 ...

2019

0.0

... 式(5)中, W⁽ⁱ⁾为第i层到下一层的权值矩阵^[12] ...

2019

0.0

... 1, 决定系数越接近1, 表示样本数据对所选用的线性回归模型拟合越好^[13] ...

2017

0.0

... 蒙诗栎等^[14]利用WorldView-2对凉水自然保护区进行了蓄积量的反演, 精度R²为0 ...

2020

0.0

... 竹万宽等^[15]认为海拔影响植被的生长环境, 在蓄积量的反演中具有重要作用, 与本工作的建模变量重要性结果一致 ...