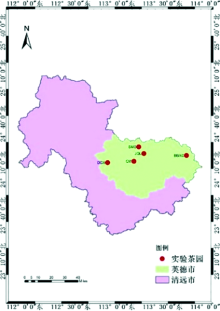
实验区位于广东省清远市英德市积庆里、 创美、 德高信、 八百秀才和石门山5个茶园(图1), 该区域位于北纬24.50° , 东经113.55° , 平均海拔为181 m, 地处南亚热带向中亚热带的过渡地区, 属亚热带季风气候。 茶鲜叶光谱数据采集在2020年5月、 7月和9月开展, 覆盖3个品种(包括主栽品种英红九号, 鸿雁十二号, 金萱), 采样点均匀分布于实验区内, 共选取了151个样本点, 每个样点采集茶鲜叶样品约200 g, 进行化验。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区域空间分布Fig.1 Spatial distribution of study area

叶片的光谱反射率采用美国ASD Fieldspec Pro3光谱仪测量, 其波谱覆盖范围为350~2 500 nm, 光谱重采样间隔为1 nm。 利用叶片夹持器(自带光源)选取叶片的中部较宽的部分进行光谱测定, 手柄中的光源部分直接夹紧茶叶叶片所测部位, 叶片夹持器测定使叶片处于密闭条件下, 且所测面积相同, 保证光谱数据获取的精确性和稳定性。 取10片标准叶片在相同样点采集光谱数据, 10个光谱反射率的平均值作为该样点叶片的光谱反射率。

采集光谱数据后的茶鲜叶放于120 ℃烘箱中杀青固样30 min, 然后置于80~90 ℃下烘至足干。 干燥后的样品磨碎后参照GB5009.5— 2016, 通过凯氏定氮法测量其全氮量。

1.3.1 常规光谱预处理方法

采用卷积平滑(SG)、 去趋势(Detrending)、 一阶导数(1st)、 多元散射校正(MSC)和标准正态变量变换(SNV)五种预处理方法, 对原始光谱数据进行预处理作为参考。

1.3.2 小波变换

连续小波变换(CWT)起源于傅里叶变换信号处理技术, 同时开展频率和时间分析, 从复杂的原始光谱信号中分辨细微的变换, 捕捉有益信息, 表征光谱局部特征信息。 小波变换分析广泛应用于高光谱数据的降维压缩、 噪声去除、 特征选择以及弱信号提取等方面。 小波分析包括连续分解与离散分解两种类型的小波变换, Wang等^[11]研究表明离散小波随着分解尺度的增加, 光谱维度减半, 不能对光谱数据进行较好的分析。 连续小波变换是一种连续分解信号的方法, 其输出光谱可以与原始光谱直接进行对比, 比离散小波变换后获得的光谱更易于解释。 通过以式(1)缩放和移动小波母函数

Ψa, b=1aΨλ-ba(1)

式(1)中, λ 为茶叶叶片高光谱数据的波段数, a和b分别代表伸缩因子(即宽度)和平移因子(即位置), 这两个变量都为正实数。 CWT的输出公式如式(2)

Wf(a, b)=(f, Ψa, b)=∫-∞+∞f(λ)Ψa, b(λ)dλ(2)

式(2)中, f(λ )为高光谱反射率, CWT系数(W_f(a_i, b_j), i=1, 2, ..., m; j=1, 2, ..., n)包含两维(即m× n矩阵), 其中一维为波长(1, 2, ..., n), 另一维是分解尺度(1, 2, ..., m), 因此, 小波系数是一个行为尺度, 列为波长的矩阵。

由于Mexh小波在高光谱分解方面表现出色^[12], 且光谱吸收特性与高斯函数相似, 因此选取Mexh作为小波母函数, 使用连续小波分析(continuous wavelet transformation, CWT)以执行尺度2¹~2¹⁰分解反射光谱为10个尺度, 并获取不同分解尺度下的不同波长的一系列小波系数, 进行了小波系数与茶叶N素含量的相关性分析, 并用于构建校准模型。

1.3.3 特征变量选择方法

连续投影(SPA)是一种前向变量选择方法, 使用简单的投影操作来获得具有最小共线性的变量子集, 并可以根据交叉验证的最小均方根误差(RMSE)选择最终的最佳波长。

竞争性自适应重加权采样(CARS)结合蒙特卡洛采样和PLSR, 基于达尔文进化论, 遵循“ 适者生存” 的原则, 根据每个变量的重要性, 以迭代和竞争的方式从N个蒙特卡洛采样顺序中选择N个变量子集。

变量组合集群分析(variable combination population analysis, VCPA)是一种新的有效的变量选择方法, 它由Yun等建立^[13]。 VCPA的实现过程分为两个基本步骤, 首先基于“ 适者生存” 原理的指数递减函数(exponentially decreasing function, EDF)选择有用的变量并缩小变量空间, 其次通过二进制矩阵采样(binary matrix sampling, BMS)选择最佳光谱波长子集, 通过生成随机变量组合, 确保每个变量都有机会被选择并产生各种变量子集, 在每个EDF和BMS运行的周期中都采用模型集群分析(model population analysis, MPA)根据较低的RMSECV来确定最优变量子集。 分别利用SPA, CARS和VCPA对连续小波变换处理后的光谱数据进行进一步的特征波段提取。

经过连续小波变换后的光谱, 通过SPA、 CARS和VCPA方法进行变量筛选, 利用偏最小二乘法(partial least squaresreg ression, PLSR)构建茶鲜叶N含量的估测模型。 采用Kennard-Stone(KS)方法以近似3:1比例选取113个样本数据作为建模集, 用于构建估测模型, 剩余的38个样本数据作为验证集, 用于预测模型精度和稳定性的验证。 模型精度采用模型评价参数决定系数(R²)与均方根误差(RMSE)来综合评价模型表现, 其计算方法如式(3)和式(4)

R2=1-∑i=1n(YI-Y'I)2∑i=1n(YI-Y^I)2(3)

RMSE=∑i=1n(YI-Y'I)2n(4)

式(3)和式(4)中, n为样本个数, i为样本, Y_I和Y'_I分别是样品的实测与预测值, Y^为实测样品平均值。

使用Matlab R2018b(The Math Works, Natick, USA)、 Unscrambler X10.4(CAMO AS, Oslo, Norway)、 SPSS 26(IBM, USA)、 Origin 2019b(OriginLab, USA)等软件。

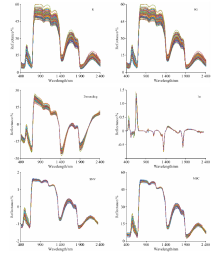
图2展示了5种预处理后的高光谱。 与原始光谱(R)相比, 预处理1st和Detrending方法明显改变了光谱特性, 在具体波段上凸显了光谱信息, 而SG, MSC和SNV预处理方法没有明显改变光谱吸收特性, 光谱特征变化幅度小, 与原始光谱相比更加平滑与集中。 上述5种预处理算法有效地平滑光谱曲线, 且可以保留光谱信息的有用信息。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同预处理方法下光谱反射率Fig.2 Reflectance spectra with different pre-processing methods

2.2.1 基于小波变换的光谱分析

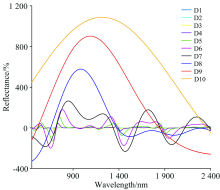
原始光谱经CWT处理后的结果如图3所示, D1— D10分别代表了以2¹— 2¹⁰为分解尺度经过CWT分解得到的10层小波能量系数模拟光谱分辨率。 可以看出, 1— 7尺度上的光谱分辨率, 随着分解层数的增加, 光谱吸收、 反射波谱特征均加强, 光谱波动范围加大, 8— 10尺度的光谱反射率起伏变化较大。 总体来看, 随着CWT分解尺度的不断增加, 原始光谱反射率的波峰特征(761, 1 070, 1 217和1 645 nm)与波谷特征(670, 902, 1 447和1 931 nm)被不断放大, 并且均有一定的红移与蓝移现象。 小尺度分解可以较好的保持原始光谱特性, 随着分解层数的增加, 光谱特征在不断凸显的过程中也不断被拉伸, 在大尺度分解中又可以凸显具体波段的细微特征信息。 这是因为CWT是基于光谱曲线的形状特征, 捕获光谱形状的差异并凸显特征^[14], 更有利于捕捉原始光谱反射率的微弱变化, 有利于进行N含量对茶叶鲜光谱响应特征的分析。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 小波变换光谱特性Fig.3 Spectral characteristics of wavelet transform

2.2.2 相关性分析

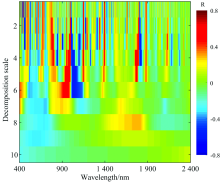
小波系数能量与N素实测数据进行相关性分析, 如图4所示。 可看出各尺度小波系数与茶鲜叶N含量的相关系数差异较大, 且随着分解尺度的增加呈逐渐集中分布的趋势。 由图可知, 相关性较高的波段表现为更明显的红色区域, 相关系数较大的波长主要与N素、 叶绿素以及类胡萝卜素等物质的复杂性有关, 对于选定的493, 987, 1 193, 1 195和1 825 nm, 这些波段大多为N素的重要光谱区域^[15], 另外可以看出, 小波变换后的光谱在小尺度分解下与茶鲜叶N素存在良好的相关性, 选取1— 6尺度作进一步分析。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 小波变换相关性分析Fig.4 Correlation analysis of wavelet transform

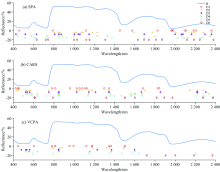
为了比较不同变量筛选方法对茶鲜叶N含量高定量模型的影响, 将经过CWT处理的光谱数据分别利用SPA, CARS和VCPA进行变量筛选。 SPA设置选择的最小和最大变量数的参数分别为1和30, 分别对CWT处理后的小波系数进行光谱特征变量的选取, 结果如图5(a)所示, 光谱变量分别减少到15, 16, 17, 11, 14和18个。 CARS设置蒙特卡洛抽样运行次数为50, 十倍交叉验证用于评估每个子集的效用, 分别对CWT处理后的小波系数进行光谱特征变量的选取。 结果如图5(b)所示, 光谱变量分别减少到16, 19, 17, 16, 15和17个。 VCPA设置EDF剩余变量数为100, 迭代次数为50, 最优子模型的比例为10%, BMS运行次数为1 000, VCPA步骤中每个BMS采样的平均数设置为20, 并采用5折交叉验证分别对CWT处理后的小波系数进行光谱特征变量的选取, 结果如图5(c)所示。 可以看出基于CWT小波分解后的光谱数据通过VCPA的五次迭代将全波段光谱变量分别减少到12, 11, 10, 11, 8和8个。 相比SPA和CARS, VCPA选择的变量更少, 这表明该方法在数据降维方面有着巨大的优势。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 SPA, CARS和VCPA筛选的特征变量Fig.5 The variables selected by SPA, CARS and VCPA

2.4.1 基于常规预处理方法和特征筛选的N素含量预测

采用卷积平滑(SG)、 去趋势(Detrending)、 一阶导数(1st)、 多元散射校正(MSC)和标准正态变量变换(SNV)5种传统光谱处理技术分析茶鲜叶光谱特性, 并采用偏最小二乘算法建立茶鲜叶N素含量预测模型作为参考, 结果如表1所示。

表1

Table 1

表1(Table 1)

表1 基于不同预处理方法和变量选择方法的模型 Table 1 Models based on different preprocessing methods and variables selection methods 模型 光谱处理 主成分 建模集 预测集 RC2 RMSEC RP2 RMSEP SG 8 0.50 0.42 0.37 0.48 Detrending 9 0.59 0.35 0.58 0.38 SPA-PLSR 1st 7 0.63 0.37 0.61 0.35 SNV 10 0.71 0.31 0.60 0.39 MSC 8 0.62 0.38 0.68 0.29 SG 5 0.62 0.35 0.55 0.41 Detrending 10 0.75 0.30 0.71 0.29 CARS-PLSR 1st 11 0.79 0.26 0.73 0.32 SNV 11 0.71 0.33 0.68 0.29 MSC 11 0.73 0.29 0.62 0.39 SG 6 0.81 0.24 0.65 0.37 Detrending 10 0.83 0.25 0.73 0.31 VCPA-PLSR 1st 9 0.86 0.18 0.84 0.25 SNV 7 0.81 0.25 0.67 0.35 MSC 6 0.82 0.24 0.72 0.32

表1 基于不同预处理方法和变量选择方法的模型 Table 1 Models based on different preprocessing methods and variables selection methods

2.4.2 基于小波变换和特征筛选的N素含量预测

使用CWT处理后的光谱数据筛选后的特征波段作为自变量, 以茶鲜叶N含量为因变量, 采用偏最小二乘法构建茶鲜叶N含量的估测模型(表2)。 由表2可知, 经过CWT处理后光谱构建的模型均表现出较好的拟合精度, 并且随着分解尺度的增加模型精度呈现下降趋势, 说明小规模分解通常能够改善CWT处理后的小波系数对分析物的敏感性, 这与Liu等的研究结果一致^[16]。 其中SPA选择变量估测茶鲜叶N含量的精度较低, 1— 6尺度建模R²范围在0.65~0.83, RMSE范围在0.25~0.33, 预测R²范围在0.65~0.83, RMSE范围在0.25~0.33; 以CARS选择变量为因变量, 1— 6尺度建模R²范围在0.73~0.91, RMSE范围在0.19~0.32, 预测R²范围在0.64~0.88, RMSE范围在0.24~0.35; VCPA选择变量估测模型表现最好, 1— 6尺度建模R²范围在0.73~0.95, RMSE范围在0.16~0.29, 预测R²范围在0.73~0.90, RMSE范围在0.23~0.35, 其中在1尺度下的模型拟合效果最高。

表2

Table 2

表2(Table 2)

表2 基于不同分解层数和变量选择方法的模型 Table 2 Models based on different decomposition scales and variables selection methods 模型 分解尺度 主成分 建模集 预测集 RC2 RMSEC RP2 RMSEP SPA-PLSR 1 5 0.83 0.25 0.72 0.37 2 7 0.72 0.30 0.68 0.36 3 10 0.74 0.31 0.69 0.33 4 11 0.78 0.28 0.67 0.35 5 11 0.79 0.26 0.60 0.41 6 11 0.65 0.33 0.60 0.42 CARS-PLSR 1 7 0.91 0.19 0.88 0.24 2 8 0.81 0.24 0.76 0.32 3 12 0.81 0.25 0.73 0.31 4 8 0.82 0.26 0.69 0.29 5 10 0.78 0.28 0.64 0.35 6 11 0.73 0.32 0.68 0.32 VCPA-PLSR 1 7 0.95 0.16 0.90 0.23 2 7 0.83 0.23 0.82 0.27 3 10 0.81 0.26 0.79 0.26 4 8 0.82 0.24 0.73 0.30 5 8 0.81 0.25 0.77 0.30 6 7 0.73 0.29 0.74 0.35

表2 基于不同分解层数和变量选择方法的模型 Table 2 Models based on different decomposition scales and variables selection methods

图6所示为不同变量选择方法下最优估测模型实验值与预测值1:1对比图, 可以看出CWT-VCPA模型表现最优, 训练集和验证集的R²分别为0.95和0.90, RMSE分别为0.16和0.23, 二者差异较小, 相比于CWT-SPA和CWT-CARS, 建模及预测集的预测精度最高。 对比各模型可知, CWT方法结合特征变量选择算法明显提升了模型的精度, 且CWT-VCPA筛选变量估算N含量效果最好。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 基于(a)CWT(1尺度)-SPA-PLSR, (b)CWT(1尺度)-CARS-PLSR和(c)CWT(1尺度)-VCPA-PLSR的氮含量最佳模型的拟合1:1拟合图Fig.6 Fitting diagrams of the optimal models of tea nitrogen based on (a) CWT (1 scale)-SPA-PLS, (b) CWT (1 scale)-CARS-PLS and (c) CWT (1 scale)-VCPA-PLS

以茶鲜叶为研究对象, 构建并对比分析了常用5种光谱处理与连续小波分解方法的N含量估测模型。 研究结果表明, 与常规光谱处理方法相比, 小波变换方法可明显提升茶鲜叶光谱对N含量的响应, 且模型精度与稳定性均较高。 这是由于在常规的光谱预处理方法中, SNV, MSC和Detrending通常用于校正低频散射信号、 1st可以消除信号的基线漂移, 而CWT可以同时消除光谱信号中的高频和低频噪声, 并且连续小波分解本质上是一种基于相关性的方法, 可以捕获对茶多酚含量最敏感的小波特征, 这种频谱相关性的方法在凸显光谱细微变化特征方面效果显著, 更有利于后续对光谱特征波段的提取。 随着分解尺度的增加, 模型预测精度逐步降低, 主要原因是光谱中含有较多的噪声, 造成了光谱的有益信息与噪声的分布波段区间有较高的重叠性, 且随着CWT分解尺度的增加, 其内含的有益信息与无益噪声信息重新分配, 导致引入的噪声信息较多从而降低模型的预测精度。 在1— 6尺度模型精度达到最低时相较于传统光谱变换仍然有一定程度的提升, 表明CWT能提取光谱特征中的有益信息, 并一定程度上分离无用噪声, 提升光谱信息信噪比。 基于三种不同波段筛选方法(SPA, CARS和VCPA)都可以在减少变量的同时提升模型预测效果, 且相比于SPA和CARS, VCPA选择的变量更少, 预测效果更好。 这归因于EDF对变量的连续收缩, 在EDF的每次运行中, 都会消除一些贡献较小的变量。 此外, 还与BMS和MPA的使用有关, BMS是一种采样策略, 它为所有变量提供了相同的机会进行采样, 使用不同的变量组合用于子模型的构建。 MPA用于提取子模型中包含的最佳变量组合, 比较每个子模型的RMSECV, 保留最佳10%子模型中具有最高频率的变量^[17]。 因此, VCPA通过最少的选择变量, 保证了光谱数据集更好的可预测性。 当将最佳波长与全光谱进行比较时, 基于CWT分解光谱结合VCPA筛选特征变量的PLSR模型比其他光谱变换的PLSR模型具有更高的性能(R²=0.95), 并且减少了全光谱数据变量的99.34%, 极大的简化了建模过程。 综上可知, CWT-VCPA方法在实现对茶鲜叶N含量的定量监测方面具有强大的潜力。